Similar presentations:
Funkcje (Analiza matematyczna 1, wykład 2)
1. Slajd 1
FUNKCJE(Analiza Matematyczna 1, wykład 2)
Analiza Matematyczna 1, Wykład 2
1
2. Slajd 2
X ,Y - niepuste zbiory.Funkcja (odwzorowanie, przekształcenie)
f : X Y
przyporządkowuje, każdemu elementowi zbioru X dokładnie jeden element
zbioru Y .
Zbiór X jest dziedziną, a Y zbiorem wartości funkcji f .
Jeżeli y0 f ( x0 ) , to x0 jest argumentem, a y0 wartością funkcji f w punkcie x0 .
X
Y
funkcja
X
Y
funkcja „na”
X
Y
nie jest funkcją
Jeżeli f ( x0 ) 0, to x0 jest miejscem zerowym funkcji f .
Uwaga.
Wykład jest poświęcony funkcją rzeczywistym zmiennej rzeczywistej, tj.
f : X Y , gdzie X ,Y R.
Analiza Matematyczna 1, Wykład 2
2
3. Slajd 3
Wykresem funkcji f jest zbiór punktów płaszczyzny (podzbiórproduktu kartezjańskiego R R )
{( x, f ( x )) : x X } .
Funkcja f na zbiorze A jest:
10 rosnąca x1 , x2 A, ( x1 x2 f ( x1 ) f ( x2 ))
2 0 malejąca x1 , x2 A, ( x1 x2 f ( x1 ) f ( x2 ))
3 0 niemalejąca x1 , x2 A, ( x1 x2 f ( x1 ) f ( x2 ))
4 0 nierosnąca x1 , x2 A, ( x1 x2 f ( x1 ) f ( x2 ))
W szczególności funkcje rosnące albo malejące nazywamy ściśle
monotonicznymi.
Analiza Matematyczna 1, Wykład 2
3
4. Slajd 4
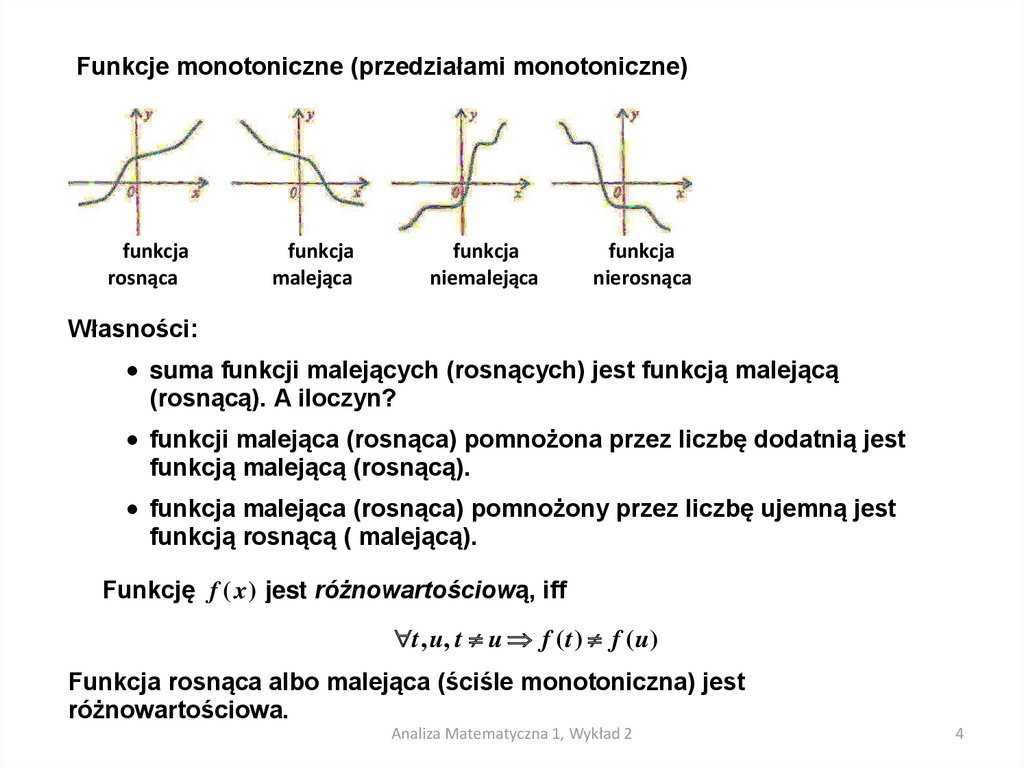
Funkcje monotoniczne (przedziałami monotoniczne)funkcja
rosnąca
funkcja
malejąca
funkcja
niemalejąca
funkcja
nierosnąca
Własności:
suma funkcji malejących (rosnących) jest funkcją malejącą
(rosnącą). A iloczyn?
funkcji malejąca (rosnąca) pomnożona przez liczbę dodatnią jest
funkcją malejącą (rosnącą).
funkcja malejąca (rosnąca) pomnożony przez liczbę ujemną jest
funkcją rosnącą ( malejącą).
Funkcję f ( x ) jest różnowartościową, iff
t , u, t u f (t ) f (u)
Funkcja rosnąca albo malejąca (ściśle monotoniczna) jest
różnowartościowa.
Analiza Matematyczna 1, Wykład 2
4
5. Slajd 5
Funkcja f na zbiorze A jest:10 parzystą x A, ( x A f ( x ) f ( x ))
2 0 nieparzystą x A, ( x A f ( x ) f ( x ))
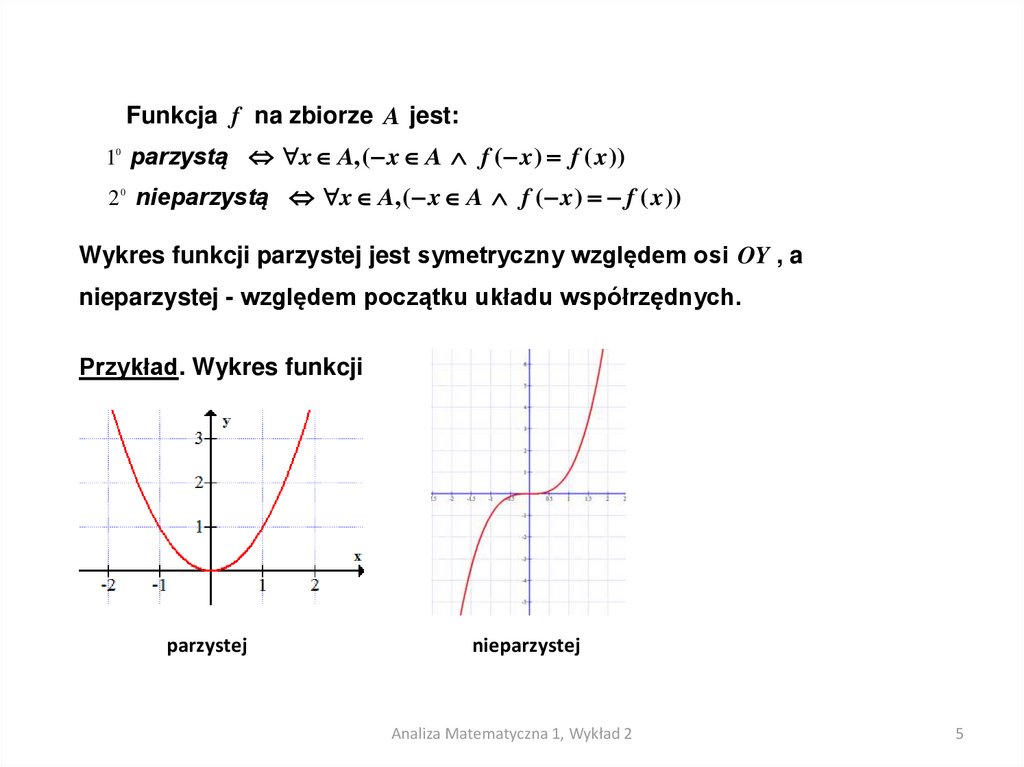
Wykres funkcji parzystej jest symetryczny względem osi OY , a
nieparzystej - względem początku układu współrzędnych.
Przykład. Wykres funkcji
parzystej
nieparzystej
Analiza Matematyczna 1, Wykład 2
5
6. Slajd 6
Przykład.a) y f ( x )
x
Dziedzina: X x R : x 0 [0, ), pierwiastek kwadratowy jest
określony tylko dla liczb dodatnich oraz zera.
Zbiór wartości Y [0, ).
Jest funkcją rosnącą oraz różnowartościową
Wobec tego f : X Y jest wzajemnie jednoznaczna (tj.
różnowartościowa i na), co zapisujemy
f : X Y .
1 1
Funkcja ta nie jest ani parzysta, ani nieparzysta.
Analiza Matematyczna 1, Wykład 2
6
7. Slajd 7
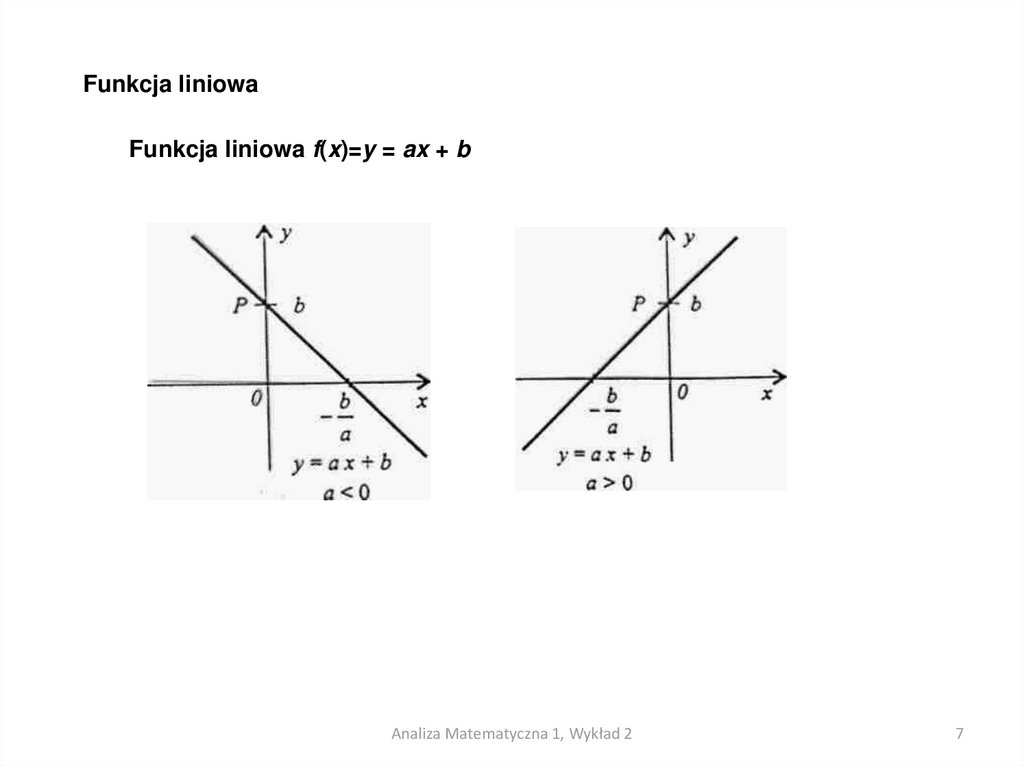
Funkcja liniowaFunkcja liniowa f(x)=y = ax + b
Analiza Matematyczna 1, Wykład 2
7
8. Slajd 8
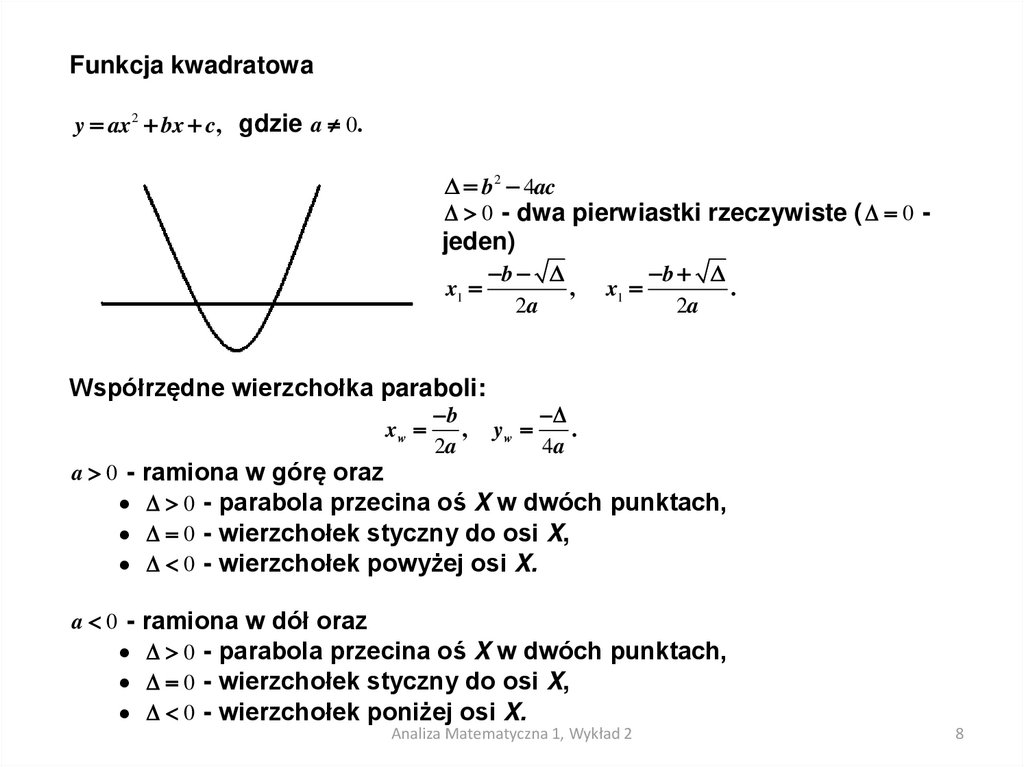
Funkcja kwadratoway ax 2 bx c, gdzie a 0.
b2 4ac
0 - dwa pierwiastki rzeczywiste ( 0 -
jeden)
x1
b
,
2a
Współrzędne wierzchołka paraboli:
xw
b
,
2a
yw
x1
b
.
2a
.
4a
a 0 - ramiona w górę oraz
0 - parabola przecina oś X w dwóch punktach,
0 - wierzchołek styczny do osi X,
0 - wierzchołek powyżej osi X.
a 0 - ramiona w dół oraz
0 - parabola przecina oś X w dwóch punktach,
0 - wierzchołek styczny do osi X,
0 - wierzchołek poniżej osi X.
Analiza Matematyczna 1, Wykład 2
8
9. Slajd 9
WielomianyWielomianem stopnia n jest funkcja postaci:
Wn(x) = anxn + ... + a1x + a0,
gdzie ai R, an 0.
Liczba a jest pierwiastkiem (zerem) wielomianu, jeżeli Wn(a) =0, tzn.
a a ... a a a 0
n
n
1
0
Przykład.
Liczba a = -1 jest pierwiastkiem wielomianu:
W(x) = 3x5 9x2 2x+10,
ponieważ W(-1) = 3(-1)5 9(-1)2 2(-1) + 10 = 0
Wyznaczanie miejsc zerowych wielomianów (algorytmy pierwiastkowe)
Algorytm Ferro, Tartaglii – wielomiany stopnia 3.
Algorytm Ferrari – wielomiany stopnia 4.
Twierdzenie Nielsa Abela i Evarista Galois – nie istnieje
algorytm pierwiastkowy dla wielomianów stopni n 5 .
Analiza Matematyczna 1, Wykład 2
9
10. Slajd 10
Funkcje wymierneFunkcja wymierna jest ilorazem dwóch wielomianów, tj.
w ( x)
f ( x)
,
g ( x)
n
m
gdzie w ( x ) i g ( x ) są wielomianami.
n
m
Dziedziną jest R oprócz miejsc zerowych wielomianu g ( x ) .
m
Analiza Matematyczna 1, Wykład 2
10
11. Slajd 11
Działania na funkcjach, składanieFunkcję
f : X Y ,
gdzie X R i Y R możemy traktować jako
f : X R.
Jeżeli
f : X R i g : X R,
to definiujemy ich sumę, iloczyn, iloraz, mnożenie przez stałą,
odpowiednio:
( f g )( x ) f ( x ) g( x ) , ( f g )( x ) f ( x ) g( x ) ,
f
f ( x)
( )( x )
g
g( x )
dla
g( x ) 0 oraz x X .
Analiza Matematyczna 1, Wykład 2
11
12. Slajd 12
Złożenie (superpozycja) funkcjiMając dwie funkcje f : X Y i g : Y Z , można utworzyć funkcję
złożoną,
( g f ) : X Z
określoną wzorem ( g f )( x ) g f ( x ) .
Wtedy f jest funkcją wewnętrzną, g - zewnętrzną.
Przykład.
Niech
f ( x ) x 1 , g ( x ) x , to
2
4
f : R [1, )
g : [0, ) [0, ) .
Wtedy [1, ) [0, ) i
( g f )( x ) g( f ( x )) g( x 1)
2
4
x 1 dla x R .
2
Analiza Matematyczna 1, Wykład 2
12
13. Slajd 13
Funkcja odwrotnaDla każdej funkcji wzajemnie jednoznacznej f : X Y można
1 1
określić funkcję
f 1 : Y X taką, że
x X , ( f 1 f )( x ) f 1 ( f ( x )) x ,
którą nazywa się funkcją odwrotną.
Własności funkcji odwrotnej:
0
1
2
0
0
3
40
(f ) f
1
1
f ( f ( x )) x id dla x X
1
X
f ( f ( y )) y id dla y Y
1
Y
Wykresy f i f
Funkcja f
1
1
są symetryczne względem prostej y x.
jest odwrotną do f spełnione własności 2 i 3 .
0
Analiza Matematyczna 1, Wykład 2
0
13
14. Slajd 14
Przykładf ( x ) x jest różnowartościowa na [0, ). Funkcja odwrotna f ( x )
1
2
Przykład
f ( x) x
Wtedy f ( x )
1
3
3
x
f : R R .
1 1
x jest funkcją odwrotną funkcji f , bowiem
x R
y R
( y x x y)
3
3
ponieważ
f ( f ( x ))
1
3
1
3
x x i f ( f ( y )) ( y ) ( y ) y
1
3
3
3
3
spełnione są więc własności 2 i 3 .
0
0
Analiza Matematyczna 1, Wykład 2
14
15. Slajd 15
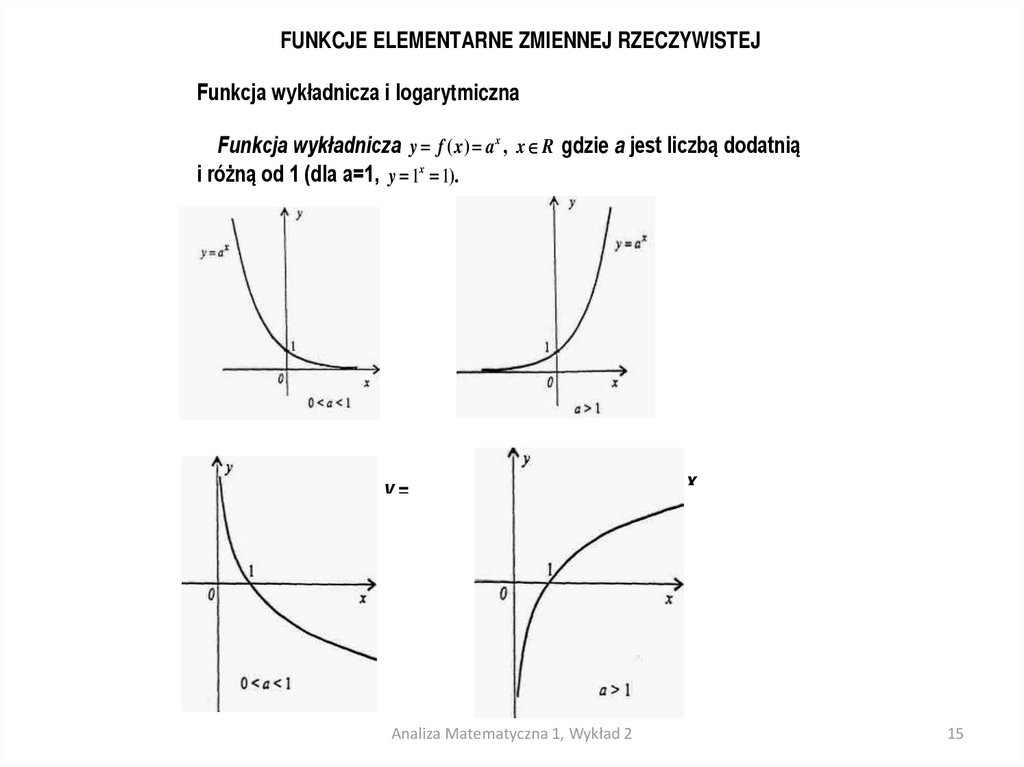
FUNKCJE ELEMENTARNE ZMIENNEJ RZECZYWISTEJFunkcja wykładnicza i logarytmiczna
Funkcja wykładnicza y f ( x) a x , x R gdzie a jest liczbą dodatnią
i różną od 1 (dla a=1, y 1x 1).
y=
y = loga x
Analiza Matematyczna 1, Wykład 2
15
16. Slajd 16
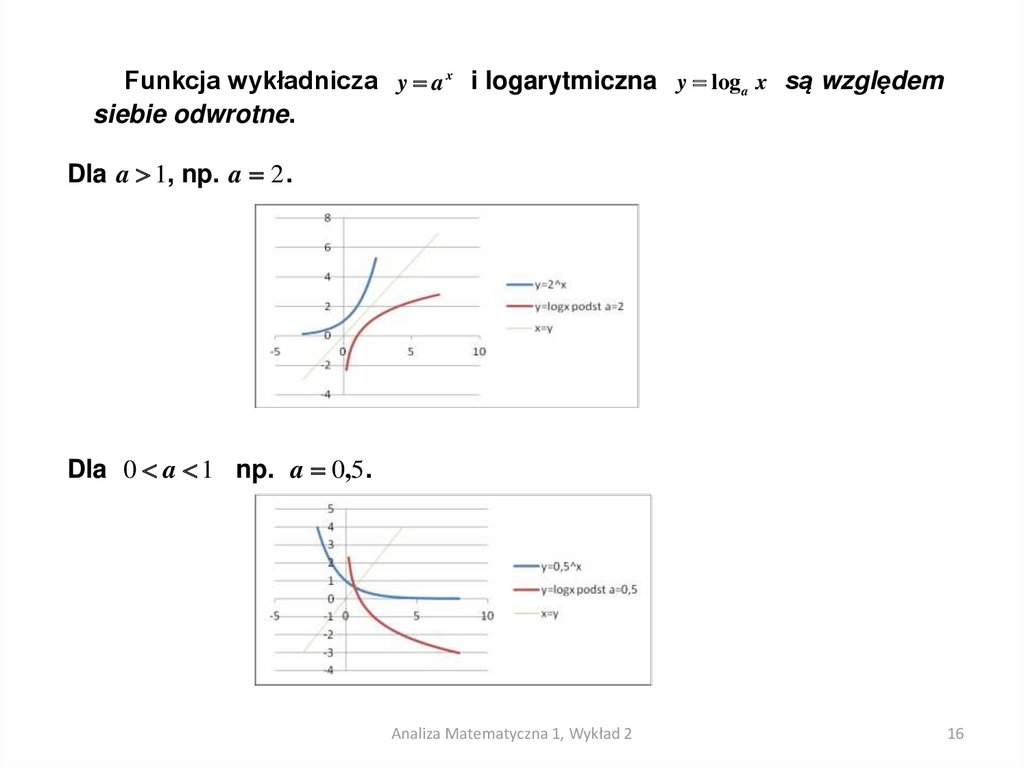
Funkcja wykładnicza y a x i logarytmiczna y log a x są względemsiebie odwrotne.
Dla a 1, np. a 2 .
Dla 0 a 1 np. a 0,5 .
Analiza Matematyczna 1, Wykład 2
16
17. Slajd 17
Reguły potęgowania: ( a 0 i a 1):(a ) a
o
x
1
o
5
k
y
a a
x
x
xy
x
k
o
2
o
6
1
a
3 a
4
a
a a a
a
a
a b (ab) b 0 , x , y R k N
x
x y
y
o
x
o
x
x
x y
y
x
x
Reguły logarytmowania:
1 log xy log x log y
2 log x y log x
x
3 log log x log y
y
log x
4 log x
b 0 i b 1.
log a
o
o
a
a
a
a
a
y
a
a
o
a
o
b
a
b
Złożenie funkcji:
1 log a x x R
o
x
a
o
2 a
loga x
x, x 0, x R
Analiza Matematyczna 1, Wykład 2
17
18. Slajd 18
Wartość bezwzględnaWartość bezwzględna (moduł) liczby rzeczywistej x
Z definicji wynika, że x | x|
x dla x 0
| x|=
-x dla x<0
Dla dowolnych liczb rzeczywistych r, s, zachodzi:
a. | r | | r |
b. | s r | | s | | r |
c. || s | | r || | s r |
d. | s r | jest odległością pomiędzy punktami r oraz s na
prostej rzeczywistej
e. |r s|=|r| | s|
f. | r | 0 r 0
Analiza Matematyczna 1, Wykład 2
18
19. Slajd 19
Funkcje zaokrąglające do liczb całkowitychCzęścią całkowitą liczby rzeczywistej x (podłogą):
x największa liczba całkowita n taka, że n x
x n x n r , 0 r 1,
Powała (sufit) liczby rzeczywistej x:
x =najmniejsza z liczb całkowitych n taka, że x n
1
1
3
3
,
3
3 3 4, 5 5 5
x x x
Analiza Matematyczna 1, Wykład 2
19













 mathematics
mathematics