Sztuczna inteligencja (laboratorium 3)

1.

Sztuczna inteligencja
(laboratorium 3)
Wyższa Szkoła Informatyki i Zarządzania w Rzeszowie
Katedra Sztucznej Inteligencji

2.

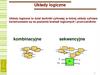
Klasyfikatory 1NN
Klasyfikacja nowego przypadku:
1. poszukujemy punktu w przestrzeni wzorców, który jest
„najbliższy” nowemu przypadkowi
2. przypadek X klasyfikujemy jako należacy do klasy, do
której należy „najbliższy” punkt w przestrzeni wzorców

3.

Klasyfikatory kNN
Klasyfikacja nowego przypadku:
1. poszukujemy k „najbliższych” punktu w przestrzeni
wzorców
2. przypadek X klasyfikujemy jako należący do klasy, która
dominuje w zbiorze k „najbliższych” sąsiadów

4.

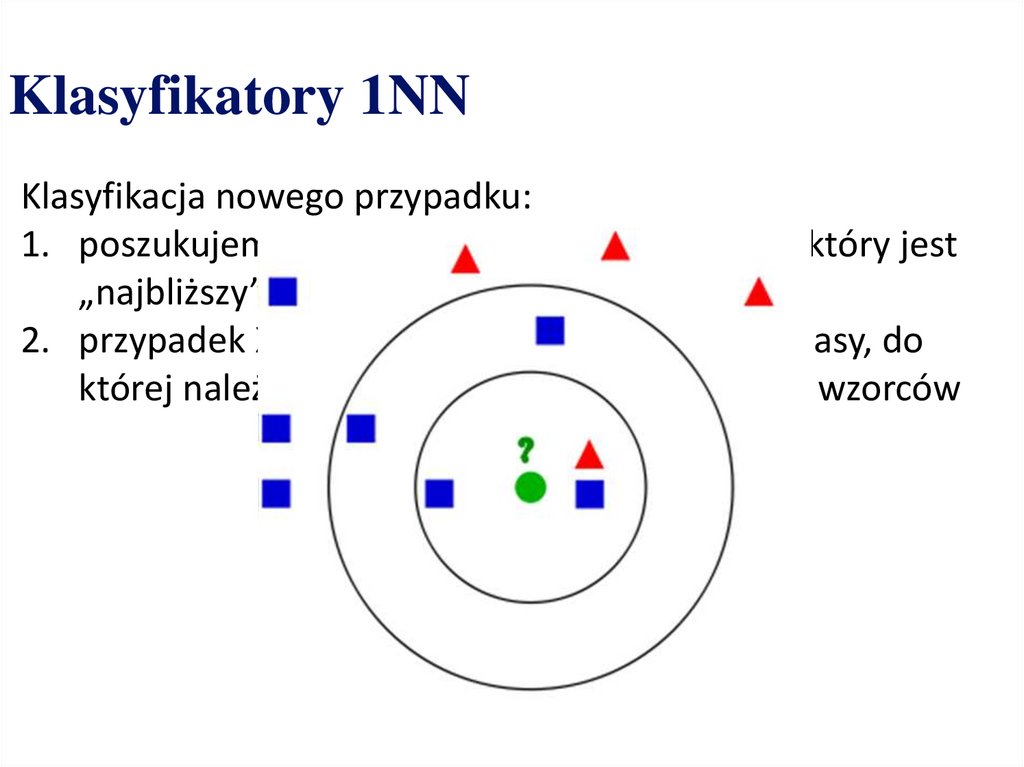
Tablica decyzji
Atrybut_1
Atrybut_2
Atrybut_3 Decyzja
Lp. Symptom_1 Symptom_2 Symptom_3
Diagnoza
1
2
Brak
0
Jest
2
Jest
1 Chory
Jest
1
Brak
0
Brak
0 Chory
3
4
5
Jest
1
Może-jest 1
Jest
1 Chory
Brak
0
Brak
0
Jest
0 Chory
Jest
1
Jest
2
Jest
1 Chory
Brak
0
Brak
0
Jest
1 Zdrowy
Jest
1
Jest
2
Brak
0 Zdrowy
Brak
0
Brak
0
Brak
0 Zdrowy
6
7
8
[W. Traczyk (Red.): Problemy Sztucznej Inteligencji, Wiedza i Życie, Warszawa 1995.]

5.

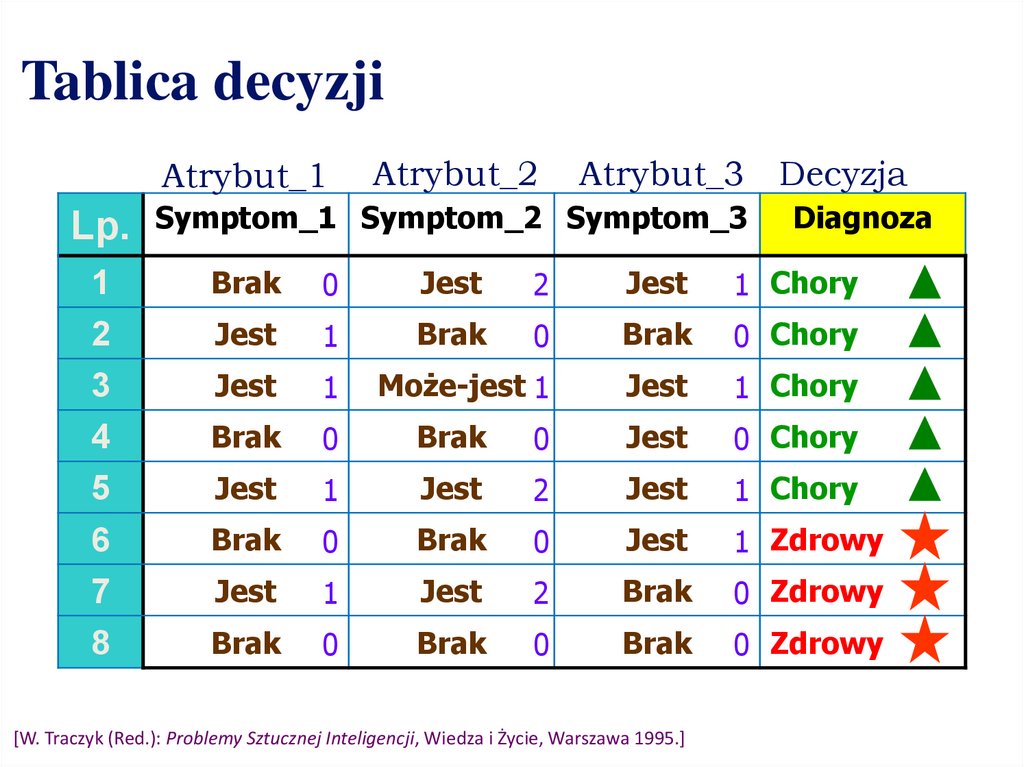
Uczenie metodami opartymi na pomiarze
odległości
Odległość
1. Obliczenie odległości pomiędzy
nieznanym obiektem, a kolejnymi
obiektami w zbiorze uczącym
2. Posortowanie obliczonych dystansów rosnąco
3. Wybranie pewnej liczby k najbliższych obiektów
4. Przeprowadzenie procedury głosowania, jeżeli k jest większe od 1
oraz obiekty należą różnych klas
1
X3
7
6
5
5
3
74
1
3
6 4
1
2
X2
2
1
8
4 6
2 6 8
3 7 7
4 3 4
5 5 1
6 1 5
7 2 2
8 1 3
X1

6.

Funkcje metryk
n
d City Block xi z i
i 1
2
d Euklidesa xi z i
i 1
n
1
2
n
p
d Minkowskiego | xi zi |
i 1
1 dla xi z i
d Symboliczna
i 1 0 dla xi z i
n
n
d Kombinowana (d Euklidesa(N) d Symboliczna (S))
i 1
1
p

7.

3 warunki metryki (odległości)
Przestrzeń metryczna to zbiór Q z określoną na nim funkcją d, która każdym jego dwóm
elementom przypisuje liczbę rzeczywistą dodatnią lub zero, w taki sposób, że dla każdych
X(x1, x2 ... xn), Y(y1, y2 ... yn), Z(z1, z2 ... zn) ze zbioru Q spełnione są następujące warunki:
d ( X ,Y ) 0 X Y
d ( X , Y ) d (Y , X )
d ( X , Z ) d ( X , Y ) d (Y , Z )

8.

Analiza nieznanego obiektu metodą kNN
• należy określić wszystkie odległości pomiędzy klasyfikowanym (nieznanym)
obiektem a wszystkim znanymi obiektami ze zbioru uczącego. Pod pojęciem odległości rozumiemy dystans pomiędzy reprezentującymi obiekty w
przestrzeni n-wielowymiarowej punktami X(x1, x2 ... xn) oraz Z(z1, z2 ... zn).
• uszeregować przypadki ze zbioru uczącego według obliczonej wartości
odległości do nieznanego obiektu, w kolejności od najmniejszej do największej,
• wybrać pewną liczbę k (liczba k jest nieparzystą liczbą całkowitą) obiektów,
znajdujących się najbliżej nieznanego przypadku,
• przypisać nieznanemu obiektowi klasę, która jest najliczniej reprezentowana wśród k najbliższych sąsiadów z zastosowaniem głosowania.

9.

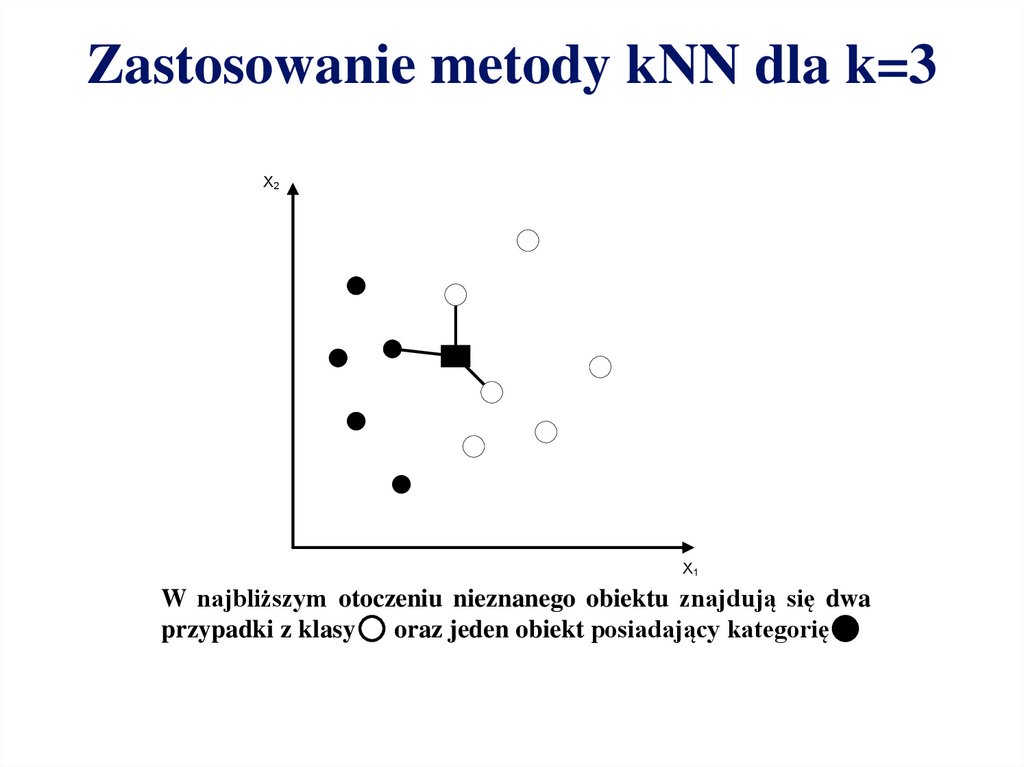
Zastosowanie metody kNN dla k=3
X2
X1
W najbliższym otoczeniu nieznanego obiektu znajdują się dwa
przypadki z klasy
oraz jeden obiekt posiadający kategorię

10.

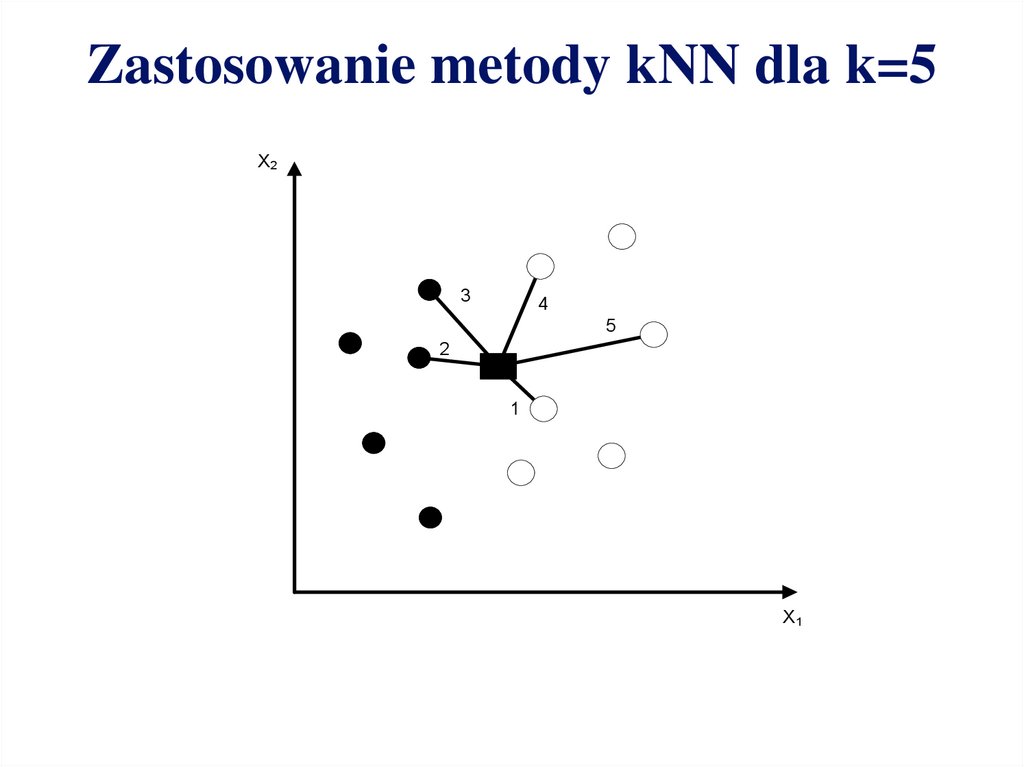
Zastosowanie metody kNN dla k=5
X2
3
4
5
`
2
1
X1

11.

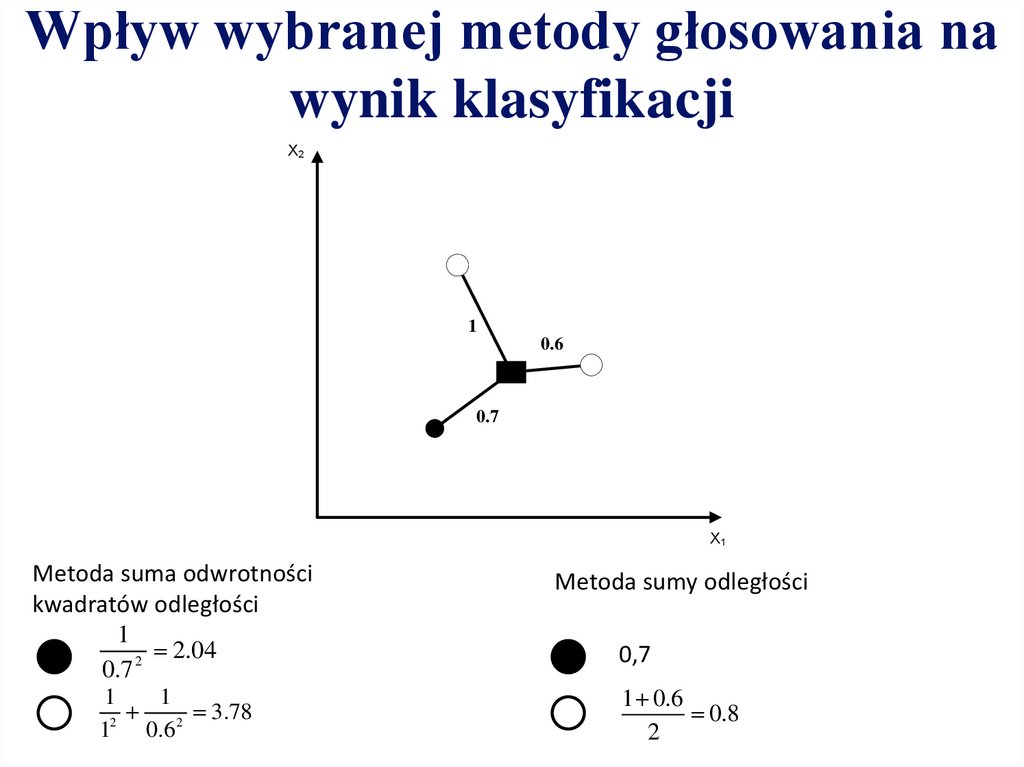
Wpływ wybranej metody głosowania na
wynik klasyfikacji
X2
1
0.6
0.7
X1
Metoda suma odwrotności
kwadratów odległości
1
2.04
0.7 2
1
1
3.78
12 0.6 2
Metoda sumy odległości
0,7
1 0.6
0.8
2

12.

Zadanie praktyczne
Wyznaczyć kategorię dla jednego obiektu nieznanego (za
zbioru testującego) stosując różną liczbę sąsiadów (np. 1,
3, 5), 3 metryki odległości oraz 3 metody głosowania
(normalna, suma odwrotności kwadratów odległości,
sumy odległości)
– Zbiór uczący Bala_L0X.tab
– Zbiór testujący Bala_T0X.tab
X – ostatnia cyfra z numeru indeksu studenta
P_U03
Interpretować uzyskane wyniki eksperymentów w dziedzinie
sztucznej inteligencji wyciągając wnioski badawcze.