Решение задач линейного программирования симплекс-методом. Двойственность ЗЛП

1. Решение задач линейного программирования симплекс-методом. Двойственность ЗЛП.

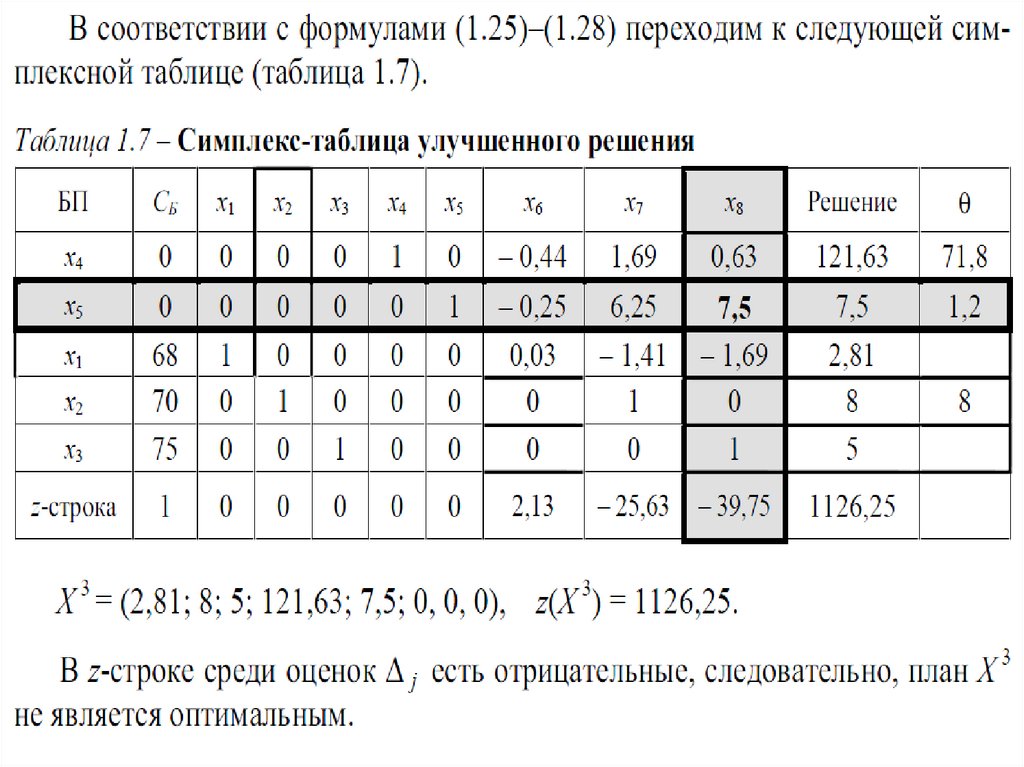
1

2.

1. Основы симплексного метода
2. Пример решения ЗЛП симплексным
методом
3. Основы теории
двойственности ЗЛП
4. Примеры построения
двойственных задач
2

3.

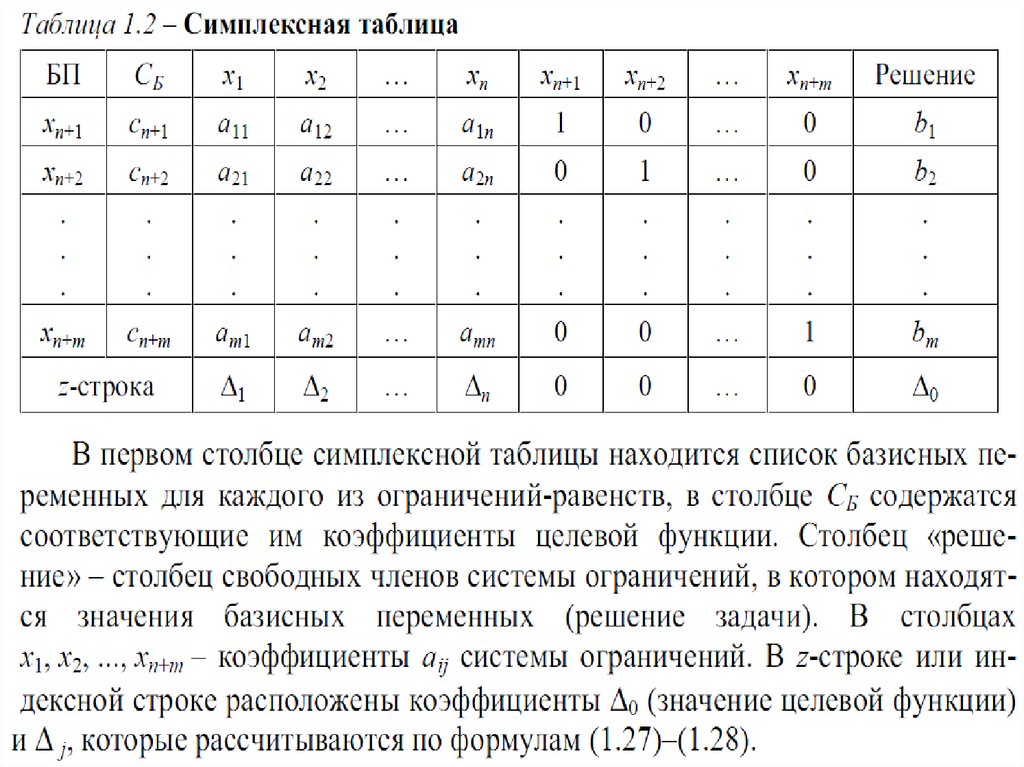
1. Основы симплексного метода
3

4.

4

5.

5

6.

6

7.

7

8.

8

9.

9

10.

10

11.

11

12.

12

13.

13

14.

14

15.

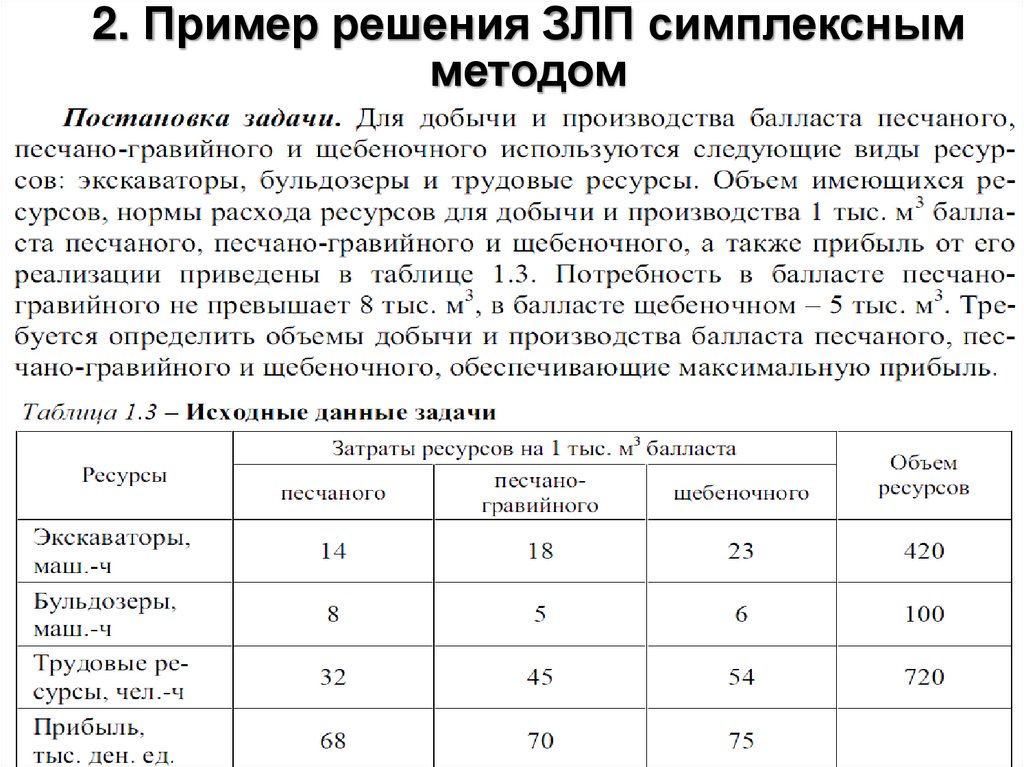
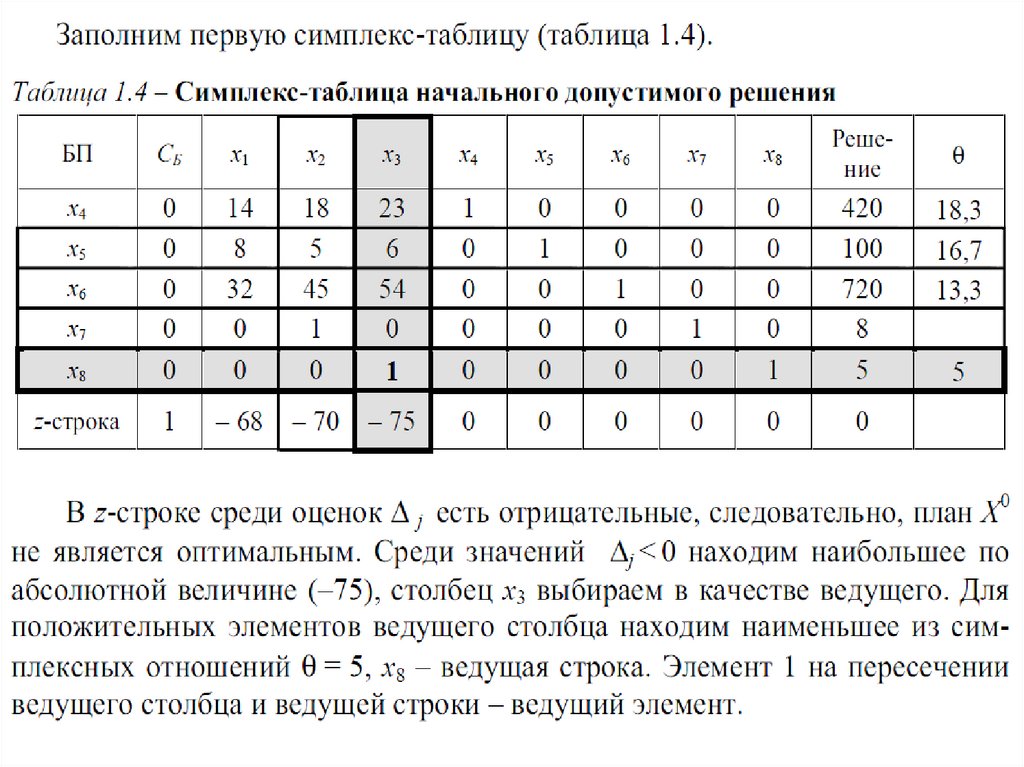
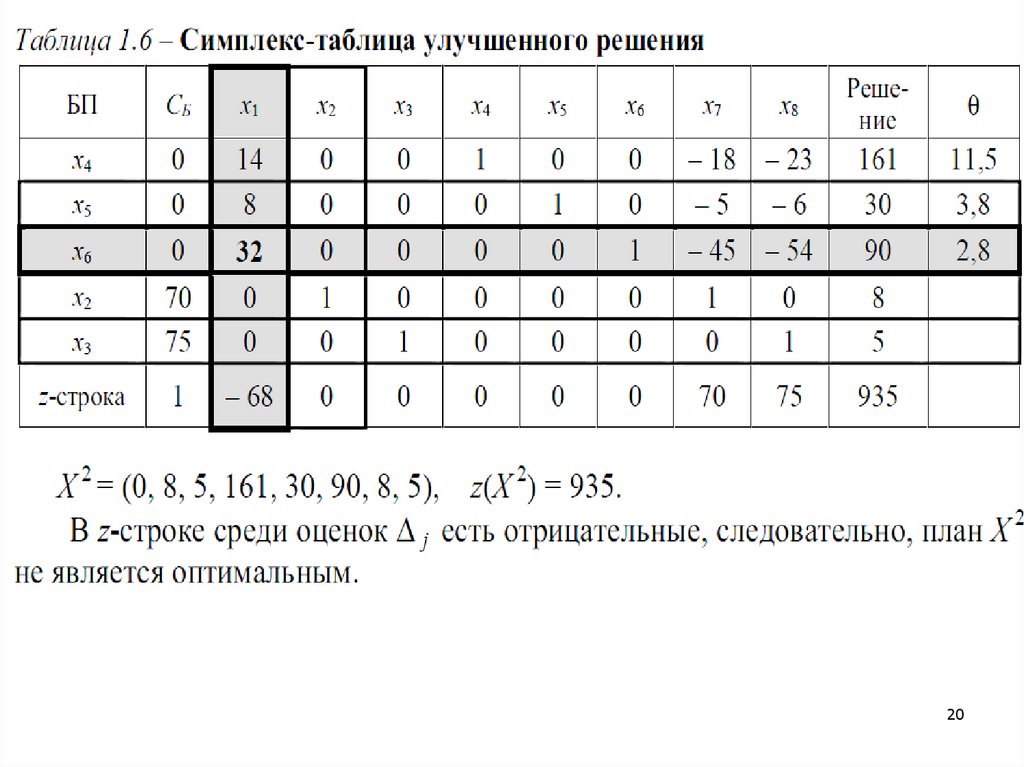
2. Пример решения ЗЛП симплексным
методом
15

16.

16

17.

17

18.

18

19.

19

20.

20

21.

21

22.

22

23.

23

24.

ПРИМЕР РЕШЕНИЯ ЭТОЙ ЖЕ ЗАДАЧИ В
ПАКЕТЕ MATHCAD
24

25.

25

26.

26

27.

3. Основы теории двойственности
ЗЛП
27

28.

МОДЕЛИ ДВОЙСТВЕННЫХ ЗАДАЧ В
ЛИНЕЙНОМ ПРОГРАММИРОВАНИИ
28

29.

29

30.

30

31.

ПРИМЕР
31

32.

32

33.

33

34.

34

35.

ПОЛУЧЕНИЕ РЕШЕНИЯ ДВОЙСТВЕННОЙ
ЗАДАЧИ ПО РЕЗУЛЬТАТАМ РЕШЕНИЯ ПРЯМОЙ
ЗАДАЧИ
Первая теорема двойственности:
Если существует единственное решение
исходной (прямой) задачи, то существует
и единственное решение двойственной
задачи, причем значения целевых функций
на оптимальных решениях совпадают:
max F = min FД.
35

36.

36

37.

При построении двойственной задачи
используются следующие правила:
• каждому ограничению исходной задачи
соответствует переменная двойственной
задачи;
37

38.

• каждой переменной исходной задачи
соответствует ограничение
двойственной, причем коэффициентами
при неизвестных в i-м ограничении
служат коэффициенты при xi в
ограничениях исходной задачи;
38

39.

• коэффициентами при неизвестных в ЦФ
двойственной задачи являются свободные
члены (правые части) в системе
ограничений исходной задачи, а правыми
частями в системе ограничений
двойственной задачи – коэффициенты при
неизвестных в ЦФ исходной, и если
исходная задача формулируется для
нахождения максимума, то двойственная для нахождения минимума (и наоборот).
39

40.

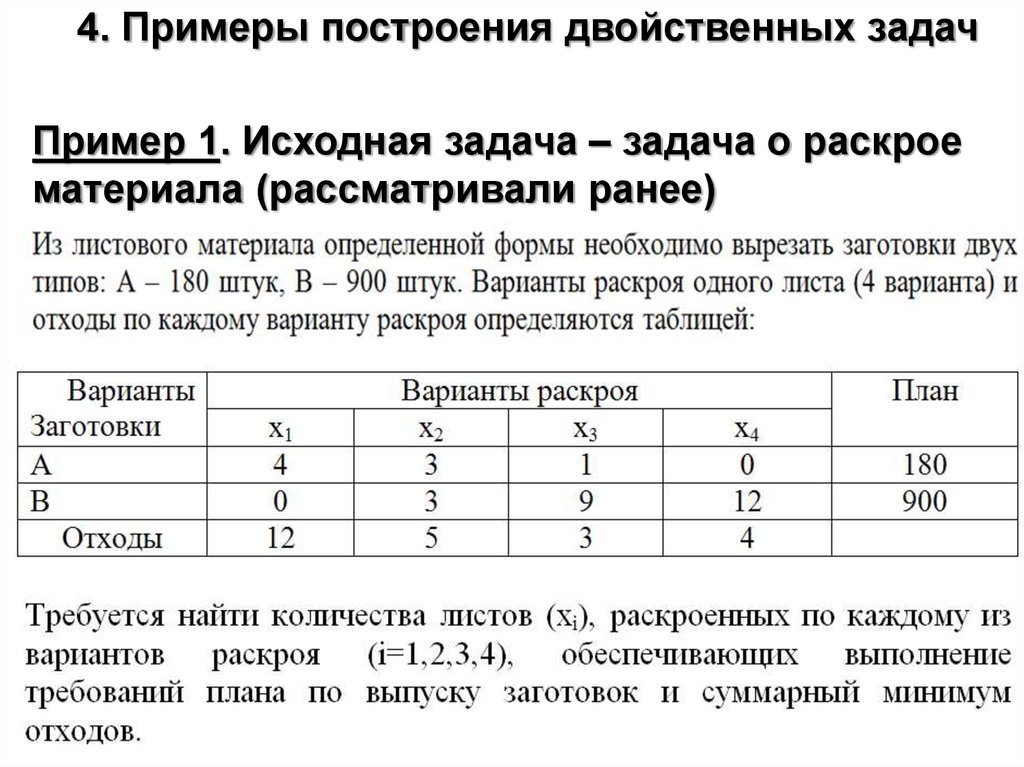
4. Примеры построения двойственных задач
Пример 1. Исходная задача – задача о раскрое
материала (рассматривали ранее)
40

41.

41

42.

42

43.

Кроме того, при использовании
надстройки «Поиск решения» в пакете MS
Excel:
если решить исходную задачу с помощью
этого средства и получить отчет по
устойчивости, то значения в графе
Лагранжа множитель (Теневая цена)
отчета по устойчивости есть оптимальные
значения двойственных переменных:
43

44.

44

45.

Пример 2. Исходная задача – задача о
планировании производства продукции
45

46.

Пример 2. Исходная задача – задача о
планировании производства продукции
46

47.

47

48.

48

49.

Двойственная задача к рассматриваемой
задаче планирования производства продукции:
49

50.

50

51.

Согласно первой теореме двойственности:
51

52.

Для рассматриваемой задачи можно показать,
что имеется следующее следствие первой
теоремы двойственности -
52

53.

(при использовании надстройки «Поиск
решения» в пакете MS Excel).
53

54.

Удобно использовать надстройку
«Поиск решения» в пакете MS Excel:
если решить исходную задачу с помощью
этого средства и получить отчет по
устойчивости, то значения в графе
Теневая цена отчета по устойчивости
есть оптимальные значения
двойственных переменных.
54