Функции нескольких переменных. (Лекция 2)

1. Математика 2 семестр. Лекция № 2.

Функции нескольких
переменных.

2. Понятие о функции нескольких переменных.

Пусть дано некоторое множество D упорядоченных пар чисел (x,y). В
плоскости, отнесенной к прямоугольной декартовой системе координат
OXY, каждой паре чисел (x,y) соответствует точка M(x,y) и наоборот,
каждой точке M(x,y) соответствует пара чисел (x,y). Таким образом,
геометрически множество D представляет собой некоторое множество
точек плоскости OXY.
Определение.
Если в силу некоторого закона каждой паре чисел (x,y) из множества D
ставится в соответствие определенное значение переменной z, то z
называется функцией двух переменных x и y, определенной на множестве
D, и записывается в виде z = f(x,y) или z = f(M).

3. Понятие о функции нескольких переменных.

•Множество D=D(f)
тех точек (x,y) для которых f(x,y)
принимает действительные значения называется областью
определения функции.
•Переменные x и y называются аргументами (независимыми
переменными), а z – зависимой переменной (функцией).
•Множество E=E(f) тех значений z, которые эта переменная
принимает в области определения функции, называется областью
изменения функции, при этом z R
(R - множество
действительных чисел).

4. Пример.

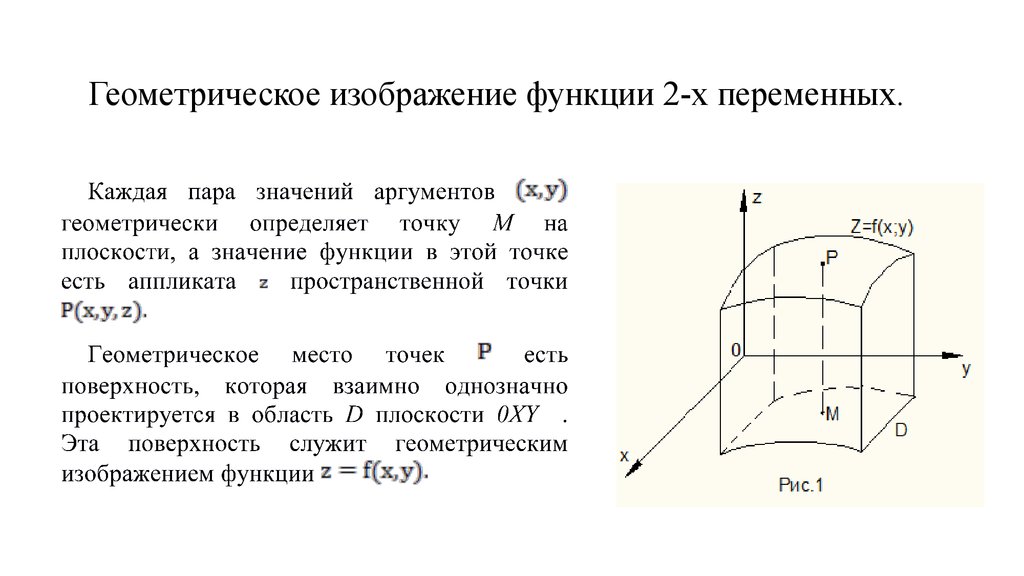
5. Геометрическое изображение функции 2-х переменных.

6.

7. Евклидово n – мерное проcтранство.

8. Понятие функции от любого числа переменных.

9. Пример.

10. Окрестность точки на плоскости.

11. Предел функции нескольких переменных.

12.

13. Непрерывность функции нескольких переменных в точке.

14. Точки и линии разрыва функции.

15.

16. Частные приращения функции.

17. Частные производные первого порядка.

18.

19.

20.

21. Литература.

• Боронина Е.Б. Математический анализ [Электронный ресурс]:
учебное пособие/ Боронина Е.Б.— Электрон. Текстовые данные.
— Саратов: Научная книга, 2012.— 159 c.— Режим доступа:
http://www. iprbooksho p.ru/6298. — ЭБС «IPRbooks»
• Письменный, Д. Т. Конспект лекций по высшей математике.
Полный курс [Текст] : [учебное пособие] / Д. Т. Письменный. - 9-е
изд. - Москва : Айрис-пресс, 2010. - 603 с. : ил., табл. - (Высшее
образование). - ISBN 978-5-8112-4073-9
• Шипачев, В. С. Курс высшей математики [Текст] : учебник для
вузов / В. С. Шипачев ; под ред. А. Н. Тихонова ; - 4-е изд., испр. Москва : Оникс, 2009. - 600 с. : ил. - ISBN 978-5-488-02067-2