Similar presentations:
Вычисление натурального логарифма. Лекция 4
1.
Вычисление натурального логарифмаНачнем с известного представления рядом Тейлора функции натурального
логарифма в окрестности 1.
n
x 2 x3 x 4
n 1 x
Ln(1 x) x
... ( 1)
... ,
2
3
4
n
1 x 1
Недостатки этого представления: 1) диапазон чисел узкий; 2) для
значений х, близких по модулю к 1, сходимость ряда становиться
медленной.
Получим другое представление для натурального логарифма.
x2
x3
xn
Ln(1 x) x
...
...
2
3
n
Найдем разность этих представлений
1 x
x3
x5
Ln
2( x
...)
1 x
3
5
Обозначим
1 x
z
1 x
, откуда
x=(1-z) / (1+z) .
2.
В результате получим1 z 1 1 z 3 1 1 z 5
ln z 2
,
1 z 3 1 z 5 1 z
при 0 z
Диапазон чисел расширили.
Пусть х – положительное число, логарифм которого надо вычислить.
Представим его в виде произведения х=2m * q, где 0.5 ≤ q < 1, и далее
обозначим 1 q где 0 1 1 / 2 1
1 1/ 2 3
1 q
Теперь логарифм числа х можно представить в виде
3
2 n 1
Rn
ln x ln 2 q m ln 2 ln q m ln 2 2
3
2n 1
m
Остаточный член, по определению, имеет вид (заменa знаменателей во всех
слагаемых на 2n+1)
2 n 1
2 n 3
2n 1
Rn 2
... 2
1 2 4 ...
2n 1
2n 1 2n 3
3.
В правой части неравенства, в круглых скобках - бесконечнаягеометрическая прогрессия, со знаменателем меньшем 1. Сумма такой
прогрессии легко находится, и равна
1
1 2
Получаем неравенство для остаточного члена
2 2 n 1
Rn
1 2 2n 1
1
Если учесть, что 0
3
тогда можно записать
2
9
1 2 4
9 2 n 1
Следовательно получаем неравенство:
0 Rn
4 2n 1
Или более грубо:
1
1
0 Rn
4 2n 1 3
2 n 1
4.
Сам вычислительный процесс можно организовать следующим образом.Обозначим
Uk
2 k 1
2k 1
тогда можно получить
, k 1, 2, ...
Ln( x) mLn(2) 2(U 1 U 2 ... U n ) Rn
Считая, что Ln(2) = 0.69314708 вычисление логарифма любого
положительного числа не представляет труда.
Окончание процесса суммирования производим тогда, когда U n 4 R
где R остаточная погрешность.
В самом деле, в этом случае имеем
9 2 2 n 1 1
Rn
Un R
4
2n 1 4
5.
Вычисление значений тригонометрических функцийФункция SIN(x)
Используя формулы приведения, значение аргумента х можно привести к
интервалу
0 x
2
Для значений аргумента
.
0 x
4
x 2 n 1
n
Sin ( x) 1
2n 1 !
n 0
Для значений аргумента
4
можно получить
x
(1)
2
z 2n
Sin ( x) Cos( z ) ( 1)
( 2 n) !
n 0
n
z
2
x, 0 z
4
(2)
6.
Сумму ряда удобно вычислять путемSin( x) U 1 U 2 U 3 ... U n Rn
где слагаемые U k можно последовательно находить по рекуррентным
формулам
U1 x
x2
U k 1
Uk
2k (2k 1)
, (k 1, 2, ..., n 1)
Ряд (1) знакочередующийся, с монотонно убывающими по модулю
членами. Тогда остаточный член можно записать
x 2 n 1
Rn
U n 1
(2n 1) !
sign ( Rn ) sign (U n 1 )
Поэтому процесс суммирования можно прекратить, как только
обнаружится, что | U | ,
заданная остаточная
R
n
R
погрешность.
7.
Вычисление значений тригонометрических функцийФункция COS(x)
x 2n
cos( x) 1
2n !
n 0
Сумму ряда удобно вычислять путем
n
cos x v1 v2 ... v n Rn
где слагаемые vn
формулам
можно последовательно находить по рекуррентным
x2
v1 1, vk 1
vk
2k 1 2k
k 1, 2, ..., n 1
Ряд знакочередующийся, с монотонно убывающими по модулю членами.
Тогда остаточный член можно записать
x 2n
Rn
vn 1 ,
2n !
sgn Rn sgn vn 1
Поэтому процесс суммирования можно прекратить, как только
обнаружится, что | vn | R , R заданная остаточная
погрешность.
8. Итеративные методы вычисления значений функций
Задана функцияy f (x )
функции в точке
надо вычислить значение
x ,то есть
y f ( ).
Запишем функцию в неявном виде F ( x, y ) 0.
Предположим, что F x, y - непрерывна и имеет непрерывную
частную производную Fy x, y .
Тогда
F ( , y ) 0
9. Итеративные методы вычисления значений функций
F x, y 0По теореме Лагранжа о непрерывных функциях:
F x, y0 F x, y F x, y 0 0 y0 y Fy x, y
где
Тогда
y
промежуточное значение между
F x, y0
y y
Полагая
0
y y0
y0
и y.
Fy x, y
, получим:
y1 y0
F x, y0
Fy x, y 0
Повторяя этот алгоритм, получим итеративный процесс:
yn 1 yn
F x, yn
Fy x, y n
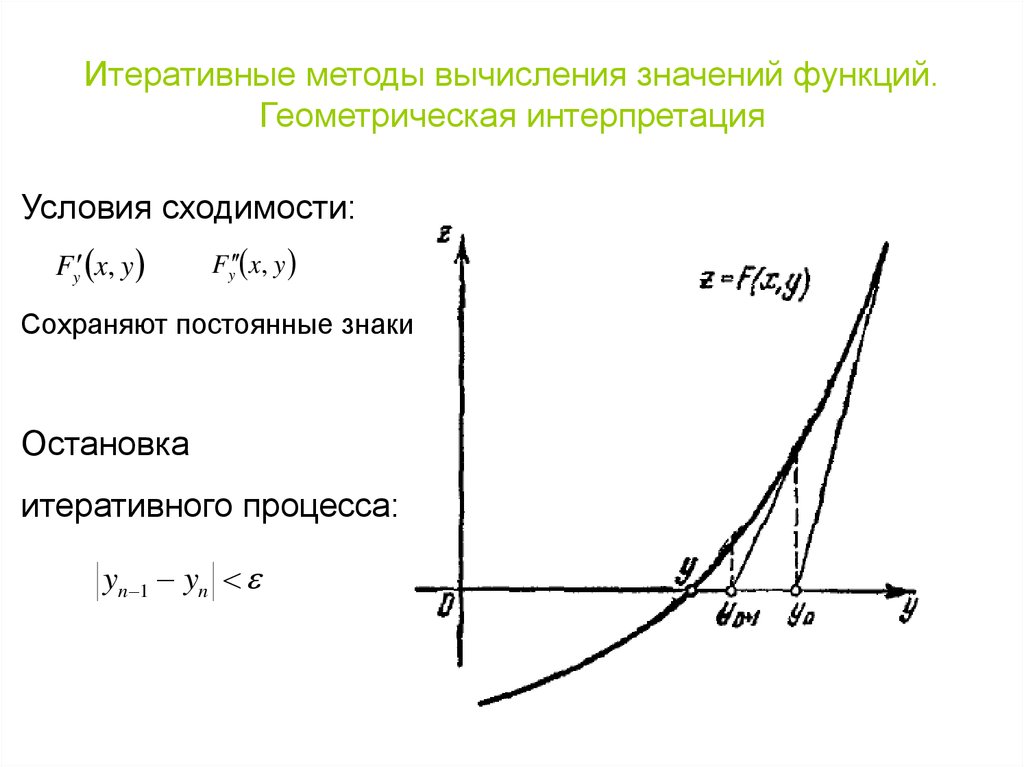
10. Итеративные методы вычисления значений функций. Геометрическая интерпретация
Условия сходимости:Fy x, y
Fy x, y
Сохраняют постоянные знаки
Остановка
итеративного процесса:
yn 1 yn









 mathematics
mathematics








