Similar presentations:
Информатика в задачах теплоэнергетики
1. Информатика в задачах теплоэнергетики Лекция №2
2. Решение задач интерполяции в теплоэнергетике
В результате эксперимента по определениюхолостого
хода
определена
зависимость
потребляемой из сети мощности (Po, Вт) от входного
напряжения (U, В) для электрического асинхронного
двигателя вращающего центробежный насос.
U,
В
132
140
150
162
170
180
190
200
211
220
232 240
251
U,
Вт 330
350
385
425
450
485
540
600
660
730
920 1020
1350
Построить
график
зависимости P(U).
интерполяционной
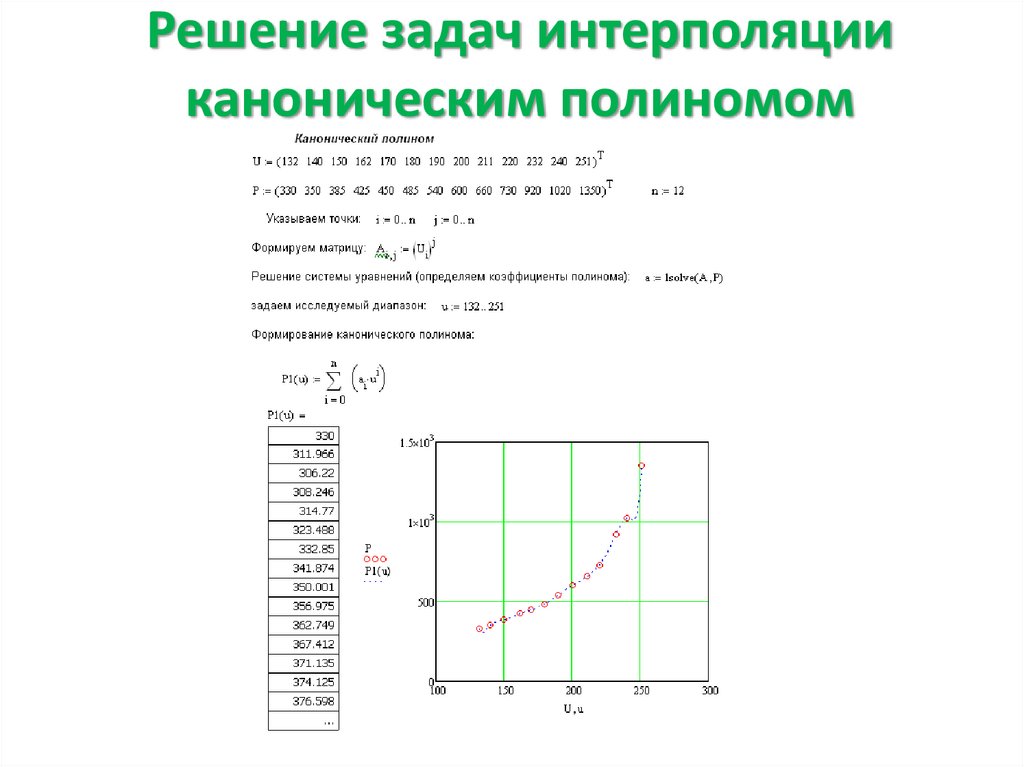
3. Решение задач интерполяции каноническим полиномом
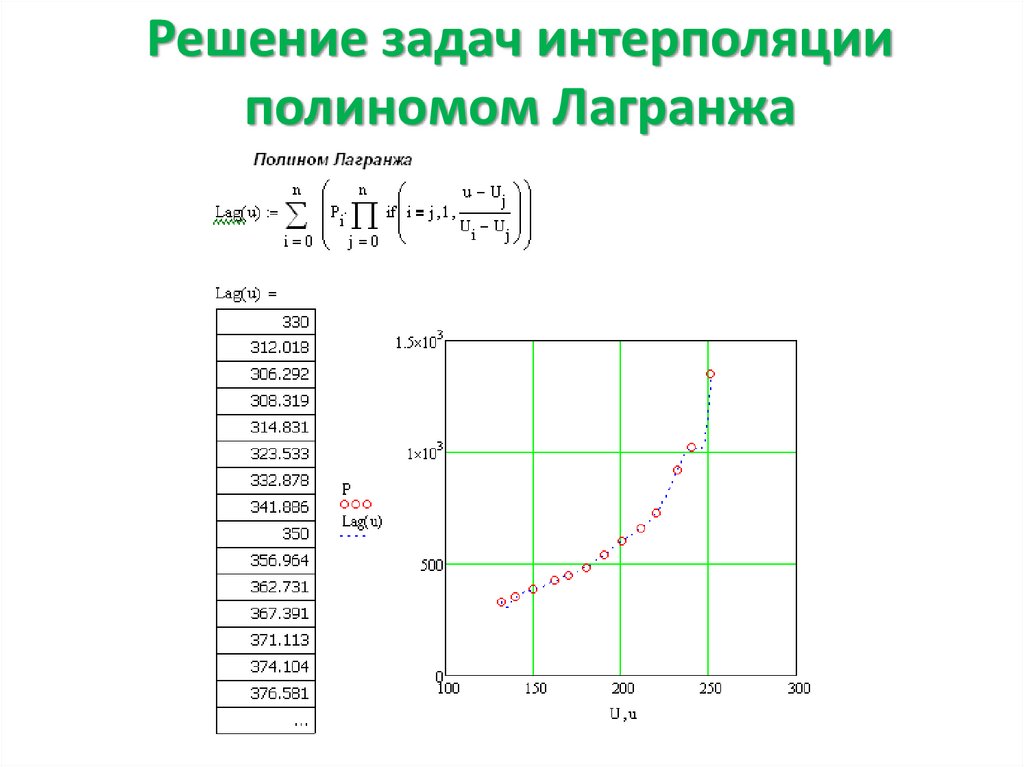
4. Решение задач интерполяции полиномом Лагранжа
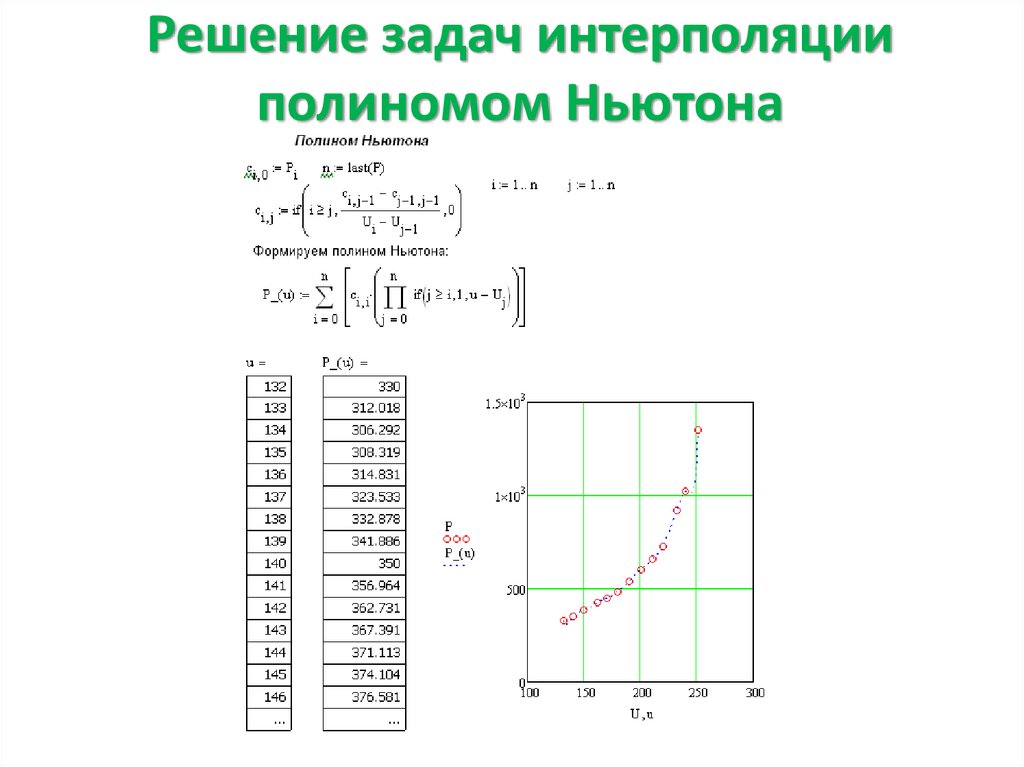
5. Решение задач интерполяции полиномом Ньютона
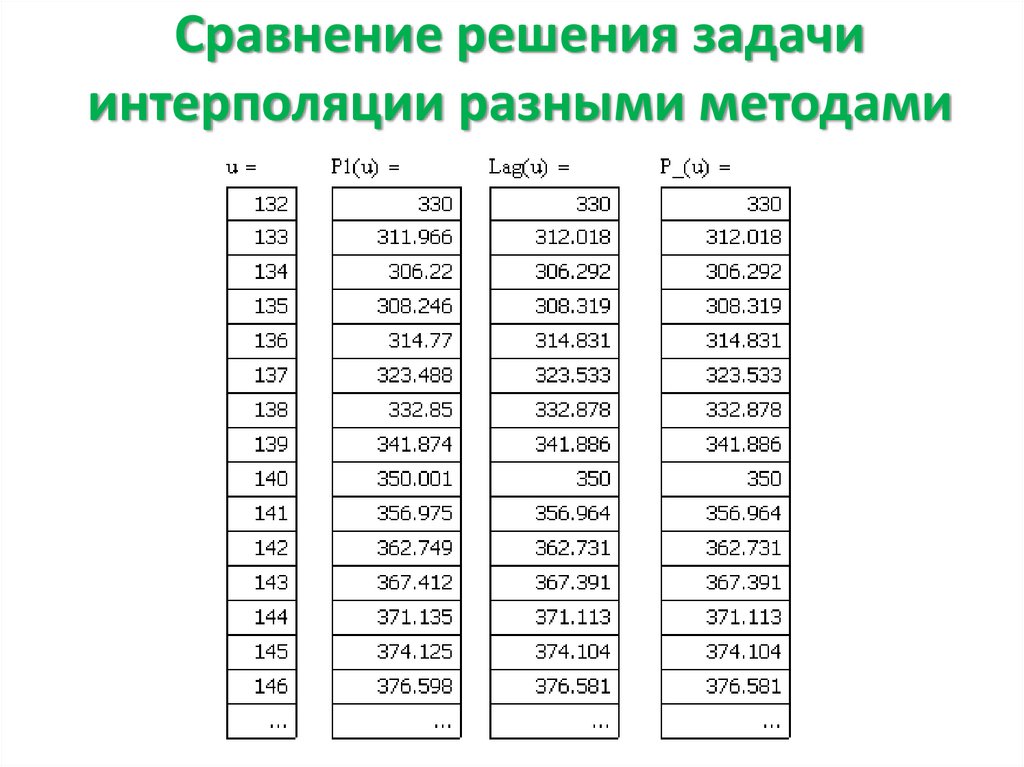
6. Сравнение решения задачи интерполяции разными методами
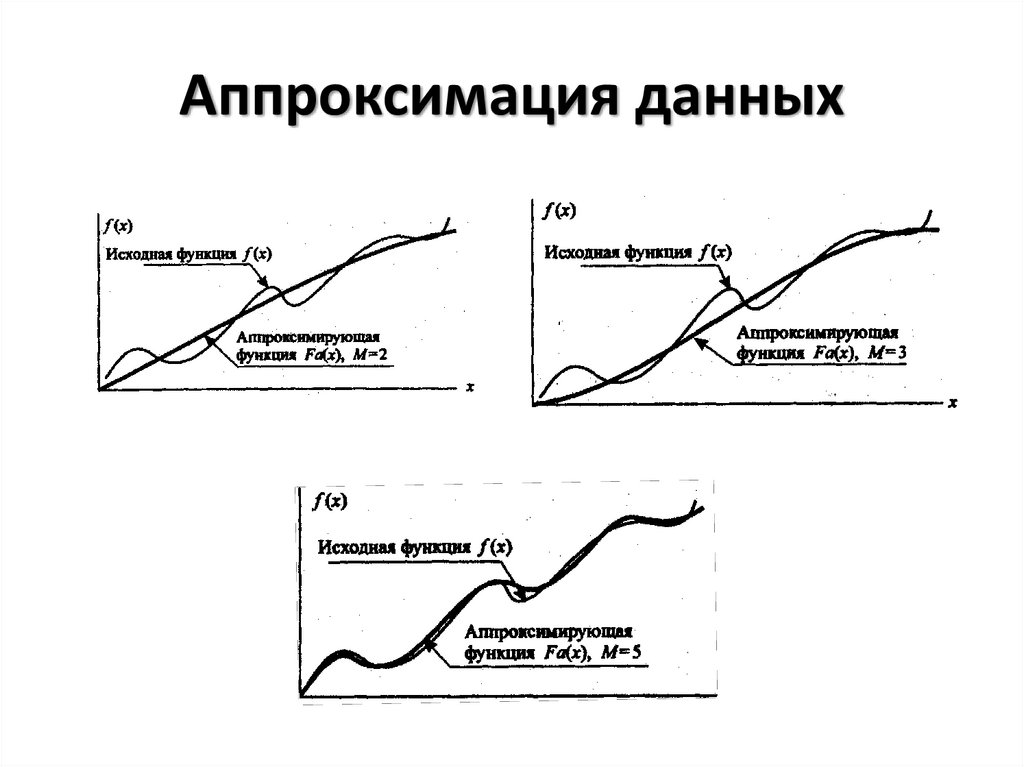
7. Аппроксимация данных
Основнаязадача
аппроксимации
–
построение
приближенной
(аппроксимирующей)
функции,
в
целом
наиболее близко проходящей около данных
точек или около данной непрерывной функции.
Такая
задача
возникает
при
наличии
погрешности в исходных данных (в этом случае
нецелесообразно проводить функцию точно
через все точки, как в интерполяции) или при
желании получить упрощенное математическое
описание
сложной
или
неизвестной
зависимости.
8. Аппроксимация данных
Близость исходной и аппроксимирующей функцийопределяется числовой мерой – критерием
аппроксимации
(близости).
Наибольшее
распространение получил квадратичный критерий,
равный сумме квадратов отклонений расчетных
значений от "экспериментальных" (т.е. заданных), –
критерий близости в заданных точках:
n
R
расчет. 2
(y i y i
) .
i 1
Квадратичный
критерий
обладает
рядом
"хороших"
свойств,
таких,
как
дифференцируемость, обеспечение единственного решения задачи аппроксимации при
полиномиальных аппроксимирующих функциях.
9. Аппроксимация данных
R max y i y iрасчет. .i
Этот критерий менее распространен в связи с аналитическими
и вычислительными трудностями, связанными с отсутствием
гладкости функции и ее дифференцируемости.
В обоих рассмотренных случаях в качестве значения функции у
можно брать не только абсолютные, но и относительные
значения, например: уi /уn и другие.
Выделяют две основные задачи аппроксимации:
1) получение аппроксимирующей функции, описывающей
имеющиеся данные, с погрешностью не хуже заданной;
2) получение аппроксимирующей функции заданной структуры с
наилучшей возможной погрешностью.
Чаще всего первая задача сводится ко второй путем перебора
различных аппроксимирующих функций с последующим выбором
наилучшей.
10. Аппроксимация данных
11. Метод наименьших квадратов
Метод базируется на применении в качестве критерияблизости суммы квадратов отклонений заданных и
расчетных
значений.
При
заданной
структуре
аппроксимирующей функции уiрасчет.(х) необходимо
подобрать параметры этой функции таким образом, чтобы
получить наименьшее значение критерия близости, т.е.
наилучшую аппроксимацию.
y iрасчет.(x) ak x k
ak 1 x
n
k
i 1
j 0
k 1
k
... a0 a j x j ;
R (y i a j x ij )2 .
j 0
12. Метод наименьших квадратов
Искомые переменные aj можно найти изнеобходимого условия минимума R по этим
переменным, т.е. dR/dap =0 (для р = 0,1,2,...,К).
Продифференцируем по ap (р – текущий
индекс):
dR/dap 2 (y
p
a j xi )( xi )
j
где р=0,1,2,…,к, i=1,2,…,n.
0,
13. Метод наименьших квадратов
После очевидных преобразований (сокращение надва, раскрытие скобок, изменение порядка
суммирования) получим:
dR/dap y i (-x ip ) a j x ij x ip y j ( x ip ) a j x ij x ip 0,
j
i
j
i
j
где р=0,1,2,…,к.
Перепишем последние равенства:
j p
p
a
x
x
y
x
j i i i i ,
j
i
i
i
14. Метод наименьших квадратов
Получилась система n+1 уравнений с таким же количествомнеизвестных aj, причем линейная относительно этих переменных. Эта
система называется системой нормальных уравнений. Из ее решения
находятся параметры aj аппроксимирующей функции, обеспечивающие
min R, т.е. наилучшее возможное квадратичное приближение. Зная
коэффициенты, можно (если нужно) вычислить и величину R (например,
для сравнения различных аппроксимирующих функций). Следует
помнить, что, при изменении даже одного значения исходных данных
(или пары значений хi, уi, или одного из них), все коэффициенты изменят
в общем случае свои значения, так как они полностью определяются
исходными данными. Поэтому при повторении аппроксимации с
несколько
изменившимися
данными
(например,
вследствие
погрешностей измерения, помех, влияния неучтенных факторов и т.п.)
получится другая аппроксимирующая функция, отличающаяся
коэффициентами.
15. Метод наименьших квадратов
nn
a0 n a1 xi yi
i 1
i 1
полином
1
порядка
n
n
n
2
a
0 xi a1 xi xi yi
i 1
i 1
i 1
- полином
n-го порядка
m
m
m
m
2
n
ma0 xi a1 xi a 2 xi a n yi
i 0
i 0
i 0
i 0
m
m
m
m
2
n 1
xi a0 xi a1 xi a n xi yi
i 0
i 0
i 0
i 0
m
m
m
m n
n 1
2n
n
x
a
x
a
x
a
x
i n i yi
i 0 i 1
i 0
i 0
i 0
i 0
16. Метод наименьших квадратов
Дана таблично заданная функция (табл. 1.1.).Требуется найти аппроксимирующую функцию в виде
линейного полинома у=а0+а1х по имеющимся
экспериментальным данным.
Таблица 1.1.
Данные для аппроксимации по МНК
n
(кол-во точек)
оС
t,
h, кДж/кг
h
расчет
0
1
2
3
10
42,04
20
125,70
30
209,30
40
355,00
a 0 a1ti
n
R (hi a0 a1ti ) 2
Найдем производные по а0 и а1:
i 1
dR
da 0
0
dR 0
da1
17. Метод наименьших квадратов
n2 (hi a0 a1ti )( 1) 0
i 1
n
2 (h a a t )( t ) 0
i
0
1 i
i
i 1
Проведя преобразования, получим:
n
(a0 a1ti hi ) 0
i 1
n
(a t a t 2 h t ) 0
0 i
1 i
i i
i 1
18. Метод наименьших квадратов
Система нормальных уравнений для полинома 1 степени будет выглядеть следующим образом:n
n
a0 n a1 ti hi
i 1
i 1
n
n
n
2
a
t
a
t
0 i
1 i ti hi
i 1
i 1
i 1
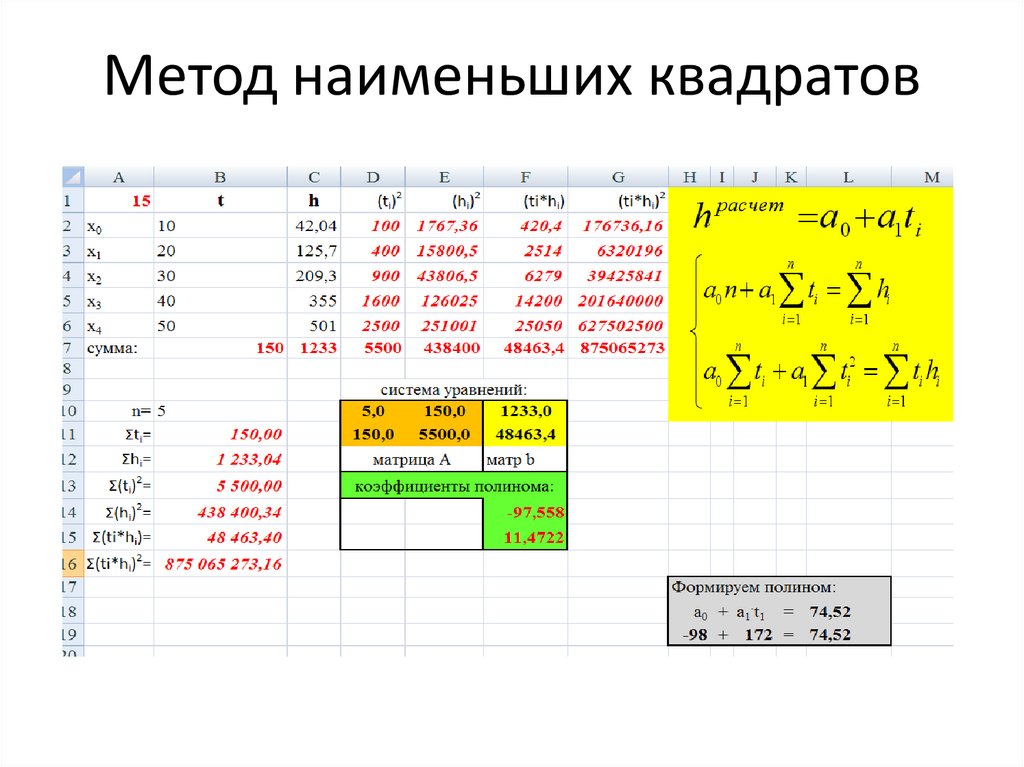
Используя имеющиеся данные, получим:
n=5, ti=150, ti2=5500, hi=1233, hiti=48463;
a0 5 a1150 1233
a0150 a1 5500 48463
Решив полученную систему линейных уравнений относительно
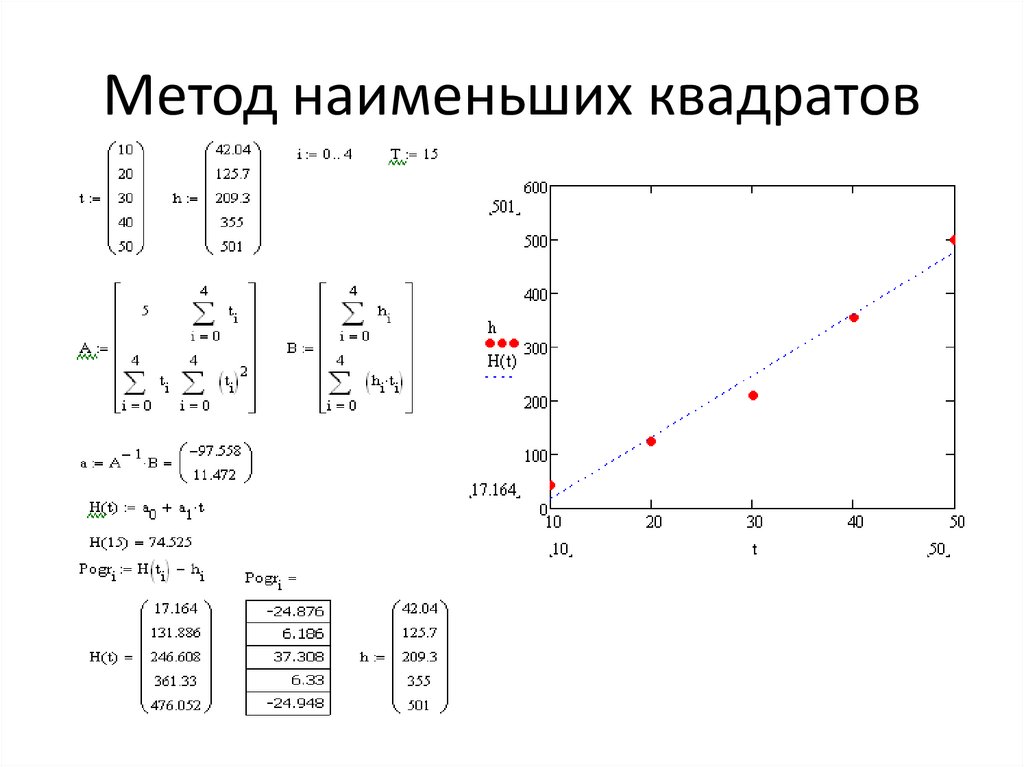
а0 и a1, получим а0=-97,6; a1 =11,47.
Аппроксимирующая функция имеет вид: h(t)= -97,6 + 11,47ti
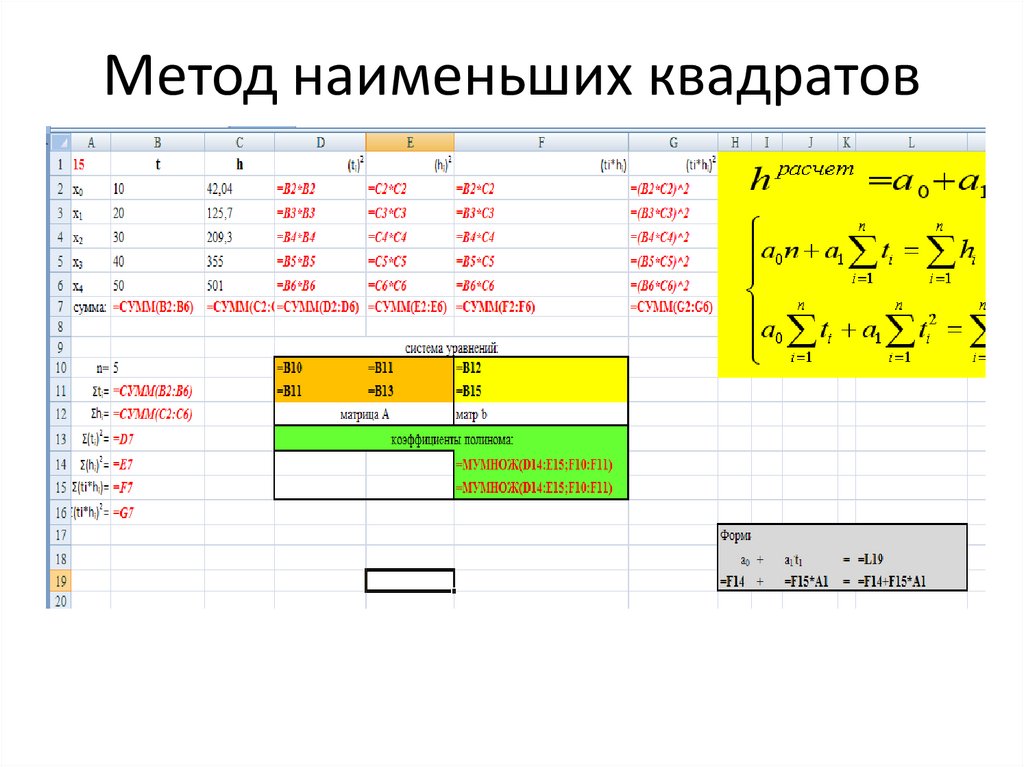
19. Метод наименьших квадратов
20. Метод наименьших квадратов
21. Метод наименьших квадратов
22. Метод неопределенных коэффициентов
Метод базируется на составлении и решениисистемы линейных уравнений. При заданной
системе уравнений необходимо подобрать
параметры этой функции таким образом, чтобы
получить наименьшее значение критерия
близости, т.е. наилучшую аппроксимацию. При
этом составляется система уравнений исходя из
заданных начальных значений.
23. Метод неопределенных коэффициентов
y P( x) a0 a1 x a2 x a3 x ... an x2
3
n
Затем строим матрицу:
a0 a1 x a2 x a3 x a x x
a a x a x a x a x
2
3
x
0 1
a0 a1 x a2 x a3 x a x x
a a x a x a x a x
2
3
x
0 1
a0 a1 x a2 x a3 x a x x
y
y
y
y
y
Решаем систему (находим коэффициенты полинома)
и формируем полином n-ой степени.

















 mathematics
mathematics








