Функция. Способы задания функций

1. Отчет по практической работе №1 По дисциплине: «Информатика»

Отчет по практической работе №1
По дисциплине: «Информатика»
ВЫПОЛНИЛА: ГОЛУБЕВА ЕЛЕНА

2. Функция

Числовой функцией называется соответствие (зависимость), при
котором каждому значению одной переменной сопоставляется
по некоторому правилу единственное значение другой
переменной
Если установить соответствия, то — это называется функция,
где x - область определения, y - область значения,
а f – соответствие
y f (x)
— явно заданная функция
f ( x, y ) 0
— не явно заданная функция

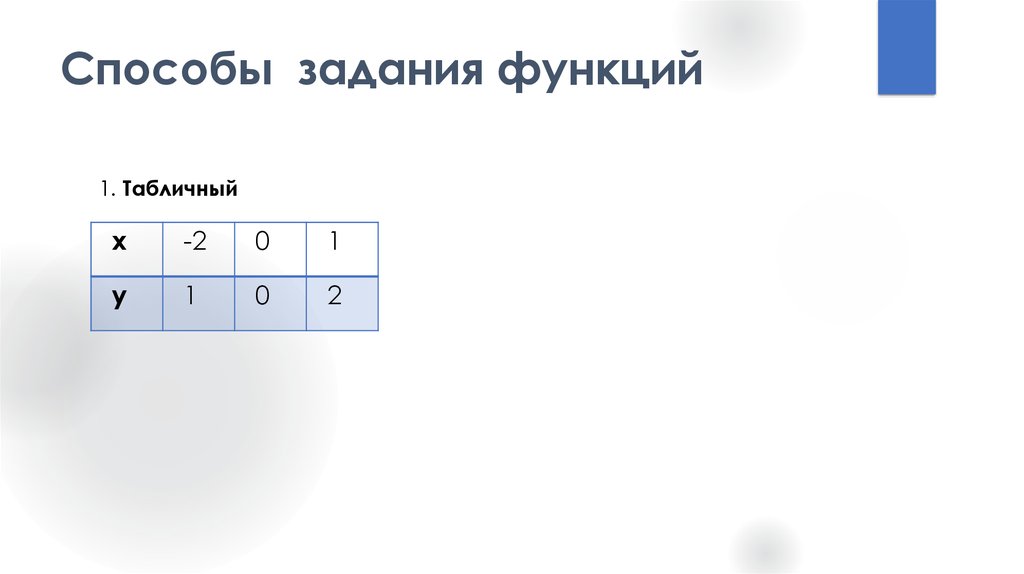
3. Способы задания функций

1. Табличный
x
-2
0
1
y
1
0
2

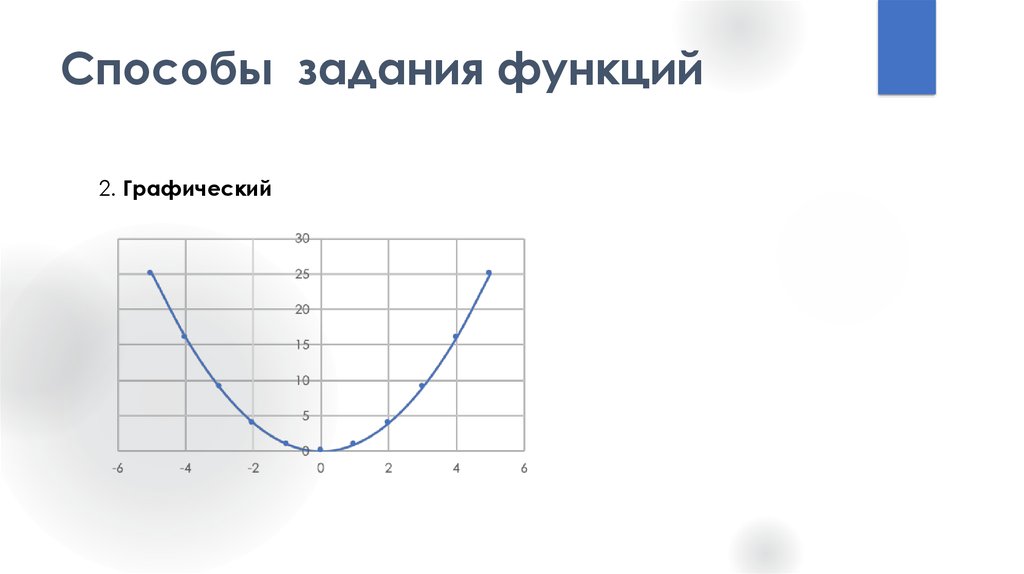
4. Способы задания функций

2. Графический

5. Способы задания функций

3. Аналитический — это когда функция задается через формулу
y cos x
4. Словесный
Пример: Сила равна скорости изменения импульса

6. Виды функций

1.
Элементарная — это линейная, степенная, квадратичная,
показательная, тригонометрическая и т. д
2.
Иррациональная функция
3.
Трансцендентная функция
4.
Гиперболические — разновидность тригонометрических
e x e x
sin x
2
sec x
e x e x
cos x
2
cos ecx
sin x
tan x
cos x
sin 2 x cos 2 x 1
1
cos 2
1
sin 2

7. Свойства функций

1. Область определения
D(x) y Sinx
D(x)=R – все действительные числа y
2. Область значения E(y)
1
,x≠1
x 1

8. Свойства функций

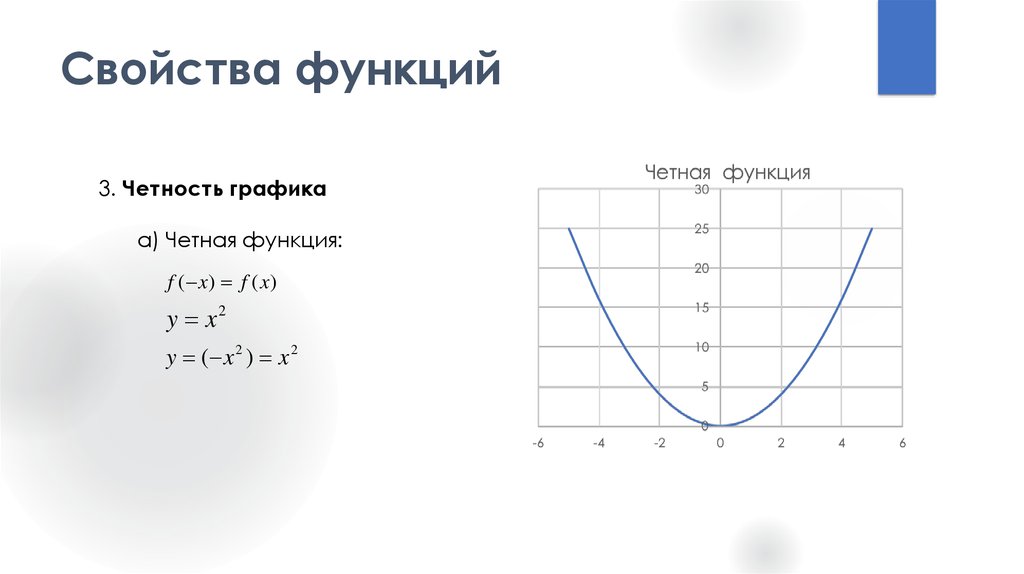
3. Четность графика
а) Четная функция:
f ( x) f ( x)
y x2
y ( x 2 ) x 2

9. Свойства функций

Нечетная функция
150
100
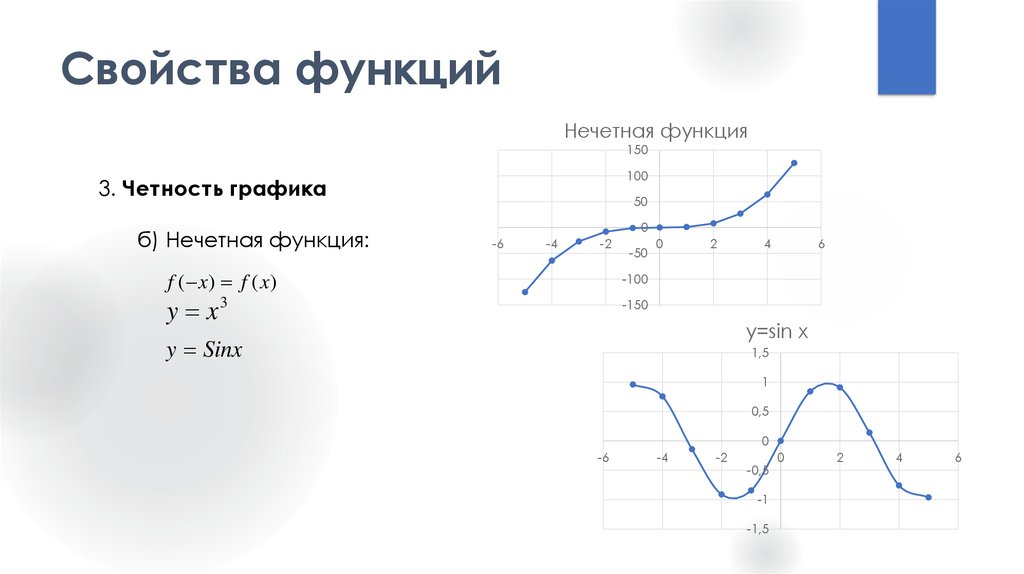
3. Четность графика
б) Нечетная функция:
50
0
-6
-4
-2
f ( x) f ( x)
-50
0
2
4
6
-100
y x3
-150
y=sin x
y Sinx
1,5
1
0,5
0
-6
-4
-2
-0,5
-1
-1,5
0
2
4
6

10. Свойства функций

4. Периодичность функции
y f (x)
называется периодической, если существует такое
положительное число J>0,что для всех x из области определения числа
выполняется равенство f ( x J) = f(x)
Примером является любая тригонометрическая функция
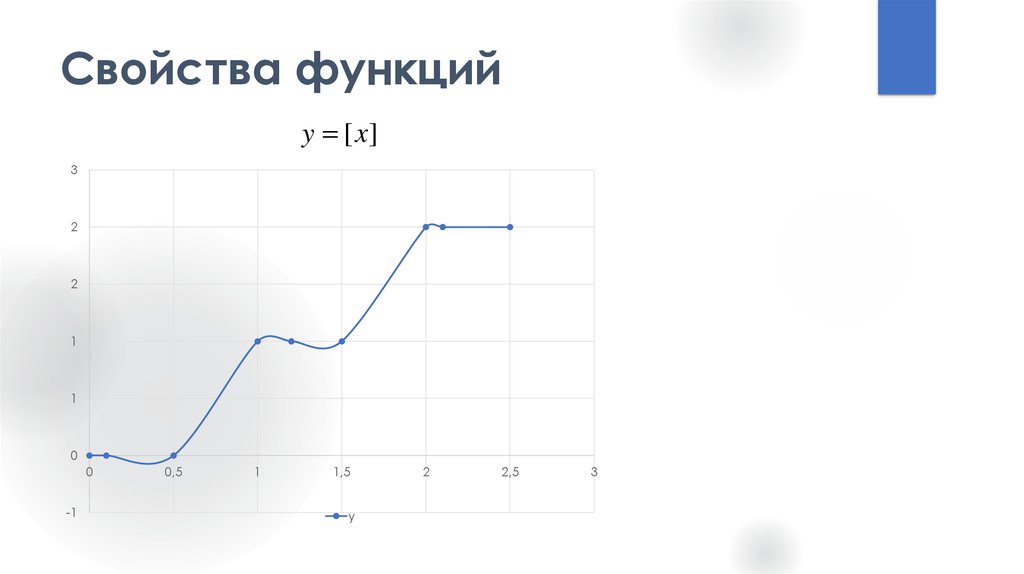
y [x]

11. Свойства функций

y [x]
3
2
2
1
1
0
0
-1
0,5
1
1,5
y
2
2,5
3

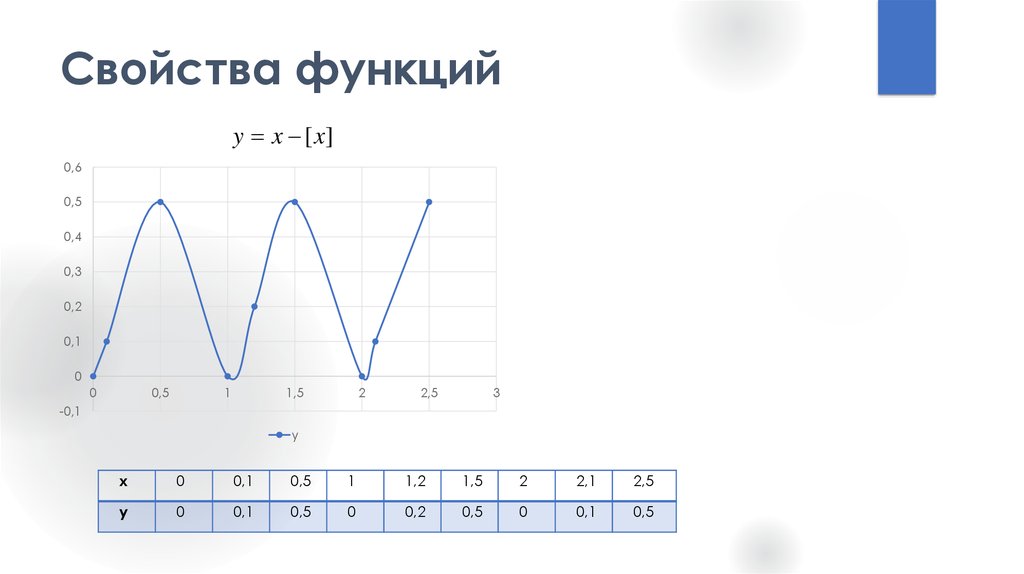
12. Свойства функций

y x [x]
0,6
0,5
0,4
0,3
0,2
0,1
0
0
0,5
1
1,5
2
2,5
3
-0,1
y
x
0
0,1
0,5
1
1,2
1,5
2
2,1
2,5
y
0
0,1
0,5
0
0,2
0,5
0
0,1
0,5

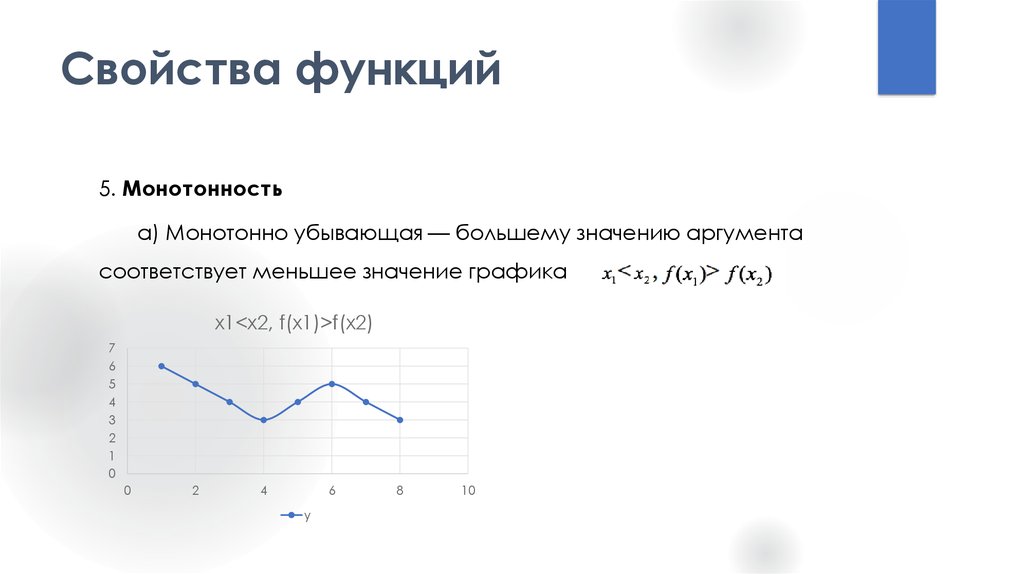
13. Свойства функций

5. Монотонность
а) Монотонно убывающая — большему значению аргумента
соответствует меньшее значение графика
x1<x2, f(x1)>f(x2)
7
6
5
4
3
2
1
0
0
2
4
6
y
8
10

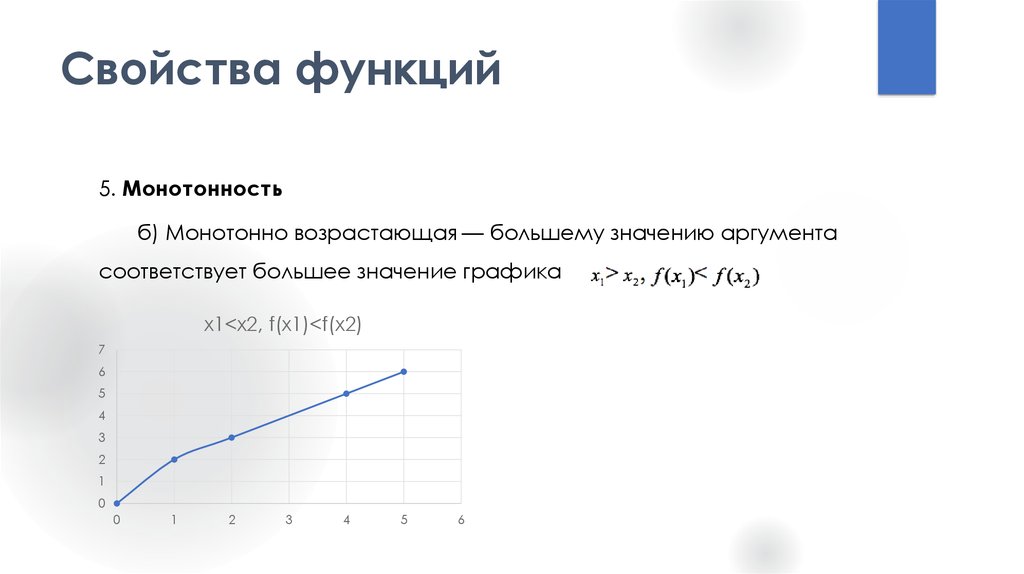
14. Свойства функций

5. Монотонность
б) Монотонно возрастающая — большему значению аргумента
соответствует большее значение графика
x1<x2, f(x1)<f(x2)
7
6
5
4
3
2
1
0
0
1
2
3
4
5
6

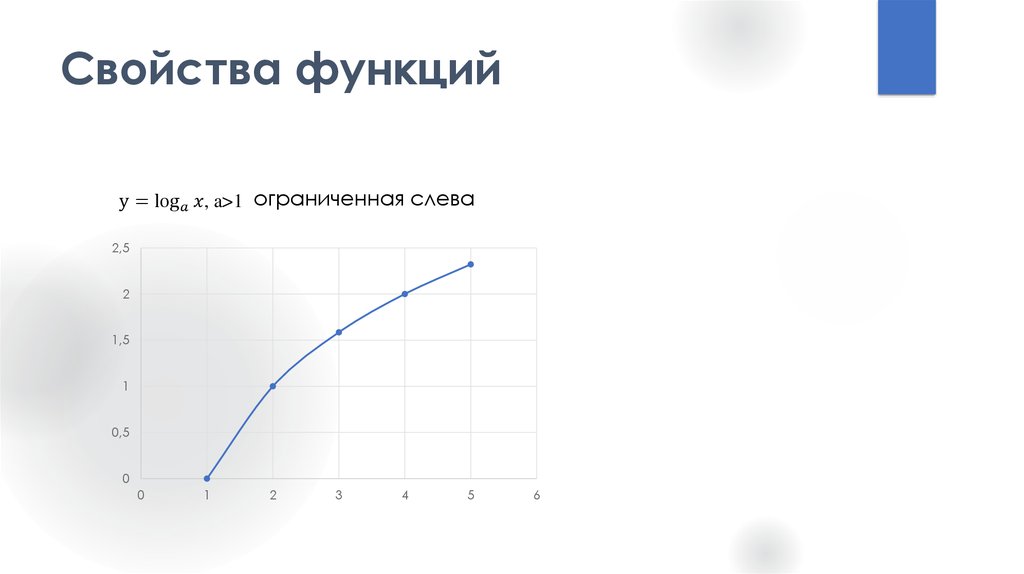
15. Свойства функций

6. Ограниченность — если существует такое число M из области
действительных чисел, что для всех x выполняется неравенство:
f ( x) M
сверху
f ( x) M
снизу
M 1 f ( x) M 2
x>M
x<M
и сверху, и снизу
слева
справа
M1 x M 2
и слева, и справа

16. Свойства функций

y = log