Similar presentations:
Добротность открытых оптических резонаторов
1. Оптоэлектронные и квантовые приборы и устройства Лекция 7: Добротность открытых оптических резонаторов
В.М. ШандаровТомский государственный университет
систем управления и радиоэлектроники
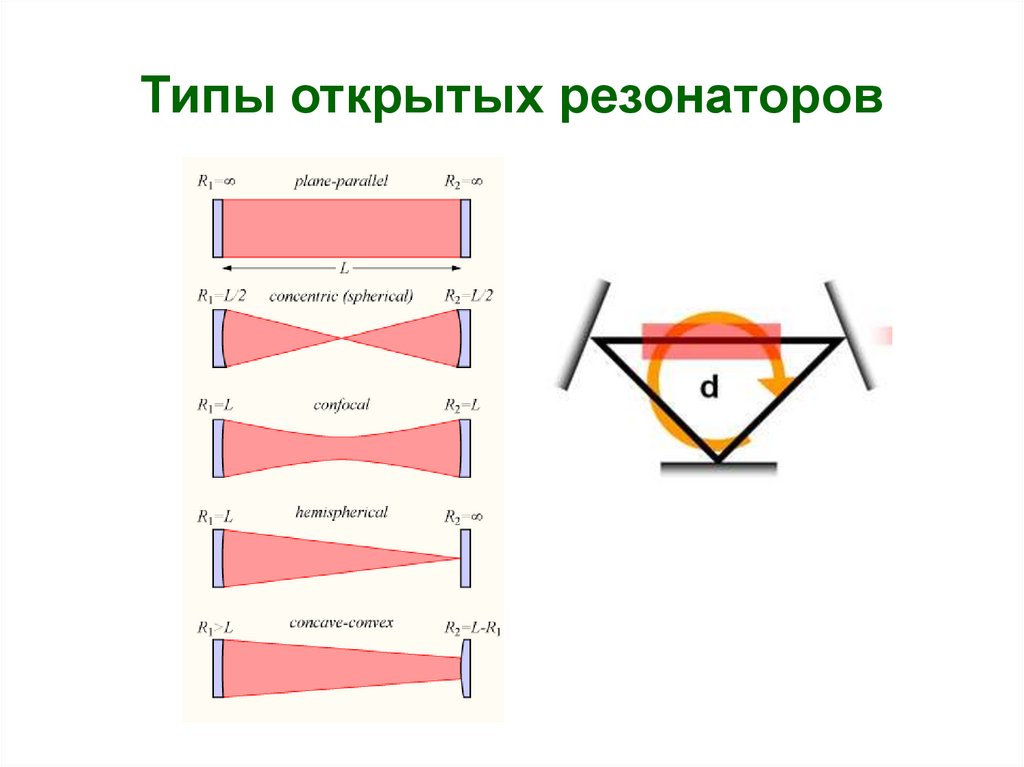
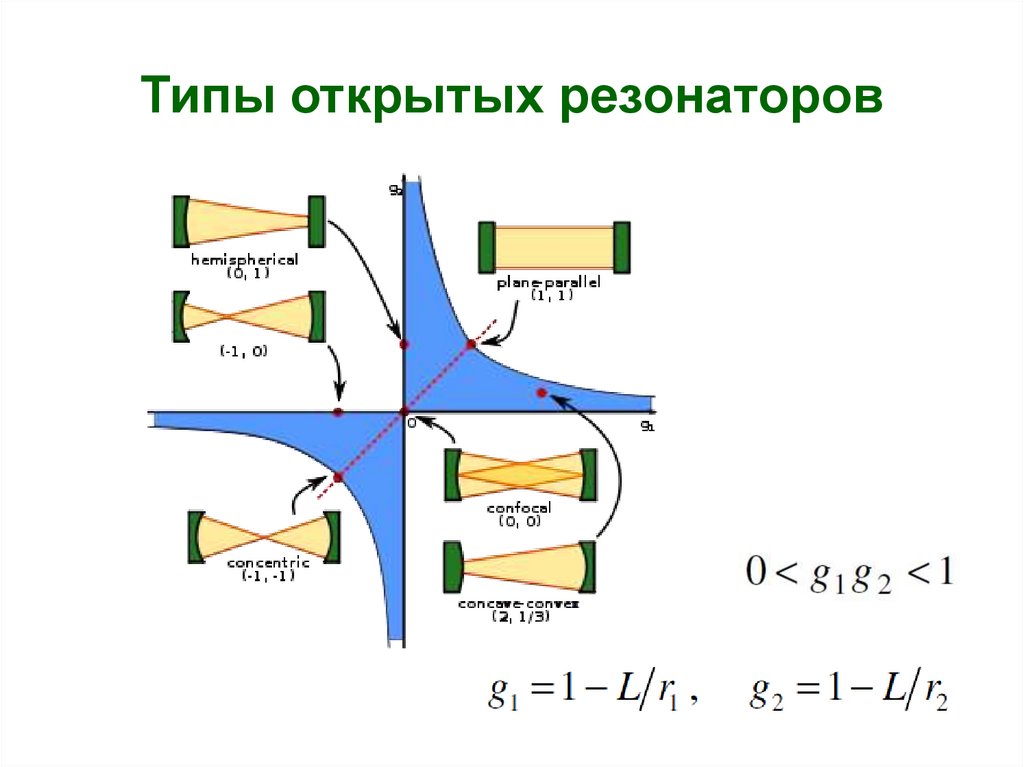
2. Типы открытых резонаторов
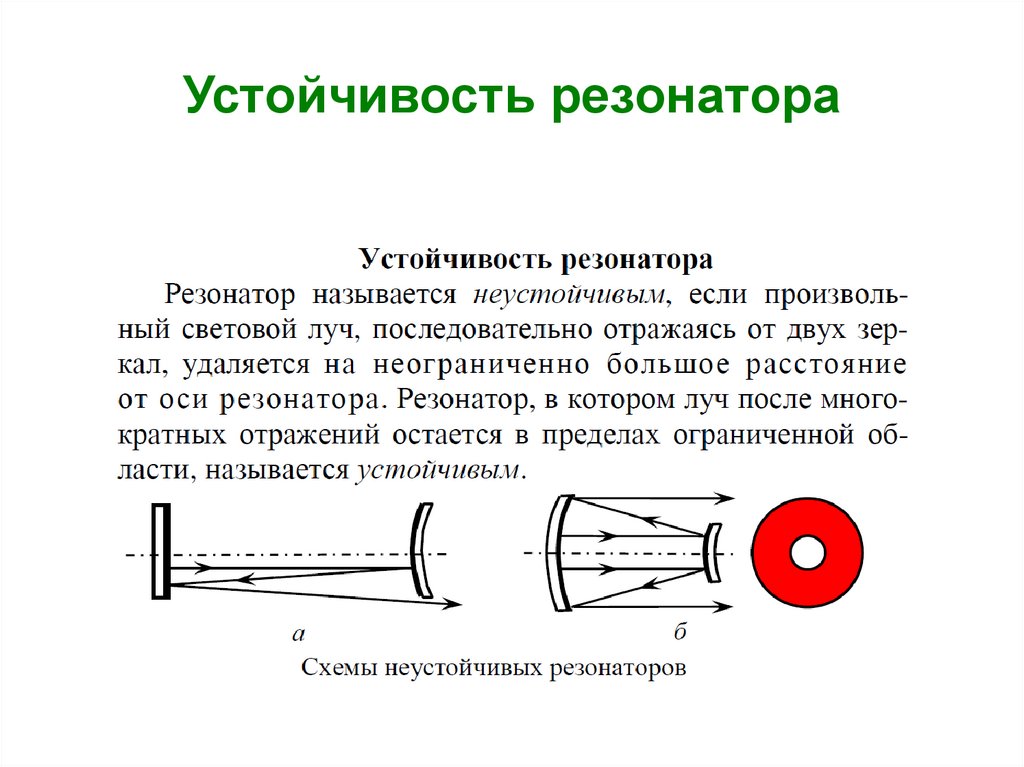
3. Устойчивость резонатора
4. Типы открытых резонаторов
5. Добротность типов колебаний открытого резонатора
Добротность резонаторов для данного типаколебаний определяется в общем виде как
отношение запасенной в нем энергии к энергии
потерь за период, умноженное на 2p:
6. Добротность типов колебаний открытого резонатора
В открытых резонаторах запасенная энергия убываетза счет:
-потерь на излучение, определяемых конечным
значением коэффициента прозрачности зеркал;
-точности юстировки, т.е. установки параллельности
зеркал в резонаторе с плоскопараллельными
зеркалами или расстояния между зеркалами и
совмещения оптических осей зеркал - в
-резонаторах со сферическими зеркалами;
- дифракционных потерь, т.е. потерь обусловленных
конечным значением размеров зеркал.
7. Добротность типов колебаний открытого резонатора
Рассмотрим влияние на добротность резонатора потерь,обусловленных отличием от единицы коэффициента
отражения зеркал.
Пусть Q добротность типа колебаний резонатора; Uтк
энергия, запасенная в типе колебаний; а его
собственная частота.
0
U тк U тк
exp( t )
Q
где Uтк0 начальная энергия, запасенная в типе колебаний
8. Добротность типов колебаний открытого резонатора
Величина изменения энергии типа колебаний за время dt:dU тк
0
U тк exp( t )dt U тк dt
Q
Q
Q
Найдем добротность типа колебаний за счет выхода энергии
через зеркала с коэффициентом отражения rотр
(коэффициент пропускания 1 rотр). Поглощением в
зеркалах пренебрегаем. Уменьшение энергии типа колебаний
при однократном отражении для волны с энергией Uтк /2:
U тк
U тк
( 1 rотр )
2
9. Добротность типов колебаний открытого резонатора
Эта энергия теряется за время прохода волны черезL
резонатор, период времени
t
c
и в среднем за единицу времени волна теряет энергию:
U òê(t 1)
U òê (1 rîòð )
2 t
Мода (тип колебаний) образуется
двумя волнами, бегущими
навстречу, поэтому энергия,
теряемая типом колебаний в U тк
единицу времени, в два раза
больше:
U òê (1 rîòð ) c
2L
U тк ( 1 rотр )
L
c
10. Добротность типов колебаний открытого резонатора
А энергия, теряемая типом колебания за время dt:dU тк
U тк ( 1 rотр )
L
c dt
Сравним это соотношение с полученным из общего
определения добротности:
dU òê
U òê (1 rîòð )
U òê dt
c dt
Q
L
11. Добротность типов колебаний открытого резонатора
Отсюда получим:L
2p L
Q
( 1 rотр )c ( 1 rотр )
Пример:
L=30 см: =0,6 мкм: rотр=0,9
Подставляя эти параметры в выражение для Q, получим:
2p 30
7
Q
3
10
0,6 10 4 0,1
Это существенно выше, чем добротность объемных
резонаторов в радиодиапазоне.
12. Условия самовозбуждения лазера
Условия самовозбуждения лазера, как и любогодругого генератора, включают в себя условия
баланса фаз и баланса амплитуд (мощностей).
Резонатор заполнен активной
средой.
Пусть R1 и R2 – комплексные
коэффициенты
отражения зеркал, а L – его длина.
У зеркала 1 возникает спонтанное
излучение, в виде плоской волны А1
оно распространяется в
направлении к зеркалу 2.
13. Условия самовозбуждения лазера
У зеркала 2 это поле будет иметь вид:A2 A1 exp a L exp L exp ikL
a - коэффициент усиления; - коэффициент потерь в
активной среде, обусловленных рассянием света на
неоднородностях; k – волновое число
поле отраженной волны A2 принимает вид:
A2 A1 R 2 1 exp a L exp L exp ikL
где ξ - коэффициент, учитывающий дифракционные потери
при отражении от зеркала
14. Условия самовозбуждения лазера
При обратном проходе к зеркалу 1 световое поле сноваусиливается и после отражения от него имеет вид:
2
A1 A1 R1 R2 1 exp 2 a L exp 2 L exp 2ikL
Для получения стационарных колебаний (или стоячей
волны в резонаторе) должно выполняться условие:
A1 A1
отсюда получаем:
2
R1 R2 1 exp 2 a L exp 2 L exp 2ikL 1
15. Условия самовозбуждения лазера
iR R e
k 2p
2p
2
R1 R2 1 exp 2 a L exp i 1 2 2 L 1
Отсюда получим уравнение баланса амплитуд:
2
R1 R 2 1 exp 2 a L 1
и баланса фаз:
2p
2 L 2p m
16. Условия самовозбуждения лазера
Уравнение баланса фаз означает наличие конструктивнойинтерференции, т.е. положительной обратной связи в
резонаторе.
Оно определяет частоту лазерного излучения и
выполняется на любой резонансной частоте открытого
резонатора.
Следовательно, на каждой из этих частот может быть
достигнута генерация, если выполняется условие баланса
амплитуд.
17. Условия самовозбуждения лазера
Колебания в резонаторе не будут затухать, если усиление вактивной среде компенсирует все потери в резонаторе.
Логарифмируя выражение для баланса амплитуд, получим:
2
R 1 R 2 1 exp 2 a L 1
L 2 L ln R R
1
ln R1 R2 1 2 a L 0
2 a
2
1
2
1
2
a
ln R1 R2 1
2L
2
18. Условия самовозбуждения лазера
11
a ln
2
L
R1 R2 1
Первое слагаемое справа характеризует потери в
активной среде, а второе – потери в зеркалах
Величина слева представляет собой пороговый
коэффициент усиления. Генерация возможна, когда
a>
19.
Спасибо завнимание!
















 electronics
electronics