ГИА. Открытый банк заданий по математике. Задача

1.

ГИА
Открытый банк заданий
по математике.
Задача

2.

Задание 14
(№ 206198)
Каким уравнением задается прямая,
проходящая через точки A(2; -5) и B(14; 1) ?
1
x y 7
Подсказка
2
2x y 9
Подсказка
3
x 2 y 12
Подсказка
4
x y 15
Подсказка

3.

Подсказка
1
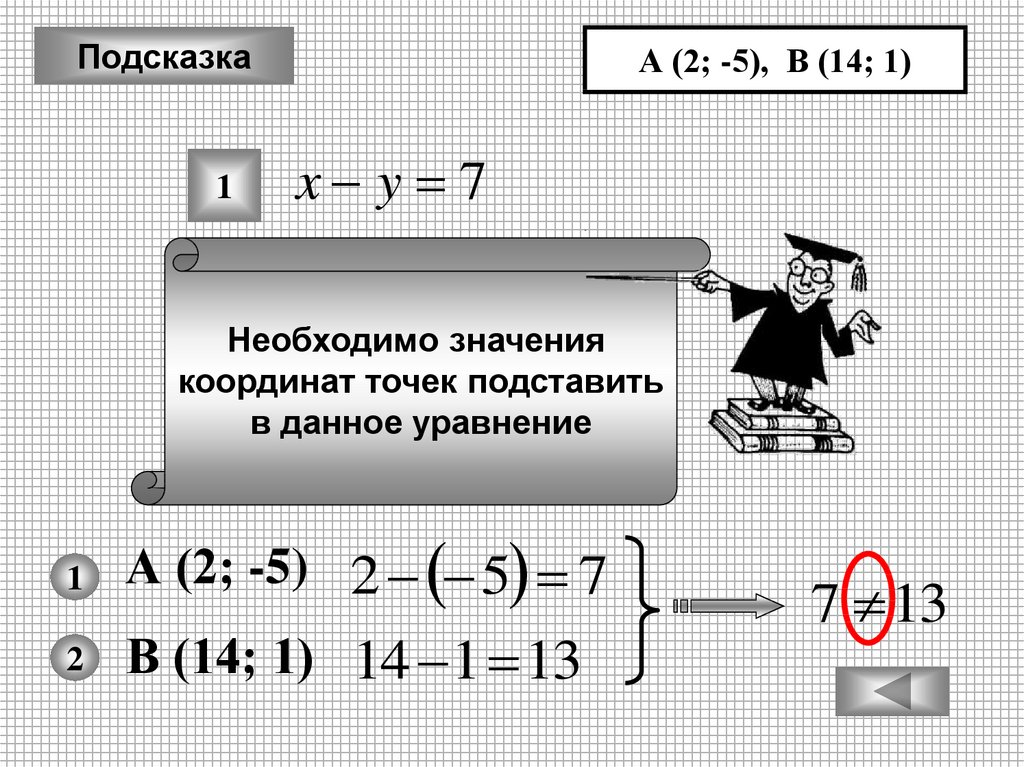
А (2; -5), В (14; 1)
x y 7
Необходимо значения
координат точек подставить
в данное уравнение
1
А (2; -5) 2 5 7
2
В (14; 1) 14 1 13
7 13

4.

Подсказка
А (2; -5), В (14; 1)
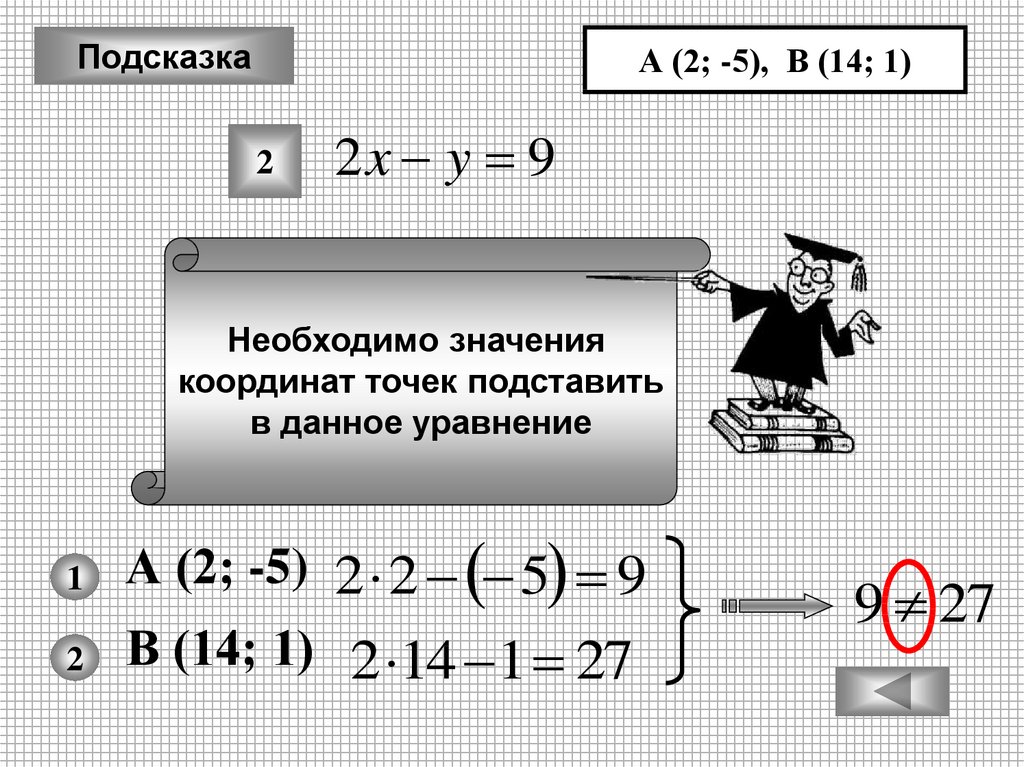
2
2x y 9
Необходимо значения
координат точек подставить
в данное уравнение
1
2
А (2; -5) 2 2 5 9
В (14; 1) 2 14 1 27
9 27

5.

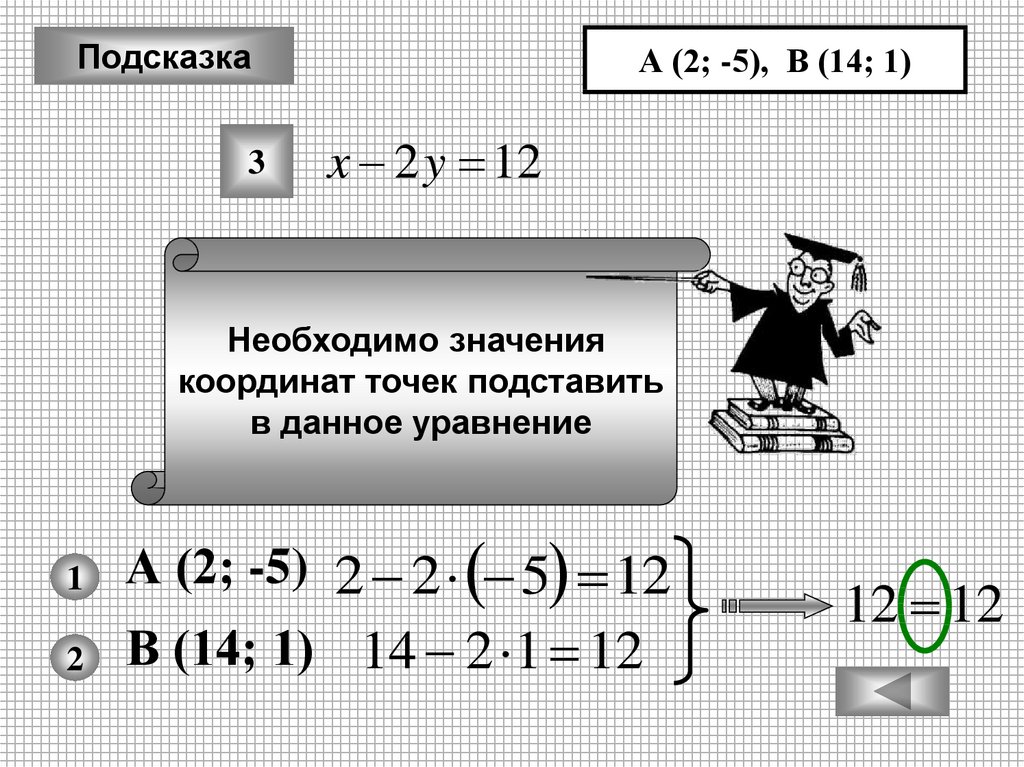
Подсказка
3
А (2; -5), В (14; 1)
x 2 y 12
Необходимо значения
координат точек подставить
в данное уравнение
1
2
А (2; -5) 2 2 5 12
В (14; 1) 14 2 1 12
12 12

6.

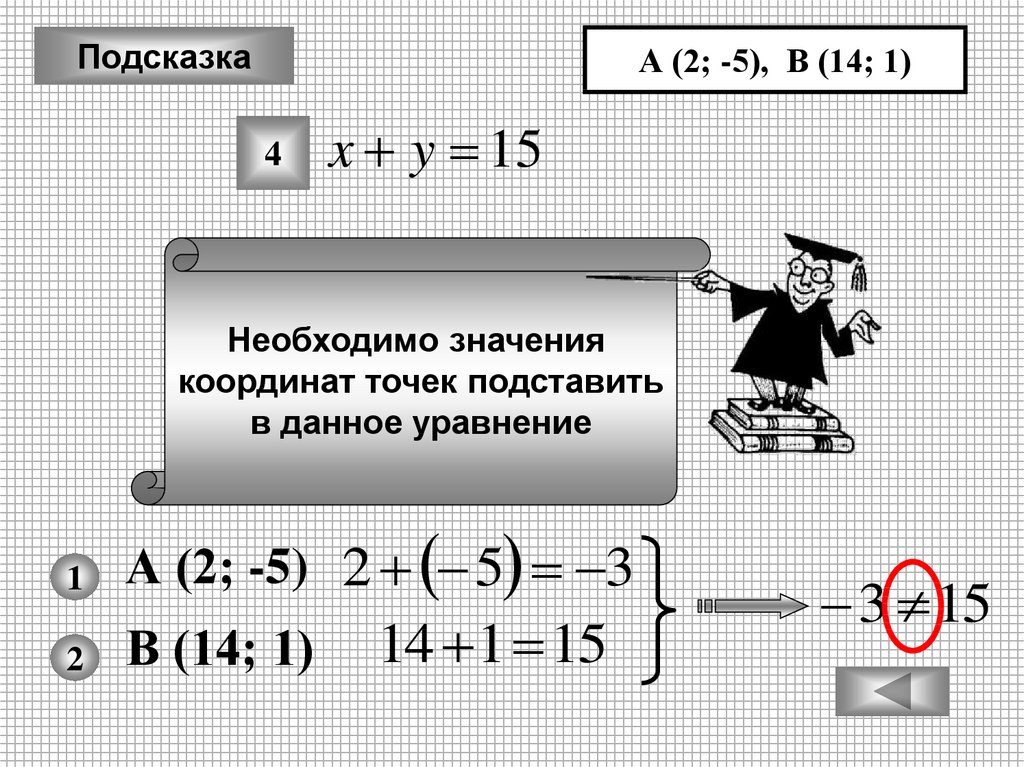
Подсказка
А (2; -5), В (14; 1)
4
x y 15
Необходимо значения
координат точек подставить
в данное уравнение
1
А (2; -5) 2 5 3
2
В (14; 1)
14 1 15
3 15

7.

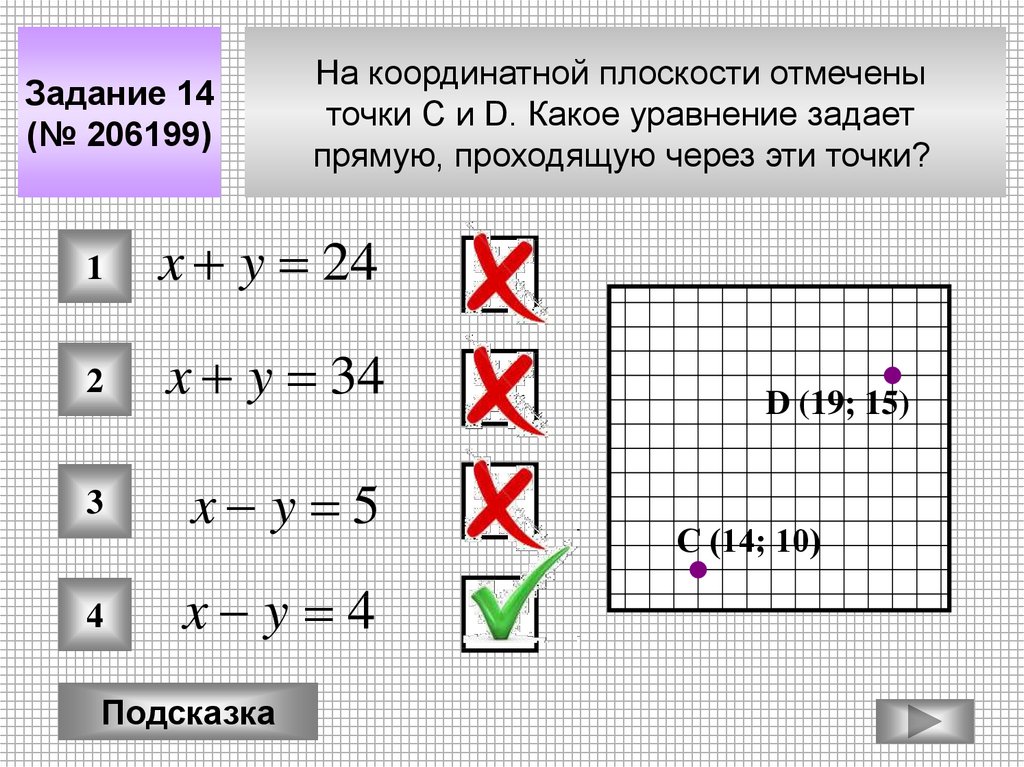
Задание 14
(№ 206199)
На координатной плоскости отмечены
точки C и D. Какое уравнение задает
прямую, проходящую через эти точки?
1
x y 24
2
x y 34
3
x y 5
4
x y 4
Подсказка
D (19; 15)
С (14; 10)

8.

y kx b
Подсказка
С (14; 10), D (19; 15)
Для нахождения значений
k и b подставим координаты
точек в уравнение линейной
функции.
Получим систему:
10 k 14 b
15 k 19 b
у x 4
k 1
b 4
x y 4

9.

Задание 14
(№ 208533)
На координатной плоскости отмечены
точки C и D. Какое уравнение задает
прямую, проходящую через эти точки?
Подсказка (3)
y kx b
10 k 10 b
11 k 6 b
D y(-10;
-10)
0,25 х 12,5
С (-6; -11)
k 0,25
b 12,5
Ответ:
y 0,25 х 12,5

10.

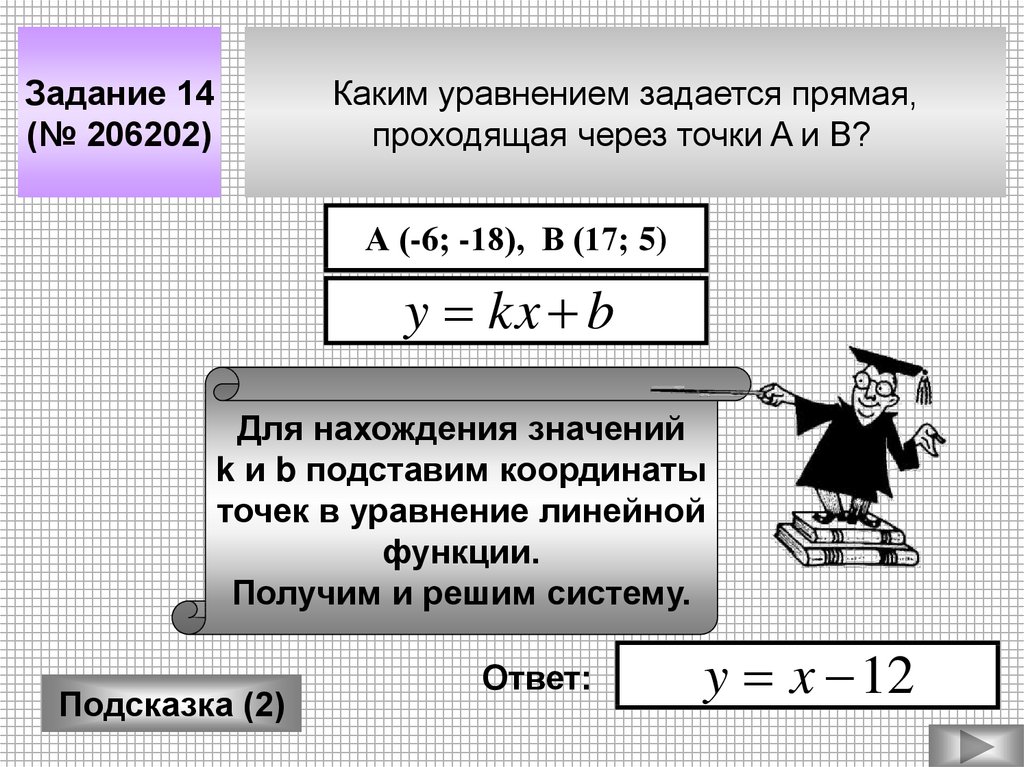
Задание 14
(№ 206202)
Каким уравнением задается прямая,
проходящая через точки A и B?
А (-6; -18), В (17; 5)
y kx b
Для нахождения значений
k и b подставим координаты
точек в уравнение линейной
функции.
Получим и решим систему.
Подсказка (2)
Ответ:
y x 12

11.

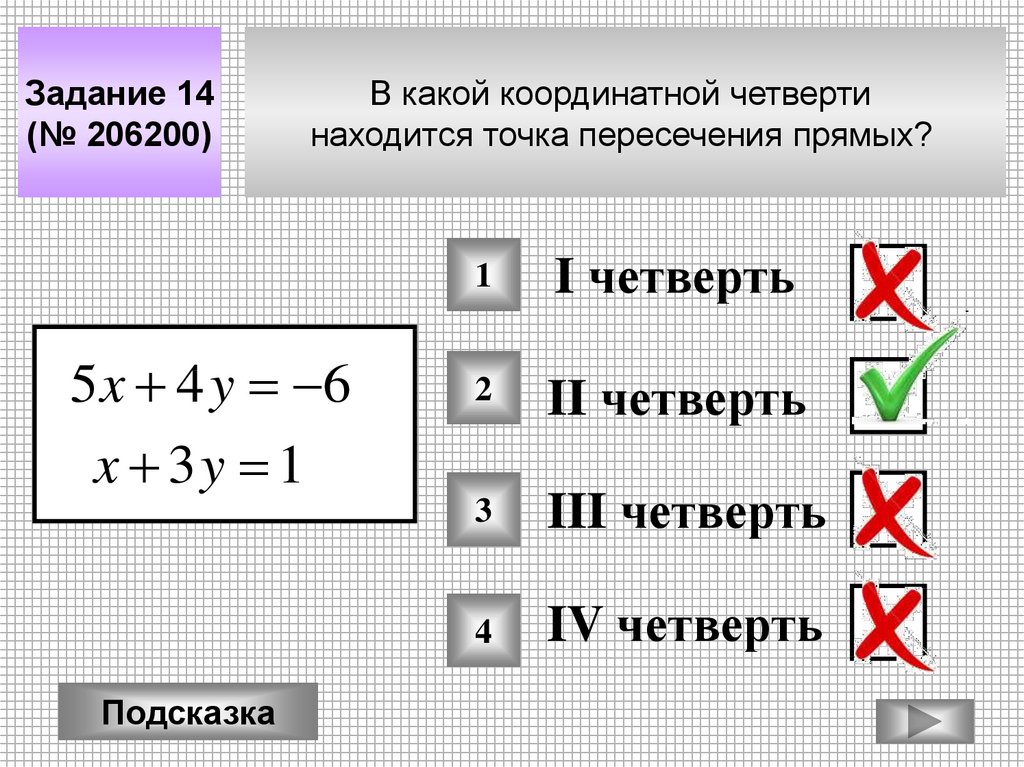
Задание 14
(№ 206200)
В какой координатной четверти
находится точка пересечения прямых?
5 x 4 y 6
x 3y 1
Подсказка
1
I четверть
2
II четверть
3
III четверть
4
IV четверть

12.

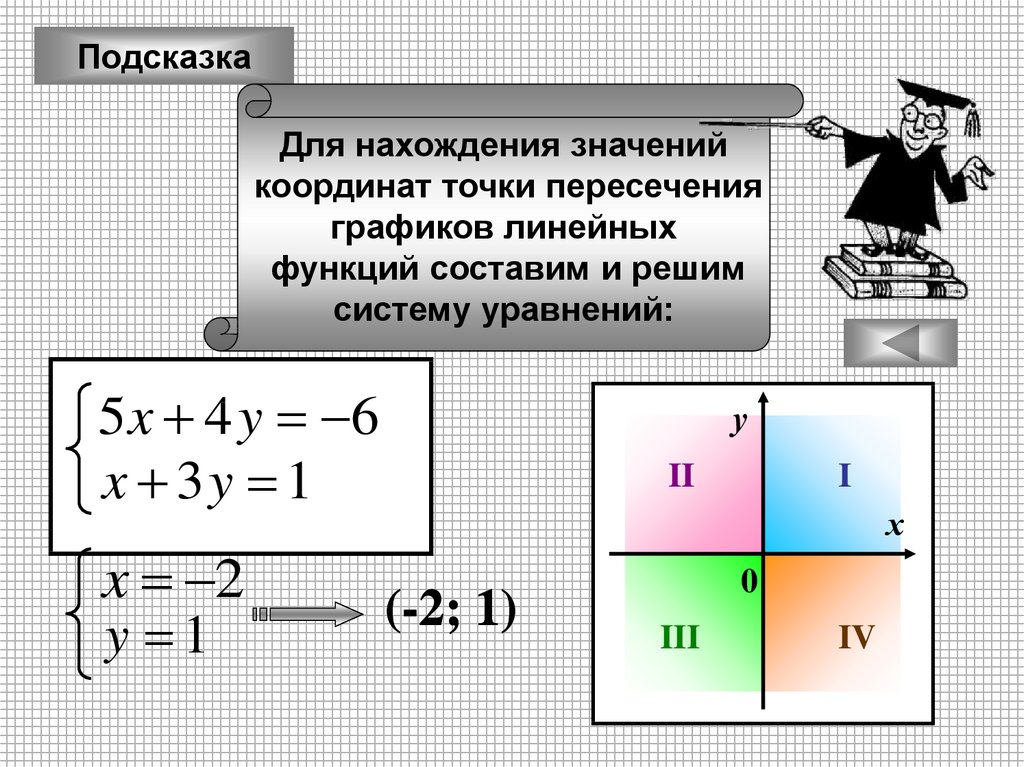
Подсказка
Для нахождения значений
координат точки пересечения
графиков линейных
функций составим и решим
систему уравнений:
5 x 4 y 6
x 3y 1
x 2
y 1
у
II
I
х
(-2; 1)
0
III
IV

13.

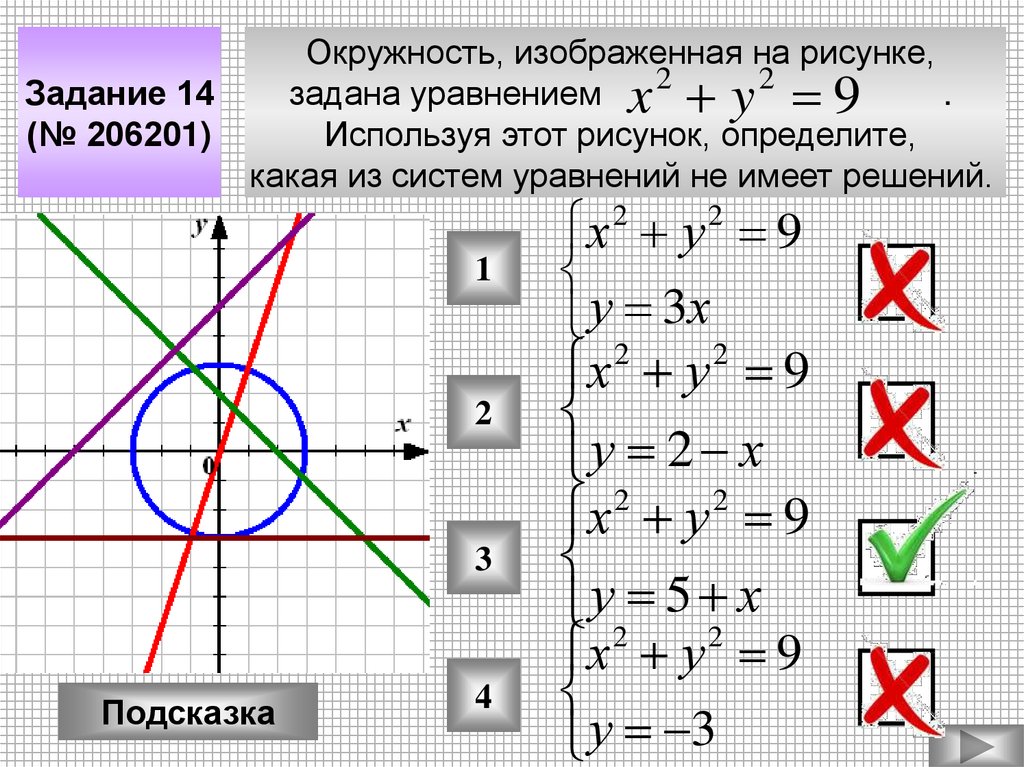
Задание 14
(№ 206201)
Окружность, изображенная на рисунке,
задана уравнением x 2 y 2 9
.
Используя этот рисунок, определите,
какая из систем уравнений не имеет решений.
х у 9
у 3х
х 2 у 2 9
у 2 х
2
2
х у 9
у2 5 2 х
х у 9
у 3
2
1
2
3
Подсказка
4
2

14.

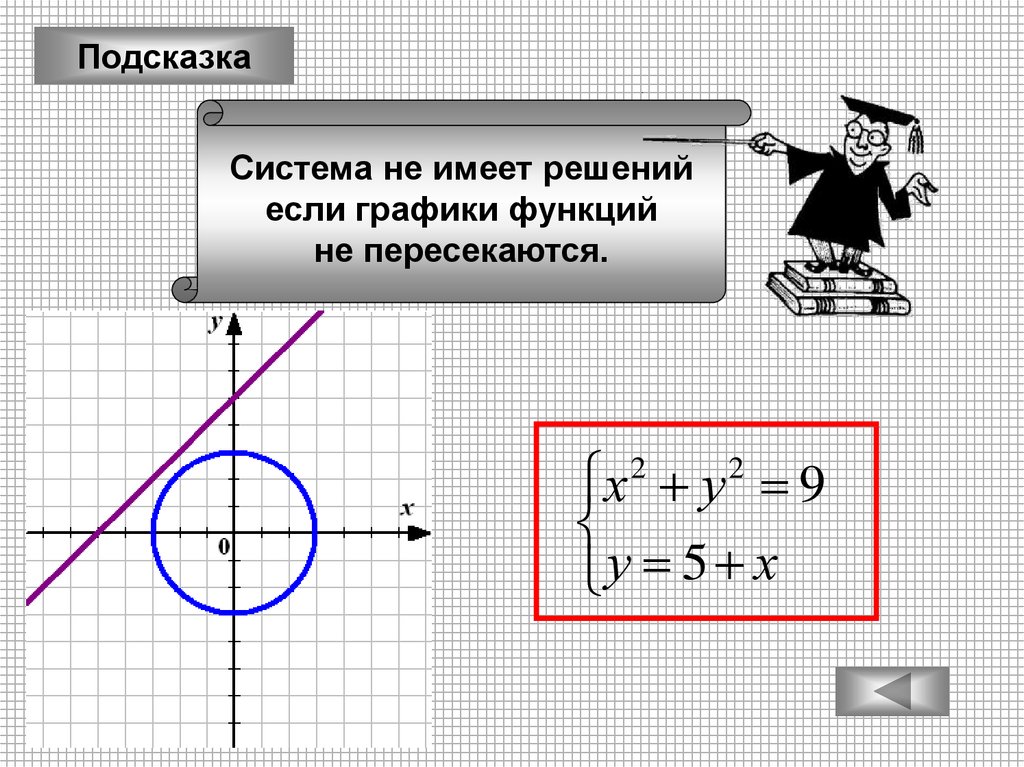
Подсказка
Система не имеет решений
если графики функций
не пересекаются.
х у 9
у 5 х
2
2

15.

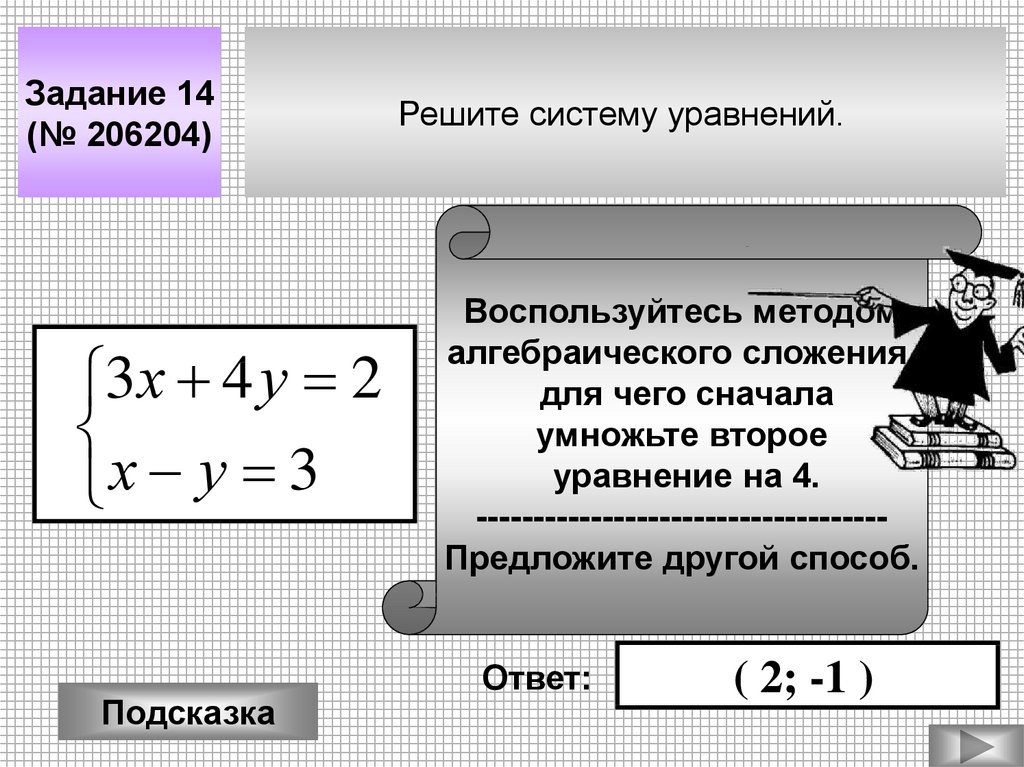
Задание 14
(№ 206204)
3х 4 у 2
х у 3
Подсказка
Решите систему уравнений.
Воспользуйтесь методом
алгебраического сложения,
для чего сначала
умножьте второе
уравнение на 4.
-----------------------------------Предложите другой способ.
Ответ:
( 2; -1 )

16.

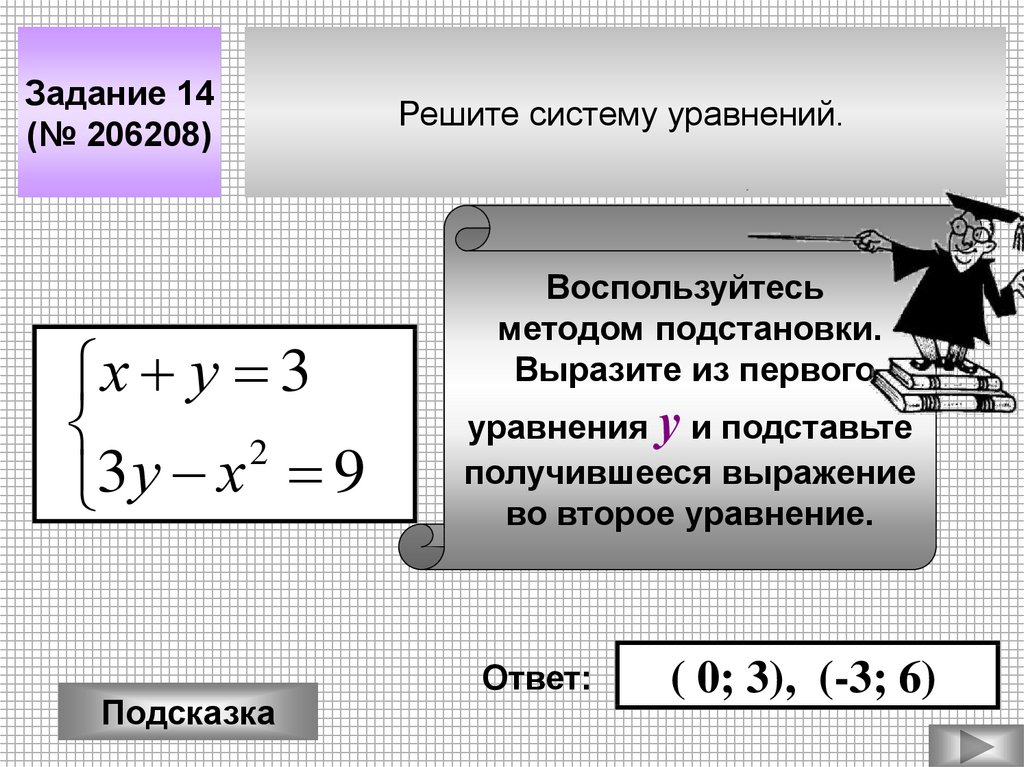
Задание 14
(№ 206208)
х у 3
2
3 у х 9
Подсказка
Решите систему уравнений.
Воспользуйтесь
методом подстановки.
Выразите из первого
уравнения у и подставьте
получившееся выражение
во второе уравнение.
Ответ:
( 0; 3), (-3; 6)

17.

Задание 14
(№ 206209)
Вычислите координаты точек пересечения
параболы и прямой.
у х 5х
2
у х 16
Подсказка (3)
х 5 х х 16
2
х1 8; х2 2
у1 24; у2 14
Ответ:
( 8; 24), (-2; 14)

18.

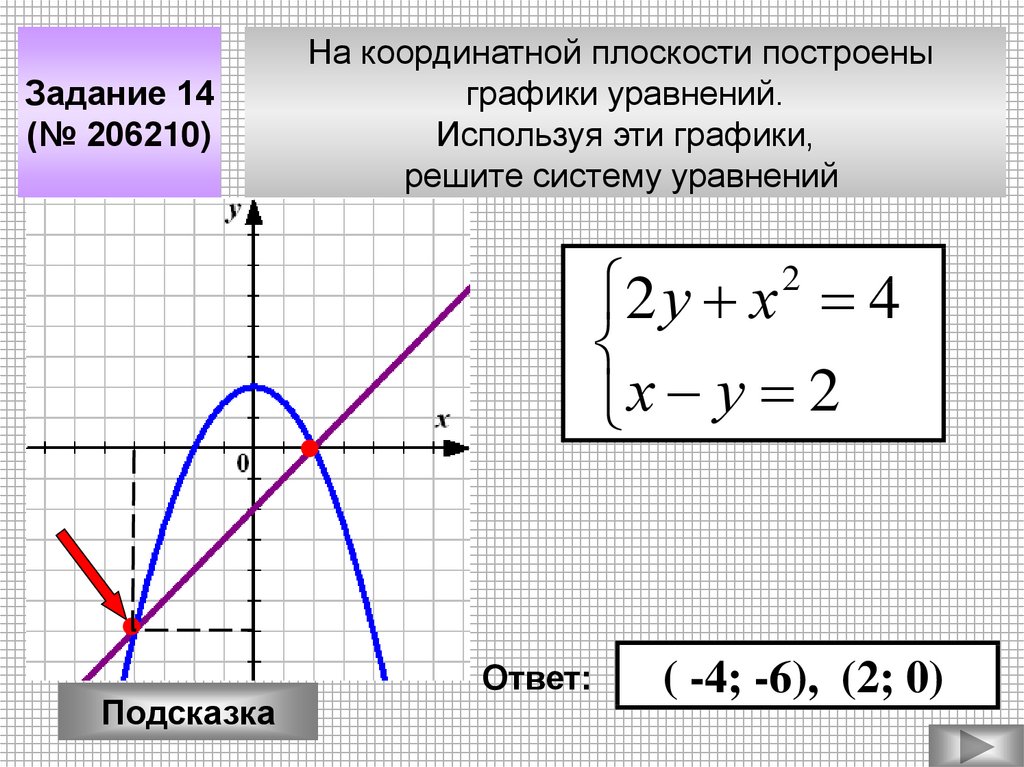
Задание 14
(№ 206210)
На координатной плоскости построены
графики уравнений.
Используя эти графики,
решите систему уравнений
2 у х 4
х у 2
2
Подсказка
Ответ:
( -4; -6), (2; 0)

19.

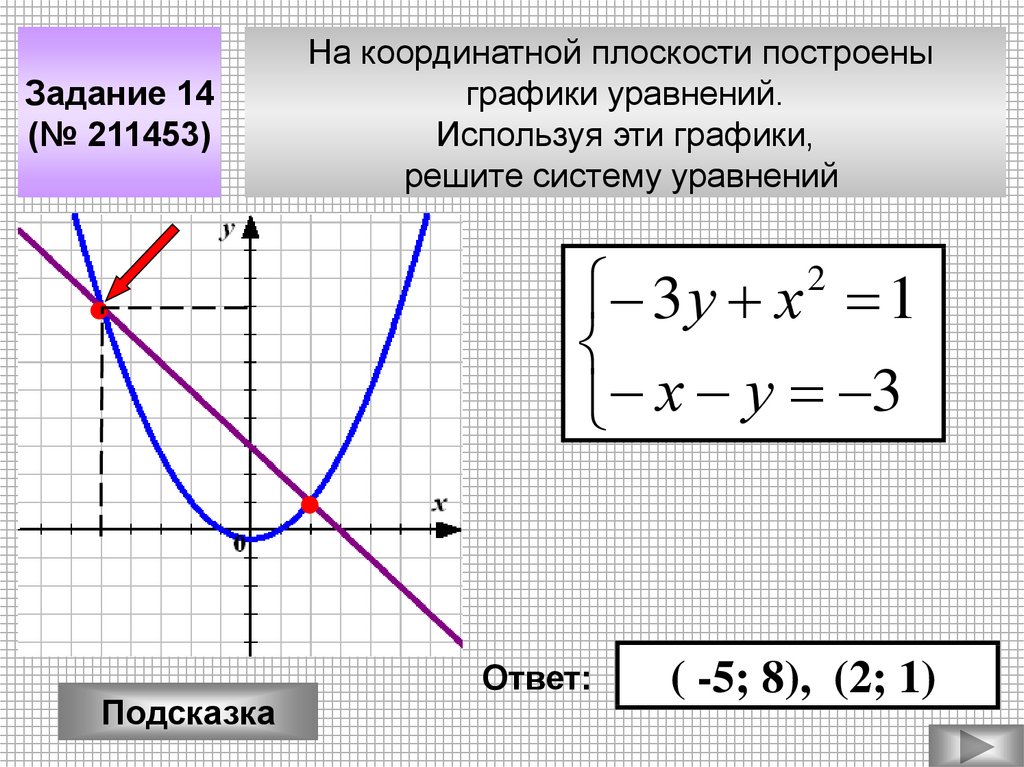
Задание 14
(№ 211453)
На координатной плоскости построены
графики уравнений.
Используя эти графики,
решите систему уравнений
3 у х 1
х у 3
2
Подсказка
Ответ:
( -5; 8), (2; 1)

20.

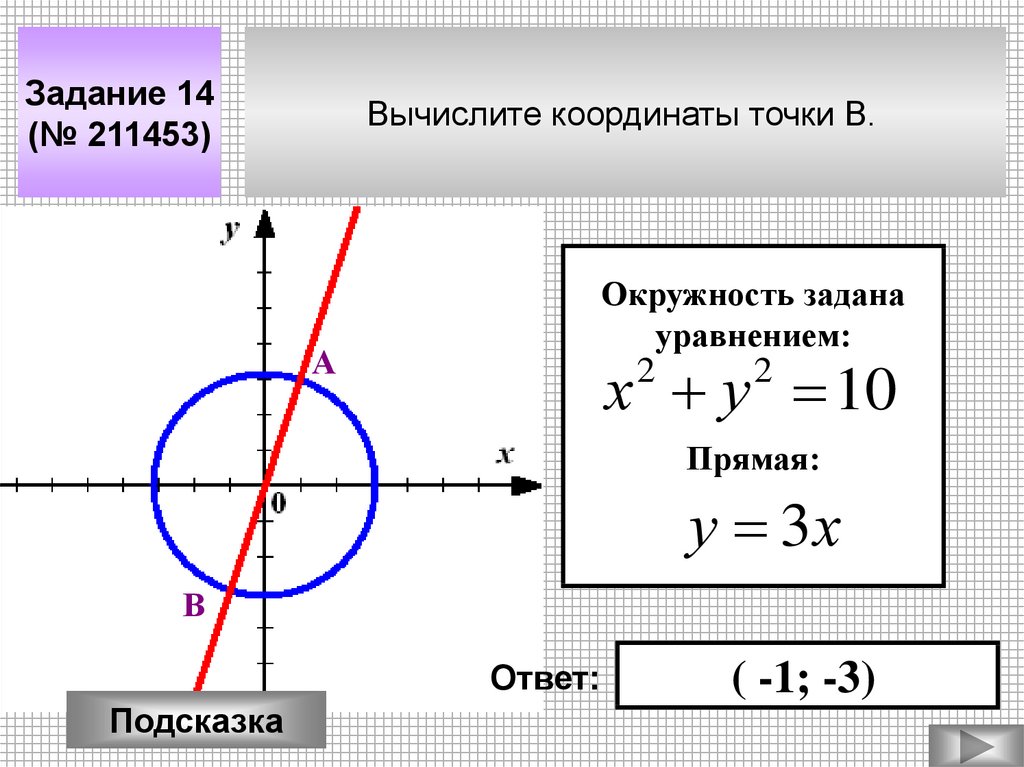
Задание 14
(№ 211453)
Вычислите координаты точки В.
Окружность задана
уравнением:
2
2
А
х у 10
Прямая:
у 3х
В
Ответ:
Подсказка
( -1; -3)

21.

Подсказка
Найдём координаты точек
пересечения графиков
функций.
х у 10
у 3х
2
А
2
х1 1; х2 1
у1 3; у2 3
III
В

22.

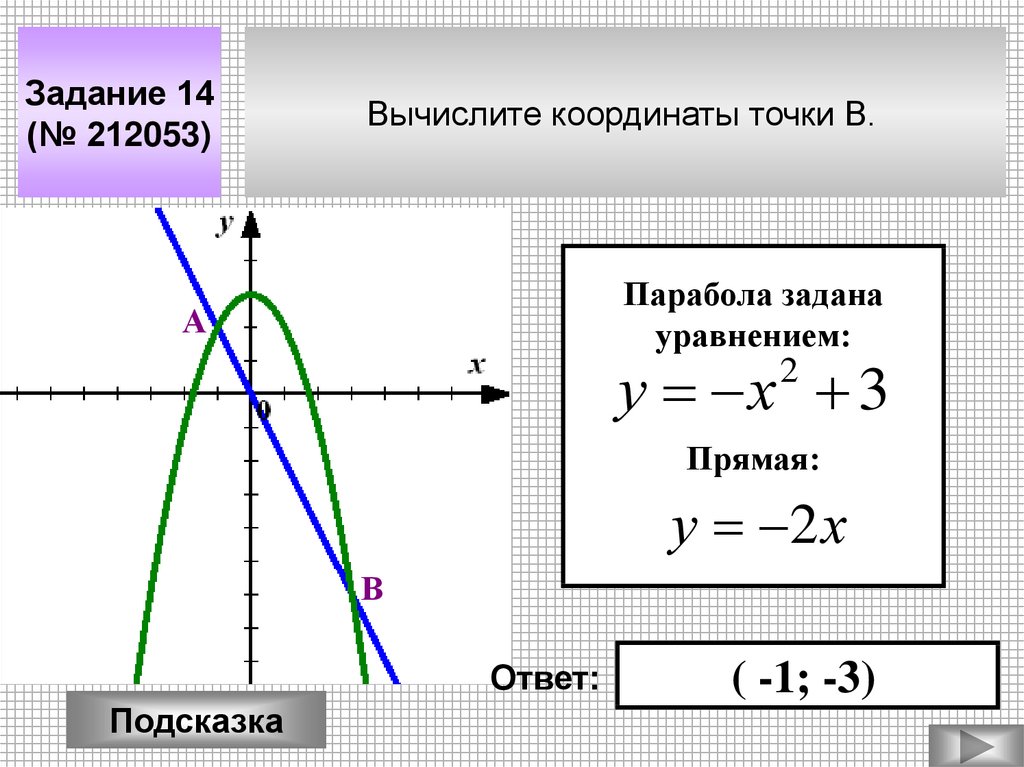
Задание 14
(№ 212053)
Вычислите координаты точки В.
А
Парабола задана
уравнением:
2
у х 3
Прямая:
у 2 х
В
Ответ:
Подсказка
( -1; -3)

23.

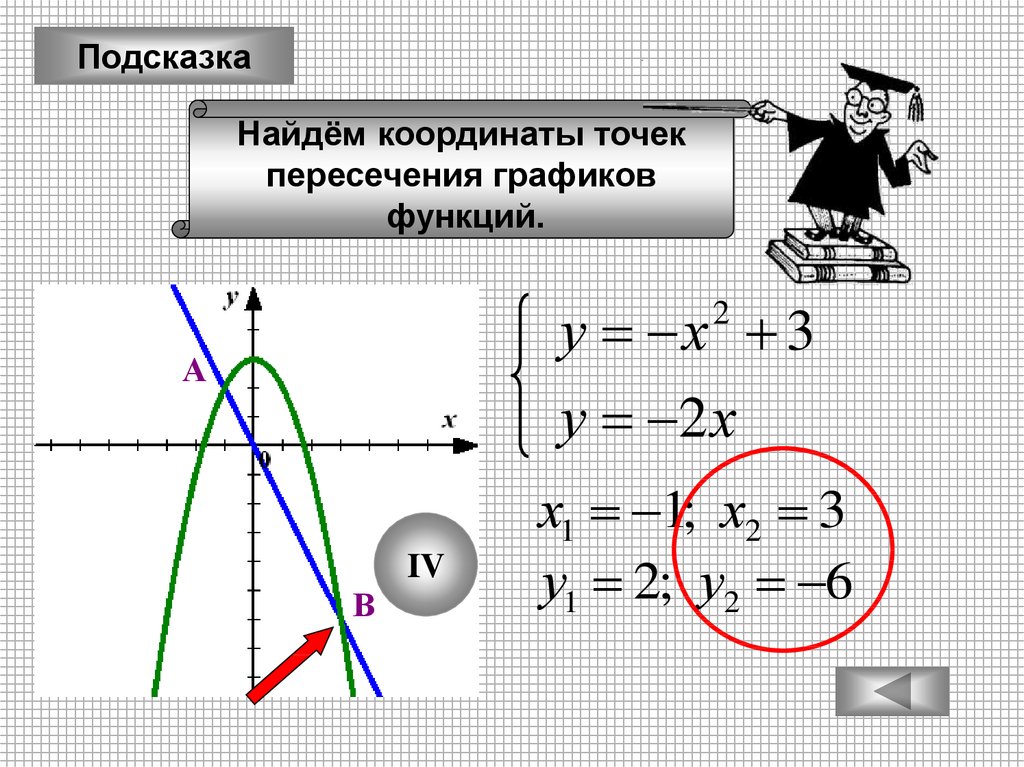
Подсказка
Найдём координаты точек
пересечения графиков
функций.
у х 3
у 2 х
2
А
IV
В
х1 1; х2 3
у1 2; у2 6

24.

При создании презентации были использованы
задачи с сайта
«Открытый банк заданий по математике»
ГИА – 2012.
http://www.mathgia.ru:8080/or/gia12/Main.html?view=Pos