Принцип суперпозиции полей

1. Принцип суперпозиции полей.

Взаимодействие электрических зарядов
в вакууме.
Напряженность электрического поля.

2. Свойства электрических зарядов

Физическая величина, определяющая
способность частиц участвовать в
электрическом взаимодействии,
называется электрическим зарядом
этой частицы. Электрический заряд –
это неотъемлемое свойство
элементарной частицы, и без нее сам
по себе заряд существовать не может.

3. Свойства электрических зарядов

К числу наиболее важных свойств
электрических зарядов относятся:
1. Существование двух видов электрических
зарядов («положительных» и
«отрицательных»), отличающихся друг от
друга лишь тем, что в любой системе зарядов
все заряды одного знака отталкиваются друг
от друга, а противоположные по знаку –
притягиваются.

4. Свойства электрических зарядов

2. Дискретность величины электрического
заряда. В природе существует минимальный
заряд, называемый элементарным и равный
по величине 1,6 10-19 Кл, а все заряды тел
кратны ему.
3. Аддиттивность. При соединении
нескольких заряженных тел полный заряд
оказывается равным алгебраической сумме
зарядов соединяемых тел.

5. Свойства электрических зарядов

4. Сохранение заряда. Согласно закону
сохранения заряда, в изолированной системе
полный заряд всех тел остается неизменным
при любых взаимодействиях тел, приводящих
к перераспределению зарядов между ними.
5. Инвариантность. Электрический заряд
остается неизменным при переходе от одной
системы отсчета к другой.

6. Закон Кулона

Взаимодействие заряженных тел
осуществляется посредством электрических
полей, образованных этими телами.
Взаимодействие точечных зарядов в вакууме
описывается законом Кулона:
q1q2
1
F = k0 2 , k0 =
4pe0
r

7. Закон Кулона

Точечным зарядом называется заряженное
тело, размеры которого пренебрежительно
малы по сравнению с расстоянием до других
заряженных тел, с которым оно
взаимодействует.
Таким образом, сила
взаимодействия точечных зарядов
в вакууме пропорциональна
величине зарядов и обратно
пропорциональна квадрату
расстояния между ними.

8. Закон Кулона

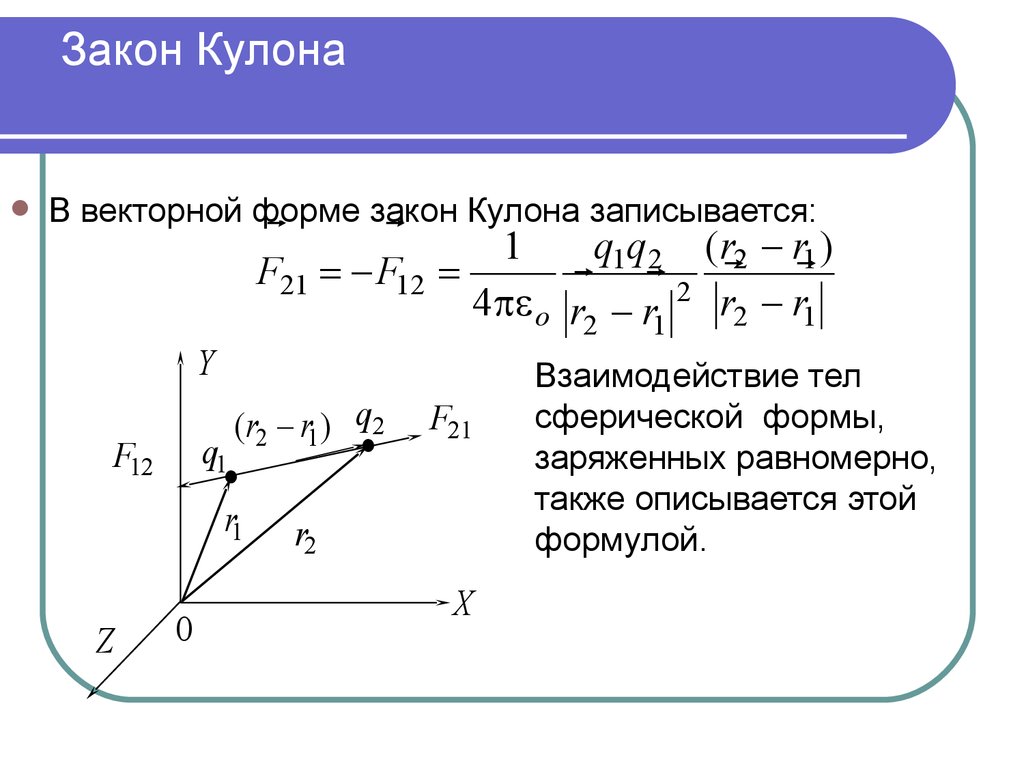
В векторной форме закон Кулона записывается:
F21 = F12 =
Y
q
(r2 r1 ) 2
q1
r1 r
F12
q1q2 (r2 r1 )
1
2
4pe o r2 r1 r2 r1
F21
2
Z
0
X
Взаимодействие тел
сферической формы,
заряженных равномерно,
также описывается этой
формулой.

9. Закон Кулона

F12 – сила, действующая на заряд q1 , со
где
стороны заряда q 2 .
F21 – сила, действующая на заряд q2 , со
стороны заряда q1 .
r2 r1
- единичный вектор, направленный
r2 r1
от заряда q1 к заряду q 2 .

10. Характеристики электрического поля. Напряженность.

Электрическим полем называется часть
пространства, в которой на помещенный
туда электрический заряд действуют
электрические силы.
Поле неподвижных зарядов является
стационарным и называется
электростатическим.
Основное свойство поля заключается в
том, что на всякий заряд, помещенный
в это поле, действует сила.

11. Силовая характеристика. Напряженность поля.

Силовой характеристикой поля,
создаваемого зарядом q , является
напряженность электростатического поля,
которая определяется отношением силы,
действующей на заряд q , к величине этого
заряда
E =
F
q

12. Напряженность поля.

Напряженность поля, созданного точечным
зарядом, легко получается из закона Кулона:
E (r ) =
Y
0
Z
q
r
r
E (r )
X
1
q
(r r )
4pe o r r 3

13. Напряженность поля. Принцип суперпозиции.

Поля, одновременно созданные в одной
и той же области различными
источниками, существуют независимо
друг от друга.
Напряженность поля, созданного системой
зарядов, определяется в каждой точке
пространства как геометрическая сумма
напряженностей полей отдельных зарядов –
принцип суперпозиции полей.

14. Принцип суперпозиции.

Для дискретного распределения
зарядов
n
E (r ) = E1 (r ) E 2 (r ) ... E n (r ) = Ei (r )
i =1
Для системы точечных зарядов
E (r ) =
1
4pe o
n
qi
3 (r ri )
i =1 r ri

15. Принцип суперпозиции

Когда заряд непрерывно распределен в
какой-либо области пространства, вводятся
понятия
dq
линейной плотности заряда =
d ,
dq
,
поверхностной плотности заряда =
ds
dq
и объемной плотности заряда =
.
dV

16. Принцип суперпозиции

Соответственно заряд элемента длины
d , поверхности ds и объема dV равен d ,
рассчитывается
ds, dV , а напряженность
d
по формулам: E (r ) = 1
(r r );
3
4pe o
r
r
( L)
1
ds
E (r ) =
(r r );
3
4pe o
r r
(S )
E (r ) =
1
4pe o
dV
3 (r r )
(V ) r r

17. Силовые линии (линии напряженности)

Поле может быть представлено графически с помощью
силовых линий (линий напряженности). Силовая линия –
это воображаемая линия, касательная к которой в любой
точке совпадает с вектором напряженности в этой точке.
Силовые линии проводятся так, чтобы их густота была
пропорциональна (или равна) значению напряженности
поля в данной точке пространства. Линии напряженности
электрического поля начинаются на положительных, а
заканчиваются на отрицательных зарядах или уходят в
бесконечность. Они непрерывны и нигде не пересекаются.

18. Пример 1

Рассмотрим применение принципа суперпозиции в
случае поля, созданного электрической системой из
двух одинаковых по модулю, но противоположных по
знаку зарядов с расстоянием между зарядами,
равным l в точке, лежащей на перпендикуляре,
восстановленном из середины отрезка,
соединяющего заряды

19. Пример 1

В соответствии с принципом суперпозиции
E = E E
Так как заряды равны по модулю и равноудалены
от точки А, то
E = E =
1
q
4pe 0 (r 2 l 2 )
4

20. Пример 1

Напряженность результирующего поля
E = 2 E cos ,
cos =
Окончательно
l
2
2
l
2 r
4
1
E=
4pe 0
ql
2 3
l
2
(r ) 2
4

21. Пример 2.

напряженность электрического поля в
Определим
точке А на расстоянии х от бесконечно длинного,
равномерно заряженного стержня.
Введем
линейную
,
плотность
тогда
1
dy
dE =
4pe 0 ( x 2 y 2 )

22. Пример 2.

1 cos dy
dE x = dE cos =
4pe 0 ( x 2 y 2 )
1 sin dy
dE y = dE sin =
4pe 0 ( x 2 y 2 )

23. Пример 2.

Проинтегрируем
Ex =
4pe 0
Ey =
4pe 0
cos dy
(x2 y2 )
sin dy
(x2 y 2 )
Произведем замену переменных
y = xtg ,
xd
dy =
,
2
cos
2
x
2
2
x y =
.
2
cos

24. Пример 2.

Результат интегрирования
p
2
2
Ex =
cos d =
4pe 0 x p
4pe 0 x
2
p
2
Ey =
sin d = 0
4pe 0 x p
2
E = Ex =
;
4pe 0 x
2
2
E=
i.
4pe 0 x