Similar presentations:
Непрерывность функции
1.
НЕПРЕРЫВНОСТЬФУНКЦИИ
1
2.
НЕПРЕРЫВНОСТЬ ФУНКЦИИ В ТОЧКЕФункция f(x) называется непрерывной в точке x0, если предел
функции и ее значение в этой точке равны, т.е.
lim f x f ( x0 )
x x0
Точка x0, называется точкой разрыва функции f(x), если функция
f(x) в точке x0 не является непрерывной.
2
3.
КЛАССИФИКАЦИЯ РАЗРЫВОВ ФУНКЦИИY
lim f x 5
5
x 0 0
3
X
lim f x 3
x 0 0
0
x 0 точка разрыва первого рода.
3
4.
КЛАССИФИКАЦИЯ РАЗРЫВОВ ФУНКЦИИ1
lim ;
x 0 x
1
lim .
x 0 x
4
5.
КЛАССИФИКАЦИЯ РАЗРЫВОВ ФУНКЦИИlim f x lim f x а f ( x0 )
x x0 0
x x0 0
5
6.
НЕПРЕРЫВНОСТЬ СЛОЖНОЙ ФУНКЦИИЕсли на некотором множестве Х определена функция g(x) с
множеством значений G, а на множестве G определена функция
f(g), то функция f(g(x)) называется сложной функцией.
Если функция g(x) непрерывна в точке x0, а функция f(g)
непрерывна в точке g0=g(x0), то функция f(g(x)) непрерывна в
точке x0.
6
7.
АСИМПТОТЫ ГРАФИКА ФУНКЦИИ7
8.
89.
Чтобы найти наклонную асимптоту графика функции y=f(x) следуетнайти пределы:
f x
lim
x
x
k
lim f x k x b
x
Если оба предела существуют и конечные, то прямая y=kx + b –
наклонная асимптота.
9
10.
Примеры.Исследовать на непрерывность функцию. Найти асимптоты графика
функции, если они существуют. Построить график функции.
1) y
2x 1
x 2
D y : ;2 2; x 2 точка разрыва.
2 x 1 2 2 0 1 3
;
x 2 0 x 2
2 0 2 0
lim
2 x 1 2 2 0 1 3
lim
x 2 0 x 2
2 0 2 0
x 2 точка разрыва второго рода,
прямая x 2 вертикальная асимптота .
10
11.
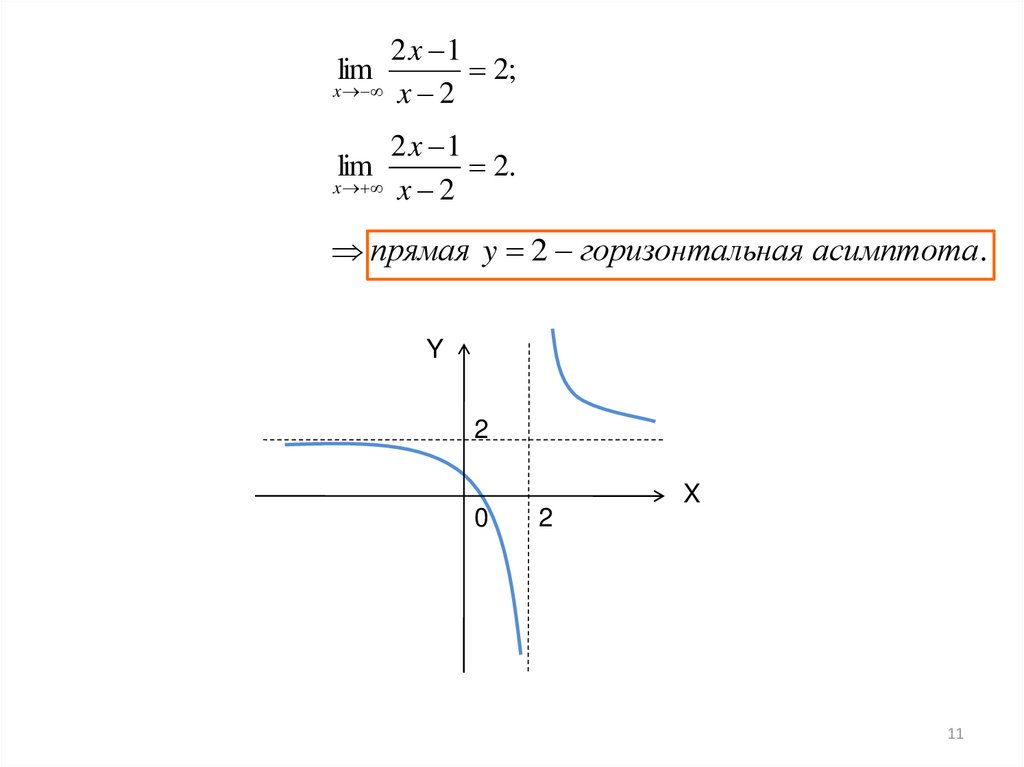
2x 1lim
2;
x x 2
2x 1
lim
2.
x x 2
прямая y 2 горизонтальная асимптота .
Y
2
X
0
2
11
12.
2) y 21
x 3
D y : ;3 3; x 3 точка разрыва.
lim 2
1
x 3
x 3 0
lim 2
x 3 0
1
x 3
1
(3 10) 3
1
1
0
2
2 2 0;
2
1
(3 10) 3
0
2
2 2 .
x 3 точка разрыва второго рода,
прямая x 3 вертикальная асимптота при x 3 0 .
12
13.
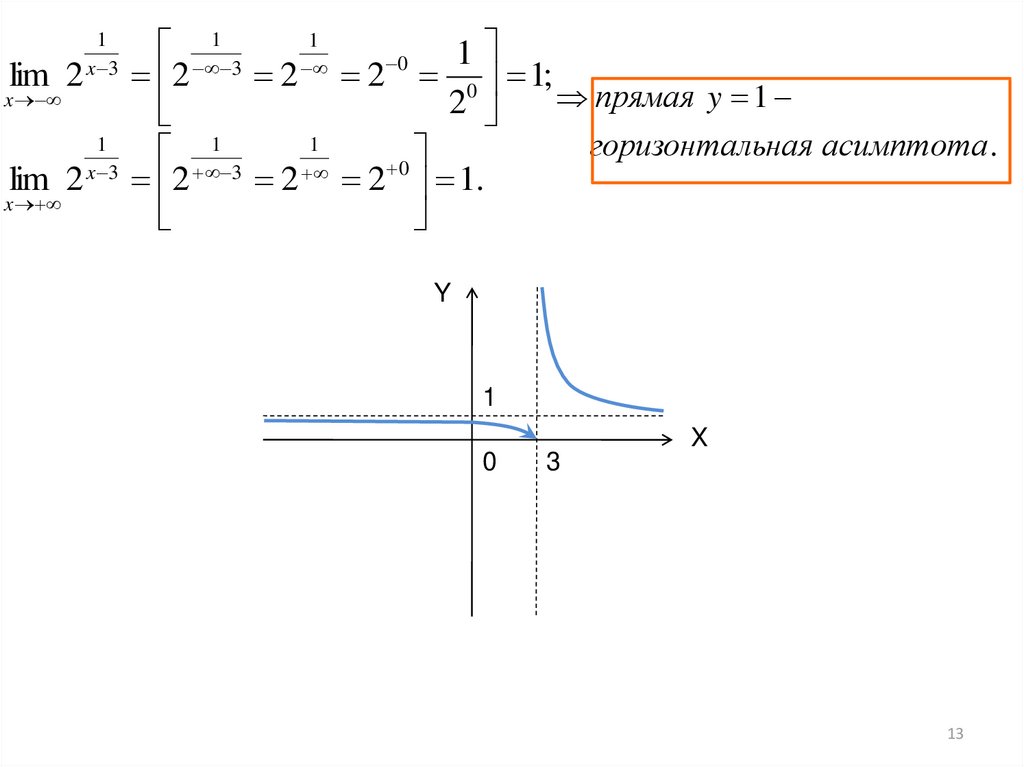
lim 21
x 3
x
lim 2
x
1
x 3
1
1 3
1
0
2
2 2 0 1;
прямая y 1
2
1
горизонтальная асимптота .
1 3
0
2
2 2 1.
Y
1
X
0
3
13
14.
x2 13) y
x 1
D y : ;1 1; x 1 точка разрыва.
2
x 2 1 1 0 1 2
lim
;
x 1 0 x 1
1 0 1 0
2
x 2 1 1 0 1 2
lim
;
x 1 0 x 1
1 0 1 0
x 1 точка разрыва второго рода,
прямая x 1 вертикальная асимптота .
14
15.
x2 12
2
2
x 2 1 1
1
x
x
lim
lim
;
x x 1
x x 1 0
1
2
2
2
x
x
x 1
lim
; горизонтальных асимптот нет.
x x 1
Исследуем наличие наклонной асимптоты, найдем пределы :
f x
lim
k
x
x
f x
x2 1
lim
lim
1 k 1.
x
x x 1 x
x
lim f x k x b
x
x2 1
x2 1 x2 x
lim
1 x lim
1 b 1.
x x 1
x
x 1
15
16.
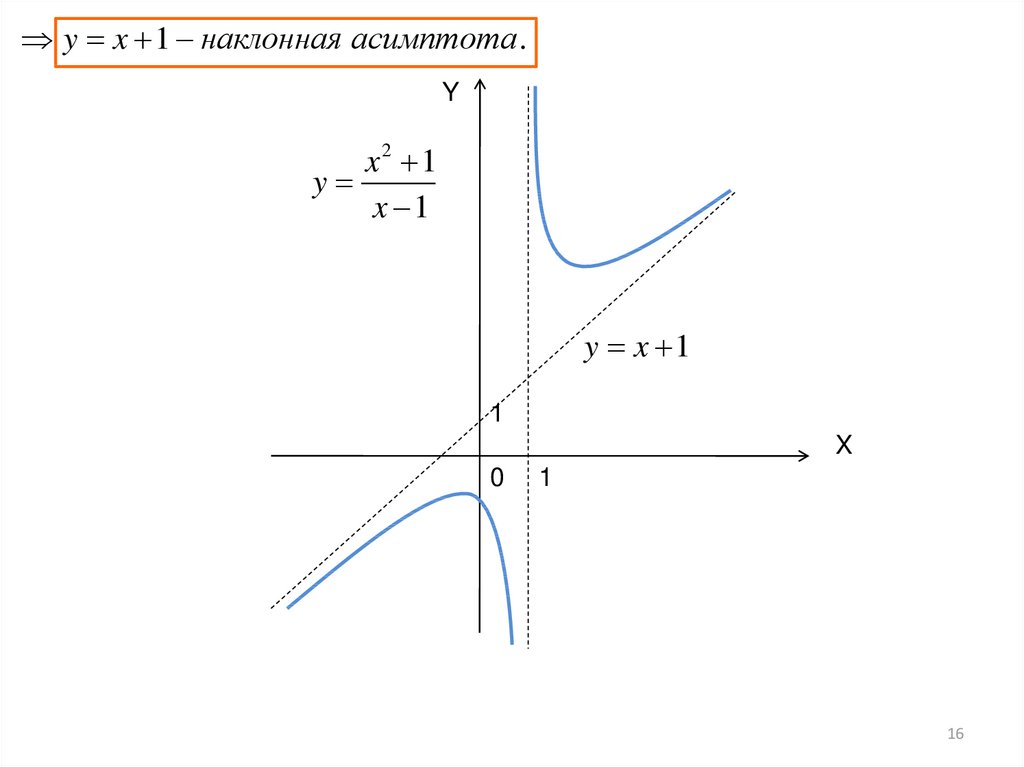
y x 1 наклонная асимптота .Y
x2 1
y
x 1
y x 1
1
X
0
1
16
17.
4 , x 0;4) y 4 x 2 , 0 x 2;
2 x, x 2.
0
x 0 0
2 x
2
x 0, x 2 точки возможного разрыва.
x 0
lim f ( x) lim 4 4;
x 0 0
4 x2
4
x 0 не является точкой разрыва.
lim f ( x) lim 4 x 2 4.
x 0 0
x 0 0
x 2
lim f ( x) lim 4 x 2 0;
x 2 0
x 2 0
x 2 0
x 2 0
lim f ( x) lim 2 x 4.
x 2 точкa разрыва I го рода.
17
18.
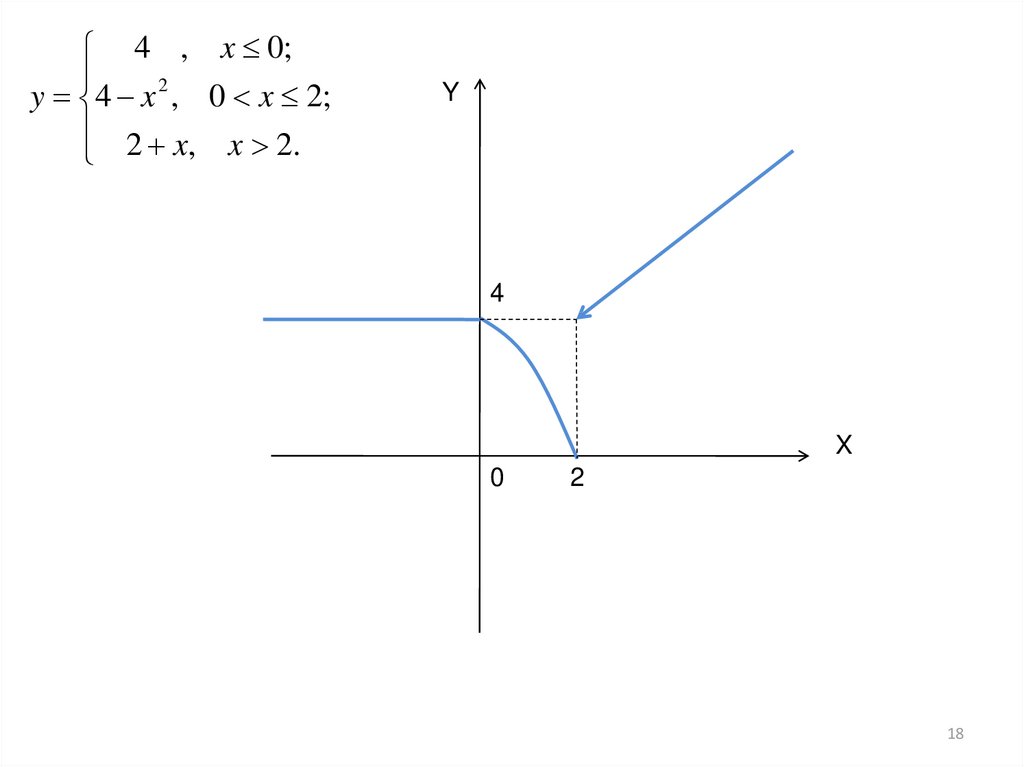
4 , x 0;y 4 x 2 , 0 x 2;
2 x , x 2.
Y
4
X
0
2
18














 mathematics
mathematics








