Преобразование графиков элементарных функций

1.

y=f(x)+a
y=f(x-a)
y=|f(x)|
y=f(|x|)
y=-f(x)
y=f(-x)
y=k·f(x)
y=f(k·x)

2.

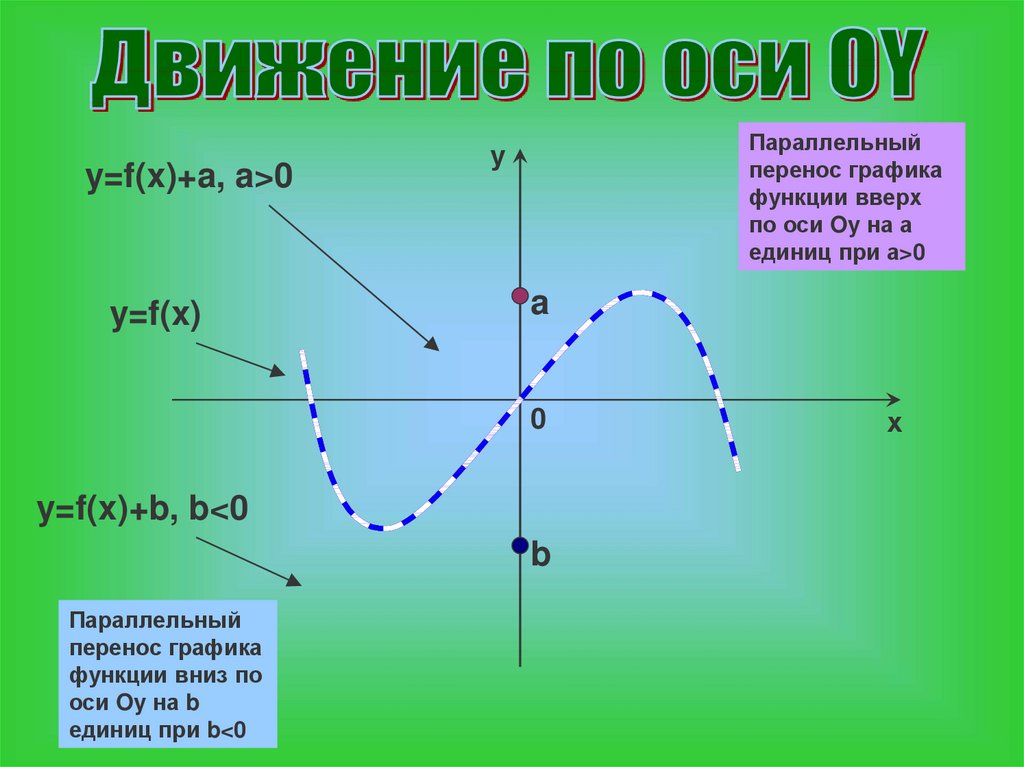
y=f(x)+a, a>0
y=f(x)
Параллельный
перенос графика
функции вверх
по оси Oy на а
единиц при а>0
у
a
0
y=f(x)+b, b<0
b
Параллельный
перенос графика
функции вниз по
оси Oy на b
единиц при b<0
х

3.

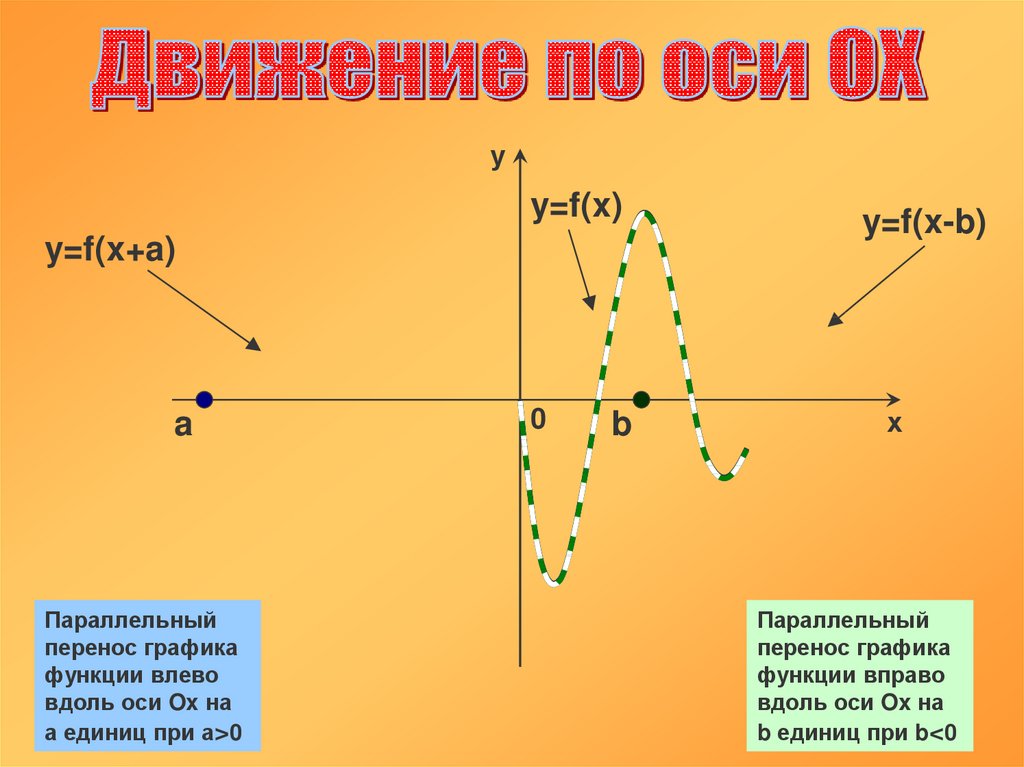
у
y=f(x)
y=f(x+a)
a
Параллельный
перенос графика
функции влево
вдоль оси Ox на
а единиц при а>0
0
b
y=f(x-b)
х
Параллельный
перенос графика
функции вправо
вдоль оси Ox на
b единиц при b<0

4.

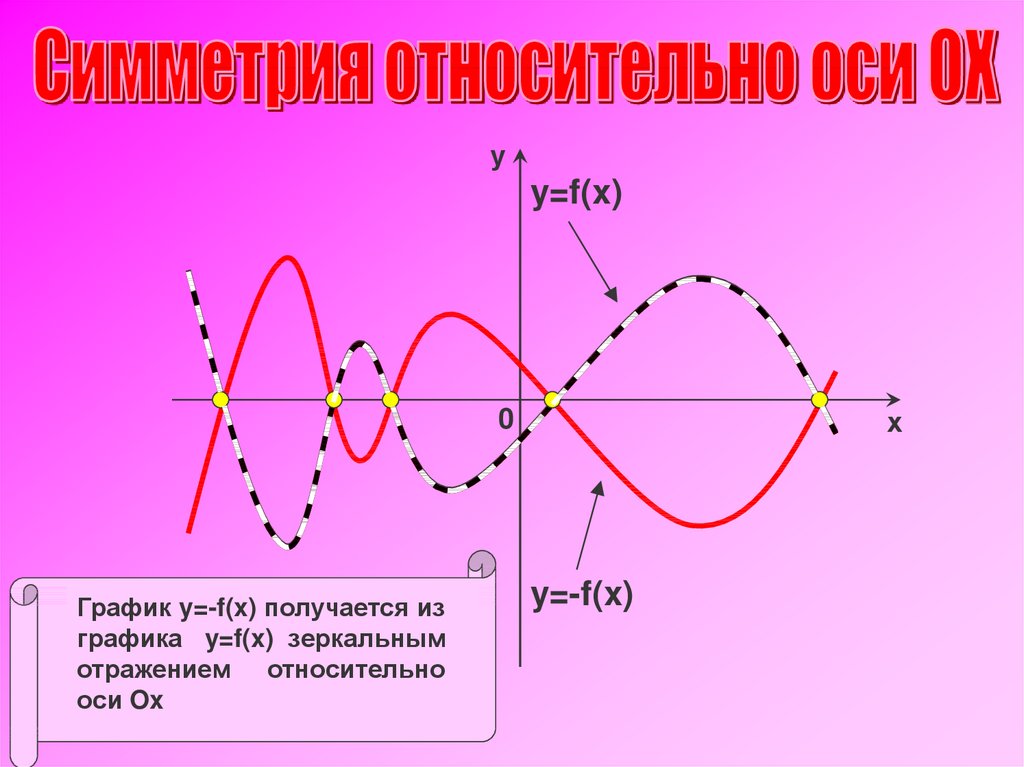
у
y=f(x)
х
0
График y=-f(x) получается из
графика y=f(x) зеркальным
отражением относительно
оси Ox
y=-f(x)

5.

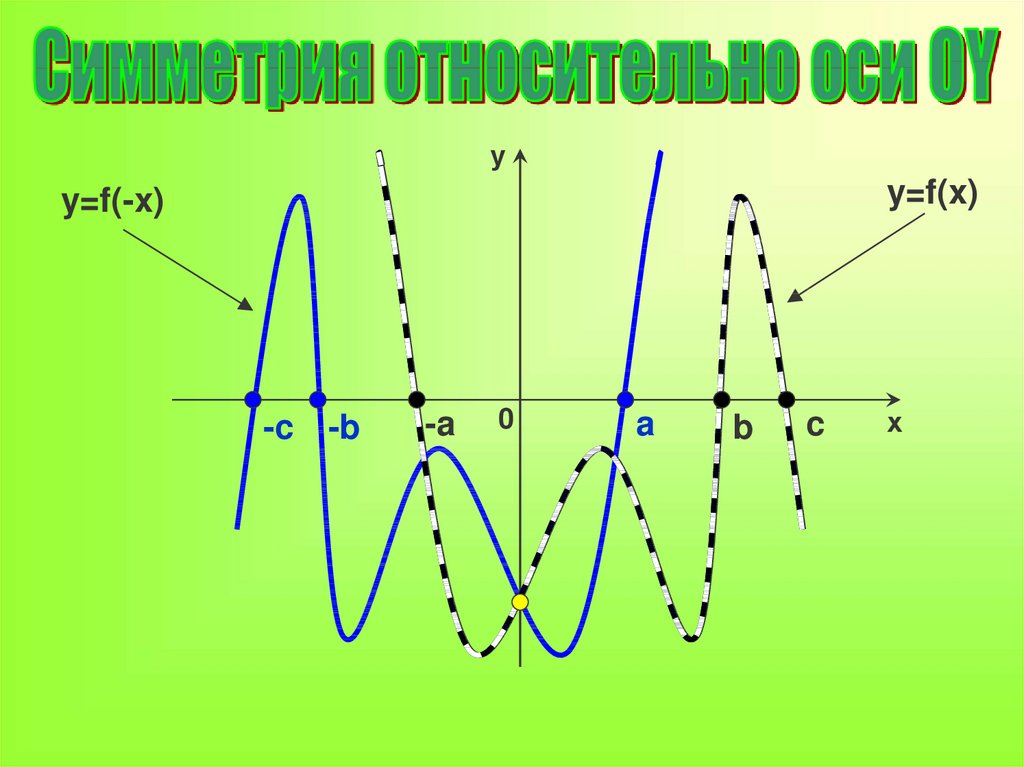
у
y=f(x)
y=f(-x)
-c -b
-a
0
a
b
c
х

6.

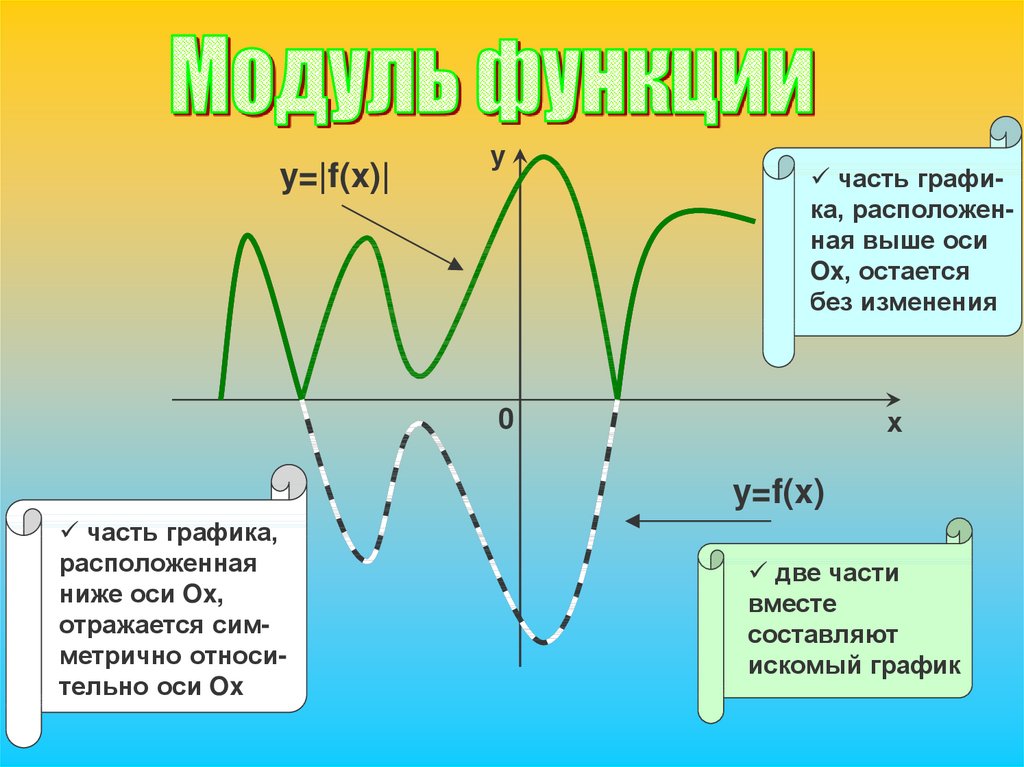
y=|f(x)|
у
часть графика, расположенная выше оси
Ox, остается
без изменения
х
0
y=f(x)
часть графика,
расположенная
ниже оси Ox,
отражается симметрично относительно оси Ox
две части
вместе
составляют
искомый график

7.

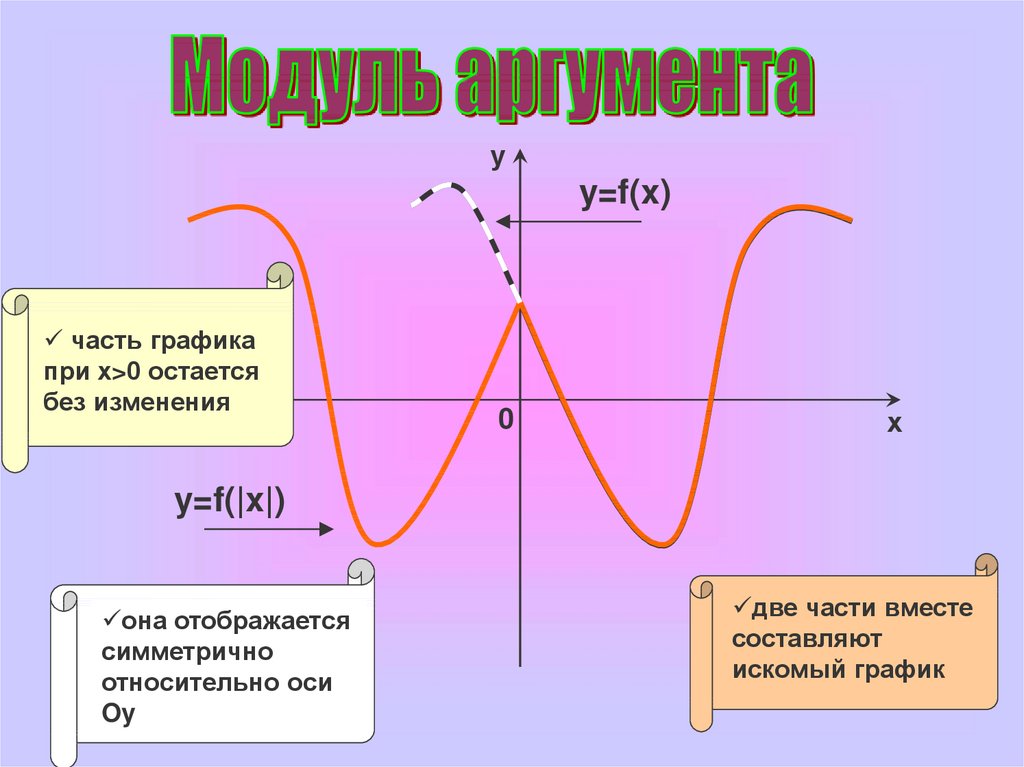
у
y=f(x)
часть графика
при х>0 остается
без изменения
0
х
y=f(|x|)
она отображается
симметрично
относительно оси
Oy
две части вместе
составляют
искомый график

8.

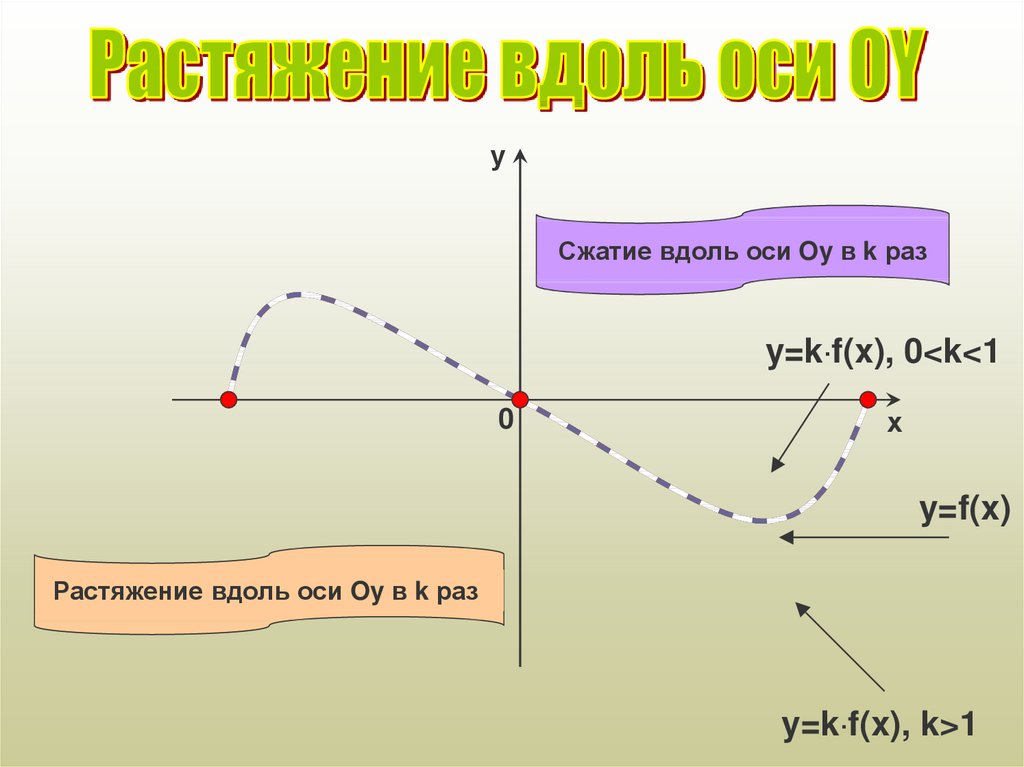
у
Сжатие вдоль оси Oy в k раз
y=k·f(x), 0<k<1
0
х
y=f(x)
Растяжение вдоль оси Oy в k раз
y=k·f(x), k>1

9.

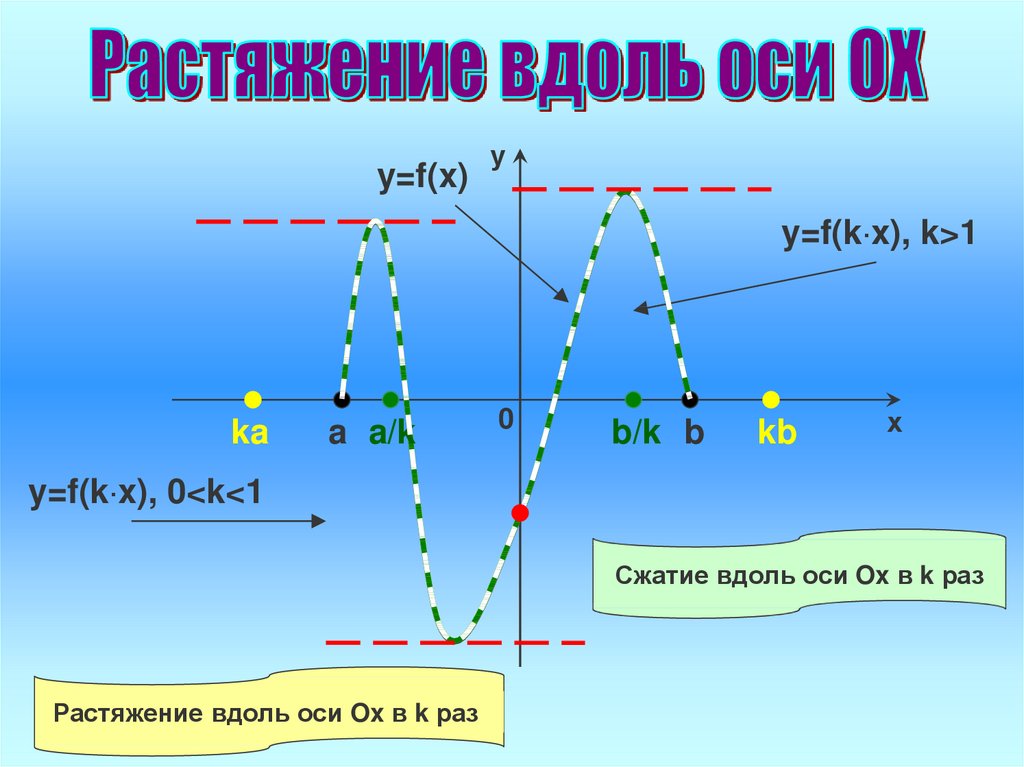
y=f(x)
у
y=f(k·x), k>1
ka
a a/k
0
b/k b
kb
х
y=f(k·x), 0<k<1
Сжатие вдоль оси Ox в k раз
Растяжение вдоль оси Ox в k раз

10.

Построить график функции:
3
f ( x ) 2 sin( 3x )
4

11.

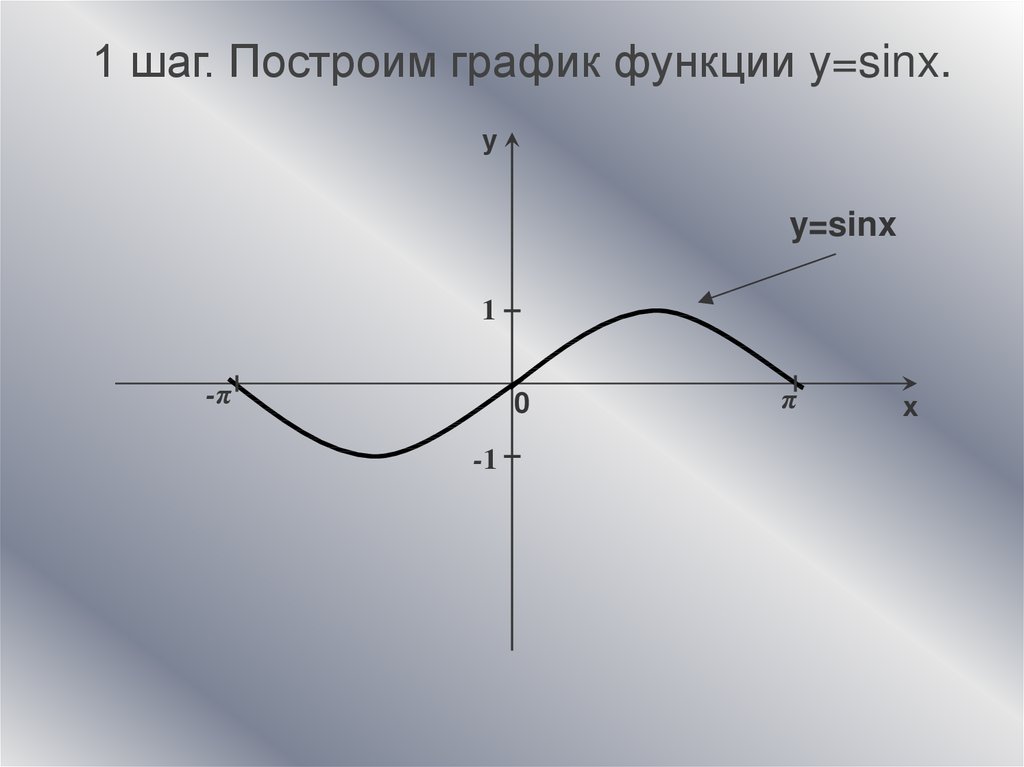
1 шаг. Построим график функции y=sinx.
у
y=sinx
1
-π
0
-1
π
х

12.

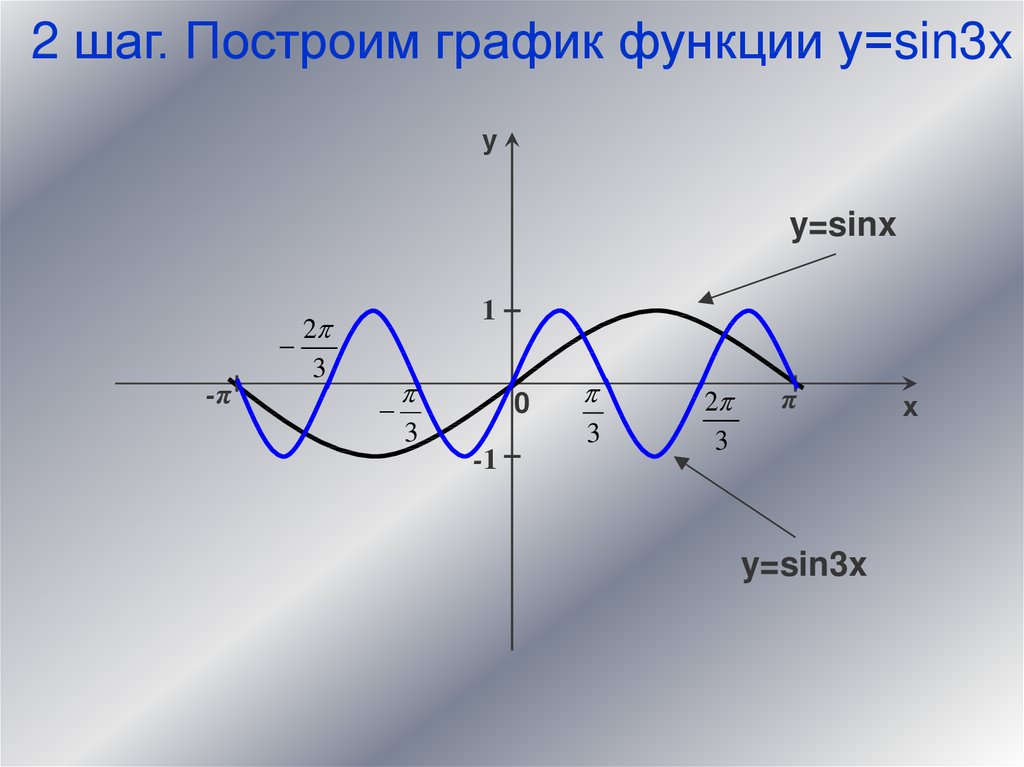
2 шаг. Построим график функции у=sin3x
у
y=sinx
1
2
3
-π
0
3
3
-1
2
3
π
y=sin3x
х

13.

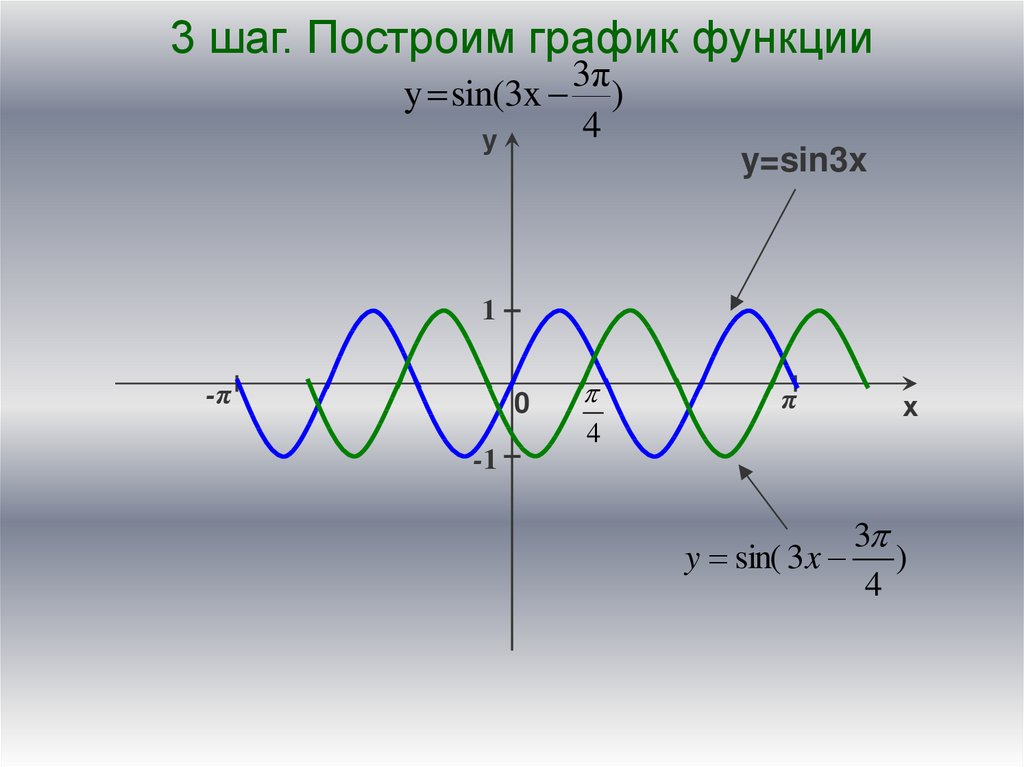
3 шаг. Построим график функции
y sin(3x
у
3π
)
4
y=sin3x
1
-π
0
π
х
4
-1
3
y sin( 3x )
4

14.

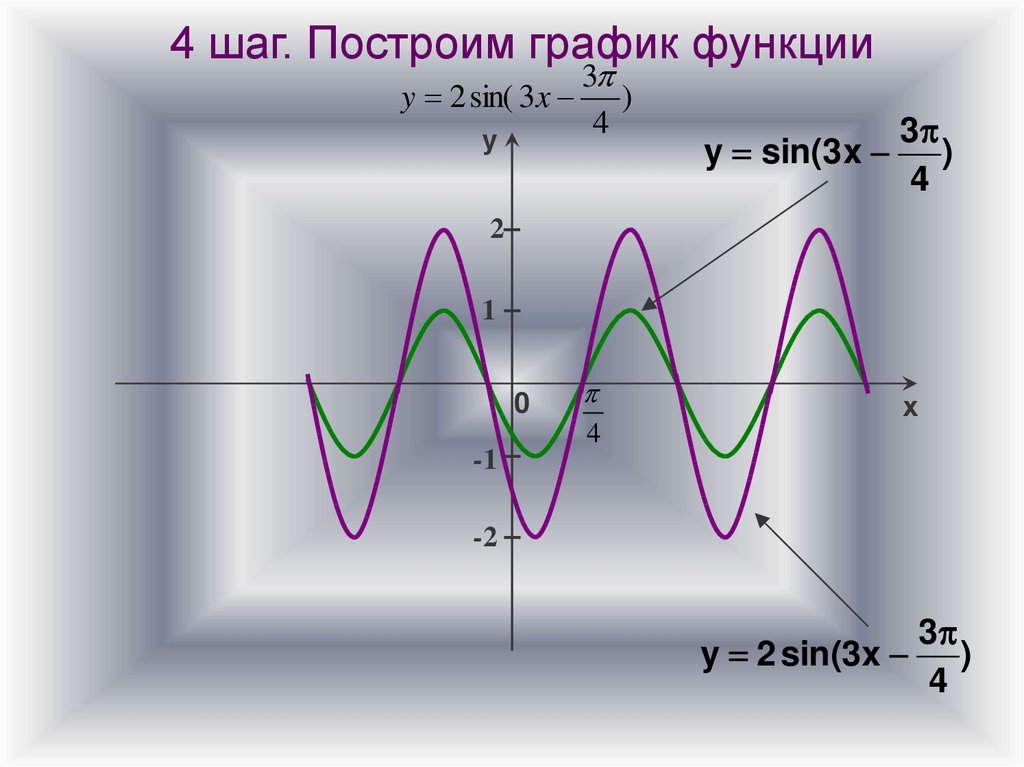
4 шаг. Построим график функции
3
y 2 sin( 3 x )
4
у
y sin(3x
3
)
4
2
1
0
х
4
-1
-2
y 2 sin(3x
3
)
4