Similar presentations:
Приложения производной. (Тема 4)
1. Приложения производной
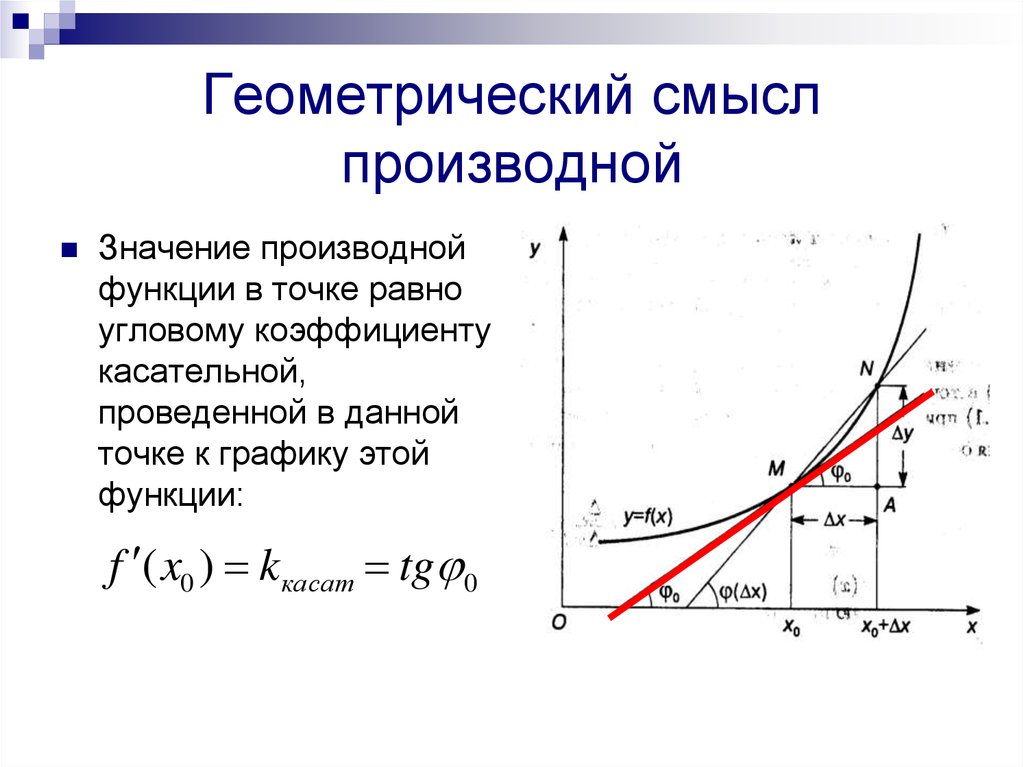
2. Геометрический смысл производной
Значение производнойфункции в точке равно
угловому коэффициенту
касательной,
проведенной в данной
точке к графику этой
функции:
f ( x0 ) kкасат tg 0
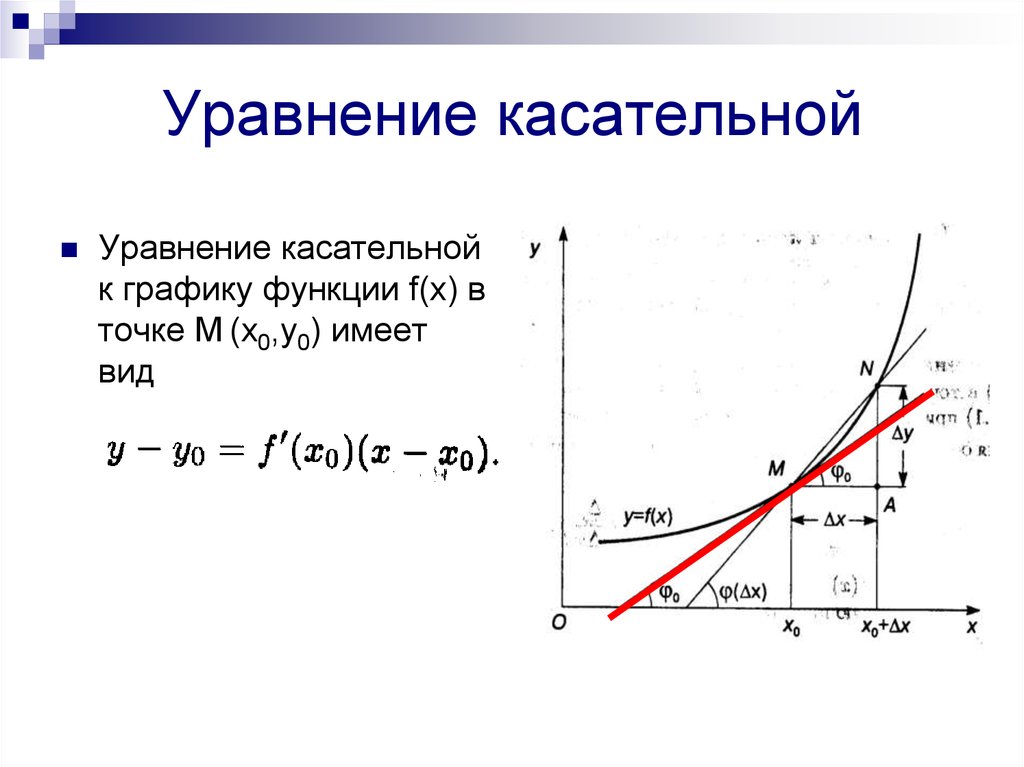
3. Уравнение касательной
Уравнение касательнойк графику функции f(x) в
точке М (х0,у0) имеет
вид
4. Дифференциал функции
Дифференциалом функции у = f(x) в точке х0называется линейная часть приращения
дифференцируемой функции в этой точке.
Обозначение: dy
Cимволически:
dy = f´(x)·Δх
или
dy = f´(x)·dх
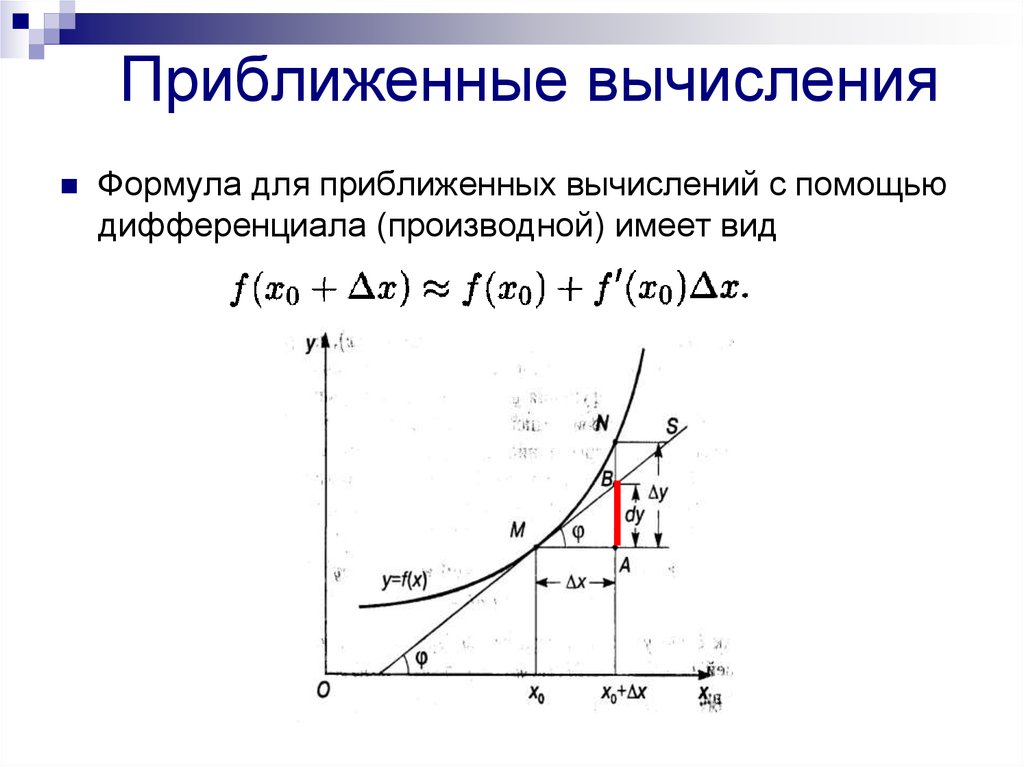
5. Приближенные вычисления
Формула для приближенных вычислений с помощьюдифференциала (производной) имеет вид
6. Правило Лопиталя
Пусть функции f(x) и g(х) определены идифференцируемы в некоторой окрестности точки а за
исключением, быть может, самой точки a. Кроме того,
пусть lim f ( x) lim g ( x) 0, причем g'(х) ≠ 0 в указанной
x a
x a
окрестности точки а. Тогда если существует предел
f ' ( x) (конечный или бесконечный)
отношения
lim
x a
g ' ( x)
f ( x)
то существует и предел ,lim
x a g ( x )
причем справедлива формула
Правило Лопиталя можно применять неоднократно
7. Ряд Тейлора
Функцию f(x), имеющую (n+1) производных в точкех = х0, можно разложить в степенной ряд по формуле
Тейлора
8. Ряд Маклорена
Функцию f(x), имеющую (n+1) производных в точкех = 0, можно представить по формуле Маклорена:
9. Разложения функций
Разложения трансцендентных функций по формулеМаклорена:
10. Схема исследования функции
1.2.
3.
4.
5.
6.
7.
Область определения
Четность-нечетность
Пересечение с осями координат
Непрерывность, асимптоты графика
Промежутки монотонности и
экстремумы (с помощью у )
Промежутки выпуклости графика и
точки перегиба (с помощью у )
График по результатам исследования
11. Асимптоты графика
Вертикальные (х = а): среди точекразрыва второго рода из условия
lim f ( x)
x a
Наклонные (у = кx + b)
и горизонтальные (у = b):
f ( x)
lim
k
x
x








 mathematics
mathematics








