Similar presentations:
Разветвленная RLC – цепь Резонанс токов
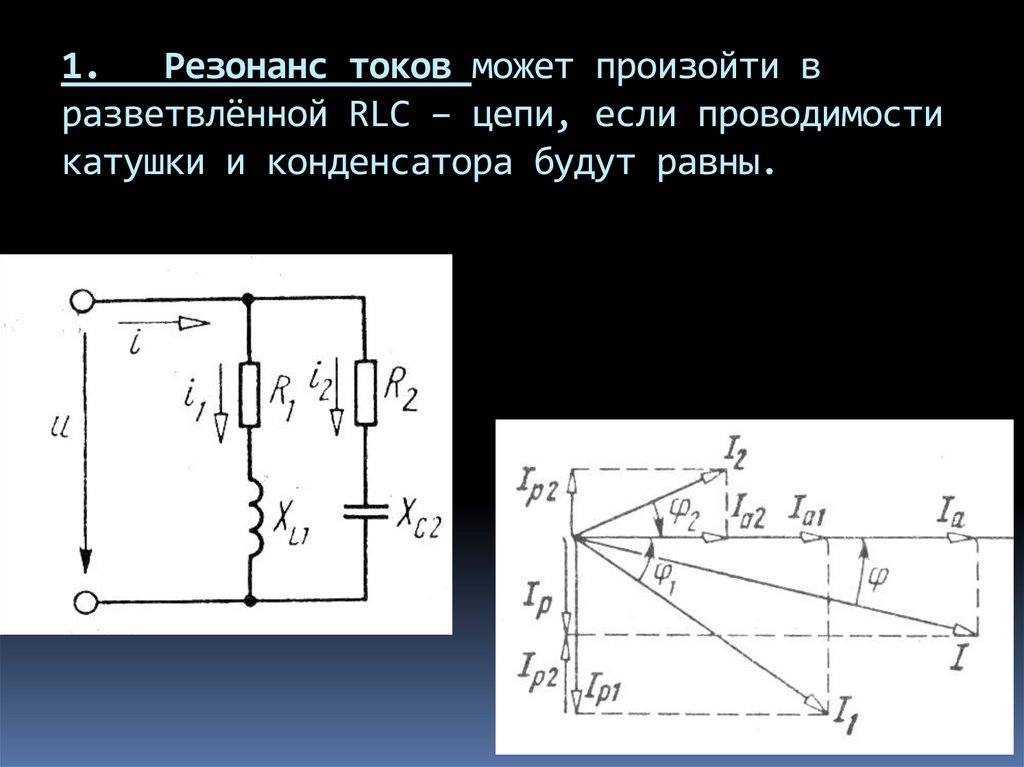
1. Разветвленная RLC – цепь Резонанс токов
РАЗВЕТВЛЕННАЯ RLC – ЦЕПЬРЕЗОНАНС ТОКОВ
1. Расчет методом проводимостей
2. Явление резонанса токов.
2. 1. Резонанс токов может произойти в разветвлённой RLC – цепи, если проводимости катушки и конденсатора будут равны.
3. Разветвленную цепь рассчитывают методом проводимостей, раскладывая токи на активные и реактивные составляющие:
Активные составляющие токов:U R1
I A1 I1 cos U g1
z1 z1
I A2
U R2
I 2 cos
U g2
z2 z2
Реактивные составляющие токов:
U X1
I Р1 I1 sin 1
U b1
z1 z1
I Р2
U X2
I 2 sin 2
U b2
z2 z2
g активная проводимость(См) b реактивная проводимость(См)
Ток неразветвленной части цепи:
I ( I A1 I A 2 ) 2 ( I P1 I P 2 ) 2 U Y
ïîëíàÿ
ïðîâîäèìîñ
òü :
Y ( g1 g 2 ) 2 (b1 b2 ) 2
4. 2. Резонанс токов –это явление в цепи с параллельным колебательным контуром, когда ток в неразветвленной части цепи совпадает
по фазе с напряжением источника.Признаки резонанса токов:
Полная проводимость минимальна и чисто
активна Y=g
Ток неразветвленной части цепи минимален и
совпадает по фазе с напряжением источника
I=U· g =>min
Ток катушки равен току конденсатора и оба во
много раз превышают ток источника.
IL=Ic>>I
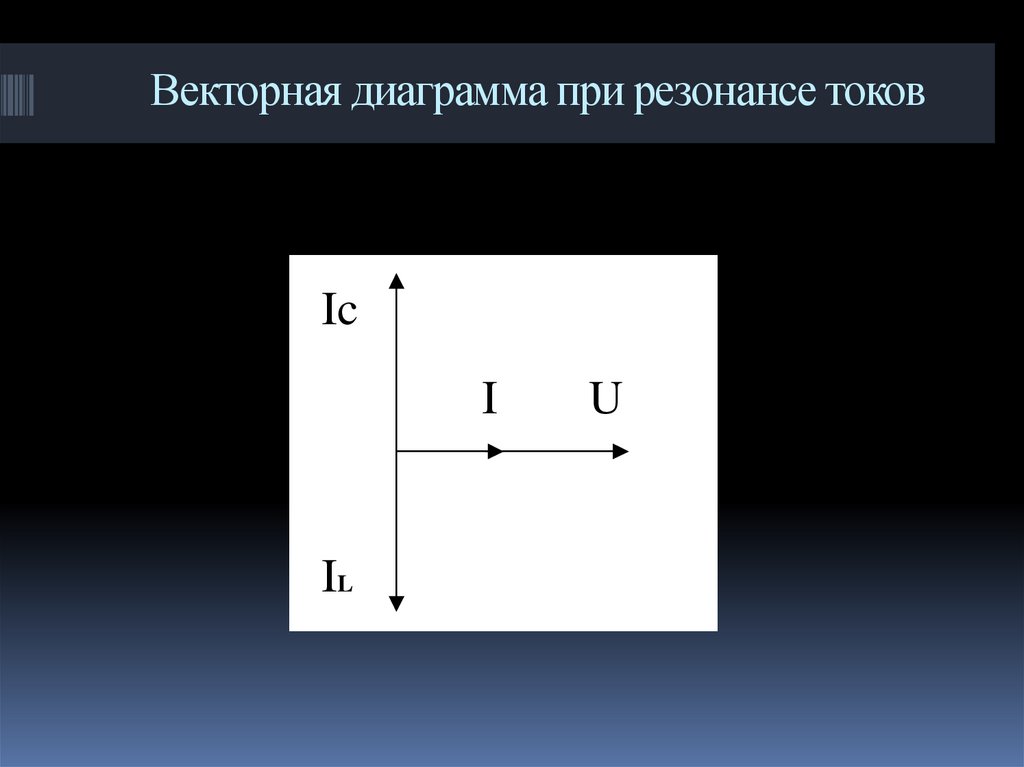
5. Векторная диаграмма при резонансе токов
IcI
IL
U



 electronics
electronics








