Similar presentations:
Экономический факторный анализ
1. Тема 5. Экономический факторный анализ
2. Тема 5. Экономический факторный анализ
• 1. Понятие экономическогофакторного анализа: его виды
• 2. Типы факторных систем и их
преобразования
• 3. Методы количественной
оценки влияния факторов на
результат
• 4. Стохастическое
моделирование
3. Тема 5. Экономический факторный анализ
Фактор – это показатель, от которого зависит другойпоказатель – результативный.
Факторная система – совокупность фактора и
результата, связанная причинно-следственной
связью.
Модель факторной системы (факторная модель) – это
формула, выражающая взаимосвязь между
результатом и фактором.
• Экономический факторный анализ – это раскрытие
набора прямых факторов, влияющих на
результат, и измерение влияния этих факторов на
величину результата.
• Качественный факторный анализ – это
определение факторов и взаимосвязи с
результатом. Качественный анализ заканчивается
построением факторной модели.
• Количественный факторный анализ – это оценка
влияния каждого фактора на изменение
результата.
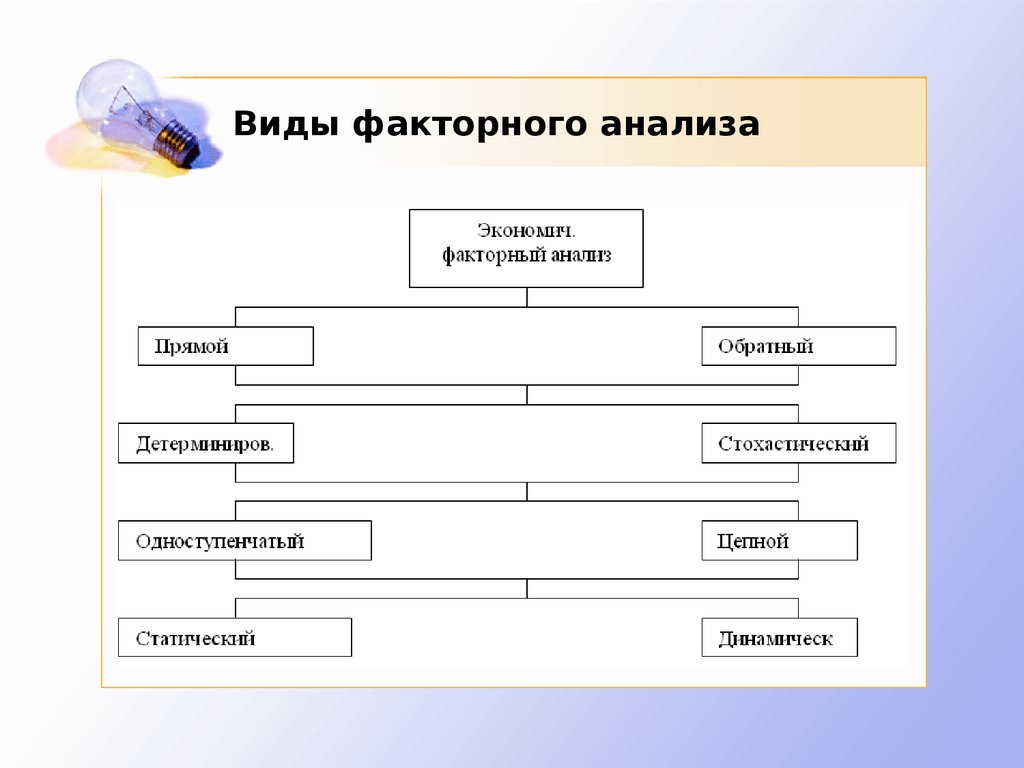
4. Виды факторного анализа
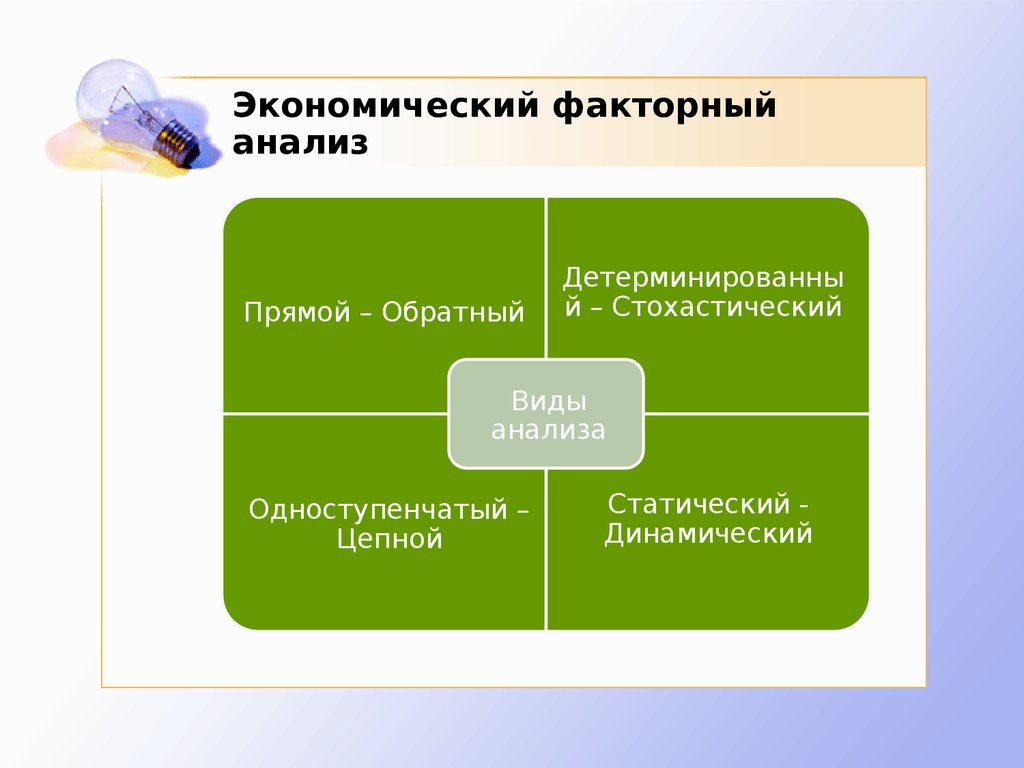
5. Экономический факторный анализ
Прямой – ОбратныйДетерминированны
й – Стохастический
Виды
анализа
Одноступенчатый –
Цепной
Статический Динамический
6. Виды факторного анализа
Прямой анализ – оценка влияния каждого
фактора.
Обратный анализ (синтез) – оценка влияния
комплекса факторов.
Детерминированный факторный анализ
применяется при функциональной связи
результата и фактора. Функциональная связь –
связь, когда определенному значению фактора
соответствует одно определенное значение
результата.
Стохастический факторный анализ
применяется, если связь результата и факторов
вероятностная ( т.е. определенному значению
факторов соответствует целая совокупность
значений результата).
Одноступенчатый анализ – анализ влияния
факторов первого уровня.
Цепной анализ – анализ влияния факторов
более низкого уровня.
7. Виды факторного анализа
Статический анализ– этоисследование зависимости
результата от факторов без
учета влияния времени.
• Динамический анализ исследование зависимости
результата от факторов с
учетом влияния времени.
8. Детерминированный факторный анализ
• ДФА представляет собойметодику исследования
влияния факторов, которые
имееют с результативным
показателем функциональную
связь (результат есть функция
от этих факторов).
9. Типы детерминированных факторных систем
n1. Аддитивные модели
y Xi
i 1
2. Мультипликативные
модели
3. Кратные модели
4. Смешанные модели
n
y П xi x1 x2 ... xn
i 1
x1
y
x2
y x1 x2 x3
10. Требования, которые необходимо выполнять при моделировании детерминированных факторных систем
• 1. Факторы, включаемые в модель, должныреально существовать, а не быть
абстрактными величинами или явлениями.
• 2. Факторы должны быть не только
элементами формулы, но и находится в
причинно-следственной связи с изучаемым
явлением.
• 3.Все факторы дожны быть количественно
измеримы.
• 4.Факторная модель должна обеспечивать
возможность измерения влияния отдельных
факторов (сумма изменений
результативного показателя за счет
отдельных факторов должна равняться
общему изменению результативного
11. Преобразование детерминированных факторных систем
• Преобразование факторных системотносится только к кратным
моделям.
• Почему только кратные модели?
• Чтобы в качестве факторов
выступали показатели не в виде
абсолютных величин, а в виде
относительных величин.
• Относительные величины
обеспечивают сравнимость данных.
12. Методы преобразования факторных систем
• 1. Метод удлинения факторныхсистем
• 2. Метод расширения
факторных систем
• 3. Метод сокращения
факторных систем
13.
• В результате пребразованияполучается модель с новым
набором факторов, имеющих
экономический смысл,
экономическую
интерпретацию.
14. Метод удлинения факторных систем
a a1 a2 a1 a2у
b
b
b b
15. Метод удлинения факторных систем. Пример
ЗМЗ ЗПСВ АМ ПР
Зна1ТП
ТП
ТП
МЗ ЗПСВ АМ ПР
ТП
ТП
ТП ТП
МЕ ЗПЕ АМЕ ДПР
16. Метод расширения факторных систем
a a k m ny
b b k m n
a k m n
k m n b
17. Метод расширения факторных систем. Пример
ВП ОС ВП ОСПТ
Ч
ОС ОС Ч
ФО ФВ
18. Метод сокращения факторных систем
aa a/с c
y
b b/с b
c
19. Метод сокращения факторных систем. Пример
ВП BП / Ч ПТФО
OC ОС / Ч ФВ
20. Методы количественной оценки влияния факторов на результат
Siс! В учебниках написано: « Метод индексов
применяется для двухфакторных
мультипликативных моделей с одним
количественным и одним качественным
признаком». - It is wrong.
Метод индексов применяют и для анализа
средних величин, где оба фактора
качественные, относительные, и для
трехфакторных моделей, например, модель
финансового результата.
Метод цепных подстановок. Факторы
последовательно заменяются с базисного
уровня на отчетный. Разности двух соседних
значений характеризуют влияние каждого
фактора
Метод взвешенных конечных разностей.
Величина влияния каждого фактора
определяется по всем возможным вариантам
подстановки и находится среднее значение.
21. Метод индексов
nB Qi Pi ,
i 1
n
B
Q
i1
Pi1
Q
i0
Pi 0
i 1
n
i 1
B Q P
n
Q
Q
i1
Pi 0
Q
i0
Pi 0
i 1
n
i 1
n
P
Q
i1
Pi1
Q
i1
Pi 0
i 1
n
i 1
22. Метод индексов для средних величин
nЗ
Ч
i 1
i
n
Ч
i 1
n
З
Ч
i 1
i1
Ч
:
i1
i
n
Зi1
n
i 1
Зi
Ч
i 1
i0
Зi 0
n
Ч
i 1
i0
23. Индексный метод
• «+» метода: простота и точноеразложение (без остатков).
• «-» метода: результат факторного
разложения зависит от очередности
факторов.
24. Метод индексов
• Метод индексов имеет 2 задачи, 2стороны:
• 1.Аналитическую- с помощью метода
индексов
общее
изменение
результативного
показателя
разлагается на изменения за счет
отдельных факторов.
• 2. Синтетическую – с помощью
метода
индексов
обобщается
изменение
по
совокупности
непосредственно не поддающихся
обобщению элементов.
25. Метод индексов
• Метод индексов, т. о. сочетает в себеанализ и синтез:
• анализ относится к признакам,
• синтез относится к элементам
совокупности!
• Анализируя, разлагая, одно, мы в
тоже время синтезируем другое!
• В этом –сущность, главное
достоинство метода индексов!
26. Метод цепных подстановок
• Суть метода цепных подстановокзаключается в последовательной
замене значений факторов с
базисного уровня на отчетный.
Разности двух соседних значений
результативного показателя
характеризуют влияние каждого
фактора .
• Число вспомогательных значений
результативного показателя на
единицу меньше числа факторов.
27. Метод цепных подстановок
y f (a, b, c, d )yo f (ao , bo , co , d o ) базисное значение
ya f ( a1 , b0 , c0 , d 0 ) промежуточ ное значение 1
ya y0 ya
28. Метод цепных подстановок
yb f (a1 , b1 , c0 , d 0 ) промежуточ ное значение 2yb ya yb
yc f (a1 , b1 , c1 , d 0 ) промежуточ ное значение 3
yc yb yc
y1 f (a1 , b1 , c1 , d1 ) фактическо е отчетное значение
y1 yc yd
29. Метод цепных подстановок
y1 y0 ya yb yc yd30. Метод цепных подстановок
Плюсы метода:
1. Простота расчетов
2. Точное разложение
3. Метод универсальный
Минусы метода: разложение зависит от
последовательности (очередности)
замены факторов :
а) определение правильной экономически
обоснованной последовательности
факторов (сначала количественные
факторы, затем – качественные).
б) поиск метода, не зависящего от
последовательности факторов.
31. Алгоритм проведения факторного анализа методом цепных подстановок
• 1. Составить детерминированнуюфакторную модель
результативного показателя.
• Правильность составленной
модели проверяем через единицы
измерения.
• Кратные модели необходимо
преобразовывать.
32. Алгоритм проведения факторного анализа методом цепных подстановок
• 2. Классификация факторов на:количественные и
качественные; первичные и
вторичные; абсолютные и
относительные; изменяющиеся
в процессе первыми и
изменяющиеся в процессе
вторыми,- для того, чтобы
определить очередность
изучения влияния факторов на
изменение результативного
показателя.
33. Алгоритм проведения факторного анализа методом цепных подстановок
• 3. Рассчитать изменениерезультативного показателя за
счет изменения первичного
фактора.
• Правило 1.При измерении
влияния первичного фактора
вторичный фактор (фактор,до
которого еще не дошла
очередь) фиксируется на
уровне базисного периода.
34. Алгоритм проведения факторного анализа методом цепных подстановок
• 4. Рассчитать изменениерезультативного показателя за
счет изменения вторичного
фактора.
• Правило 2. При изучении влияния
вторичного (третичного и т.д.)
фактора первичный фактор( или
фактор, влияние которого
изучалось ранее,) фиксируется на
уровне отчетного (текущего)
периода.
35. Алгоритм проведения факторного анализа методом цепных подстановок
• 5. Провести проверку:• общее изменение
результативного показателя
равно алгебраической сумме
изменений результативного
показателя за счет изменений
факторов.
36. Прием абсолютных разностей
• Используют длямультипликативных и
мультипликативно-аддитивных
моделей.
• Простота расчетов.
• Для мультипликативных
моделей применяют правило
«махания рук».
37. Прием абсолютных разниц
y a b c dya (a1 a0 ) b0 c0 d 0
yb a1 (b1 b0 ) c0 d 0
yc a1 b1 (c1 c0 ) d 0
yd a1 b1 c1 (d1 d 0 )
38. Прием абсолютных разностей
• Правило «махания рук» :• фактор, стоящий справа от
фактора, влияние которого
изучается, фиксируется на
базисном уровне , а фактор,
стоящий слева от фактора,
влияние которого изучается,
фиксируется на отчетном уровне.
39. Метод взвешенных конечных разностей
40. Метод взвешенных конечных разностей
«+» метода:
1. Не зависит от
последовательности факторов
2. Точное разложение
3. Универсальный метод.
«-» метода:
1. Трудоемкий метод.
41. Интегральный метод факторного анализа
«+» метода:• более точный по сравнению с цепными
подстановками (поскольку
дополнительный прирост результативного
показателя от взаимодействия факторов
присоединяется не к последнему фактору,
а делится поровну между ними);
• результат не зависит от порядка
расположения факторов;
• универсальный.
42. Формулы для расчета интегральным методом
f x yf ( X )
f (Y )
1
x y0 x y
2
1
y x0 x y
2
43. Формулы для расчета интегральным методом
f xyz1
1
f x x( y 0 z1 y1 z0 ) x y z
2
3
1
1
f y y ( x0 z1 x1 z 0 ) x y z
2
3
1
1
f z z ( x 0 y1 x1 y0 ) x y z
2
3
44. Кратная модель
xf
y
f ( X )
x
y1
ln
y
y0
f (Y ) f общ fx
45. Модель кратно-аддитивная
xf
y z
f ( X )
f общ f1 f 0
y1 z1
x
n
y z
y0 z0
f (Y )
f ( Z )
f общ f ( X )
y z
f общ f ( X )
y z
y
z
46. Логарифмический метод
Используется только вмультипликативных и кратных
моделях.
«+» метода:
• результат не зависит от порядка
(месторасположения) факторов, как и
в интегральном.
• по сравнению с интегральным – более
точный (с помощью
логарифмирования результат
совместного влияния факторов
распределяется пропорционально
доли изолированного влияния
каждого фактора на уровень
результативного показателя
47. Логарифмический метод
f ( X )x1
g
x0
f общ .
f1
g
f0
f ( y )
y1
g
y0
f общ .
f1
g
f0
f x y
48. Стохастическое моделирование
• Применяется, если связь результатаи факторов вероятностная ( т.е.
определенному значению факторов
соответствует целая совокупность
значений результата).
• Факторы должны быть не только
элементами формулы, но и
находиться в причинно-следственной
связи с результатом (это требование
называется «познавательная
ценность модели»).
• Все факторы должны быть
количественно измерены и иметь
источники информации.
49.
• Признаки-факторы не должныдублировать друг друга, т.е. быть
коллинеарными.
• Признаки-факторы не должны быть
составными частями
результативного признака.
50. Стохастическое моделирование
yˆ a b1 x1 b2 x2 ... bk xk51. Применение результатов стохастического моделирования в анализе
• 1. Для оценки эффективностииспользования производственного
потенциала организации
уi уˆ i U i ,
если U i 0, то использова ние производст венного
потенциала выше, чем в среднем по совокупнос ти.
52.
• где У - рентабельность продаж,руб./руб.;
Х1-материалоотдача.руб./руб.;
• Х2 -фондоотдача, руб./руб.;
• Х3- производительность труда,
руб./чел.;
• Х4- продолжительность оборота
оборотных средств, дней;
• Х5 - удельный вес продукции высшей
категории качества.
53.
54.
55. Применение результатов стохастического моделирования в анализе
• 2. Для прогнозированияyˆ a b1 x1 b2 x2 ... bk xk ,
где x , x ,..., x
'
1
'
2
прогнозные
факторов .
'
k
значения
56. Применение результатов стохастического моделирования в анализе
• 3. Для выбора объектовнаилучших с точки зрения
вложения инвестиций
57. 3. Выбор объектов наилучших с точки зрения вложения инвестиций
( yi y ) ( yˆi y ) ( yi yˆi ),58. 3. Выбор объектов наилучших с точки зрения вложения инвестиций
• Отклонение, обусловленноеразмером производственного
потенциала
( yˆi y )
59. 3. Выбор объектов наилучших с точки зрения вложения инвестиций
• Отклонение, обусловленноеэффективностью
использования
производственного потенциала
( yi yˆi )
60. 3. Выбор объектов наилучших с точки зрения вложения инвестиций
• Объектом вложенияинвестиций является объект, у
которого
( yˆi yi ) 0, а
( yi yˆi ) 0
61. Применение результатов стохастического моделирования в анализе
• 4. Для расчета резервовy bk xk


















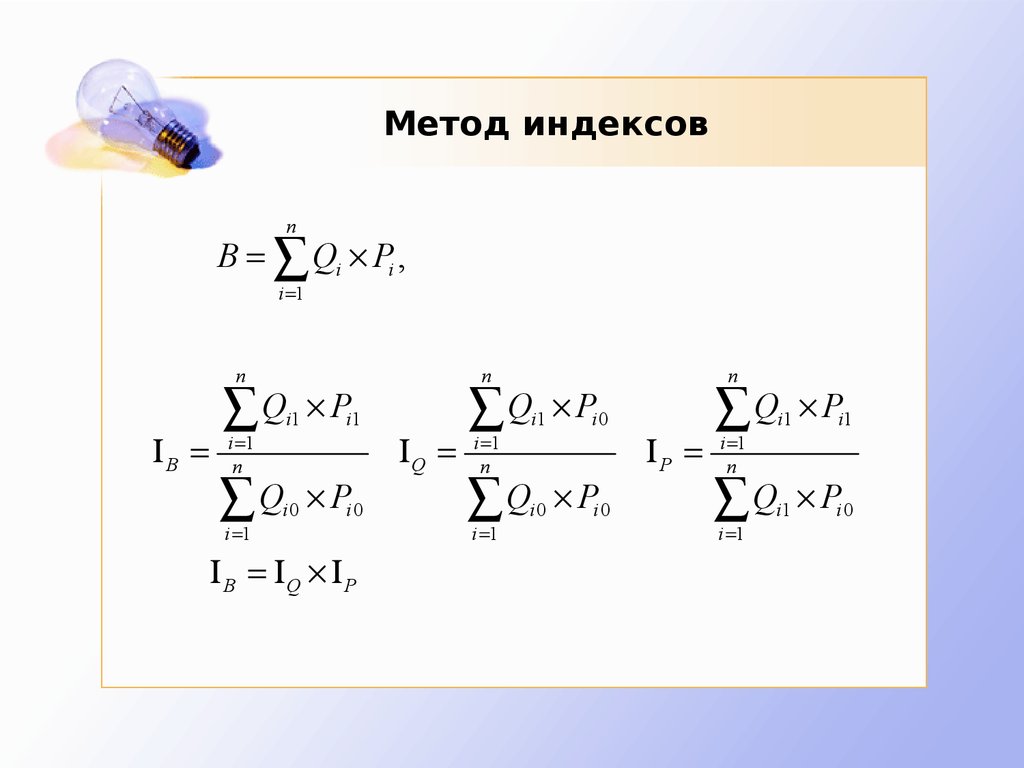







































 economics
economics








