Функции и графики в заданиях ОГЭ (Ракурс. Математический объект.)

1.

Муниципальное общеобразовательное учреждение «Средняя общеобразовательная школа № 4»
«Функции и графики в заданиях ОГЭ»
(Ракурс. Математический объект.)
Выполнили:
Бугрова Юлия, 9б класс
Растегаева Алина, 9б класс
Руководитель: Якушева Валентина Николаевна,
учитель математики первой квалификационной
категории
Ртищево, 2016

2.

Предмет: свойства функций, их применение для построения графиков
кусочных - заданных функций.
Объект: кусочно - заданные функции.
Гипотеза: если проследить закономерности в решении задач, то можно
составить алгоритм действий, что поможет и облегчит подготовку к ОГЭ
по математике, а также, увеличится интерес к рассматриваемой теме и
повысится качество усвоения пройденного материала
Цель: получить более широкие знания о функции, о графиках функций и о
преобразованиях графиков функций, изучить виды кусочно - заданных
функций и научиться строить их графики.
Задачи:
собрать и обработать информацию,
систематизировать задачи открытого банка заданий по данной теме,
представить решение задач по данной теме,
оформить презентацию.
Методы исследования: наблюдение, анализ, обобщение, сравнение.

3. Термин функции

Термин "функция" (от латинского
function – исполнение, совершение)
впервые ввел немецкий математик
Готфрид Лейбниц(1646-1716).

4. Понятие функции

Функцией называется зависимость переменной y от
переменной x, причем каждому значению x соответствует
единственное значение y.
Значение y, соответствующее заданному значению x, называют
значением функции.
Переменную x называют независимой переменной или
аргументом, а переменную y – зависимой переменной, так как
значение функции (y) зависит от значения аргумента.
y=f(x)

5. Пример:

Путь имеется множество Х (яблоко, самолет, груша, стул) и
множество У (человек, паровоз, квадрат). Зададим функцию f
следующим образом: y=f : (яблоко, человек), (самолет, паровоз),
(груша, квадрат), (стул, человек). Если ввести переменную x,
пробегающую множество Х и переменную y, пробегающую
множество У, указанную функцию можно задать аналитически, т.е.
с помощью формулы y=f(x).

6. Способы задания функций

Аналитический ( с помощью формул)
Пример: y=2x+5
Табличный
Примером может служить таблица квадратов
График
Словесное задание функции

7. Графики функции

y
Y=X2
y = k /x
k>0
O
y
B(0; b)
b
a
A(-b/k; 0)
О
y = kx +b
k>0
x
x

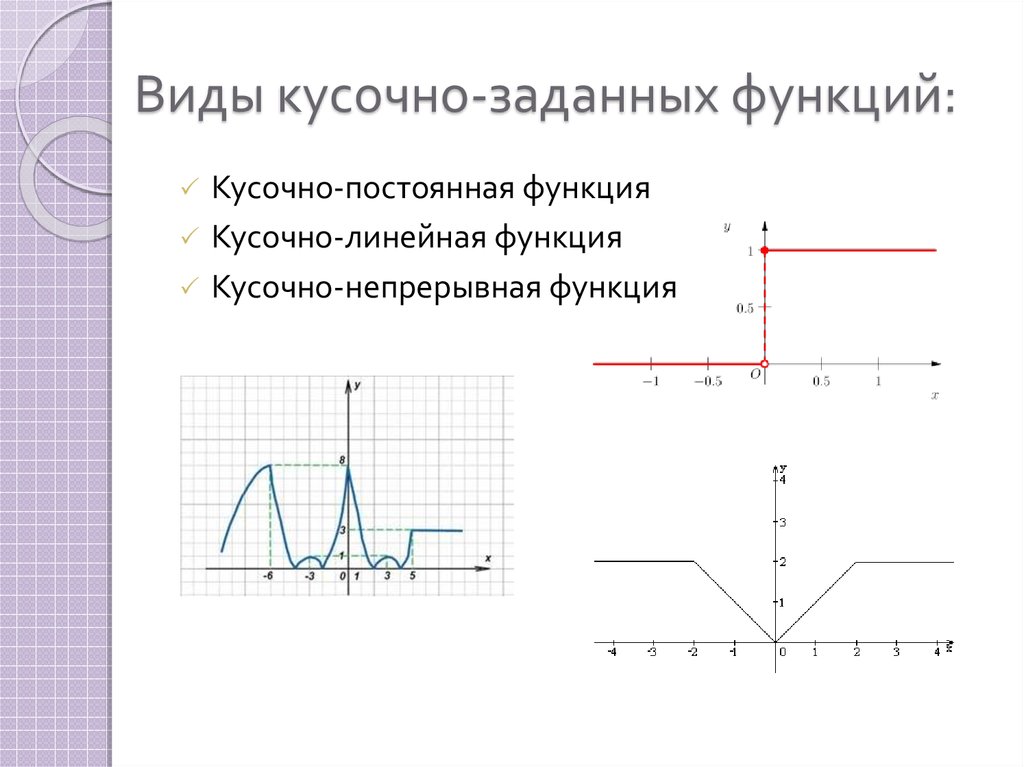
8. Виды кусочно-заданных функций:

Кусочно-постоянная функция
Кусочно-линейная функция
Кусочно-непрерывная функция

9. Построение графиков функций, содержащих модуль

f(x), если х≥0,
y= f(|x|)=
f(-x) , если х<0 .

10. Примеры задач на построение графиков из открытого банка заданий ОГЭ

11. Пример 1

y=x2−4|x|+2x
По определению модуля функция
y=x2−4|x|+2x распадается на две
функции:
y=x2−2x, если x > 0 и
y= f(x)=
y=x2+6x, если x < 0.

12. Пример 2

y=x2−|8x+1|
Функция y=x2−|8x+1| распадается на
две функции:
1
y=x2−8x–1, если х > - и
8
y= f(x)=
1
y=x2+8x+1, если х < 8

13. Пример 3

y=|x|(x+1)−6x
По определению модуля функция
y=|x|(x+1)−6x распадается на две
функции:
y = x2−5x, если x > 0,
y= f(x)=
y = - x2 −7x, если x < 0.

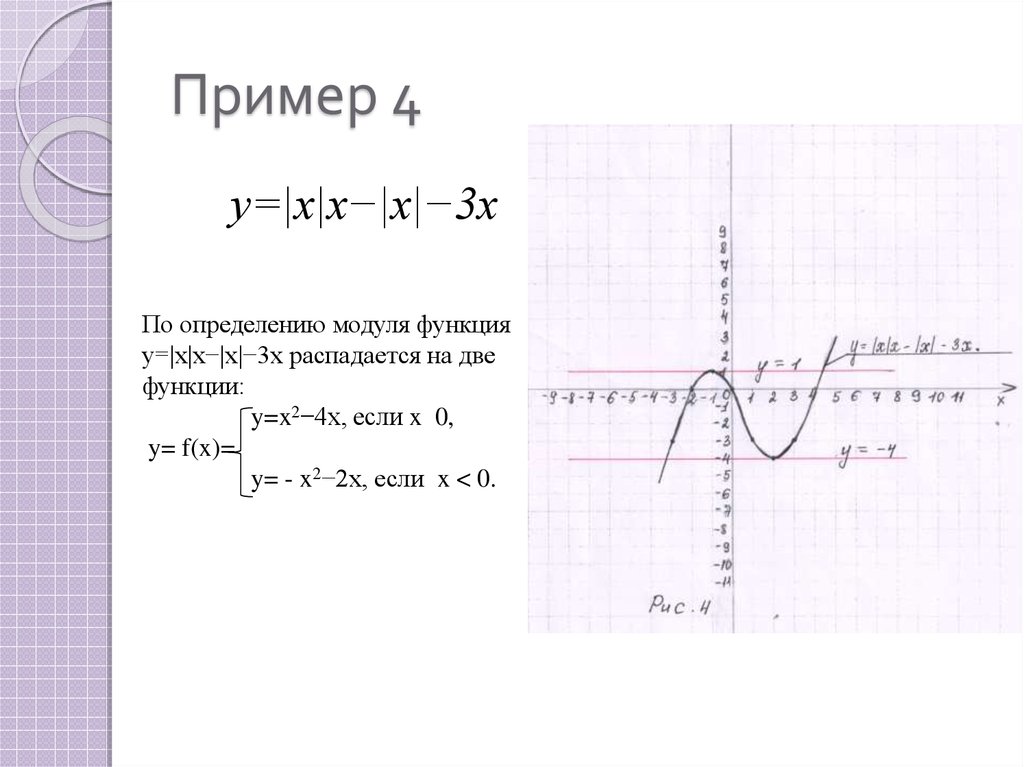
14. Пример 4

y=|x|x−|x|−3x
По определению модуля функция
y=|x|x−|x|−3x распадается на две
функции:
y=x2−4x, если x 0,
y= f(x)=
y= - x2−2x, если x < 0.

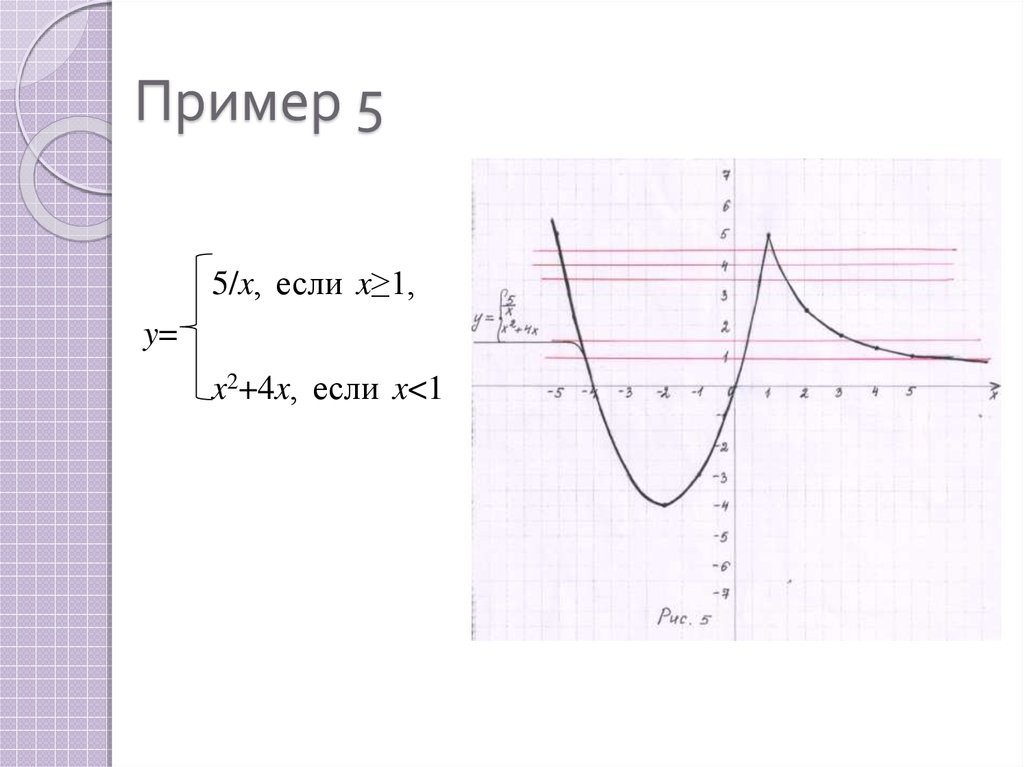
15. Пример 5

5/x,  если  x≥1,
y=
x2+4x,  если  x<1

16. Заключение

При исследовании темы были достигнуты следующие
результаты:
мы достаточно хорошо изучили теоретическую часть данной
темы;
систематизировали задания из ОБЗ;
выработали алгоритм построения графиков функций,
содержащих модуль ;
оформили презентацию.
Тем самым мы нашли подтверждение нашей гипотезе
о том, что если проследить закономерности в
решении задач, то можно составить алгоритм
действий.

17. Библиографический список:

1.
2.
3.
4.
5.
С.М.Никольский, М.К.Потапов,
Н.Н.Решетников,А.В.Шевкин. Алгебра.: Учебник для 8
класса общеобразовательной школы.- М. :Просвещение,
2014.-301 стр
Потапов М.К., Александров В.В., Пасиченко П.И. Алгебра и
анализ элементарных функций, - Москва «Наука», 1981, 560
стр.
Энциклопедический словарь юного математика./ Под
ред.Гнеденко Б.В., -М. «Педагогика»1985, 345 стр.
ru.wikipedia.org
http://fipi.ru/content/otkrytyy-bank-zadaniy-oge