Similar presentations:
Устойчивость состояния. Устойчивость движения
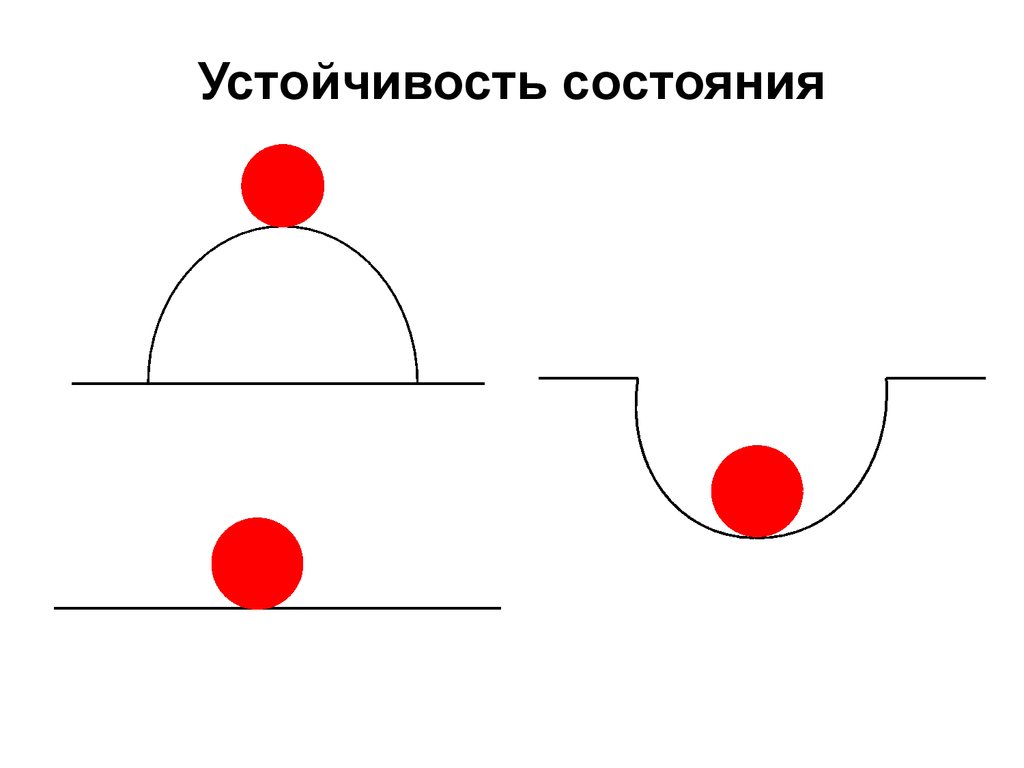
1. Устойчивость состояния
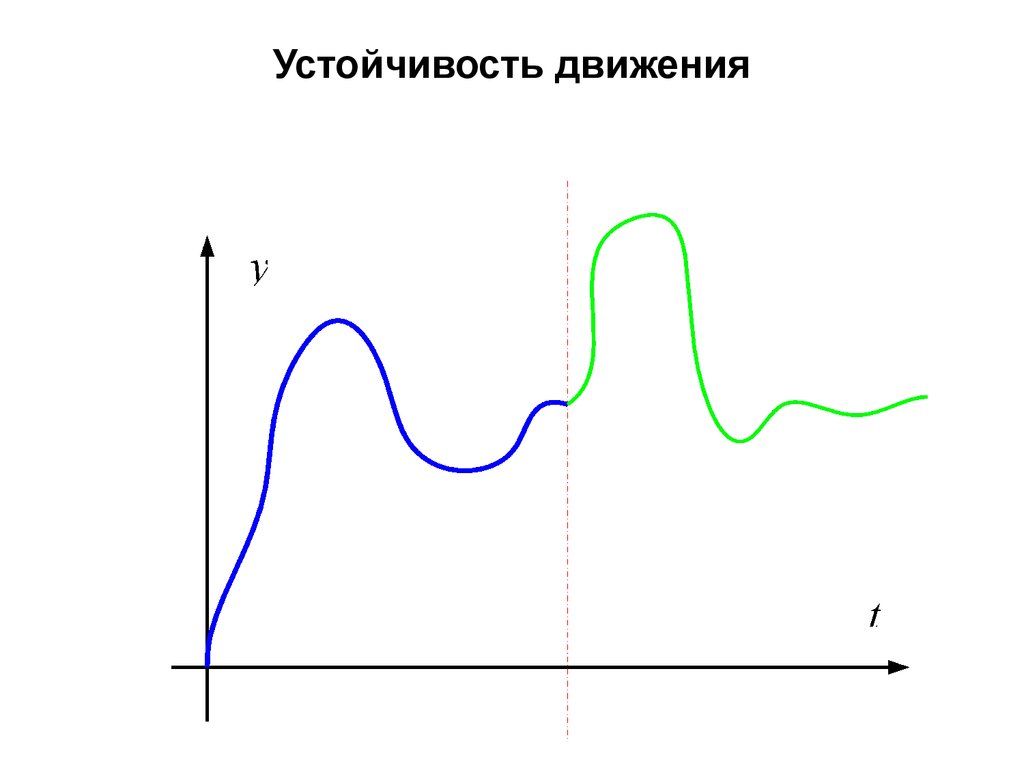
2. Устойчивость движения
3. Устойчивость движения
4. Устойчивость движения
5.
nn -1
d y (t )
d y (t )
a0
+ a1
+ K + an y (t ) =
n
n -1
dt
dt
m
m -1
d x(t )
d x(t )
= b0
+
b
+
K
+
b
x
(
t
)
1
m
dt m
dt m -1
y (t ) = yобщ (t ) + yчаст (t )
y (t ) = yсв (t ) + yвын (t )
6. Устойчивость по Ляпунову
lim yсв (tСАУ) = 0 уст
-
t ®¥
lim yсв (tСАУ
) ® ¥неуст
-
t ®¥
¹0
lim yсв (tСАУ
)
на-границе уст
t ®¥
¹¥
.
.
7. Связь корней характеристического уравнения с устойчивостью
nn -1
n
n -1
d y (t )
d y (t )
a0
+ a1
+ K + an y (t ) = 0
n
n -1
dt
dt
a0 p y ( p ) + a1 p
y ( p ) + K + an y ( p ) = 0
n
yсв (t ) = å Ci e
i =1
pi t
8.
piсв= -ai
y i (t ) = C e
-a t
9.
piсв= +ai
y i (t ) = C e
+a t
10.
pi = -a ± j byсвi (t ) = Ci e
( -a ± j b ) t
= Ci e
-a t
sin( b t )
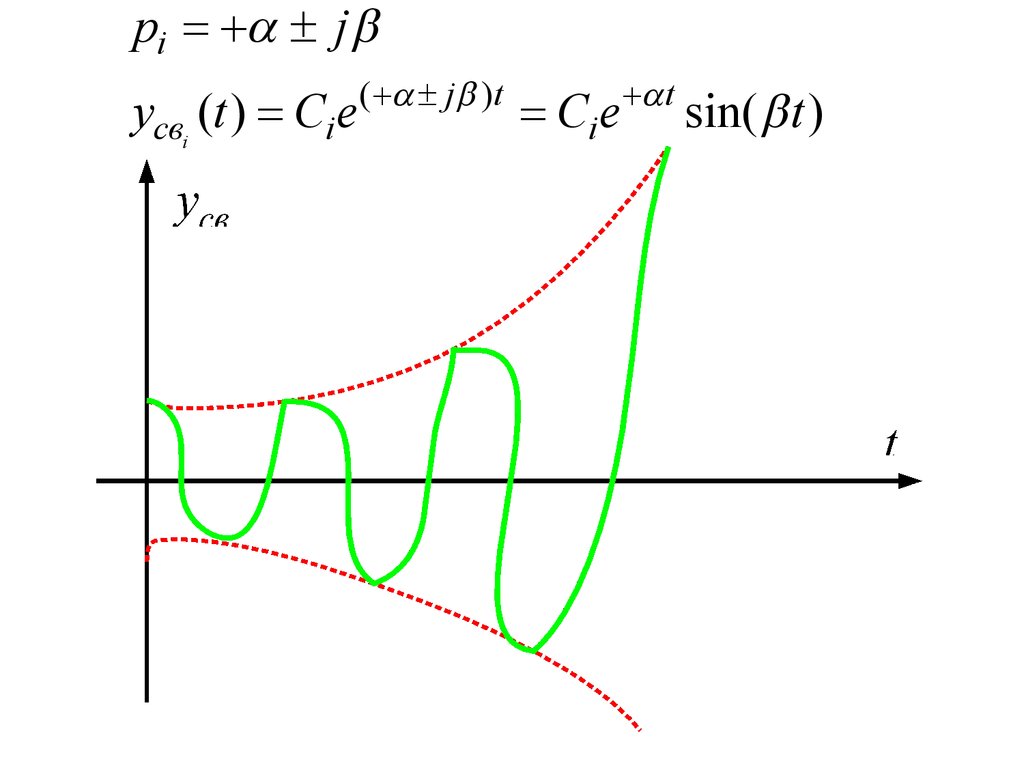
11.
pi = +a ± j byсвi (t ) = Ci e
( +a ± j b ) t
= Ci e
+a t
sin( b t )
12.
pi = ± j byсвi (t ) = Ci e
± jb t
= Ci sin( b t )
13.
pi = 00t
yсвi (t ) = Ci e = Ci











 mathematics
mathematics








