Similar presentations:
Усеченная пирамида
1.
2. Содержание
1. Исторические сведения2. Выдающиеся личности
3. Литературные высказывания
4. Объяснение материала
4.1 Определения
4.2 Виды
4.3 Элементы
4.4 Сечения
4.5 Площадь:
4.5.1 Основание
4.5.2 Боковые поверхности
4.5.3 Площадь полной поверхности
4.6 Объем
4.7 Развертка усеченной пирамиды
5. Задачи
6. Применение
7. Обратная связь
8. Сказка
3. Исторические сведения
Началогеометрии пирамиды было положено в
Древнем Египте и Вавилоне, однако активное
развитие получило в Древней Греции. Объем
пирамиды был известен древним египтянам.
Пирамида Чичен - Ица
Египетские пирамиды
4. Выдающиеся личности
Первым греческим математиком, ктоустановил, чему равен объём пирамиды,
был Демокрит , а доказал Евдокс Книдский
5.
Древнегреческийматематик Евклид систематизировал знания о
пирамиде в XII томе своих «Начал», а также вывел
первое определение пирамиды: телесная фигура,
ограниченная плоскостями, которые от одной
плоскости сходятся в одной точке
6. высказывания про пирамиду
Общественнаяжизнь, по сути – одновременно
глупая и хитря финансовая пирамида.
Во властной пирамиде, так же как и в пищевой,
жирное и сладкое располагается наверху.
7.
Египтяне их сложилиИ так ловко смастерили,
Что стоят они веками.
Догадайтесь, дети, сами
Что же это за тела,
Где вершина всем видна?
Догадались? Из – за вида
Всем известна…
8. Объяснение материала
9. Определение усеченной пирамиды
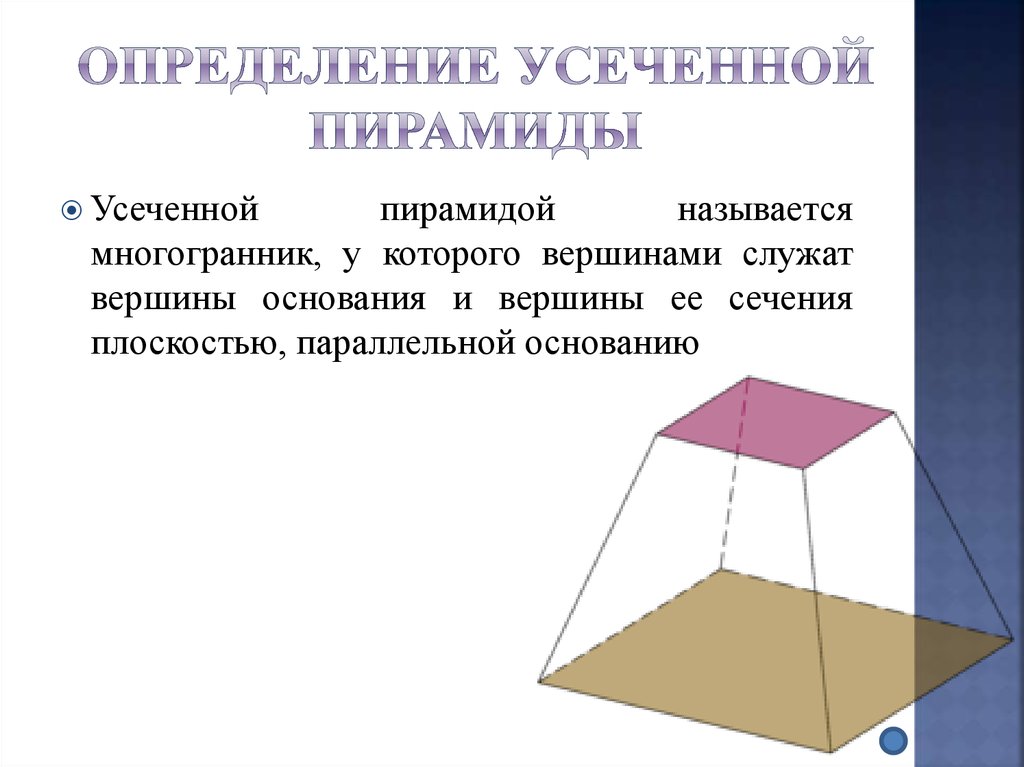
Усеченнойпирамидой
называется
многогранник, у которого вершинами служат
вершины основания и вершины ее сечения
плоскостью, параллельной основанию
10.
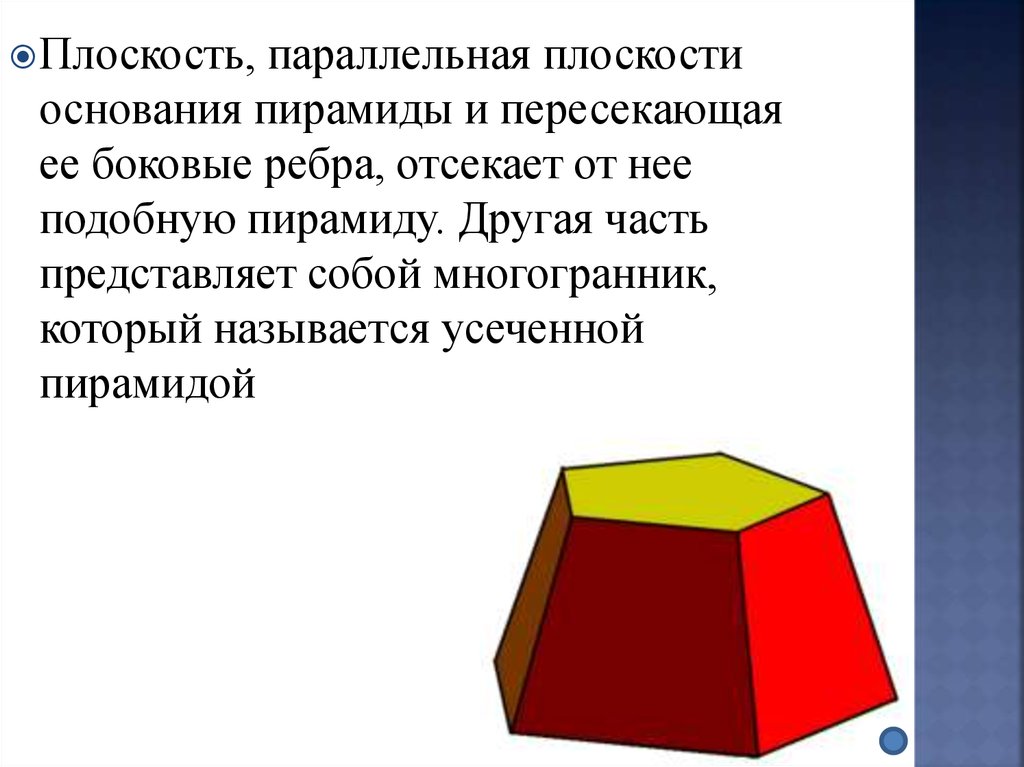
Плоскость,параллельная плоскости
основания пирамиды и пересекающая
ее боковые ребра, отсекает от нее
подобную пирамиду. Другая часть
представляет собой многогранник,
который называется усеченной
пирамидой
11.
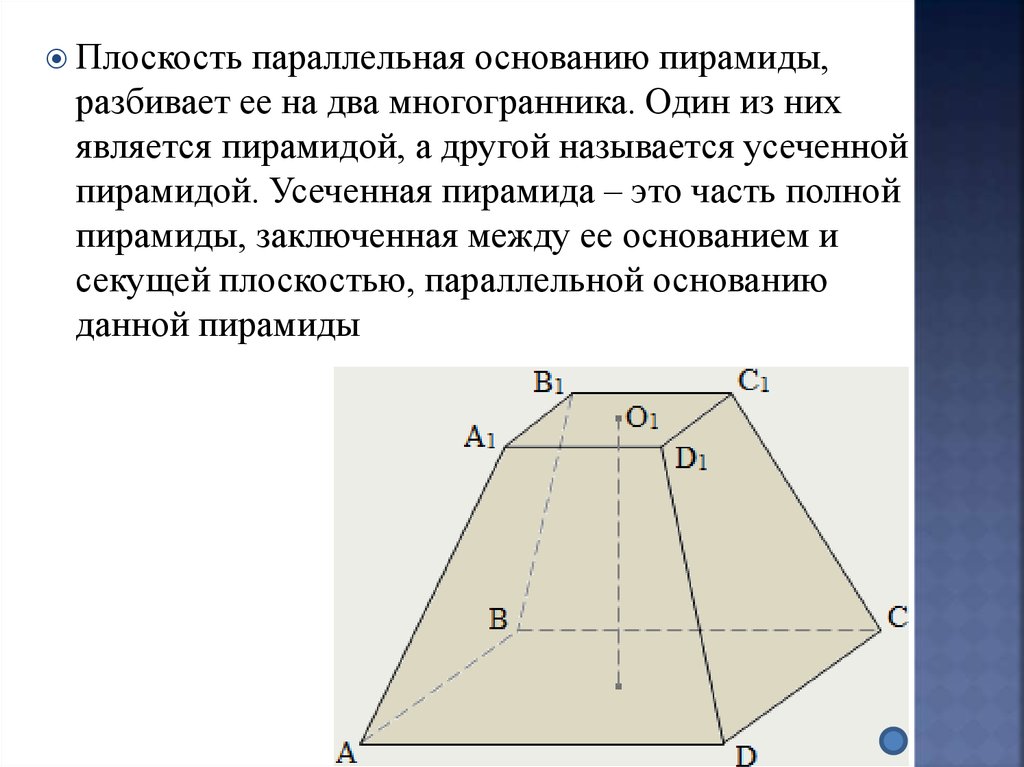
Плоскостьпараллельная основанию пирамиды,
разбивает ее на два многогранника. Один из них
является пирамидой, а другой называется усеченной
пирамидой. Усеченная пирамида – это часть полной
пирамиды, заключенная между ее основанием и
секущей плоскостью, параллельной основанию
данной пирамиды
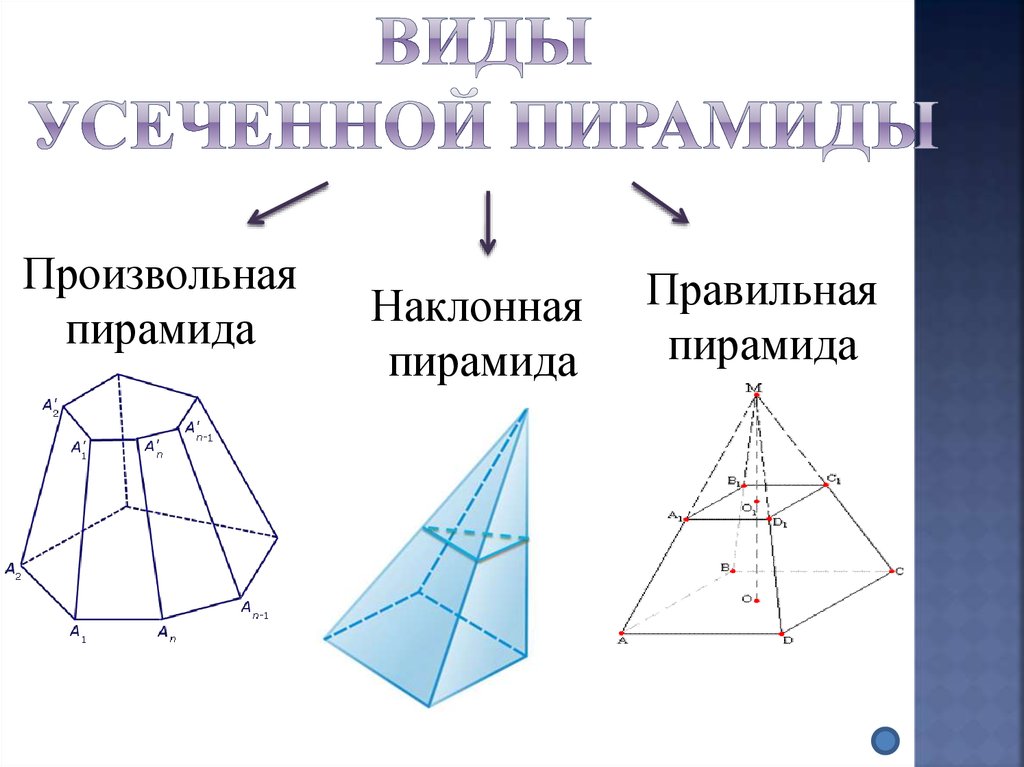
12. Виды усеченной пирамиды
Произвольнаяпирамида
Наклонная
пирамида
Правильная
пирамида
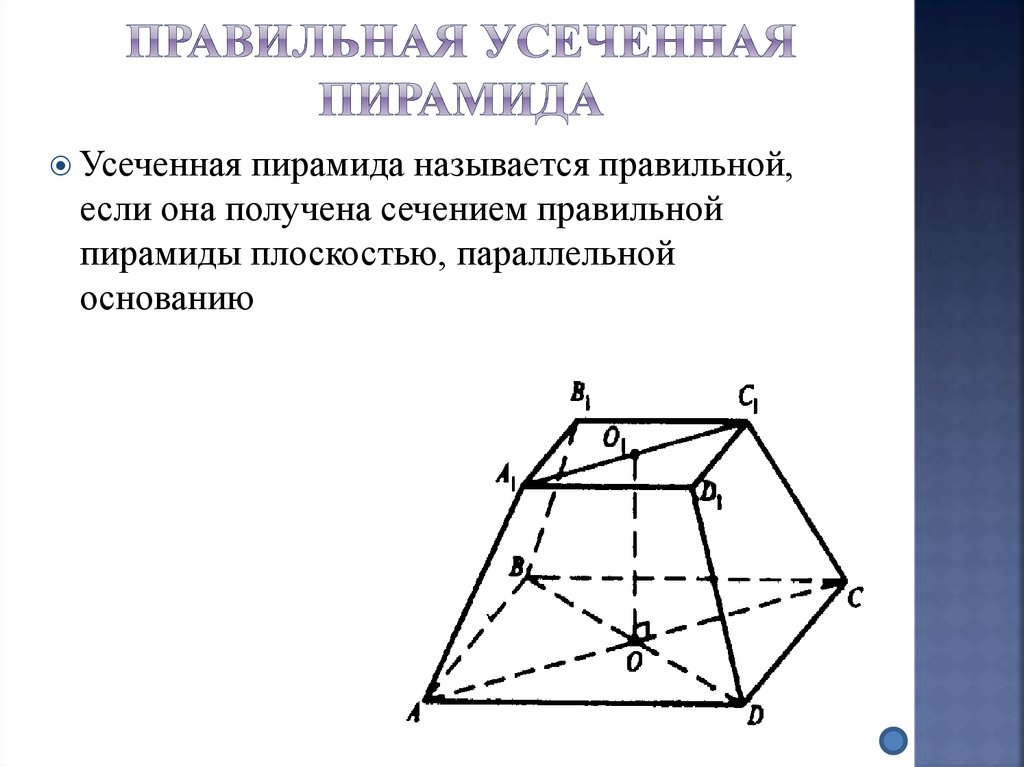
13. Правильная усеченная пирамида
Усеченнаяпирамида называется правильной,
если она получена сечением правильной
пирамиды плоскостью, параллельной
основанию
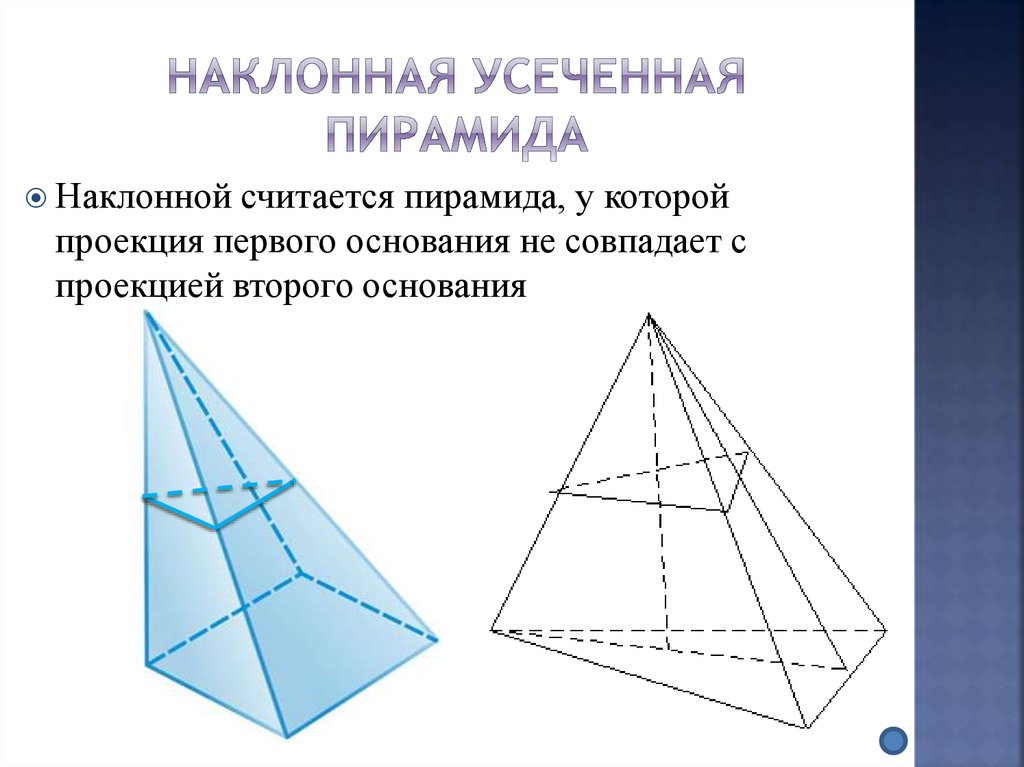
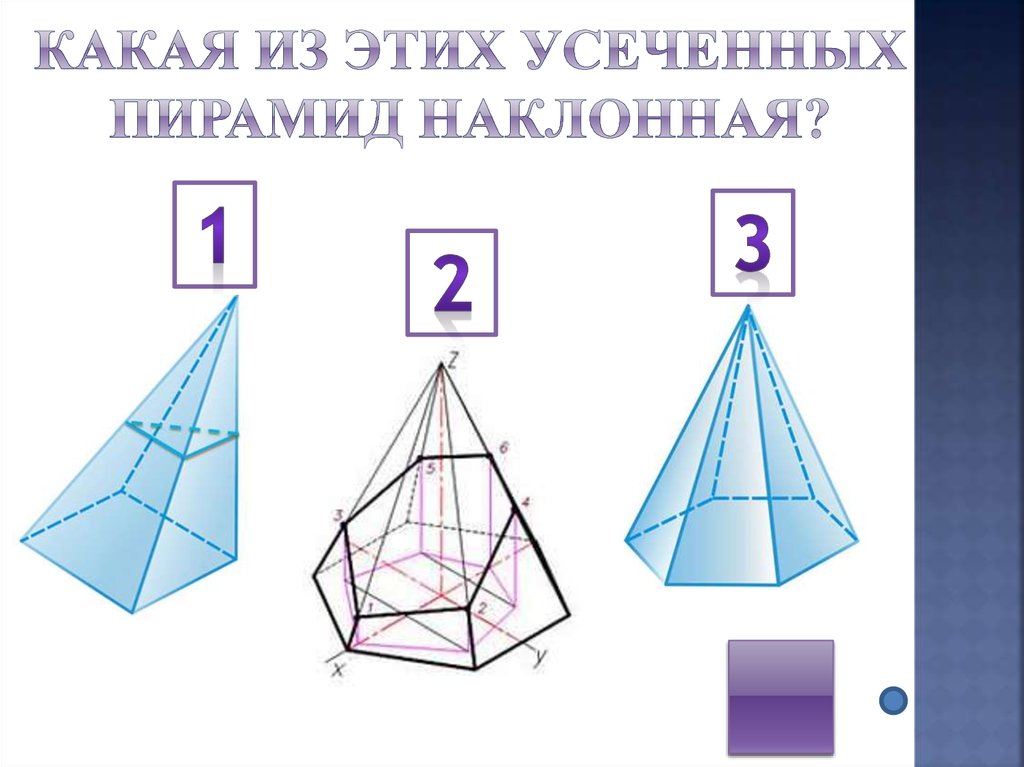
14. Наклонная усеченная пирамида
Наклоннойсчитается пирамида, у которой
проекция первого основания не совпадает с
проекцией второго основания
15. Элементы усеченной пирамиды
16. 1. Основание усеченной пирамиды
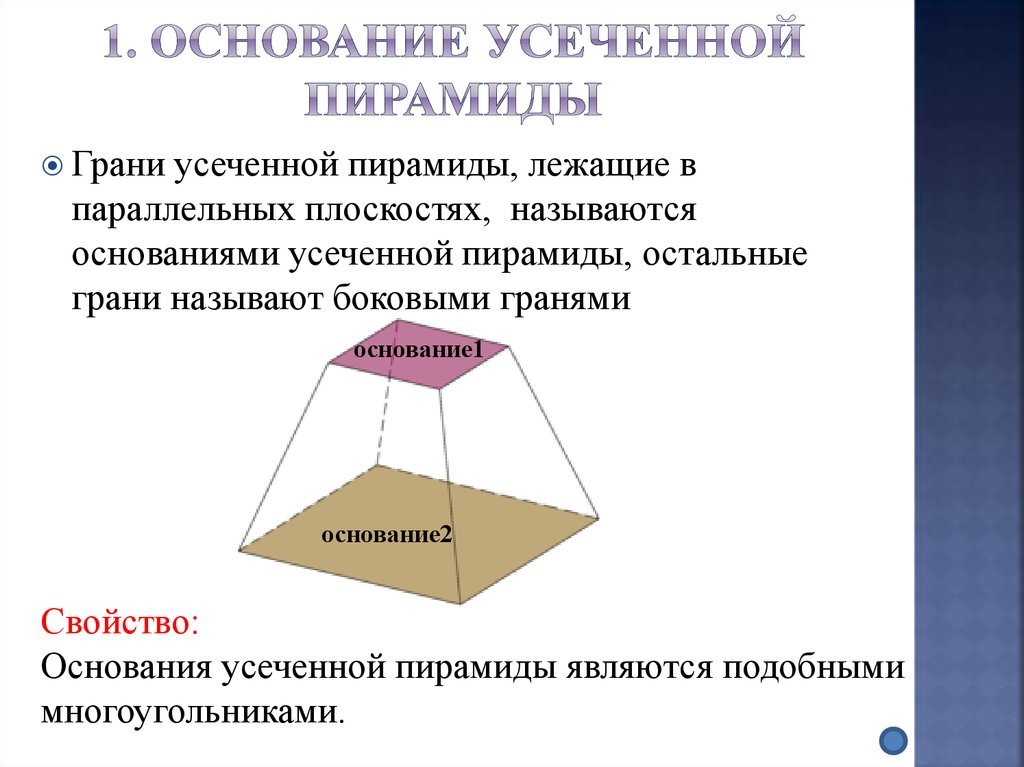
Граниусеченной пирамиды, лежащие в
параллельных плоскостях, называются
основаниями усеченной пирамиды, остальные
грани называют боковыми гранями
основание1
основание2
Свойство:
Основания усеченной пирамиды являются подобными
многоугольниками.
17. 2. Боковые Грани усеченной пирамиды
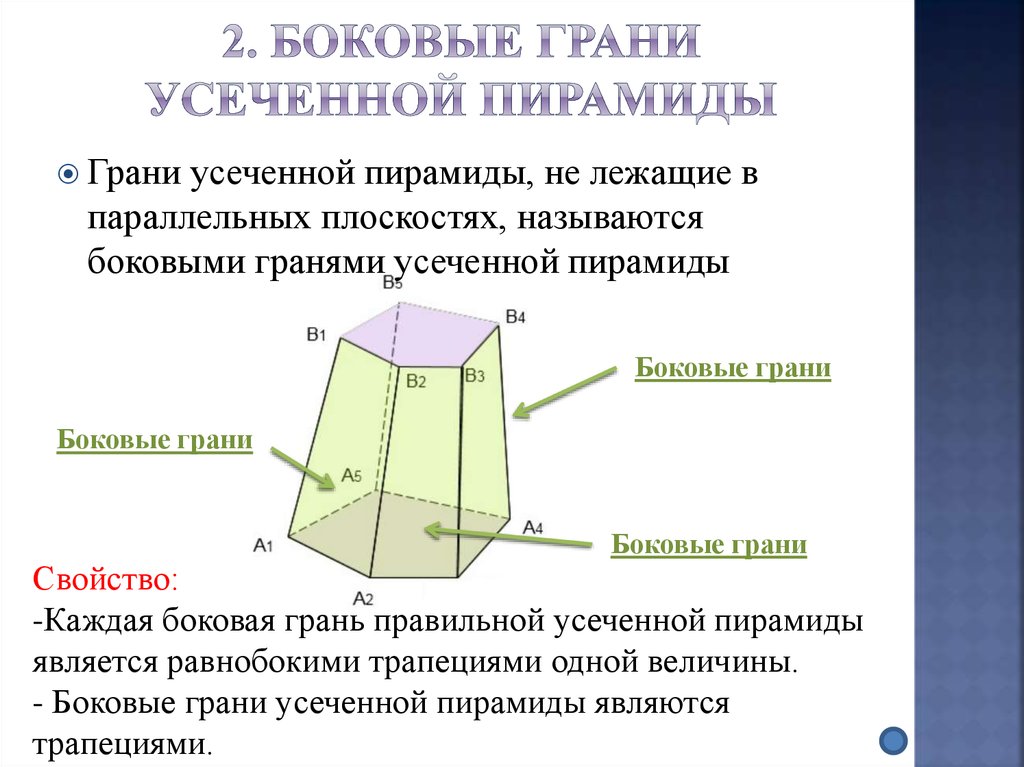
Граниусеченной пирамиды, не лежащие в
параллельных плоскостях, называются
боковыми гранями усеченной пирамиды
Боковые грани
Боковые грани
Боковые грани
Свойство:
-Каждая боковая грань правильной усеченной пирамиды
является равнобокими трапециями одной величины.
- Боковые грани усеченной пирамиды являются
трапециями.
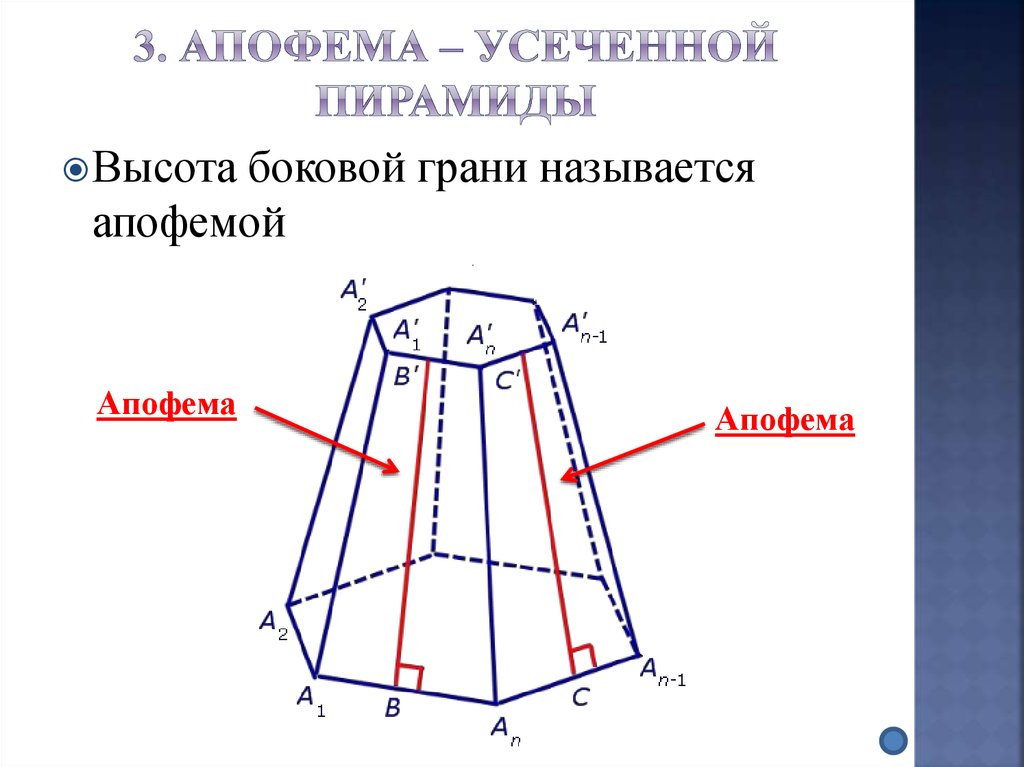
18. 3. Апофема – усеченной пирамиды
Высотабоковой грани называется
апофемой
Апофема
Апофема
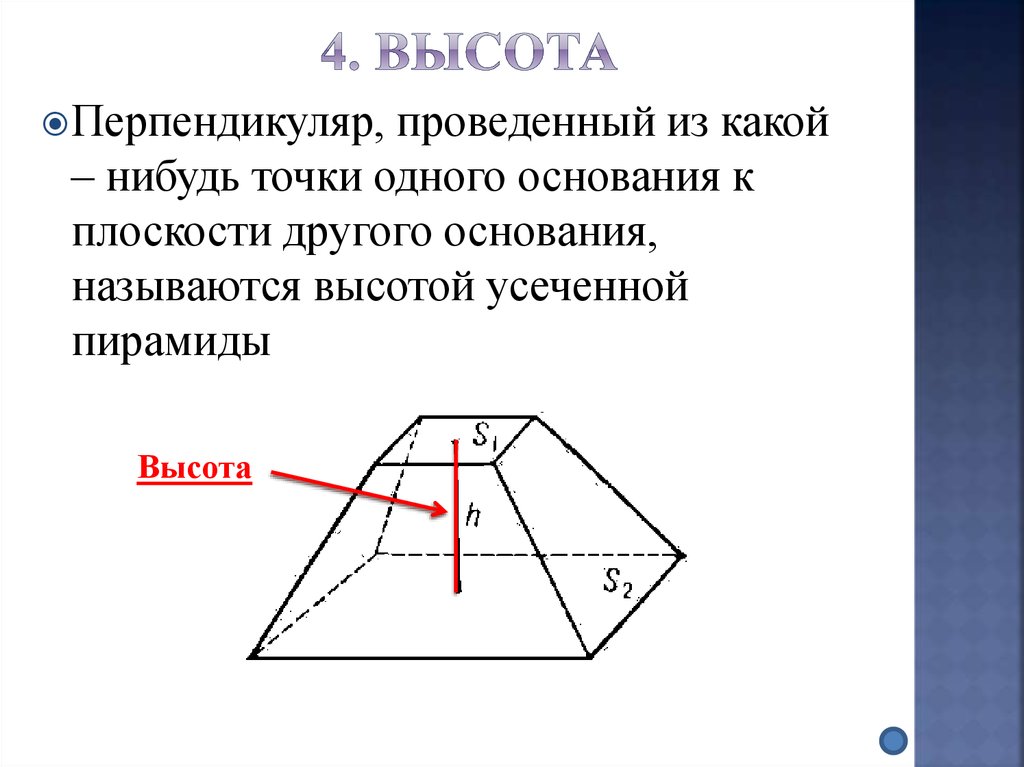
19. 4. Высота
Перпендикуляр,проведенный из какой
– нибудь точки одного основания к
плоскости другого основания,
называются высотой усеченной
пирамиды
Высота
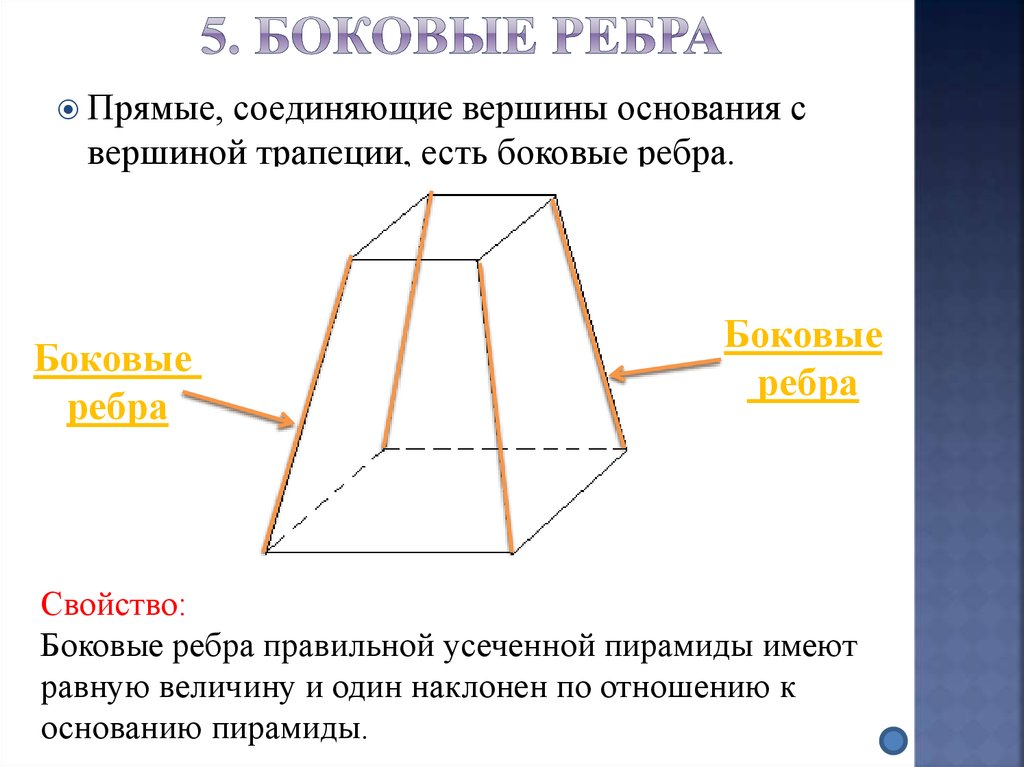
20. 5. Боковые ребра
Прямые,соединяющие вершины основания с
вершиной трапеции, есть боковые ребра.
Боковые
ребра
Боковые
ребра
Свойство:
Боковые ребра правильной усеченной пирамиды имеют
равную величину и один наклонен по отношению к
основанию пирамиды.
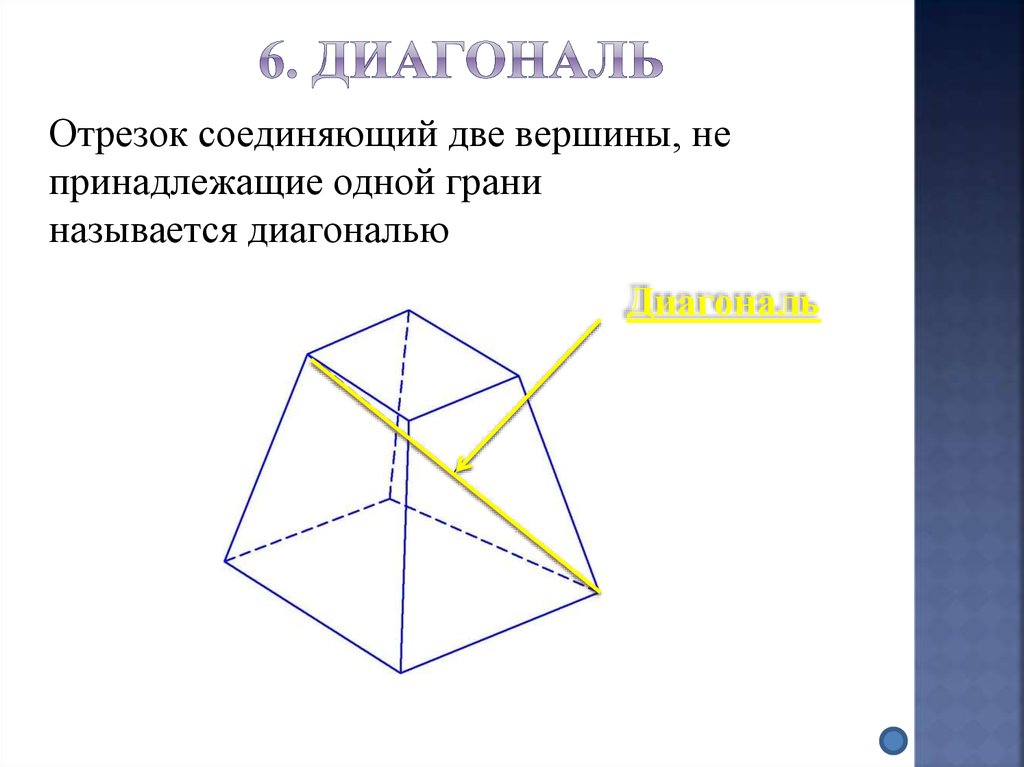
21. 6. диагональ
Отрезок соединяющий две вершины, непринадлежащие одной грани
называется диагональю
Диагональ
22. Сечения усеченной пирамиды
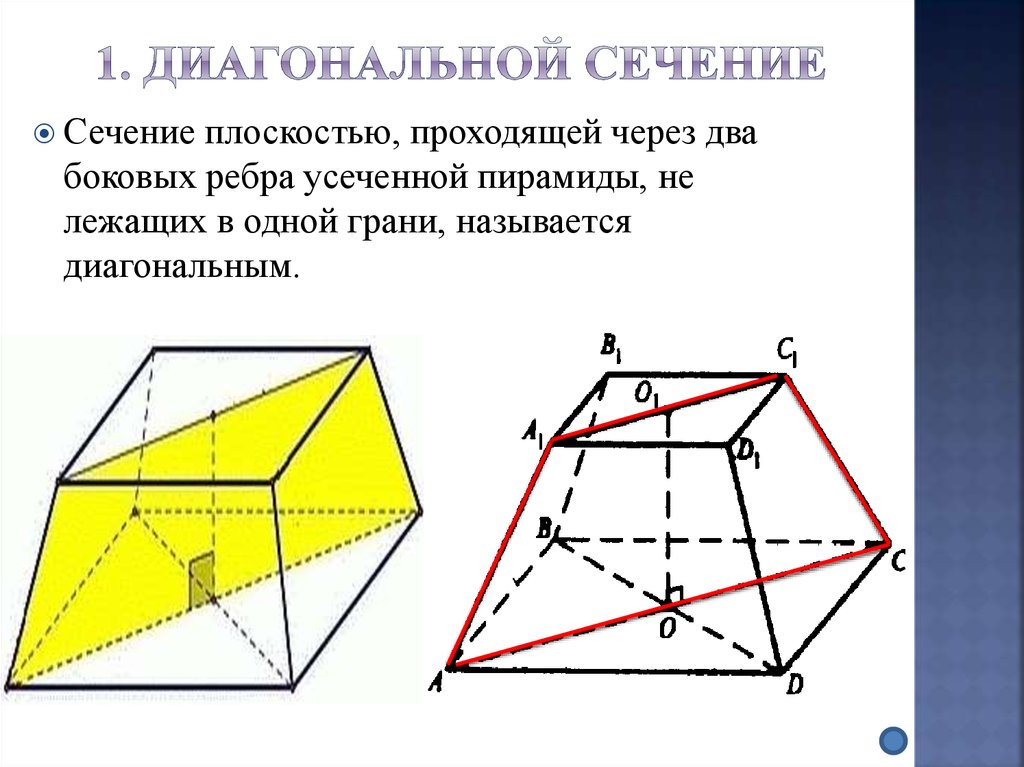
23. 1. Диагональной сечение
Сечениеплоскостью, проходящей через два
боковых ребра усеченной пирамиды, не
лежащих в одной грани, называется
диагональным.
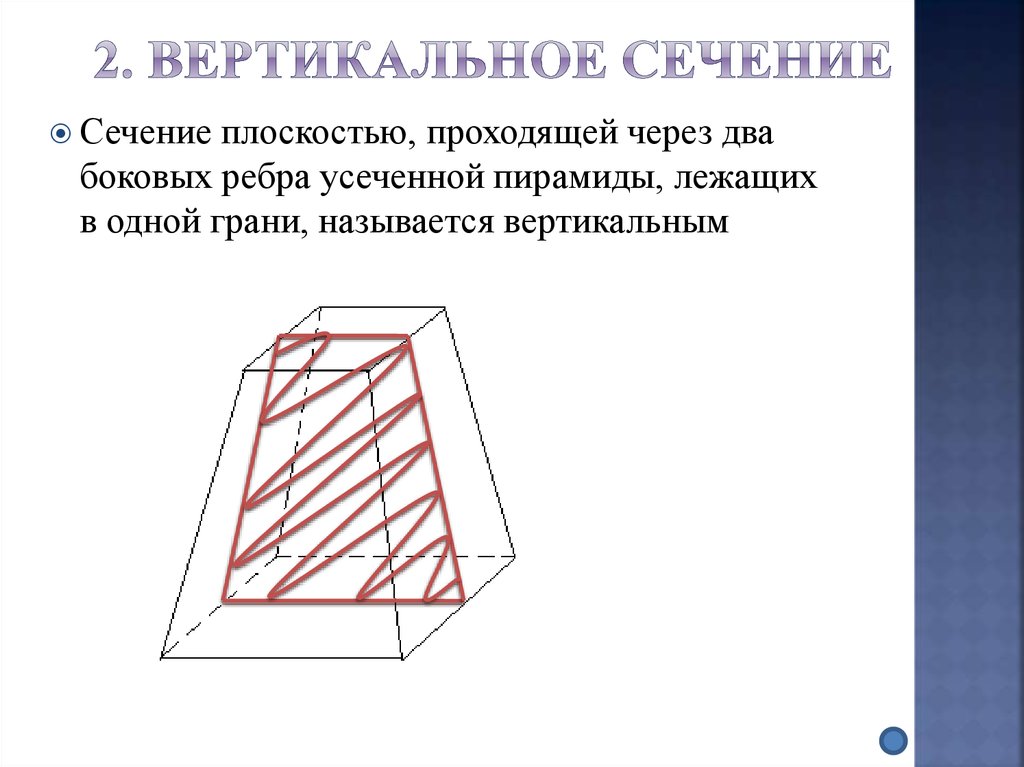
24. 2. Вертикальное сечение
Сечениеплоскостью, проходящей через два
боковых ребра усеченной пирамиды, лежащих
в одной грани, называется вертикальным
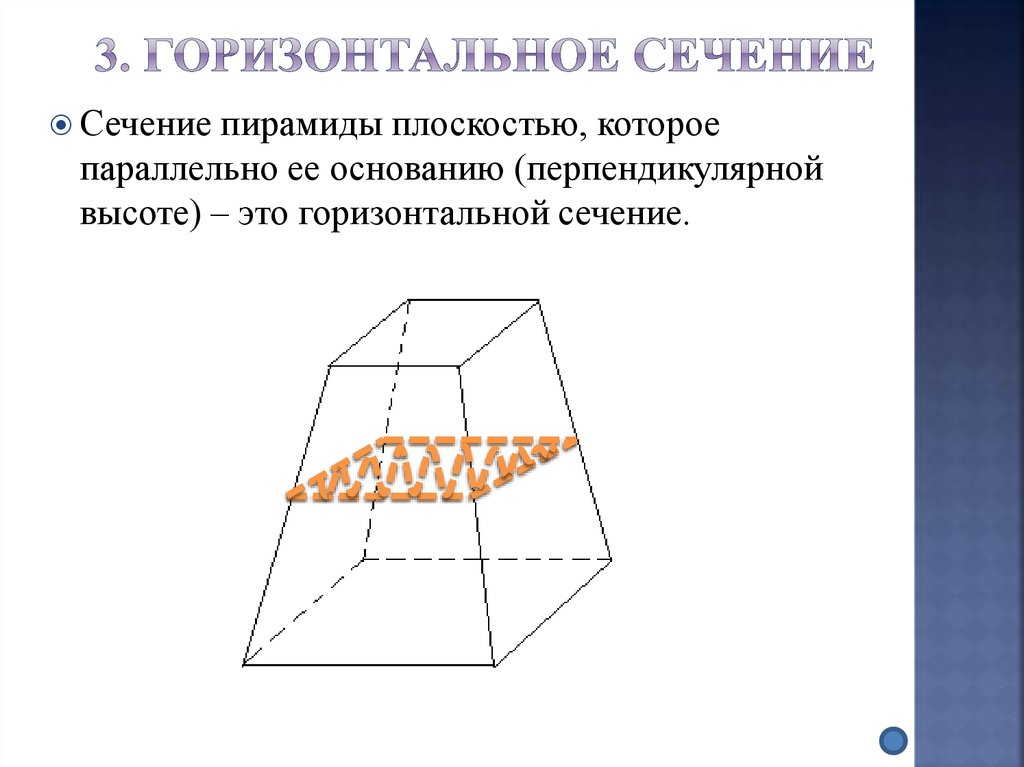
25. 3. Горизонтальное сечение
Сечениепирамиды плоскостью, которое
параллельно ее основанию (перпендикулярной
высоте) – это горизонтальной сечение.
26. Вычисление площадей усеченной пирамиды
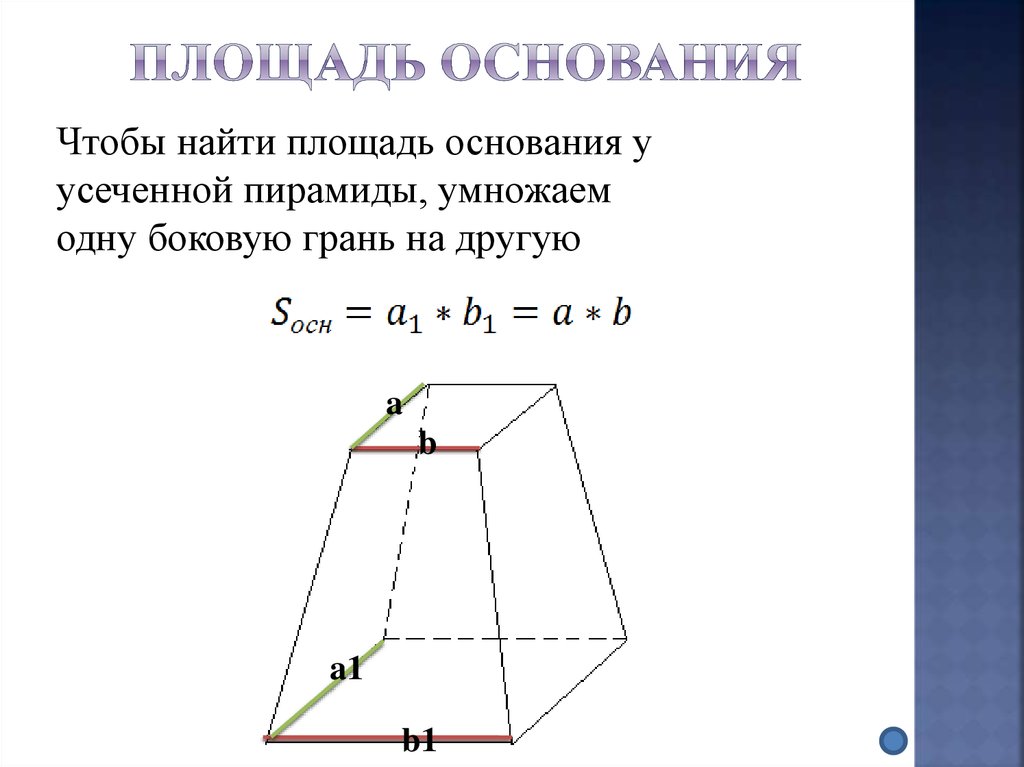
27. Площадь основания
Чтобы найти площадь основания уусеченной пирамиды, умножаем
одну боковую грань на другую
a
b
a1
b1
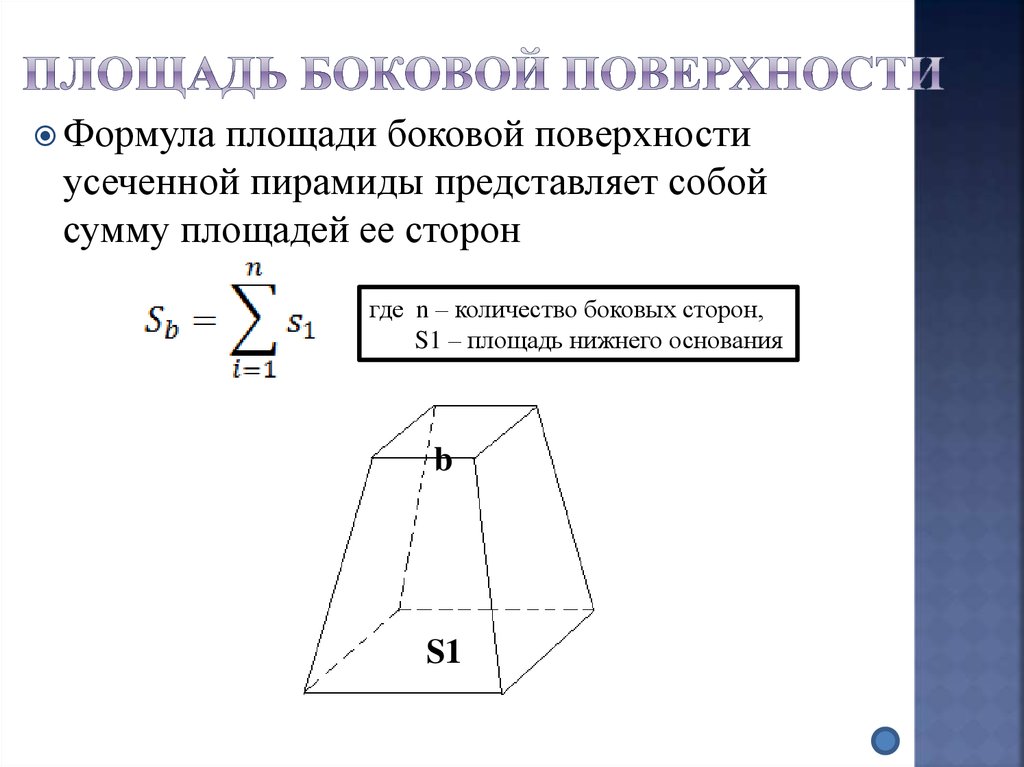
28. Площадь боковой поверхности
Формулаплощади боковой поверхности
усеченной пирамиды представляет собой
сумму площадей ее сторон
где n – количество боковых сторон,
S1 – площадь нижнего основания
b
S1
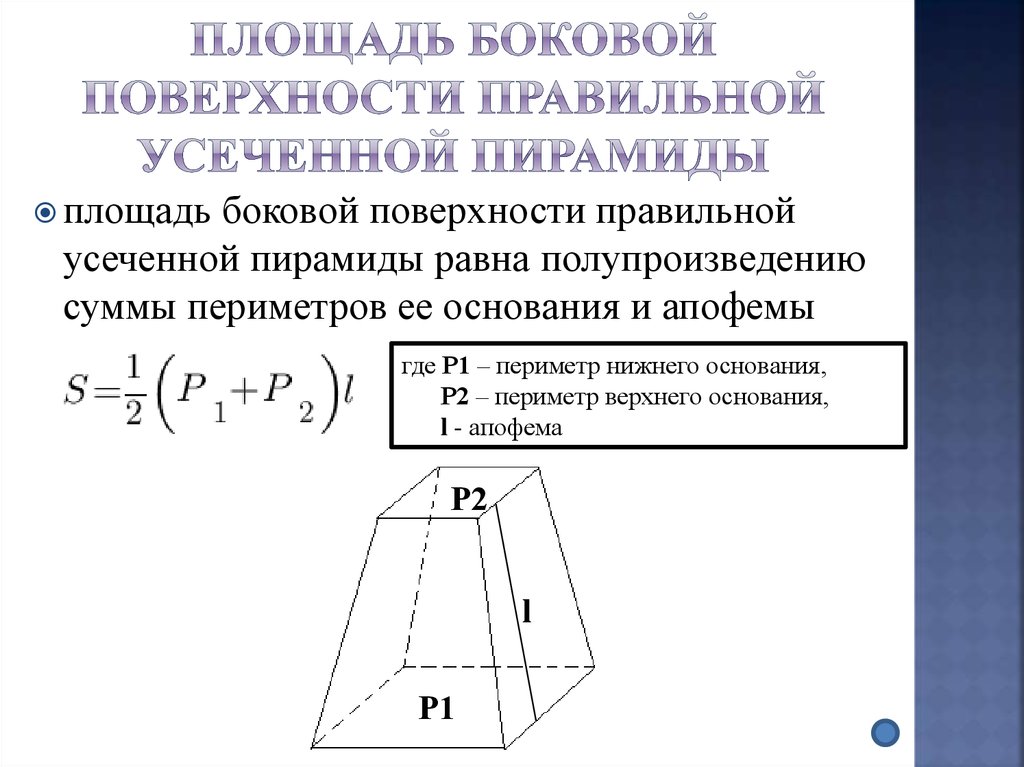
29. Площадь боковой поверхности ПРАВИЛЬНОЙ УСЕЧЕННОЙ ПИРАМИДЫ
площадьбоковой поверхности правильной
усеченной пирамиды равна полупроизведению
суммы периметров ее основания и апофемы
где Р1 – периметр нижнего основания,
Р2 – периметр верхнего основания,
l - апофема
Р2
l
Р1
30. Площадь ПОЛНОЙ поверхности усеченной пирамиды
где S1 и S2 – площади основанийусеченной пирамиды,
Sбок – площадь боковой поверхности
усеченной поверхности
S2
Sбок
S1
31. Объем усеченной пирамиды
где Н – длина высоты усеченной пирамиды,S1 и S2 - площади оснований
S2
Н
S1
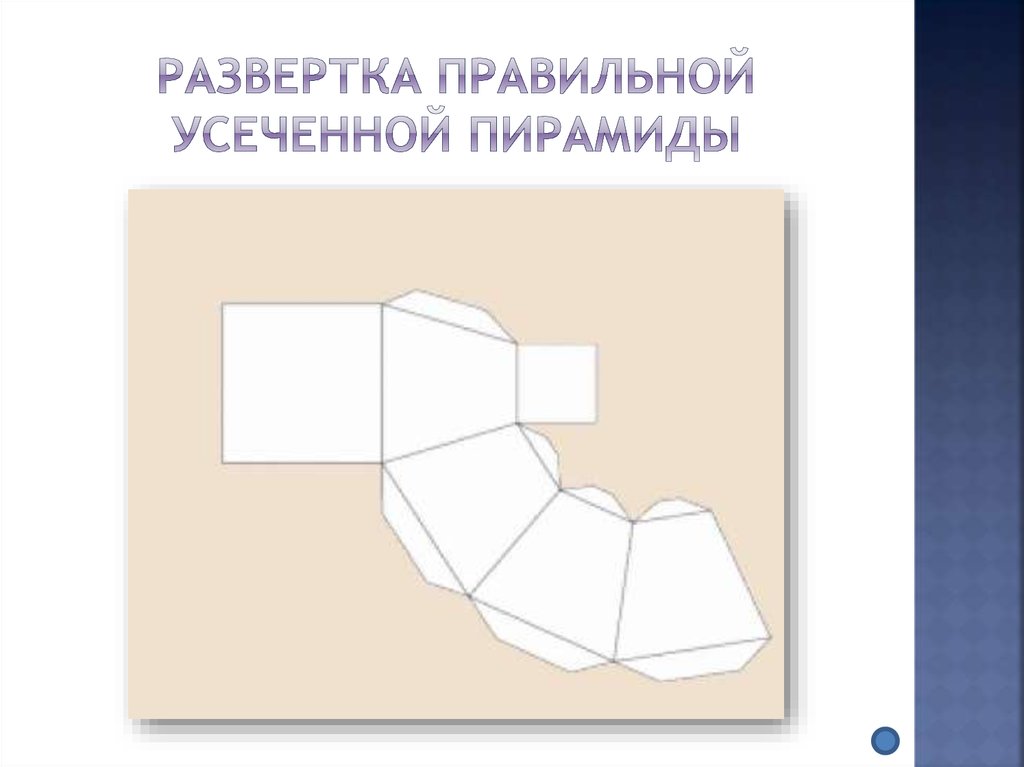
32. Развертка правильной усеченной пирамиды
33. Задача №1
34.
35.
36.
37.
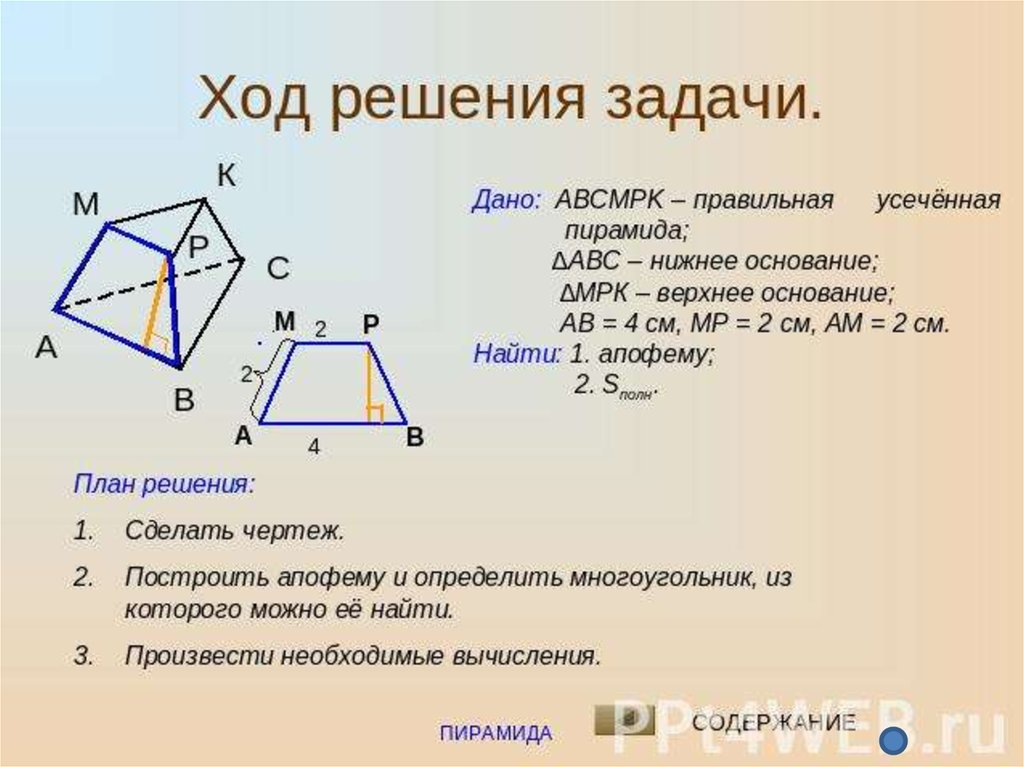
38. Задача №2
39.
Высотаправильной четырехугольной
усеченной пирамиды равен 3 м, стороны
оснований 5 м и 1 м. Найти объем
пирамиды.
Дано:
H=3м,
а=1м,
b=5м
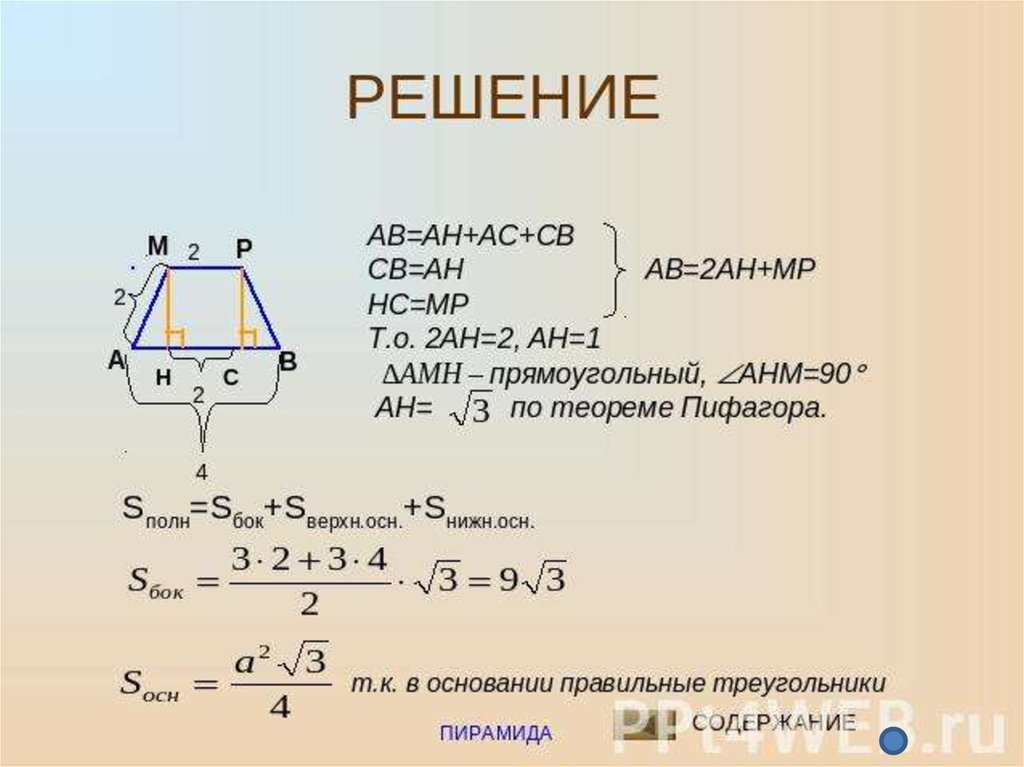
Решение:
Находим сначала площадь S1 и S2,
т.к. усеченная пирамида правильная,
Найти: V-?
находим площадь по формуле
S=

































 mathematics
mathematics








