Similar presentations:
Системы линейных уравнений
1. Системы линейных уравнений
Элементы высшей математикиЛинейная алгебра
2. Система линейных алгебраических уравнений
содержащаяm уравнений
n неизвестных
3. Система из 3 уравнений с 3 неизвестными
Система линейныхалгебраических уравнений
СЛАУ
4. Матрица системы
Расширенная матрица системы5. Столбец неизвестных
Столбец свободных членов6. Совместная система
СЛАУ, которая имеет хотя бы однорешение
Несовместная система
Не имеет решений
7. Теорема Кронекера-Капелли
СЛАУ совместна ранграсширенной матрицы
системы равен рангу
основной матрицы системы
8. Теорема
Если ранг совместной системыравен числу неизвестных, то
система имеет единственное
решение
rang(A) = n
9. Теорема
Если ранг совместной системыменьше числа неизвестных, то
система имеет бесчисленное
множество решений
rang(A) < n
10. Метод обратной матрицы
МЕТОД ОБРАТНОЙМАТРИЦЫ
11. Матричный метод
12. Метод Крамера
МЕТОД КРАМЕРА13. Габриэль Крамер
Швейцарскийматематик
Один из создателей
линейной алгебры
1704 1752
14. Формулы Крамера
Определитель матрицы системы15. Дополнительные определители
Столбец коэффициентов присоответствующей неизвестной
заменяется столбцом
свободных членов системы
16. Формулы Крамера
17. Формулы Крамера
18. Формулы Крамера
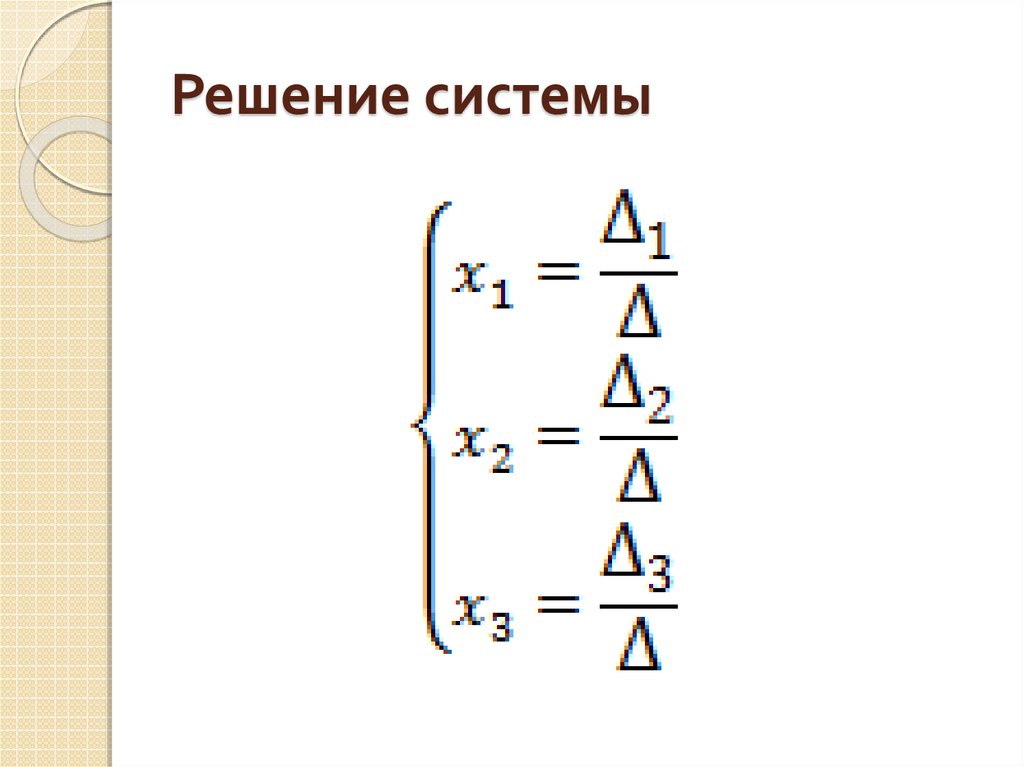
19. Решение системы
20. Метод гаусса
МЕТОД ГАУССА21. Иоганн Карл Фридрих Гаусс
Немецкийматематик, механик,
физик, астроном и
геодезист
1777 1855
«Король
математики»
22. Теорема о приведении матриц к ступенчатому виду
Любую матрицу путёмэлементарных преобразований
только над строками можно
привести к ступенчатому виду
23. Метод Гаусса
Метод последовательногоисключения переменных
с помощью элементарных
преобразований СЛАУ приводится
к равносильной системе
треугольного вида
из неё последовательно, начиная с
последних, находятся все
переменные системы
24. Прямой ход
Элементарнымипреобразованиями над строками
систему приводят к ступенчатой
или треугольной форме,
либо устанавливают, что система
несовместна
25. Обратный ход
Находим значения переменных,начиная с последнего уравнения
26. Достоинства
Менее трудоёмкийПозволяет установить
совместность
Позволяет найти ранг
матрицы




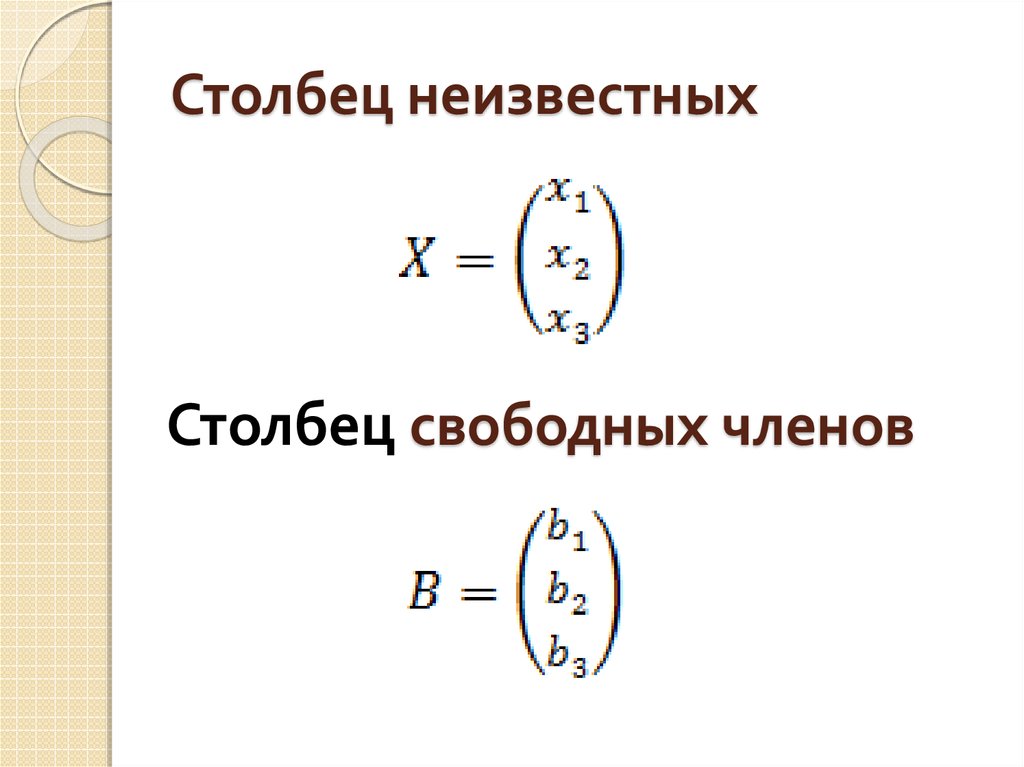




















 mathematics
mathematics








