Similar presentations:
Пересечение поверхности плоскостью
1.
ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТИПЛОСКОСТЬЮ
2.
Линия пересечения поверхности с плоскостью являетсялинией, одновременно принадлежащей поверхности
и секущей плоскости
Поэтому для ее построения необходимо отыскать такие
точки и линии, которые одновременно принадлежат
данной поверхности и заданной секущей плоскости
Замкнутая фигура, образованная линией пересечения
поверхности тела секущей плоскостью, называется
сечением
3.
Пересечение проецирующей поверхностис проецирующей плоскостью
4.
Прямой круговой цилиндр занимаетгоризонтально проецирующее положение
5.
12Секущая плоскость – горизонтально
проецирующая
П3
П2; П1
Ф
13
11
k2 (kI2)
kI3
k3
kI1
Ф
kI
k
k1
kI
k
Пара
прямых
Ф=k, kI
6.
Секущая плоскость фронтально- проецирующаяβ П2;
Ф
t2
t3
β3
t1
β1
β
t
t
эллипс
β Ф=t
7.
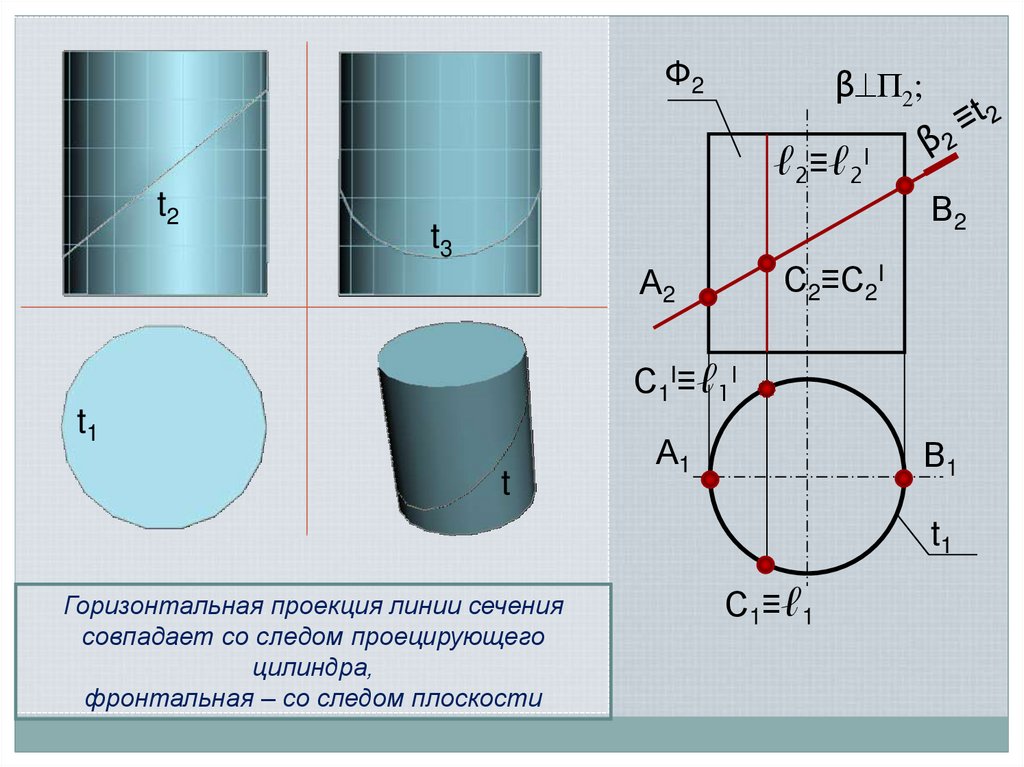
Ф2β П2;
ℓ2≡ℓ2I
t2
В2
t3
С2≡С2I
А2
С1I≡ℓ1I
t1
t
А1
В1
t1
Горизонтальная проекция линии сечения
совпадает со следом проецирующего
цилиндра,
фронтальная – со следом плоскости
С1≡ℓ1
8.
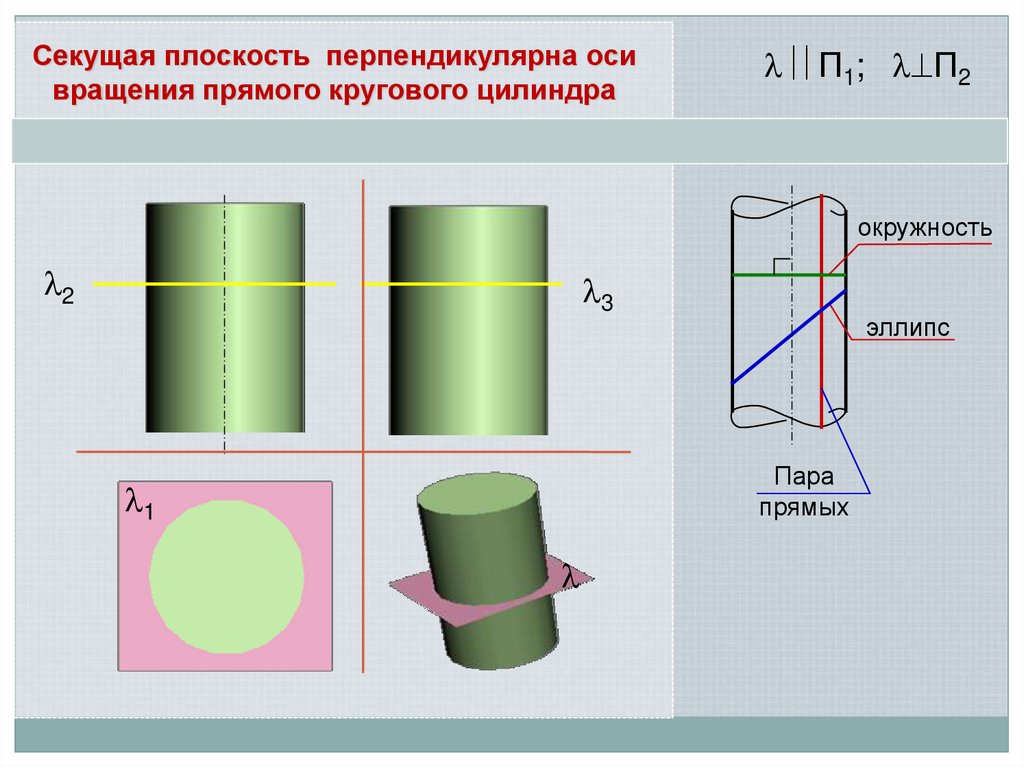
Секущая плоскость перпендикулярна осивращения прямого кругового цилиндра
П1; П2
окружность
2
3
эллипс
Пара
прямых
1
9.
Секущая плоскость фронтально –проецирующая
П2
Призма занимает горизонтально проецирующее положение
3
t2
f2
g2
k3
f1
k1
g1
k
1
k1
t1
10.
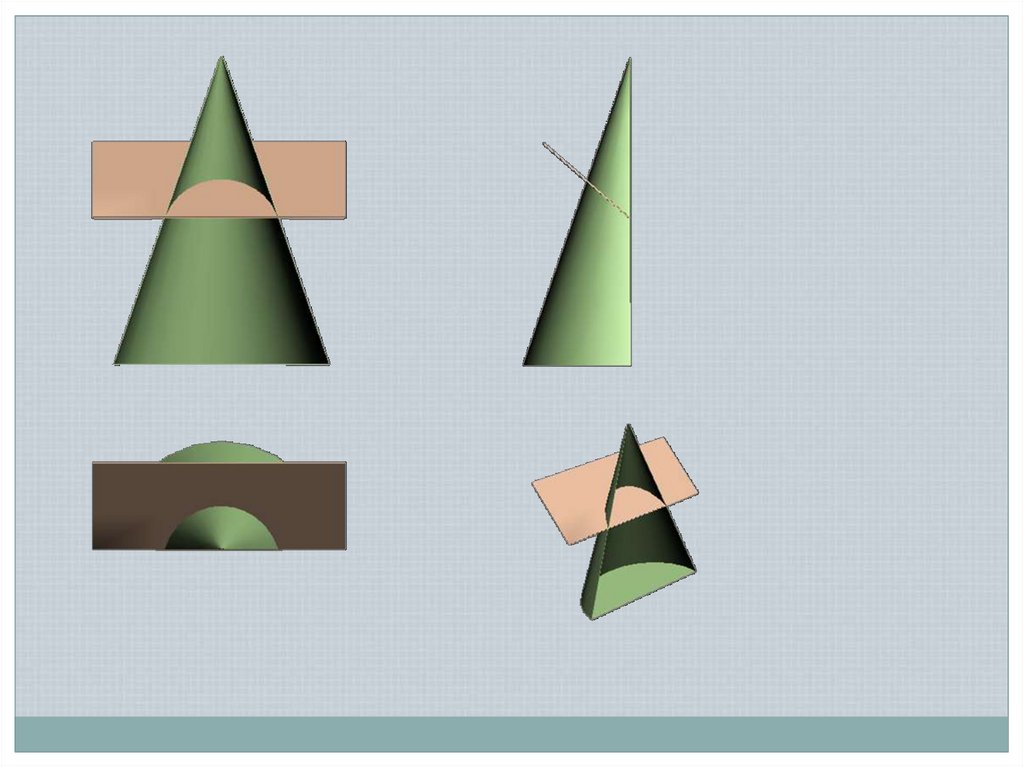
Пересечение поверхности общегоположения с проецирующей плоскостью
11.
Конические сечения(коники)
12.
Аполлоний прославился впервую очередь выдающейся
работой «Конические
сечения» (8 книг), в которой
дал содержательную общую
теорию эллипса, параболы и
гиперболы
Именно Аполлоний
предложил общепринятые Аполлоний Пергский
названия этих кривых; до него
262 год до н. э.
их называли просто
«сечениями конуса»
http://ru.wikipedia.org/wiki/Файл:Apollonios_of_Perga.jpeg
13.
Секущая плоскость перпендикулярнаоси вращения
12
А2
А1
11
А3
1
1
2 П1
точка
3
А
1
14.
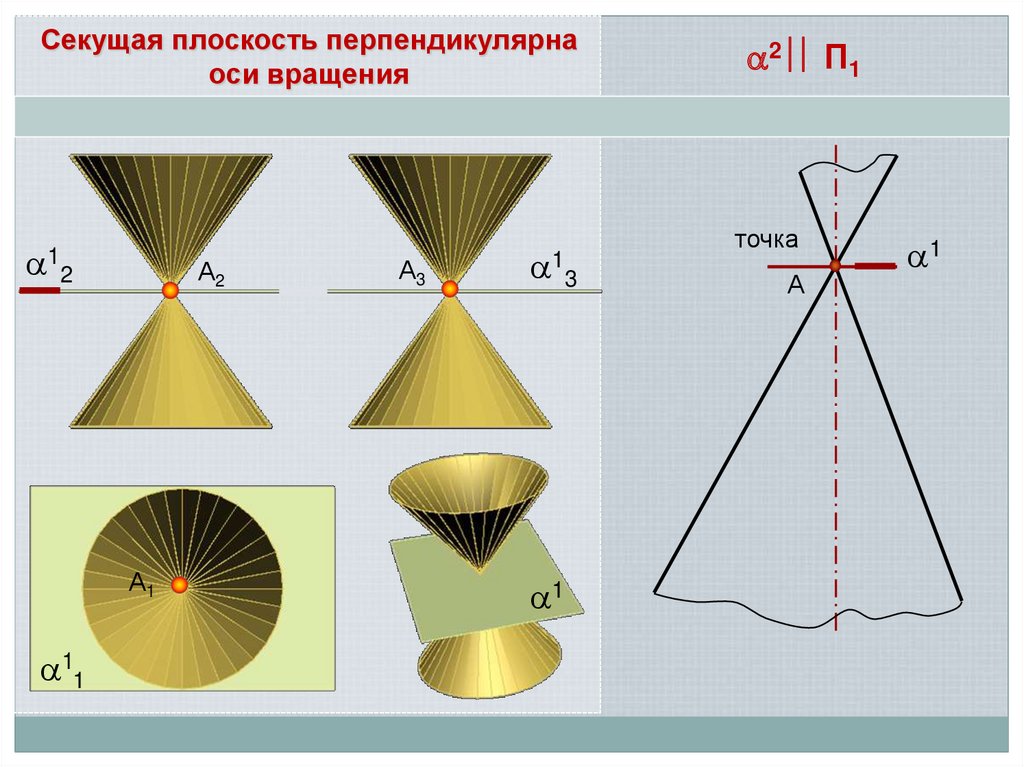
Секущая плоскость перпендикулярнаоси вращения
23
22
2
21
2 П1
15.
точкаокружность
1
2
16.
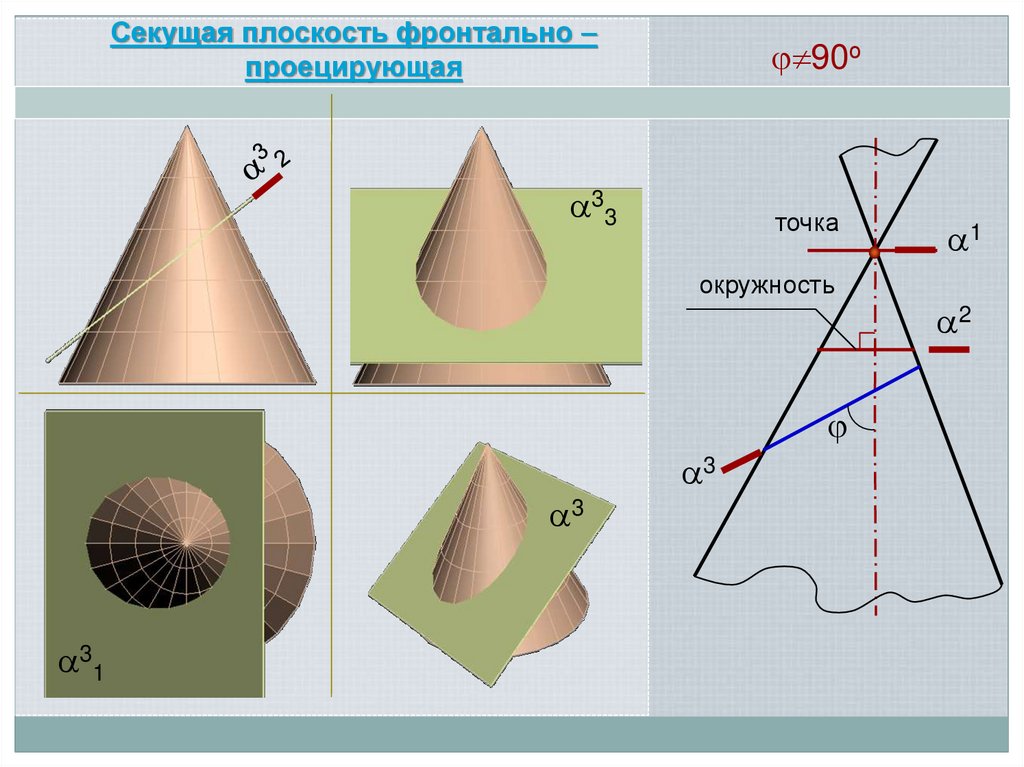
Секущая плоскость фронтально –проецирующая
90о
33
точка
окружность
3
3
31
1
2
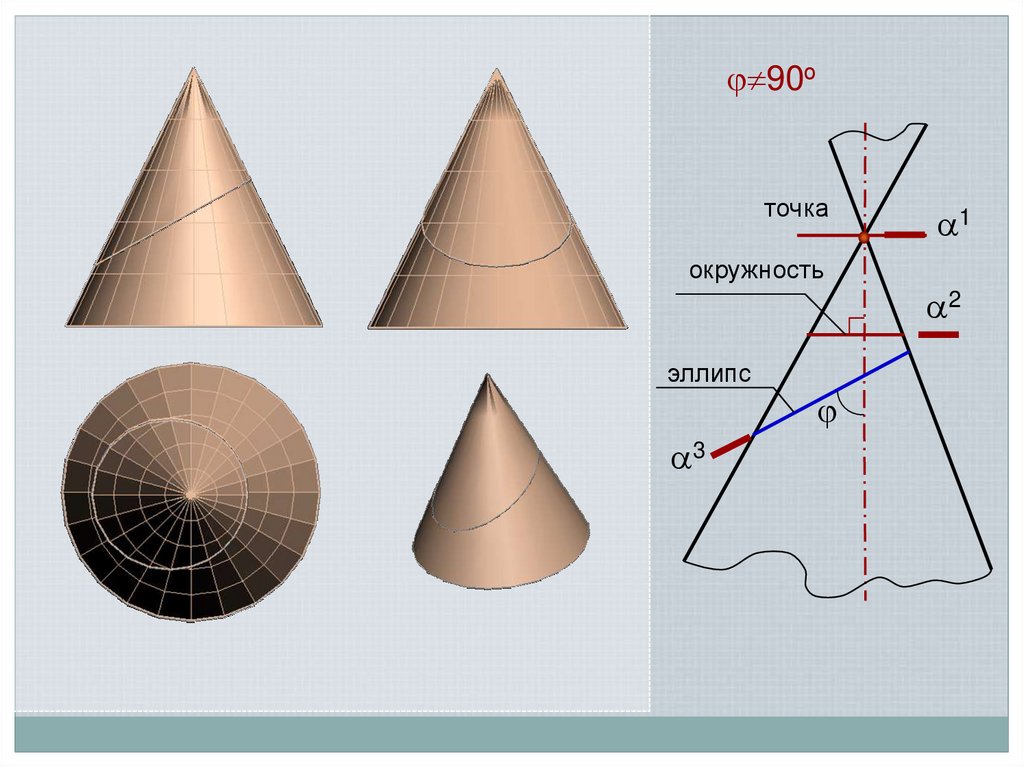
17.
90оточка
окружность
эллипс
3
1
2
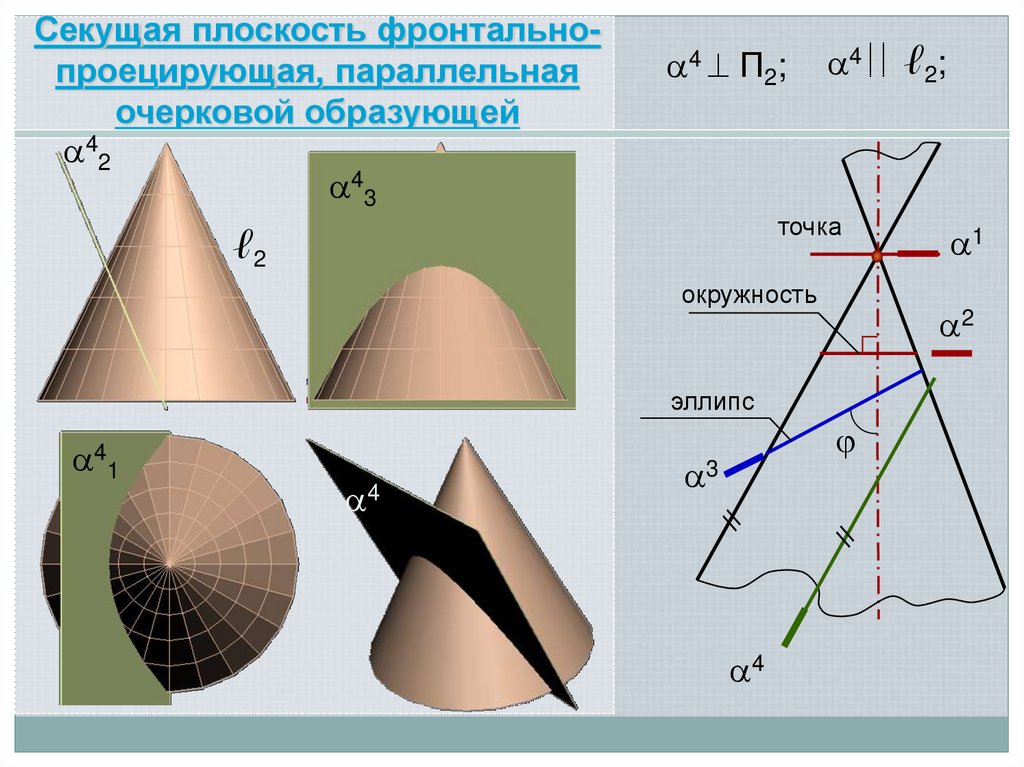
18.
Секущая плоскость фронтальнопроецирующая, параллельнаяочерковой образующей
42
43
4 П2;
4 ℓ2;
точка
ℓ2
окружность
2
эллипс
41
4
3
4
1
19.
точкаокружность
2
эллипс
3
парабола
4
1
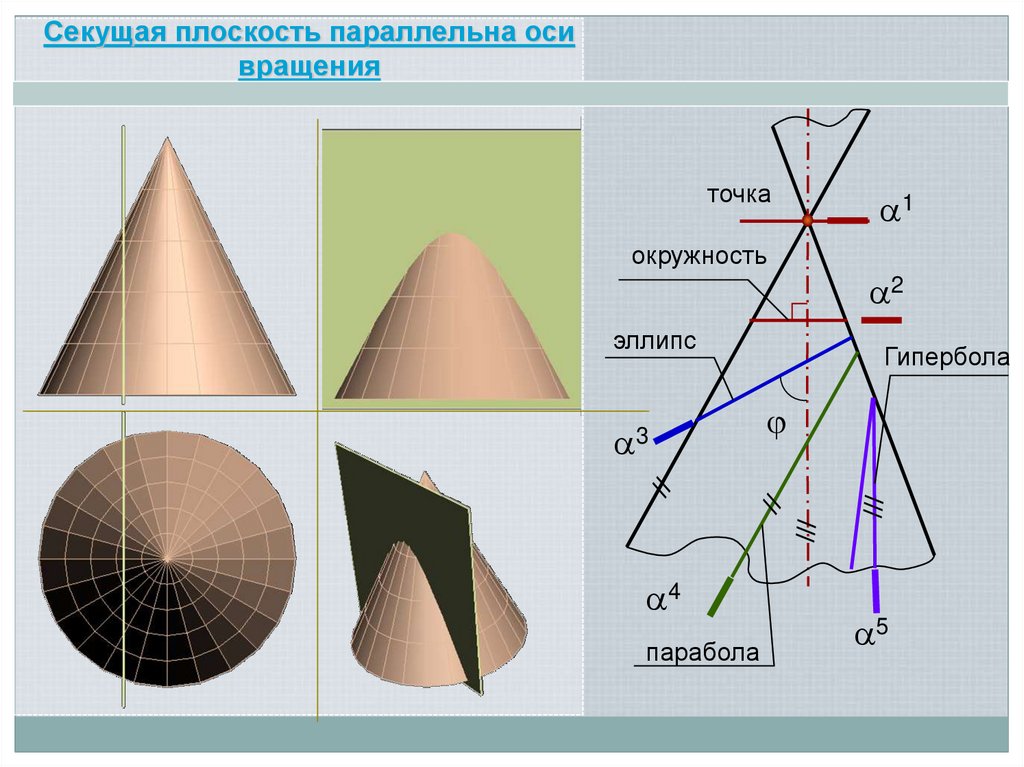
20.
Секущая плоскость параллельна осивращения
точка
окружность
эллипс
3
4
парабола
1
2
Гипербола
5
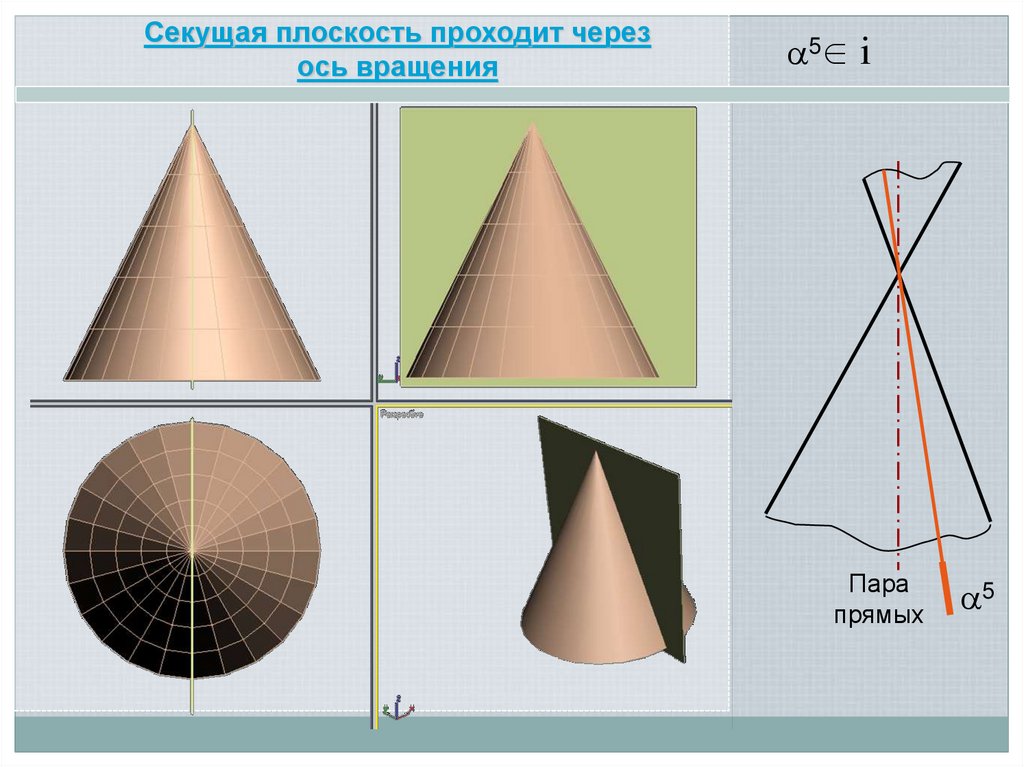
21.
Секущая плоскость проходит черезось вращения
5∈ i
Пара
прямых
5
22.
ЗадачаПостроить линию пересечения поверхности тора
фронтально проецирующей плоскостью
2
2
А2
121≡12
1
2
В21≡В2
2
В11
221≡22 R
211
111
А1
2гм
В1
21
11
23.
Пересечение поверхности общегоположения с плоскостью общего
положения
24.
Обе проекции искомой линиипересечения строятся в плоскостях П1 и
П2, с использованием метода секущих
плоскостей или способом замены
плоскостей проекций
25.
Алгоритм решения задач на пересечениеповерхности общего положения
с плоскостью общего положения
1. Поверхность и плоскость пересекают
вспомогательной плоскостью посредником .
2. Находят линию пересечения плоскостипосредника с поверхностью Ф: n = Ф .
3. Находят линию пересечения плоскостипосредника с заданной плоскостью : MN = .
4.Отмечают точки, в которых эти линии
пересекутся: 1,2 – MN n Точки 1 и 2, являясь
общими для данных поверхности и плоскости
будут точками искомой линии пересечения.
5. Для построения линии пересечения
необходимо найти еще ряд точек (3,4,5…),
используя плоскости-посредники
26.
S3S1
2
3
ВТ2
( )
очерк
ВТ3
НТ3
НТ2
1
S
ВТ1
S2
НТ1
Главный
меридиан П3
1
27.
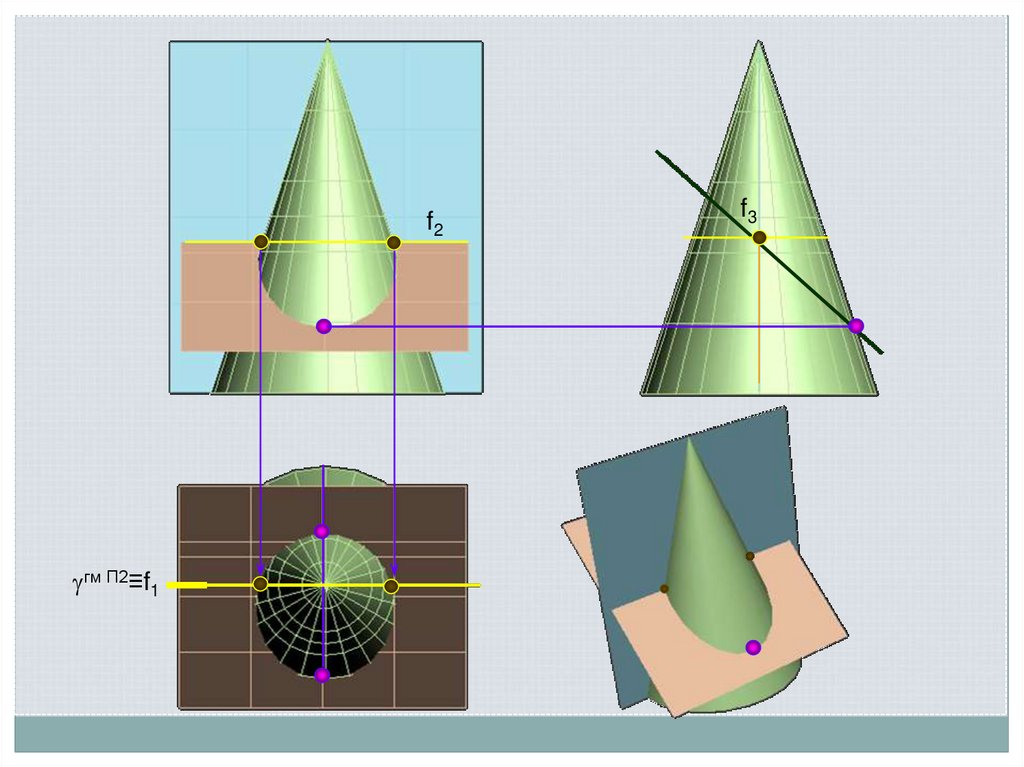
f2гм П2≡f1
f3
28.
29.
12гм
12
22
13≡23
11
21
2
1
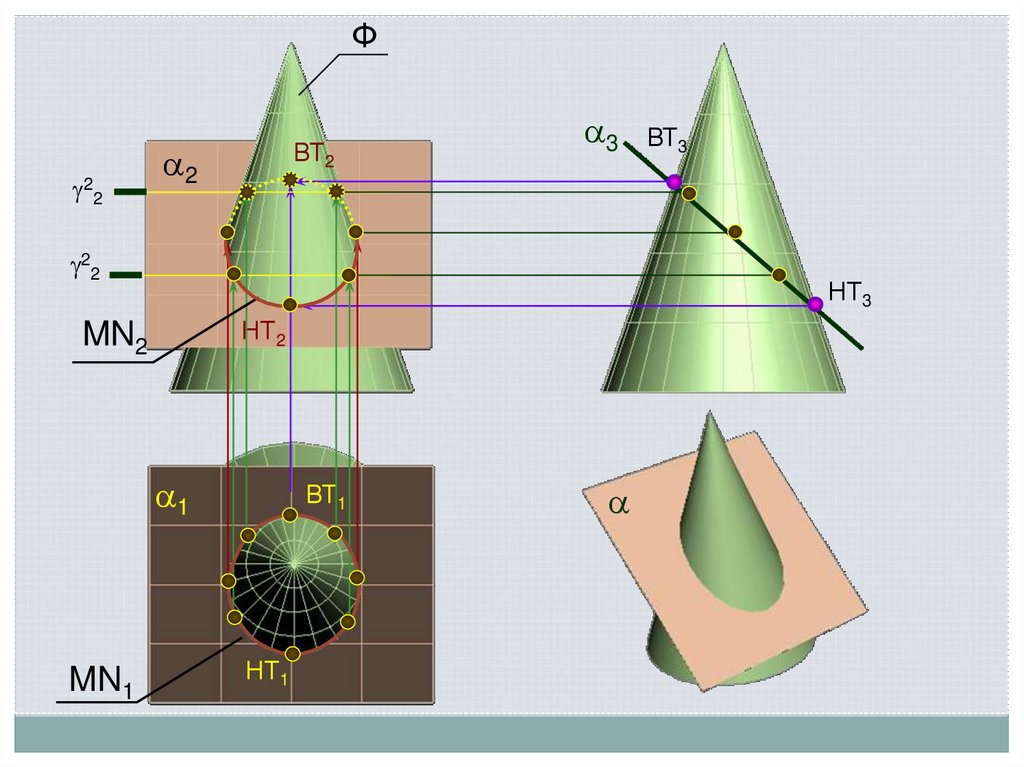
30.
Ф2
ВТ2
2
3
ВТ3
2
2 2
НТ3
НТ2
MN2
1
MN1
ВТ1
НТ1
31.
А2Задача
S2
ί2
f2
C2B2(h2)≡ox
G2 (ВТ )
2
212
z 22
12
Х1,2
П2
П1
гм П2≡f1
С2
//
А1
112
Q2
НТ2 h2
В1
211
G1
гм
111
Q1
ВТ1
//
ί1
21
S1
14≡114
ВТ4
24≡214
h1
f1
НТ1
11
А4
В2
С1
НТ4 С ≡B
4
4
32.
Пересечение прямой с поверхностьюАлгоритм
1. Через прямую АВ проводят
вспомогательную плоскость – посредник
2. Находят линию пересечения поверхности
с плоскостью - k
3. Отмечают точки пересечения прямой АВ
с линией k, точки 1 и 2
Количество точек пересечения прямой
с поверхностью определяет порядок последней
33.
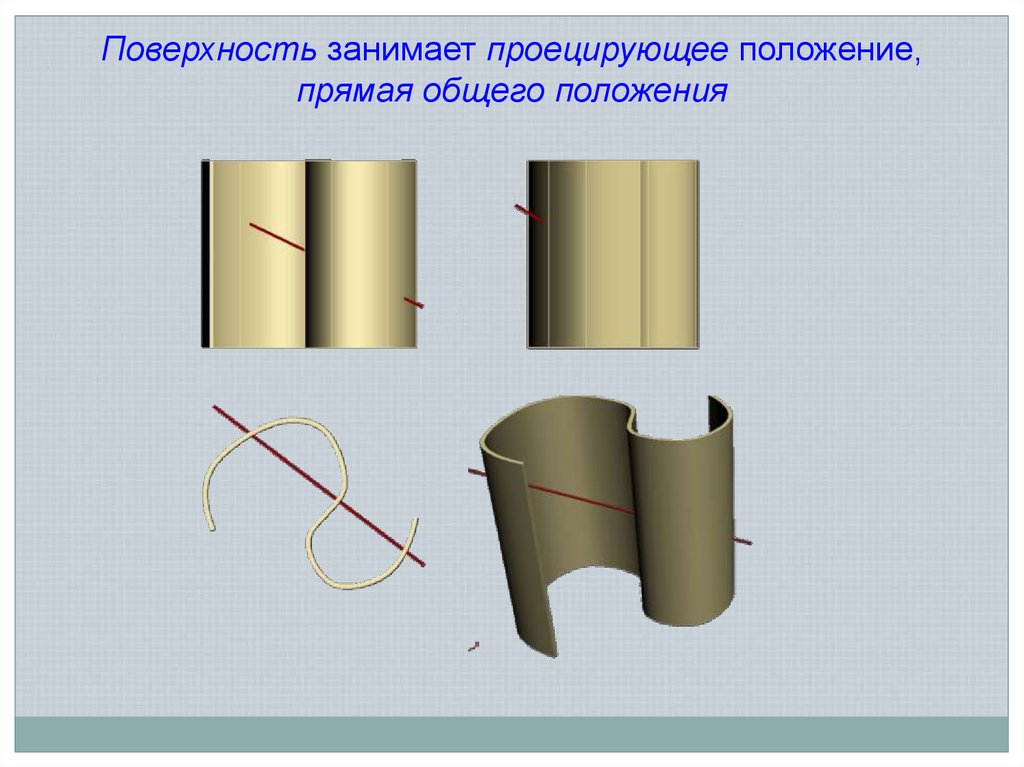
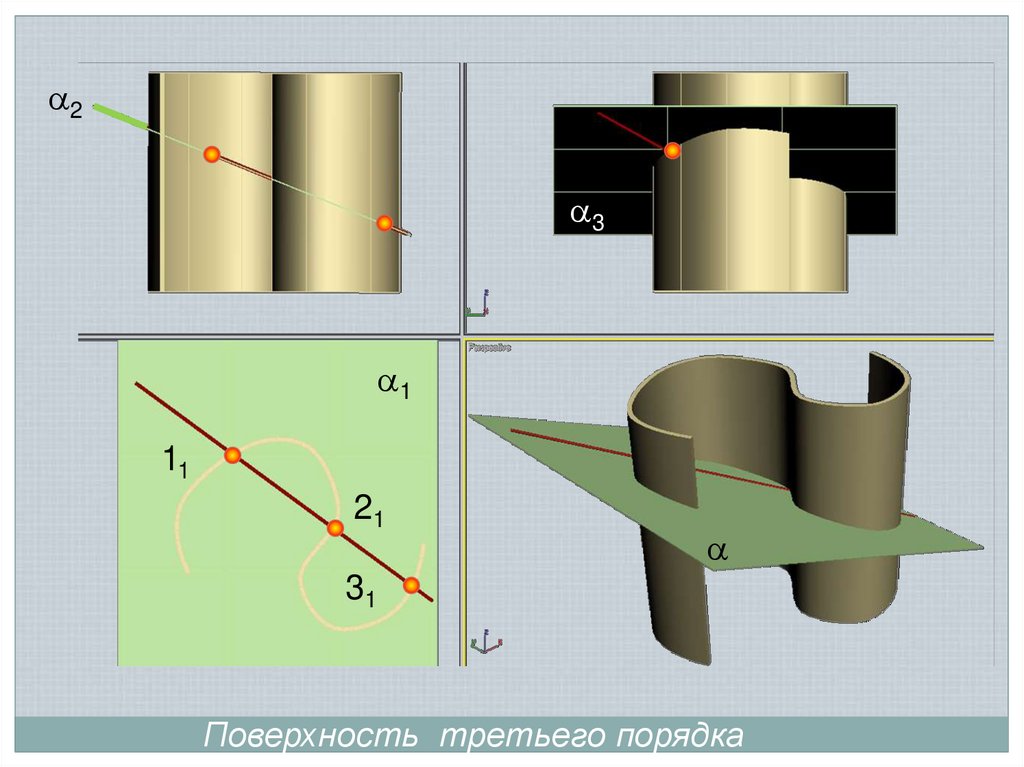
Поверхность занимает проецирующее положение,прямая общего положения
34.
23
1
11
21
31
Поверхность третьего порядка
35.
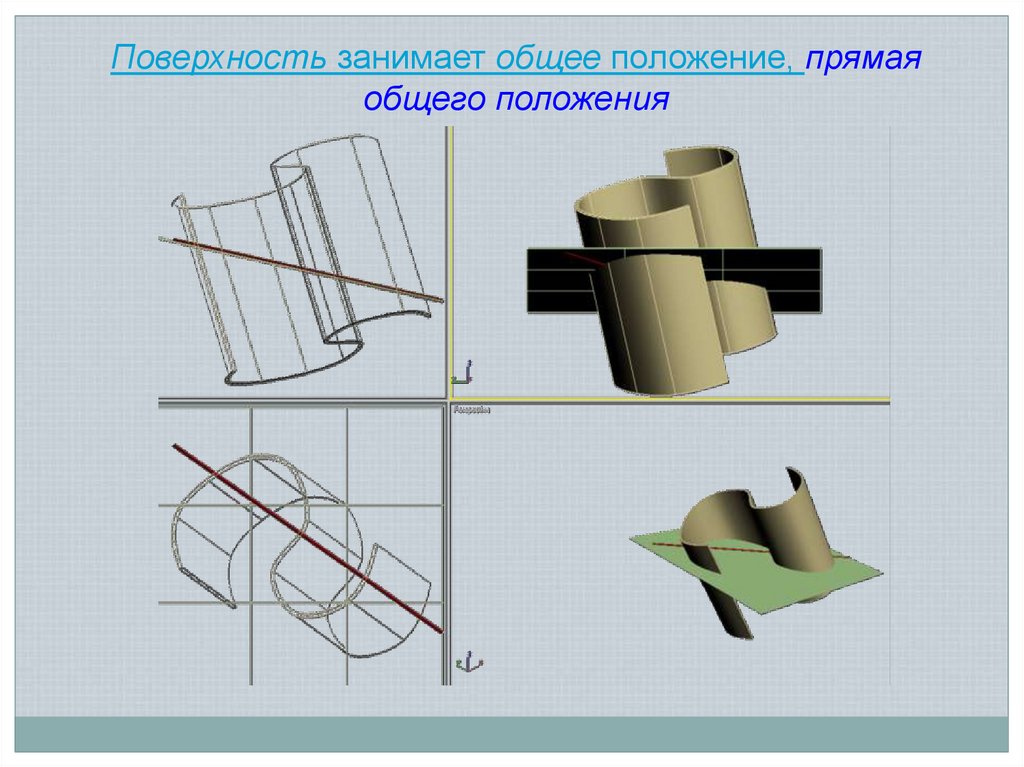
Поверхность занимает общее положение, прямаяобщего положения
36.
23
1
11
21
31
31
Поверхность третьего порядка






















 mathematics
mathematics








