Similar presentations:
Умножения вектора на число
1.
2. Цель урока:
• Рассмотреть основные свойстваумножения вектора на число
• Сформировать навыки решения задач
на применение свойств умножения
вектора на число
3.
хJO = – 1
4 CK
СК = -4х JO
х
XD =– 3
4 CK
A
B
C
D
N
M
R
E
S
F
Q
I
V
T
Y
U
NN = 0х XD
ХТ = х XD
х не существует
XT =1х XT
O
P
X
G
TX = -х1 XT
H
J
K
L
Z
4.
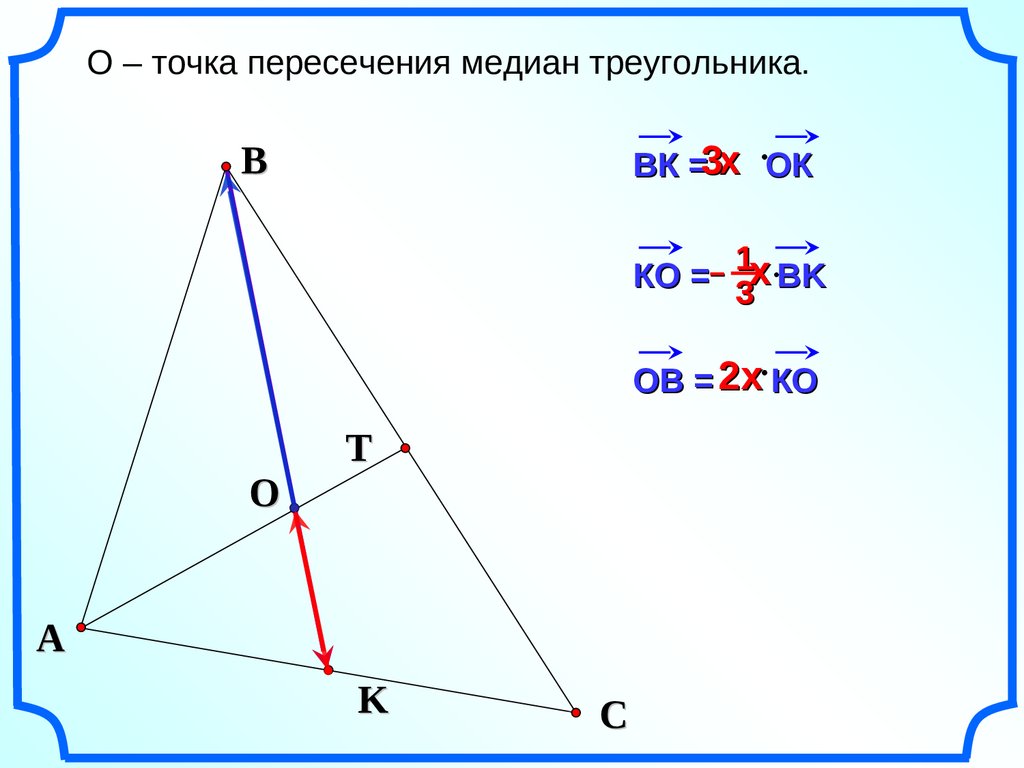
О – точка пересечения медиан треугольника.ВК =3х ОК
B
х
КO =– 1
3 ВK
ОВ = 2х КО
O
T
A
K
C
5.
ABCD – трапеция.В
С
8
BC = – х
0,8
DA
х
DA = – 10
8 BC
А
10
D
6.
Умножение вектора на число обладает следующимиосновными свойствами.
Для любых
равенства:
a ,b
и любых чисел
1
(kl)a = k (l a)
2
(k+l)a = ka + la
k ,l
справедливы
Сочетательный закон
Первый распределительный закон
3
k (a + b) = ka + kb
Второй распределительный закон
7.
№ 781 Пусть х = m + n, y = m – nВыразите через m и n
векторы
2х – 2у 2(m n ) 2(m n ) 2m 2n 2m 2n 4n
1
1
1
2(m n ) (m n ) 2m 2n m n
2
2
2
1
1
2 m 1 n
2
2
1
1
1
–х – 13 у (m n ) (m n ) m n m n
3
3
3
1
2
1 m n
3
3
2х + 12 у
8.
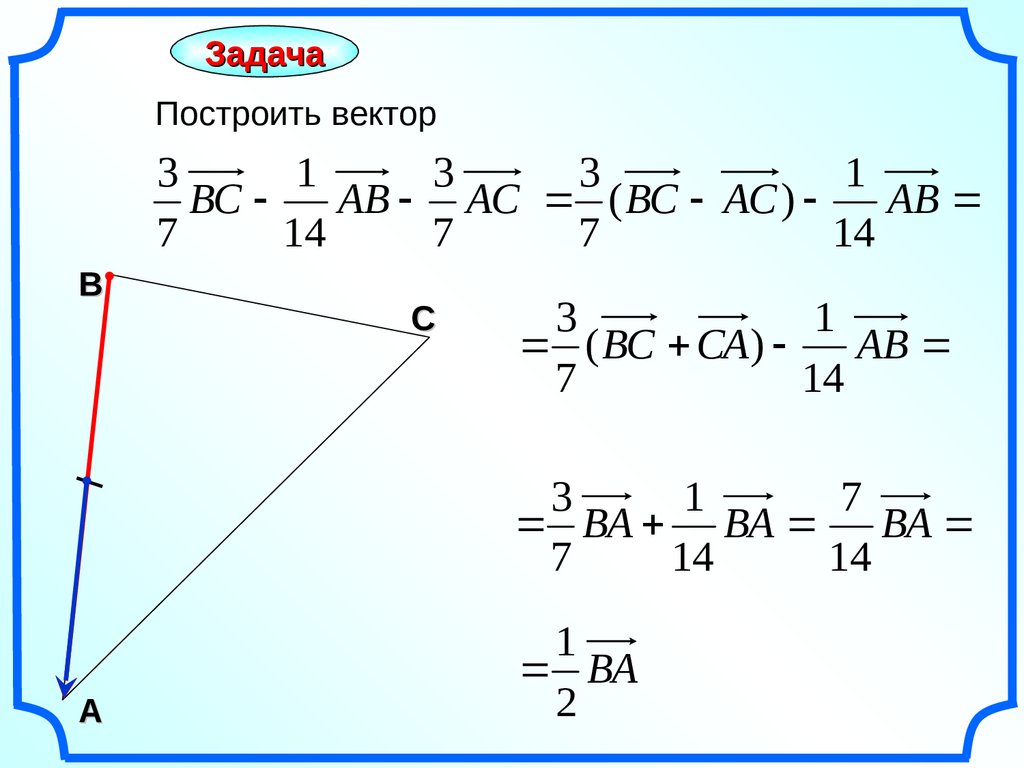
ЗадачаПостроить вектор
3
1
3
3
1
ВС
АВ АС ( ВС АС )
АВ
7
14
7
7
14
В
С
3
1
( ВС СА)
АВ
7
14
3
1
7
ВА ВА ВА
7
14
14
А
1
ВА
2
9.
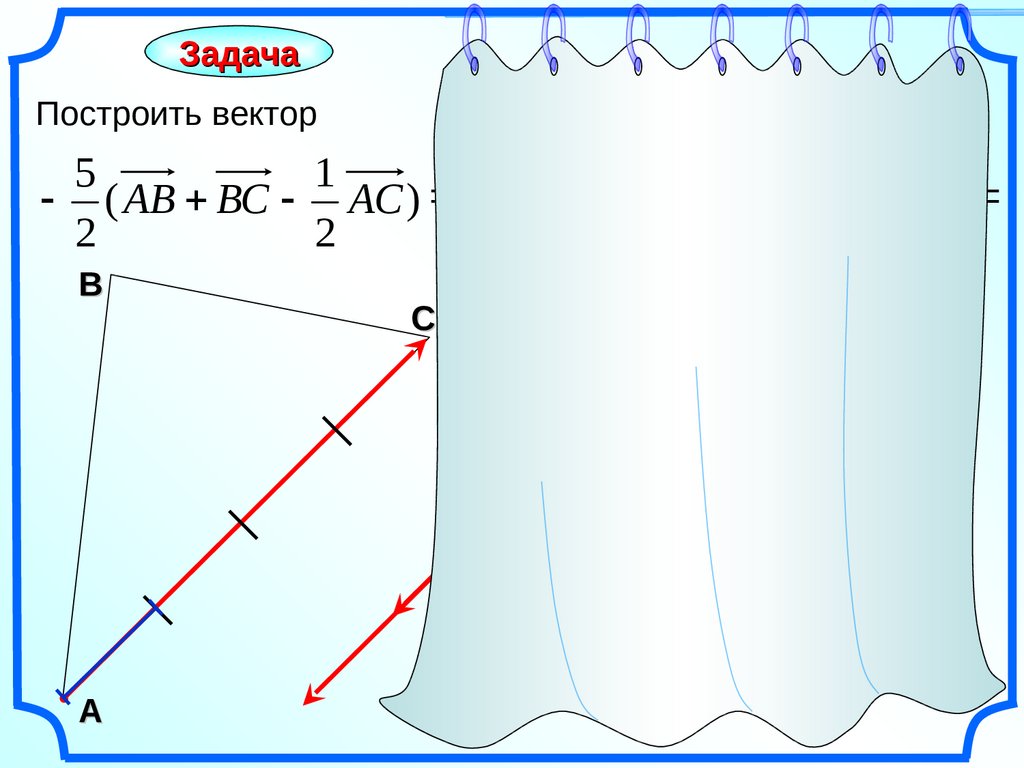
ЗадачаПостроить вектор
5
1
5 1
5
1
( АВ ВС АС ) ( АС АС ) АС
2
2
2 2
2
2
В
5
АС
С
4
А
10.
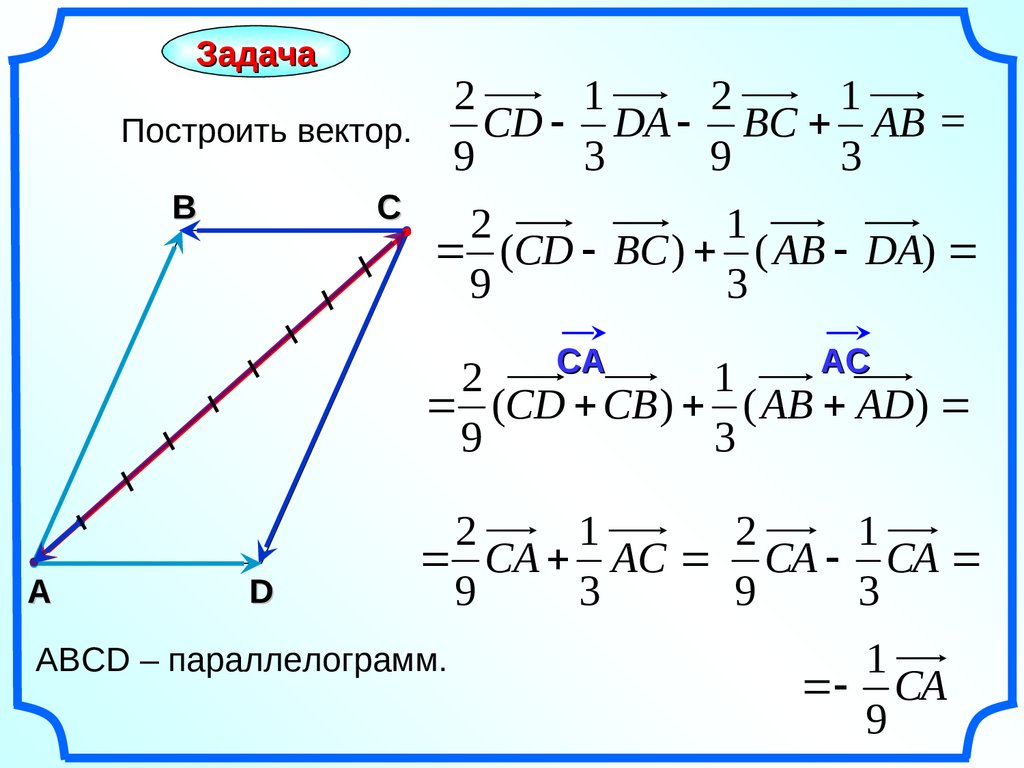
Задача2
1
2
1
СD DA BС AB =
9
3
9
3
Построить вектор.
В
С
2
1
(СD BС ) ( АВ DA)
9
3
CA
AC
2
1
(СD СB ) ( АВ AD)
9
3
А
D
2
1
2
1
CA AC СА СА
9
3
9
3
АВСD – параллелограмм.
1
СА
9
11.
Построить вектор.Задача
2
1
2
АВ
СA DA
5
10
5
2
1
( АВ DA)
CА
5
10
В
С
AC
2
1
( АВ AD )
CА
5
10
2
1
5
AС AC АС
5
10
10
А
D
АВСD – параллелограмм.
1
АС
2
12.
ЗадачаB
C
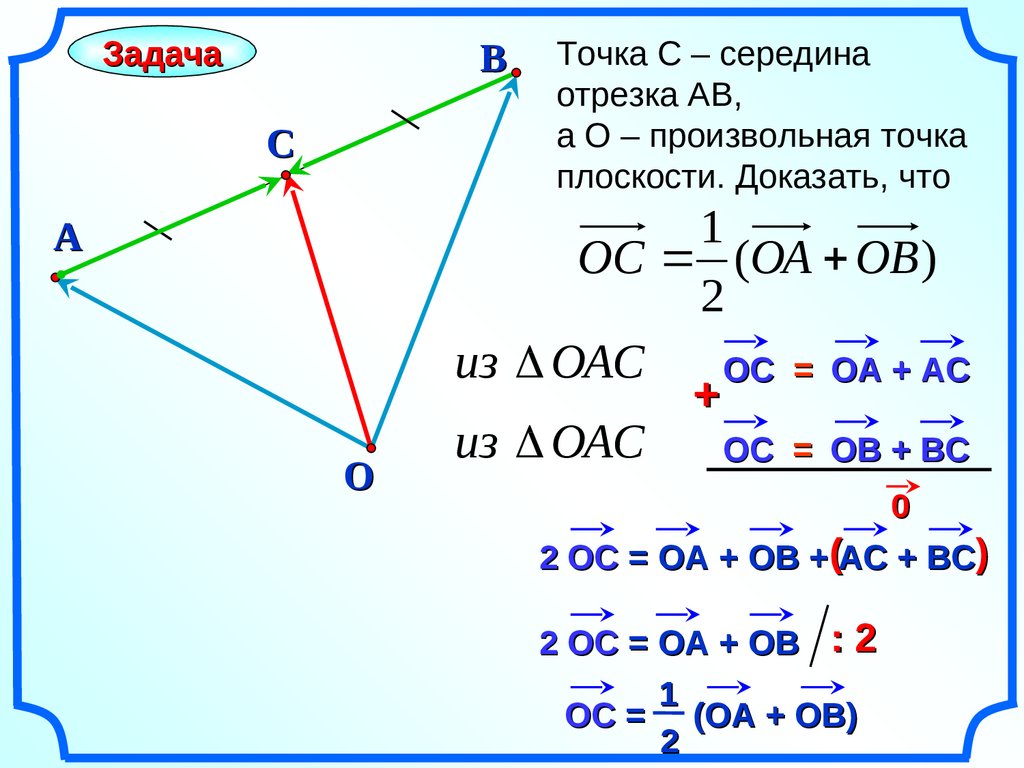
Точка С – середина
отрезка АВ,
а О – произвольная точка
плоскости. Доказать, что
1
ОС (ОА ОВ )
2
из ОАС
OС = OА + АС
A
O
из ОАС
+
OС = OВ + ВС
0
2 OС = ОА + ОВ +(АС + ВС)
2 OС = ОА + ОВ : 2
1
OС = (ОА + ОВ)
2
13.
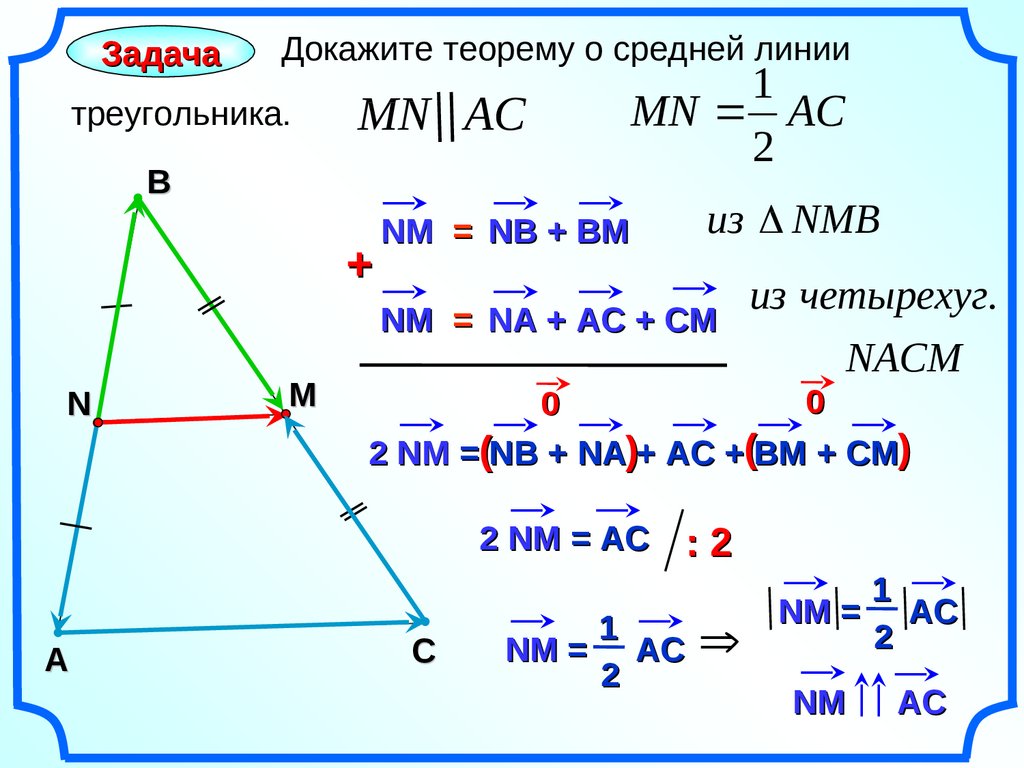
ЗадачаДокажите теорему о средней линии
треугольника.
MN AC
В
+
N
M
1
MN AC
2
из четырехуг.
NM = NA + AС + CM
NACM
0
0
2 NM =(NB + NA)+ АС +(ВM + CM)
2 NM = AC
A
из NMB
NM = NB + BM
С
:2
1
NM = AC
2
1
NM = AC
2
NM
AC
14.
ТеоремаВ
Средняя линия трапеции параллельна
основаниям и равна их полусумме.
MN AD BC
С
+
NM = NB + BС + СМ
NM = NA + AD + DM
Правило
многоугольника
N
1
MN ( AD BC )
2
0
0
M
2NM =(NB + NA)+ BС + AD + (CM +DM )
2NM = ВC + AD
A
D
NM
BC
1
NM = (BC+AD)
2
AD;
:2
1
NM = BC+AD
2
15.
АВСD – ромб. Е ВС, ВЕ : ЕС = 3 : 1,Задача
К – середина DC, АВ =
векторы
a
и
b
b . Выразите через
3
AE AB BE AB BC a b
4
из АВЕ
a
1
AK AD DK AD DС
2
из АDK
E
А
С
K
D
AD =
векторы:
В
b
a,
1
b a
2
1
KE KA AE (b a ) ( a b)
2
из АEK
1
a
2









 mathematics
mathematics








