dc14679d221643bd8fede140c6c67731

1.

2.

Естественно
считать,
что одно
вектор
2v получается
Если мы чем
изобразим
первого
автомобиля
Прежде,
ввести скорость
еще
действие
– умножение
умножением
v на число
2, а вектор
-2v получается
вектором
v, число,
товектора
естественно
изобразить
скорость
второго
вектора на
обратимся
к примеру.
Представим
себе,
умножением
вектора vдвижется
число прямолинейно
-2.
Этот пример
автомобиля
вектором,
унакоторого
направление
что один автомобиль
стакое же,
показывает
каким
образом
вести виумножение
как
у вектора
v, а длина
в 2 следует
разадвижется
больше,
обозначить
этот
постоянной
скоростью,
второй
том
же
вектора
наСкорость
число
и что
при умножении
получается
вектор.
вектор
2v.
третьего
автомобиля
изобразиться
направлении
со скоростью,
вдвое
большей,
а третий
вектором,
противоположным
вектору т.е.
2v, в
т.е. вектором -2v.
автомобиль
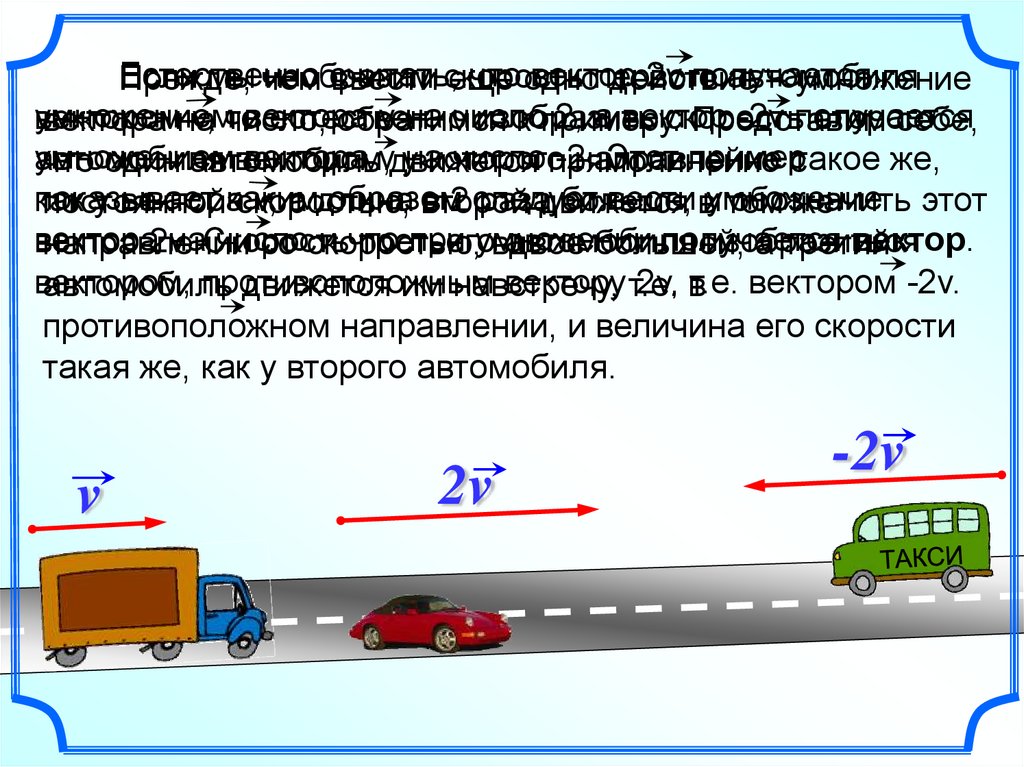
движется им навстречу,
противоположном направлении, и величина его скорости
такая же, как у второго автомобиля.
v
2v
-2v

3.

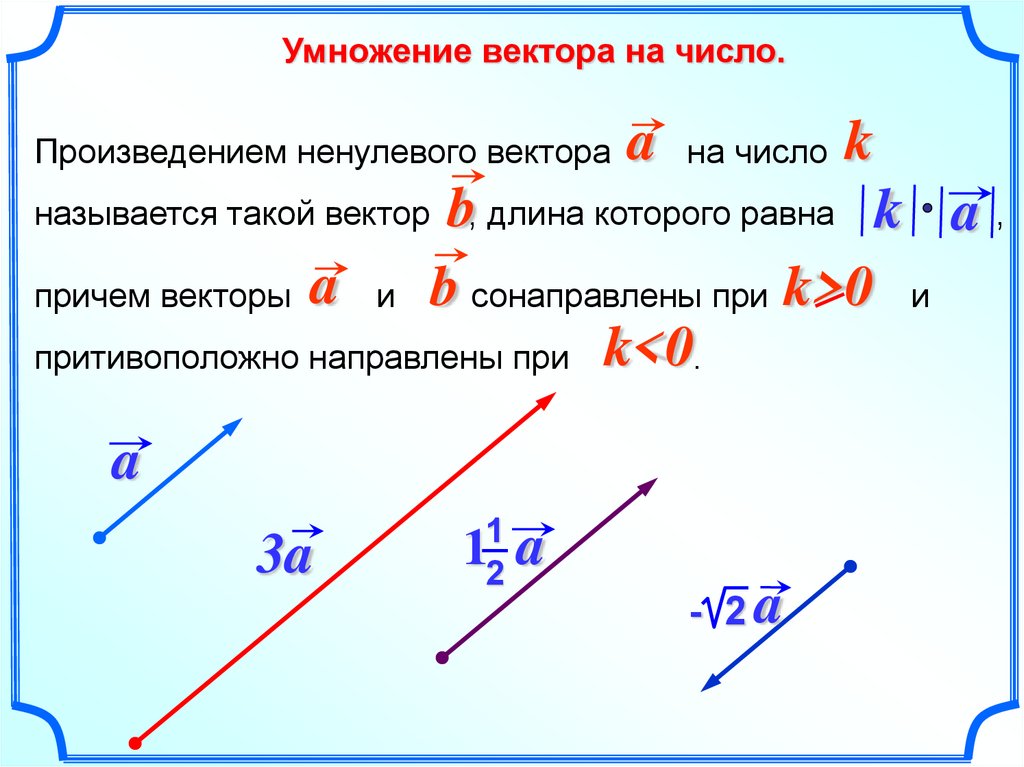
Умножение вектора на число.
Произведением ненулевого вектора
a на число k
b, длина которого равна k a ,
причем векторы a и b сонаправлены при k>0 и
притивоположно направлены при k<0.
называется такой вектор
a
3a
1
12
a
- 2a

4.

Умножение вектора на число.
b
2b
a
1
a
2
2b b
2b = 2 b
1
a
2
a
1
a
=
2
1
2
a

5.

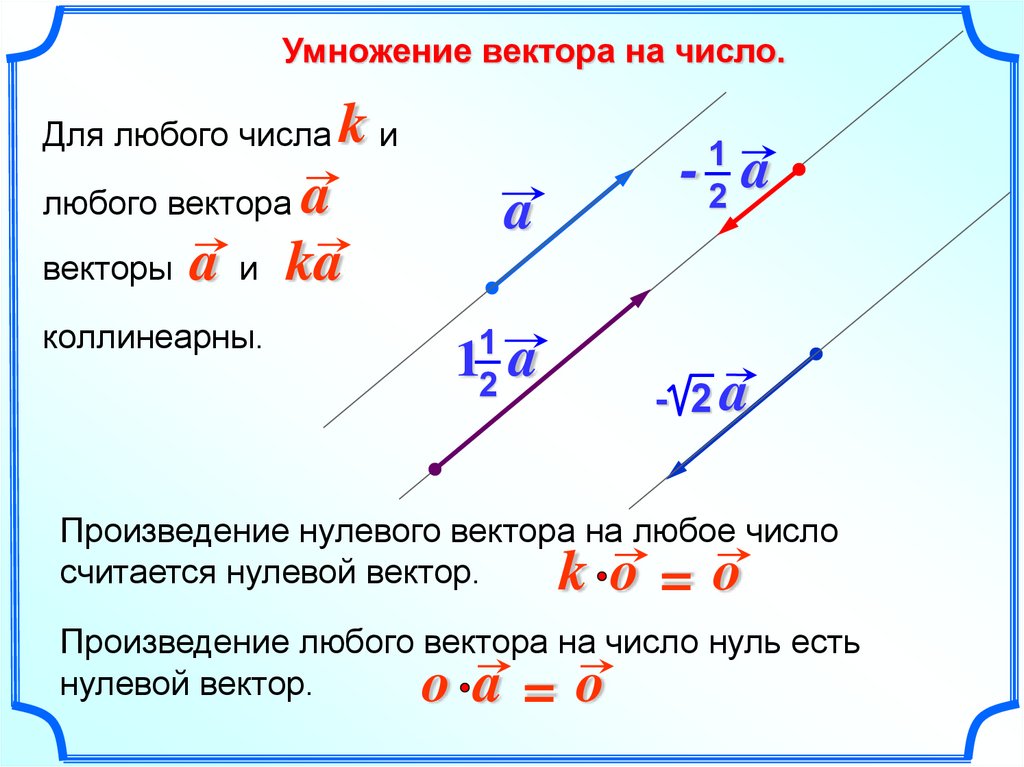
Умножение вектора на число.
Для любого числа
kи
a
векторы a и ka
любого вектора
коллинеарны.
1
2
- a
a
1
12
a
- 2a
Произведение нулевого вектора на любое число
считается нулевой вектор.
k o=o
Произведение любого вектора на число нуль есть
нулевой вектор.
o a=o

6.

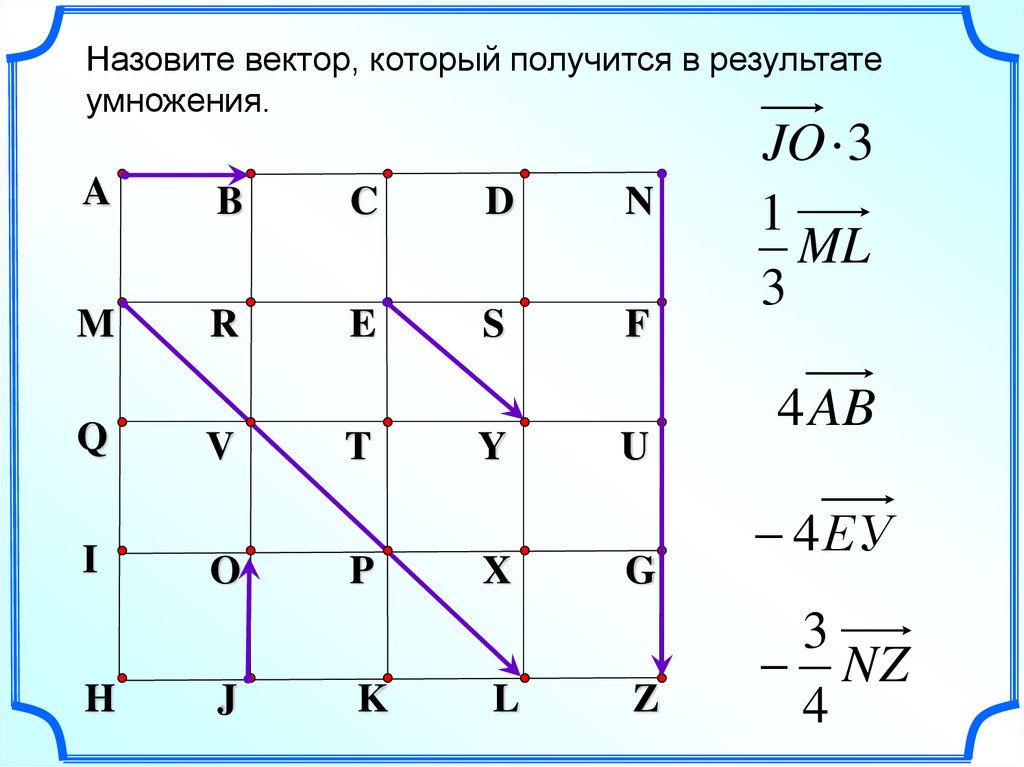
Назовите вектор, который получится в результате
умножения.
A
B
C
D
N
M
R
E
S
F
Q
I
H
V
O
J
T
P
K
Y
X
L
U
G
Z
JO 3
1
ML
3
4 AB
4 ЕУ
3
NZ
4

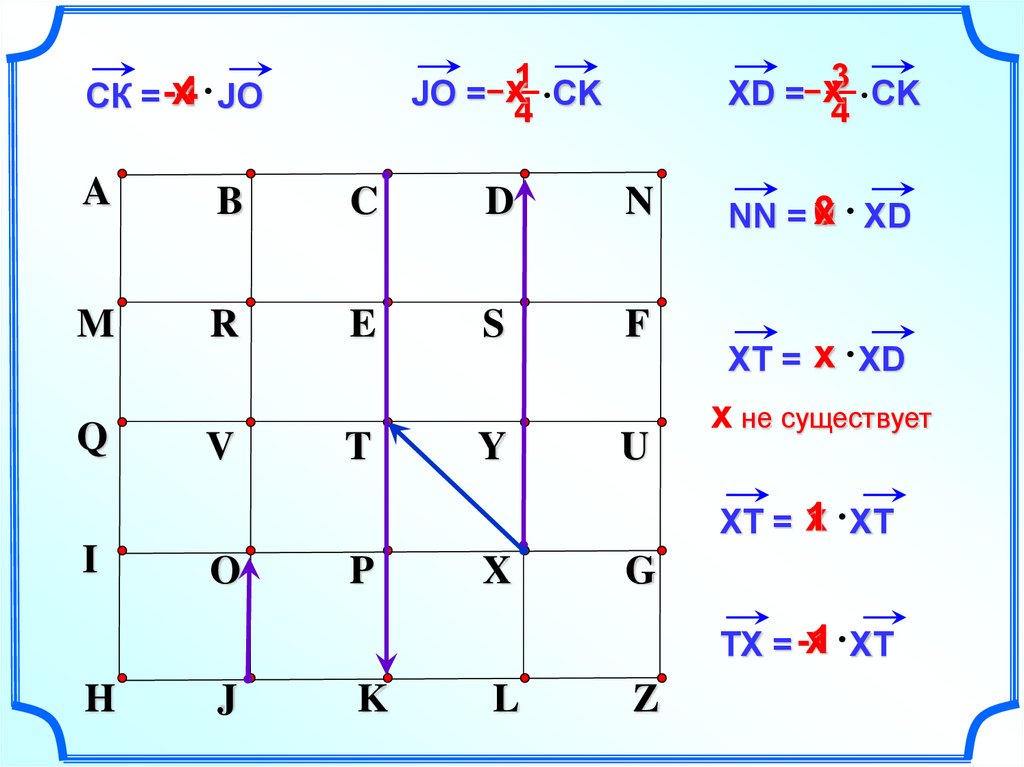
7.

х JO
СК = -4
JO = – х1
4 CK
XD =– х3
4 CK
A
B
C
D
N
0 XD
NN = х
M
R
E
S
F
ХТ = х XD
Q
V
T
Y
U
х не существует
х XT
XT = 1
I
O
P
X
G
х XT
TX = -1
H
J
K
L
Z

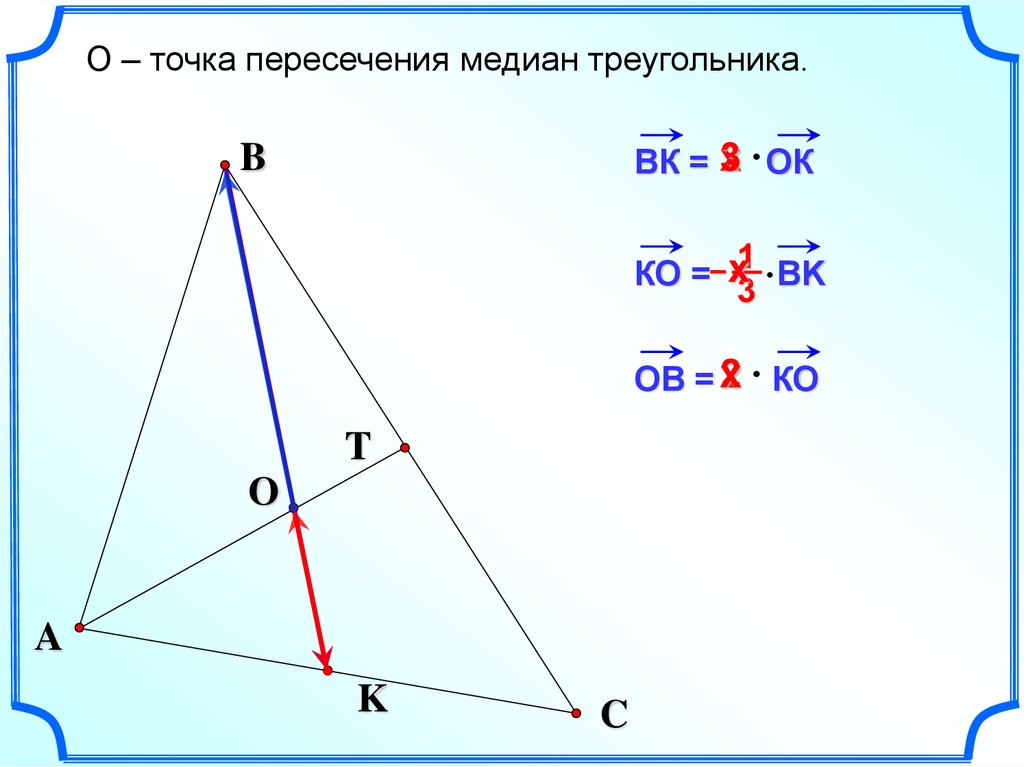
8.

О – точка пересечения медиан треугольника.
3 ОК
ВК = х
B
КO =– х1
3 ВK
2 КО
ОВ = х
T
O
A
K
C

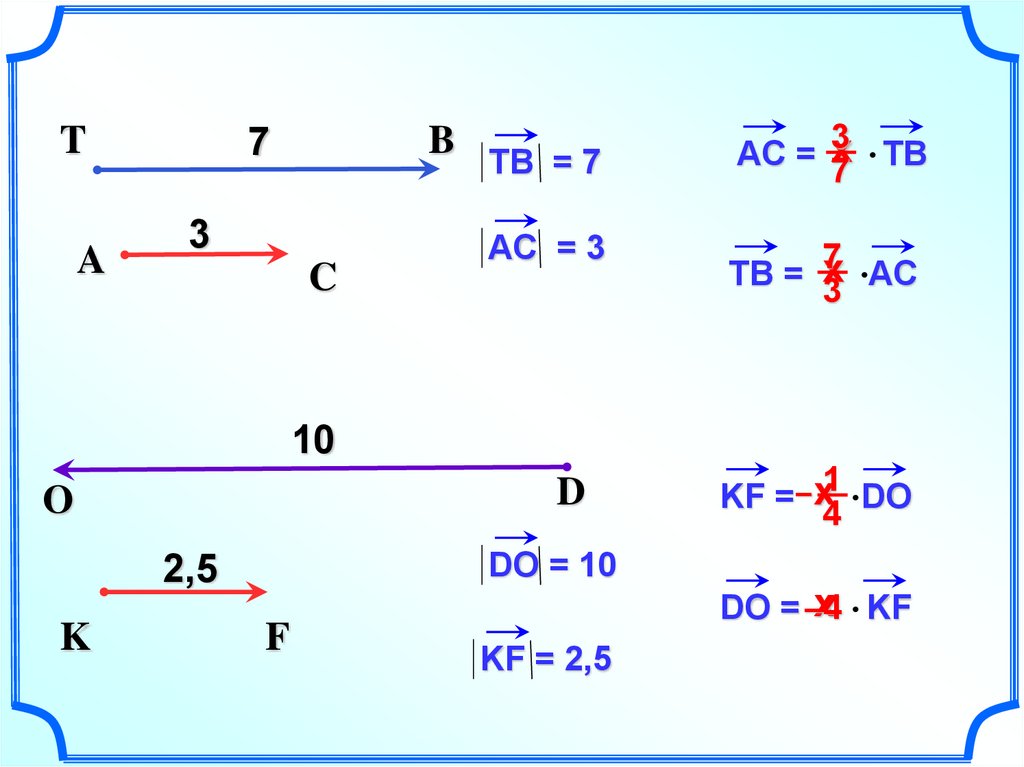
9.

T
A
B
7
3
C
TВ = 7
х TВ
AC = 3
7
AC = 3
х AC
TB = 7
3
D
KF = – х1 DO
4
10
O
DO = 10
2,5
K
F
KF = 2,5
х KF
DO = –4

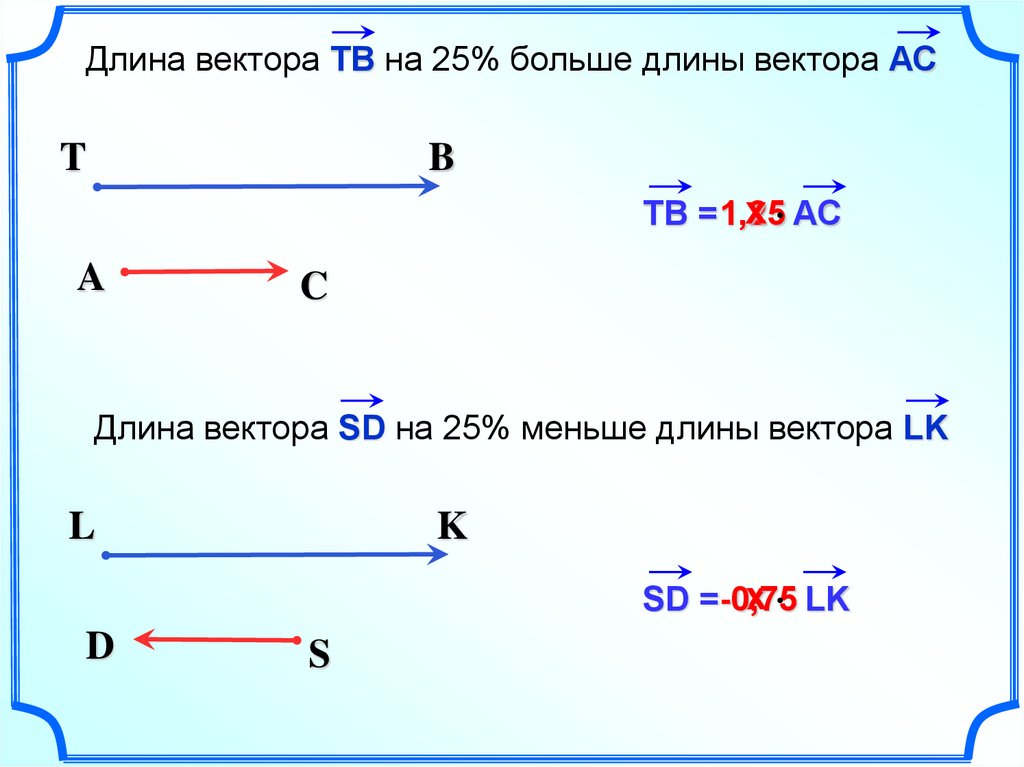
10.

Длина вектора TB на 25% больше длины вектора АС
T
B
х АС
ТВ = 1,25
A
C
Длина вектора SD на 25% меньше длины вектора LK
L
K
х LK
SD =-0,75
D
S

11.

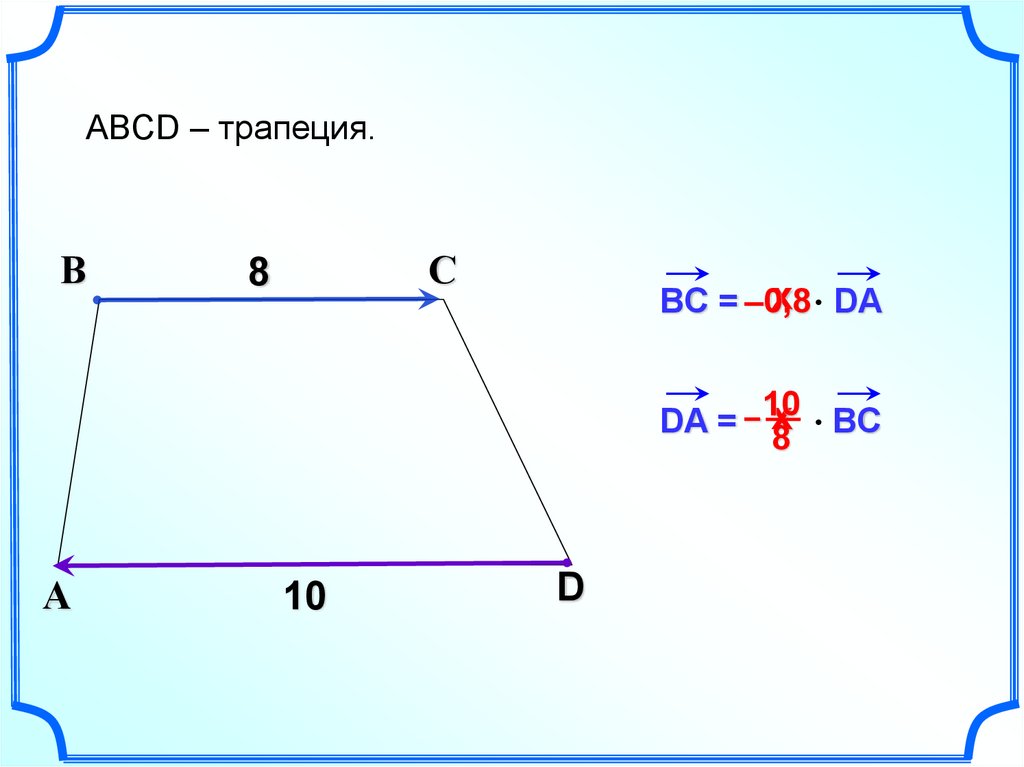
ABCD – трапеция.
В
С
8
х DA
BC = –0,8
х BC
DA = – 10
8
А
10
D

12.

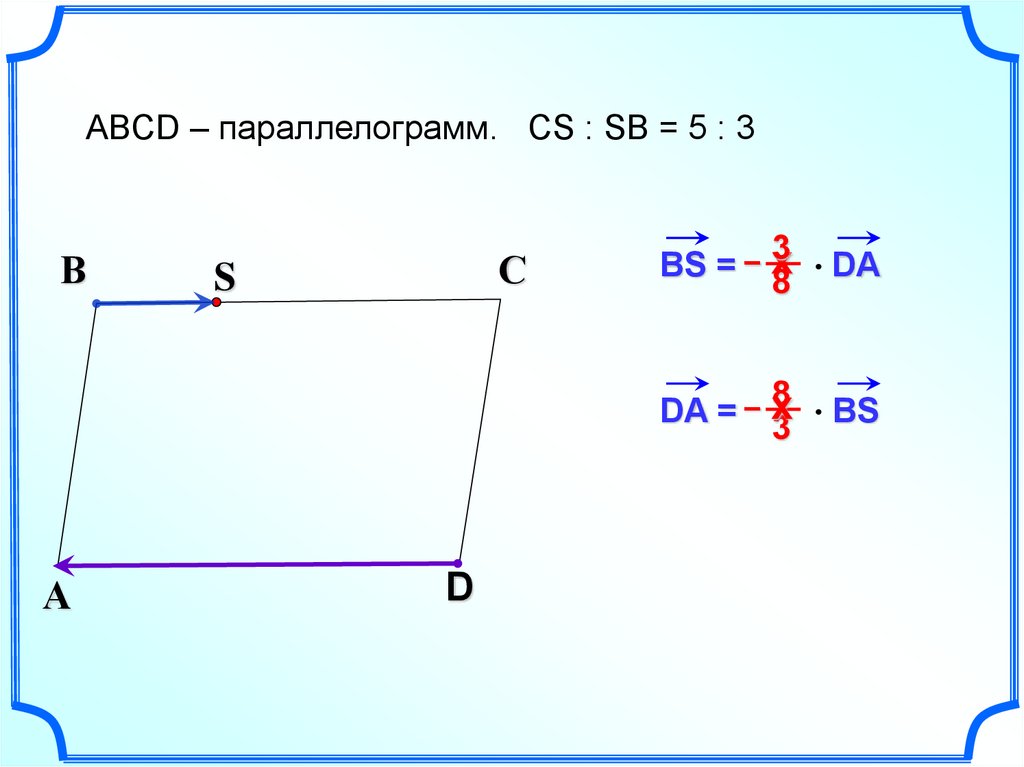
ABCD – параллелограмм. CS : SB = 5 : 3
В
С
S
3 DA
BS = – х
8
8 BS
DA = – х
3
А
D

13.

Умножение вектора на число обладает следующими
основными свойствами.
Для любых
равенства:
a , b и любых чисел k, l справедливы
1
(kl)a = k (l a)
2
(k+l)a = ka + la
Сочетательный закон
Первый распределительный закон
3
k (a + b) = ka + kb
Второй распределительный закон

14.

Рисунок иллюстрирует сочетательный закон.
Представлен случай, когда
k = 2, l = 3.
1
Сочетательный закон
(kl)a = k (l a)
a
a
a
A
O
OВ = 2OA = 2(3
a a
B
a)
a a a a
B
O
OВ = 6
a = (2 3) a

15.

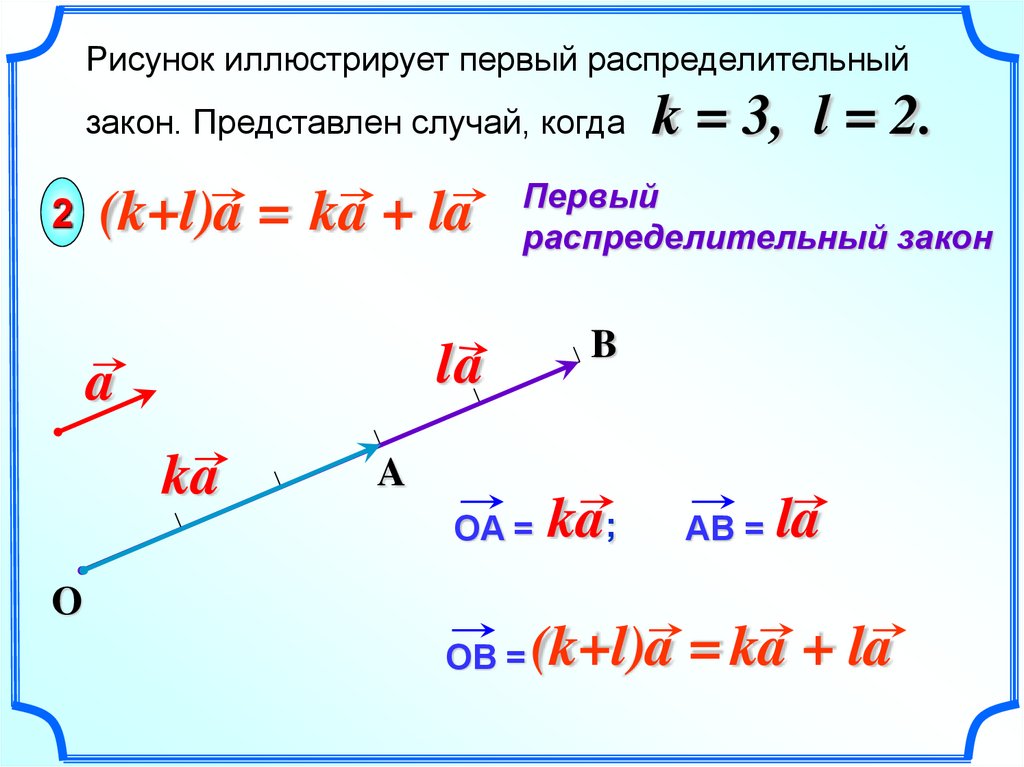
Рисунок иллюстрирует первый распределительный
закон. Представлен случай, когда
2 (k+l)a = ka + la
Первый
распределительный закон
B
la
a
ka
k = 3, l = 2.
A
OA =
ka;
AB =
la
O
OB =
(k+l)a = ka + la

16.

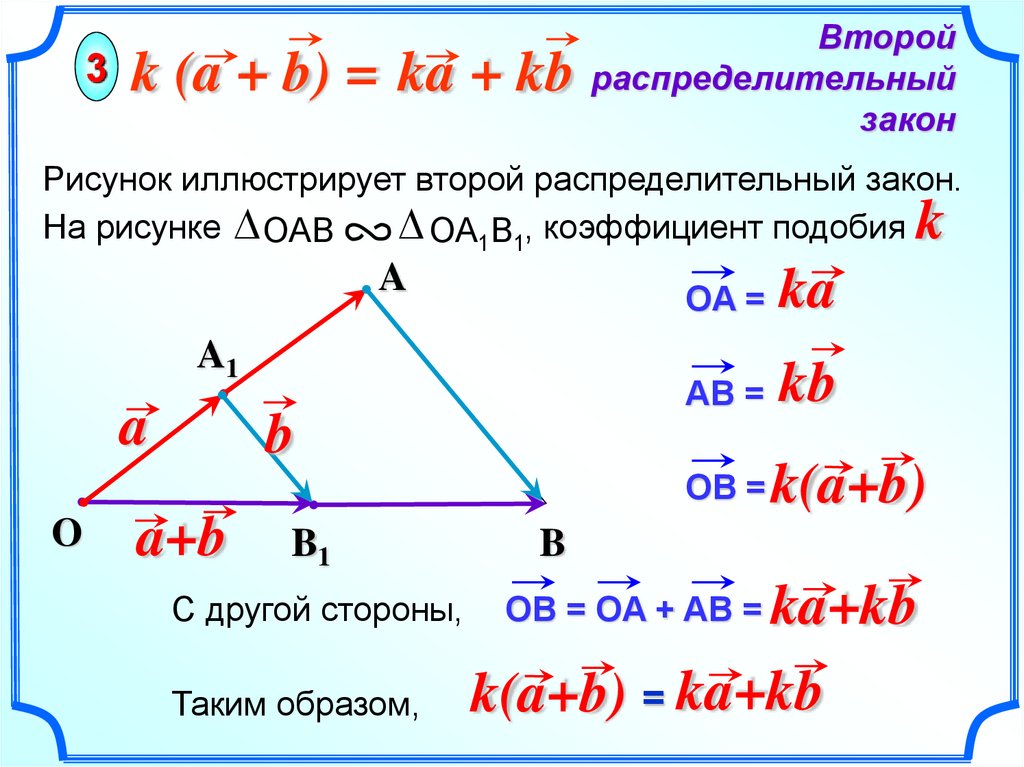
3 k (a + b) = ka + kb
Второй
распределительный
закон
Рисунок иллюстрирует второй распределительный закон.
ОА1В1, коэффициент подобия
На рисунке ОАВ
k
A
OA =
ka
AB =
kb
OB =
k(a+b)
С другой стороны,
OB = OA + AB =
ka+kb
Таким образом,
k(a+b) = ka+kb
A1
a
O
b
a+b
B1
B

17.

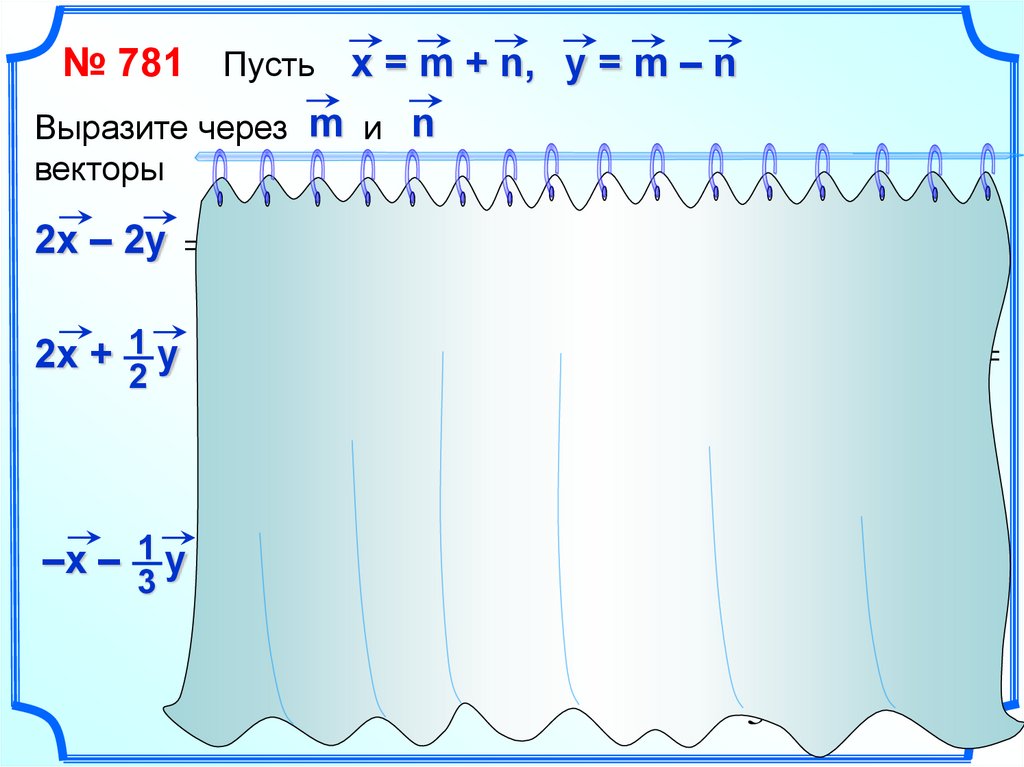
№ 781 Пусть х = m + n, y = m – n
Выразите через m и n
векторы
2х – 2у 2(m n ) 2(m n ) 2m 2n 2m 2n 4n
1
1
1
2( m n ) ( m n ) 2 m 2 n m n
2
2
2
1
1
2 m 1 n
2
2
1
1
1
–х – 1 у (m n ) (m n ) m n m n
3
3
3
3
1
2
1 m n
3
3
2х + 1 у
2

18.

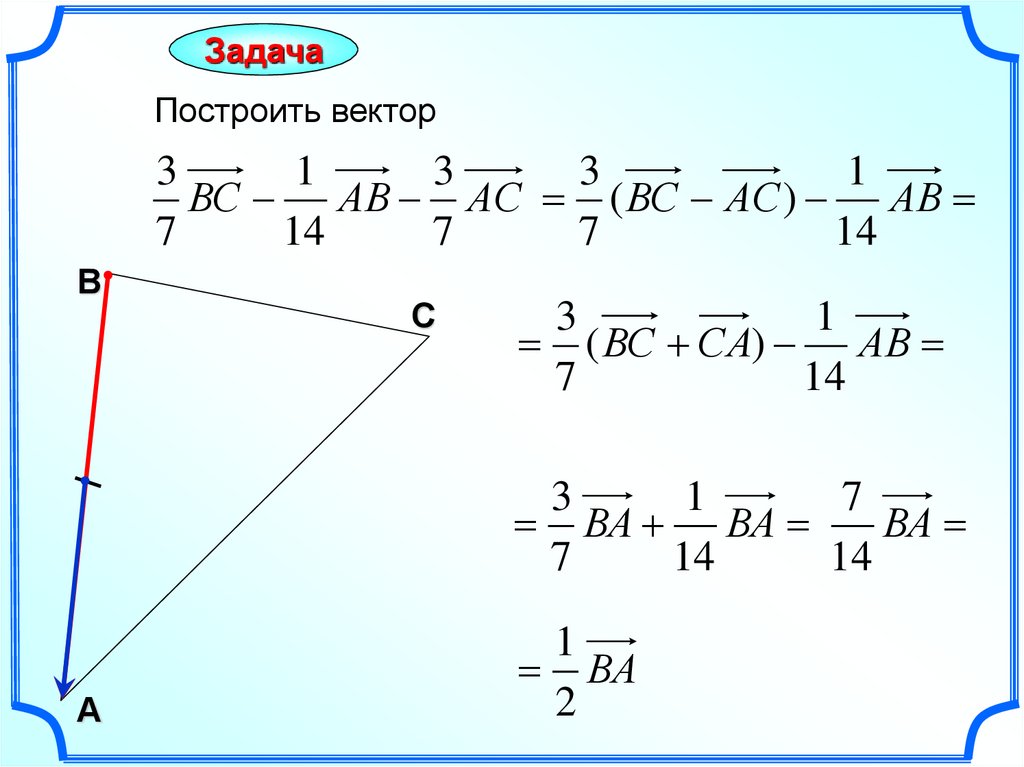
Задача
Построить вектор
3
1
3
3
1
ВС АВ АС ( ВС АС ) АВ
7
14
7
7
14
В
С
3
1
( ВС СА) АВ
7
14
3
1
7
ВА ВА
ВА
7
14
14
А
1
ВА
2

19.

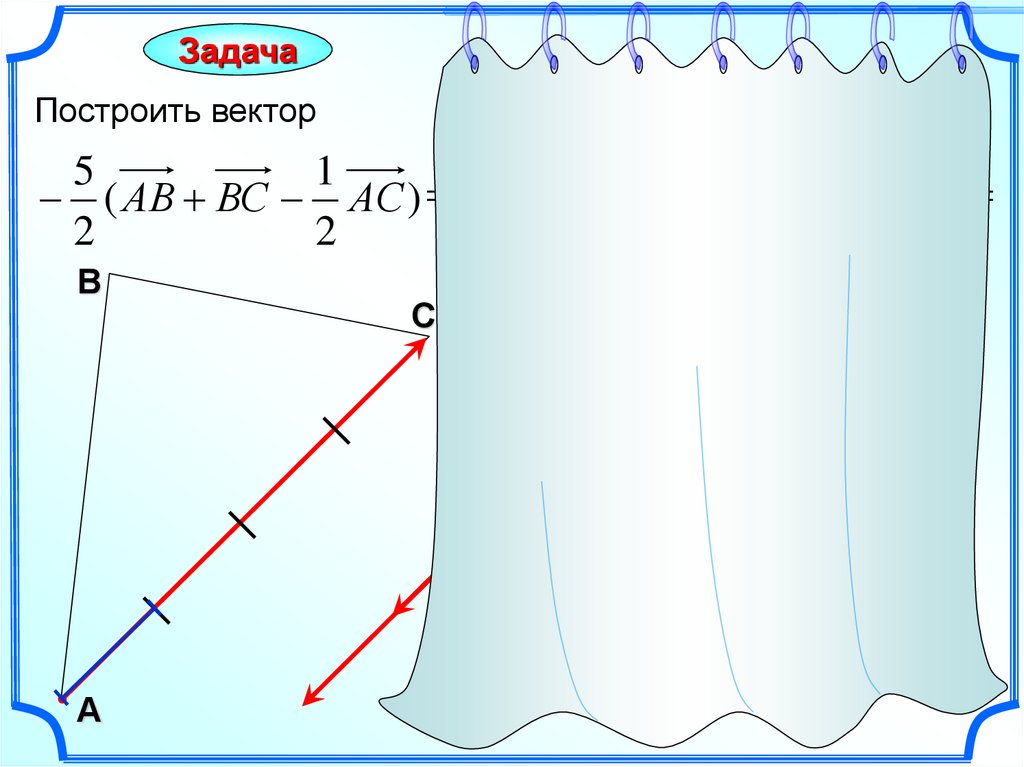
Задача
Построить вектор
5
1
5 1
5
1
( АВ ВС АС ) ( АС АС ) АС
2
2
2 2
2
2
В
5
АС
С
4
А

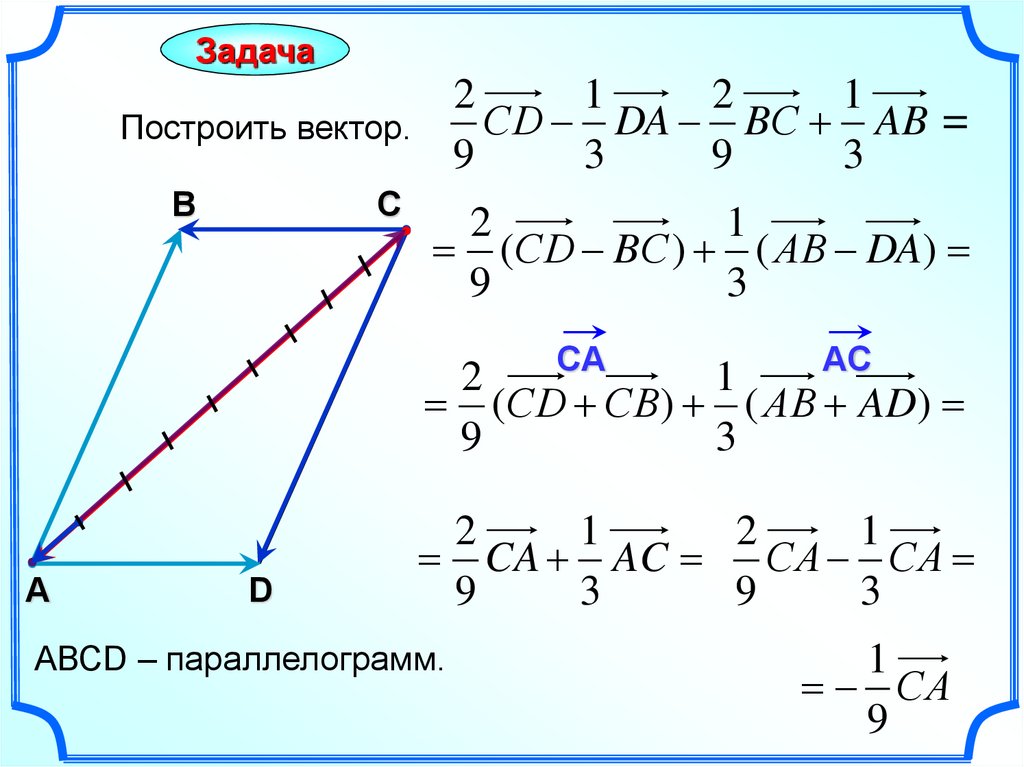
20.

Задача
2
1
2
1
СD DA BС AB =
Построить вектор.
9
3
9
3
В
С
2
1
(СD BС ) ( АВ DA)
9
3
CA
AC
2
1
(СD СB) ( АВ AD)
9
3
А
D
2
1
2
1
CA AC СА СА
9
3
9
3
АВСD – параллелограмм.
1
СА
9

21.

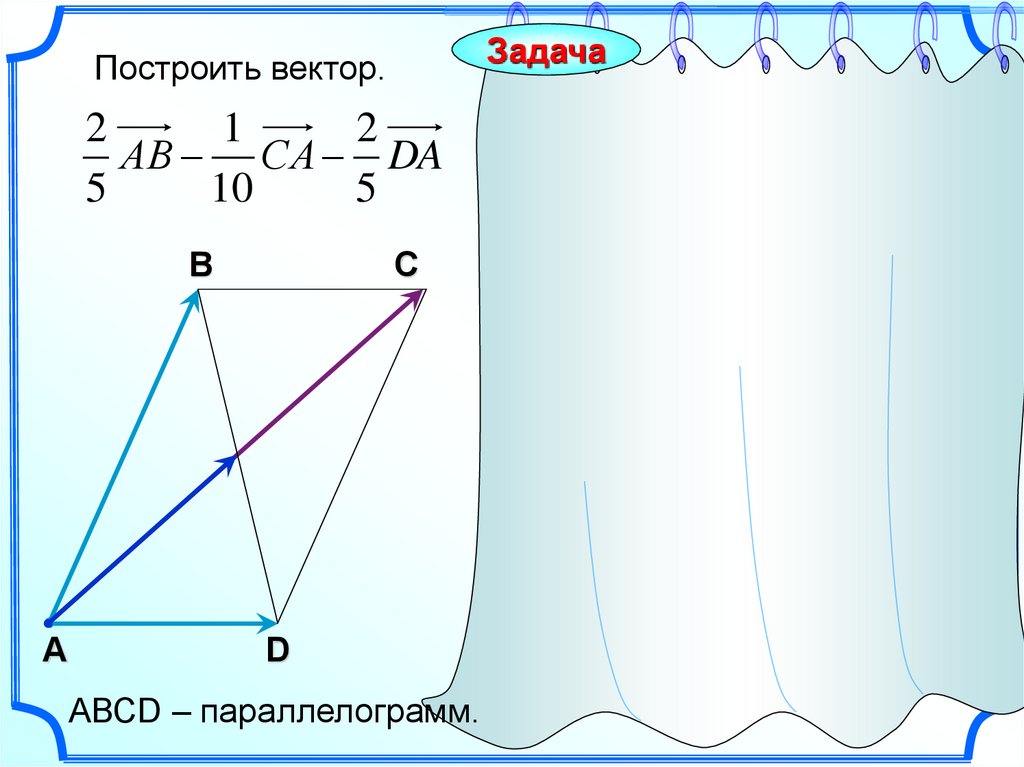
Задача
Построить вектор.
2
1
2
АВ СA DA
5
10
5
В
С
2
1
( АВ DA) CА
5
10
AC
2
1
( АВ AD) CА
5
10
2
1
5
AС AC
АС
5
10
10
А
D
АВСD – параллелограмм.
1
АС
2

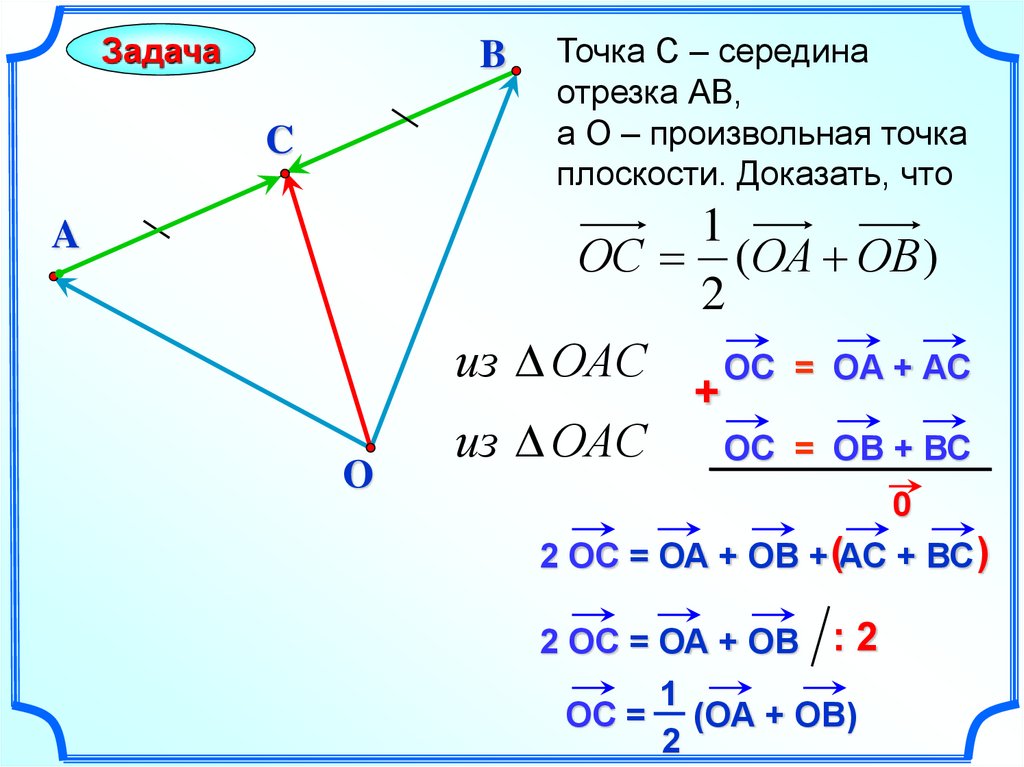
22.

Задача
B
C
Точка С – середина
отрезка АВ,
а О – произвольная точка
плоскости. Доказать, что
1
ОС (ОА ОВ )
2
из ОАС
OС = OА + АС
A
O
из ОАС
+
OС = OВ + ВС
0
2 OС = ОА + ОВ + (АС + ВС )
2 OС = ОА + ОВ : 2
1
OС = (ОА + ОВ)
2

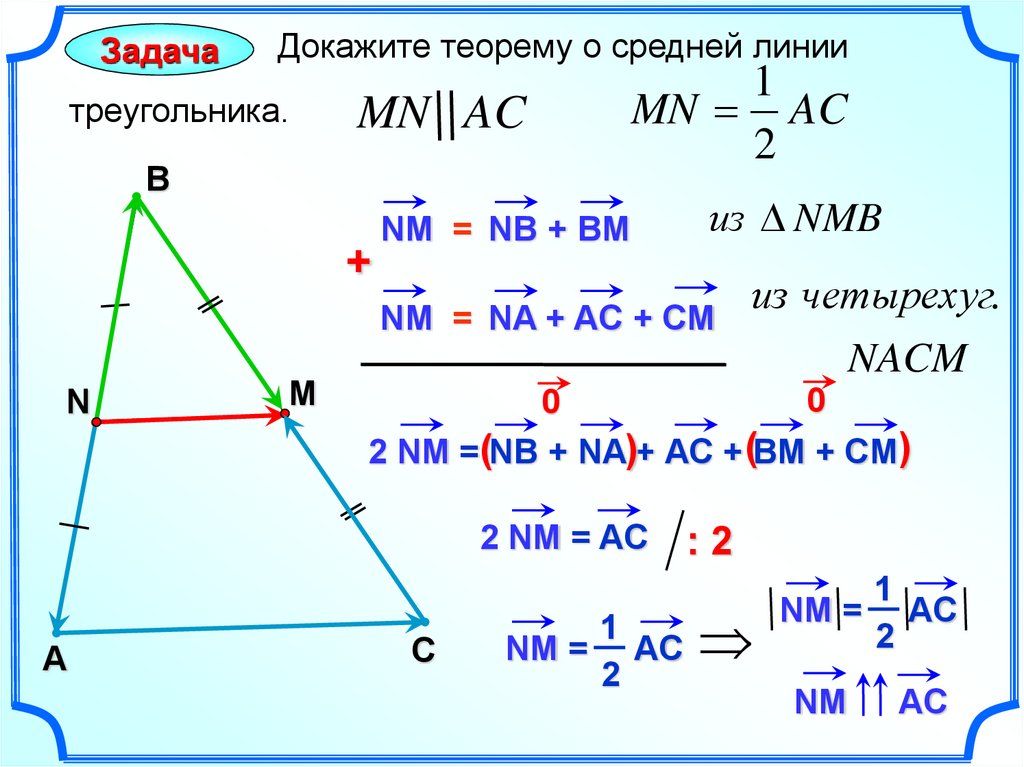
23.

Задача
Докажите теорему о средней линии
треугольника.
1
MN AC
2
MN AC
В
+
N
M
NM = NB + BM
из четырехуг.
NM = NA + AС + CM
NACM
0
0
2 NM =(NB + NA)+ АС + (ВM + CM)
2 NM = AC
A
из NMB
С
NM =
:2
1
AC
2
1
NM = AC
2
NM
AC

24.

Теорема
Средняя линия трапеции параллельна
основаниям и равна их полусумме.
Дано:
трапеция АВСD, MN- средняя линия
Доказать:
MN AD BC
1
MN ( AD BC )
2

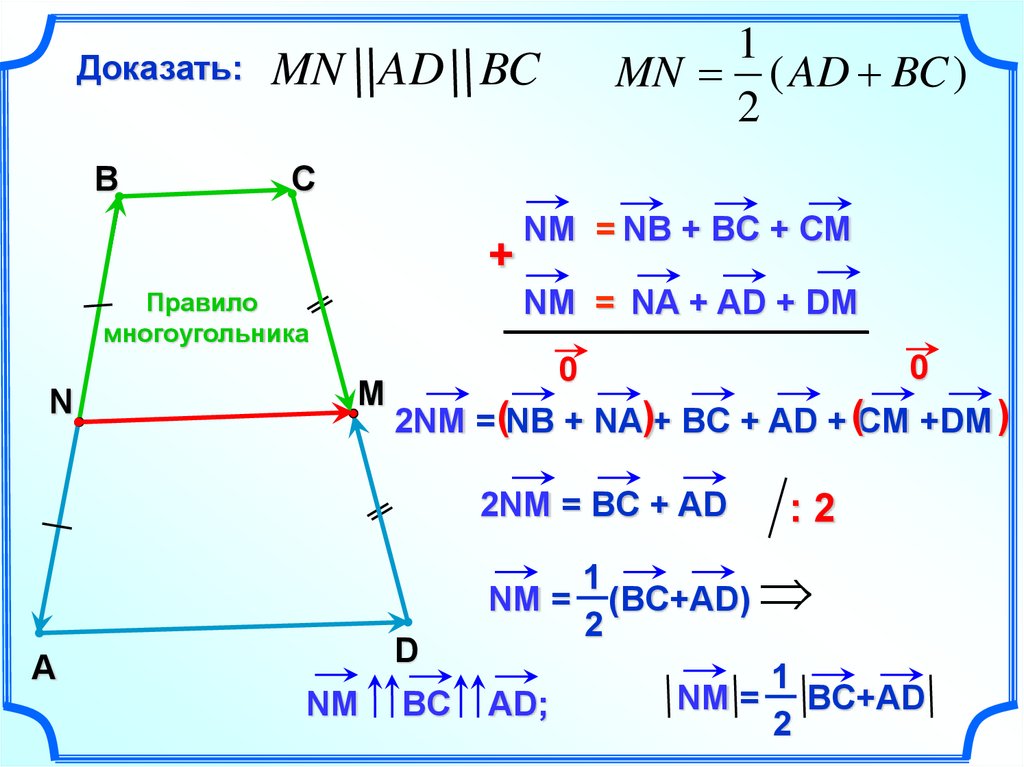
25.

Доказать:
MN AD BC
В
С
+
Правило
многоугольника
N
1
MN ( AD BC )
2
NM = NB + BС + СМ
NM = NA + AD + DM
M
2NM =(NB + NA)+ BС + AD + (CM +DM )
D
A
NM
0
0
BC
2NM = ВC + AD
:2
1
NM = (BC+AD)
2
AD;
1
NM = BC+AD
2

26.

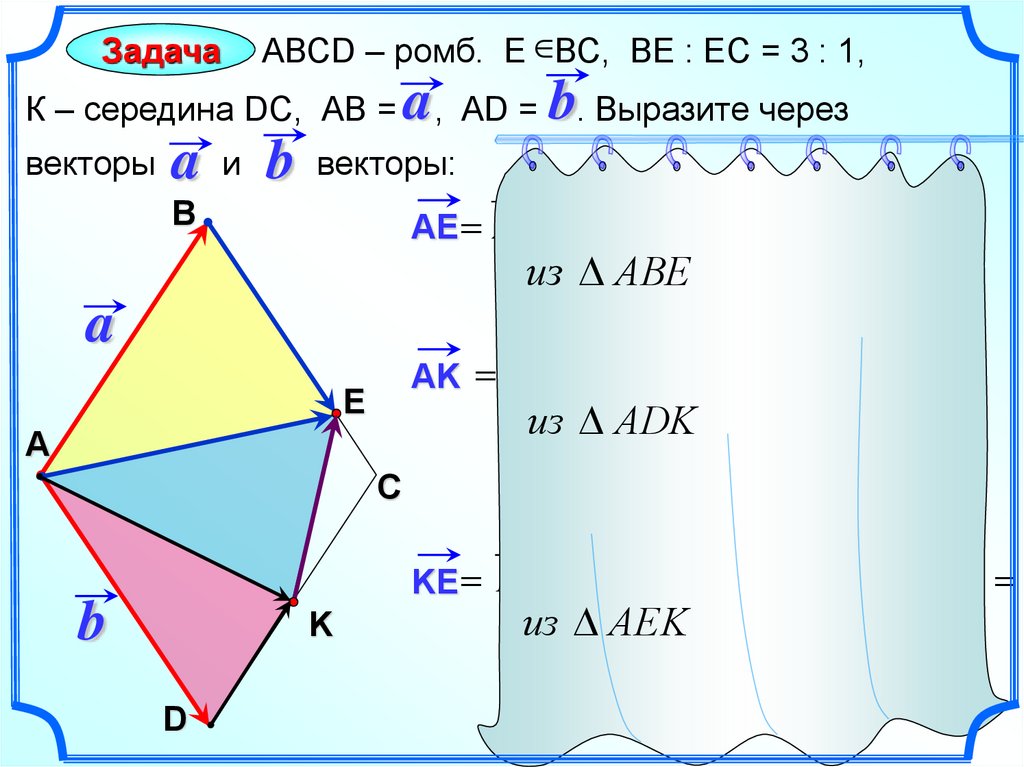
Задача
АВСD – ромб. Е ВС, ВЕ : ЕС = 3 : 1,
К – середина DC, АВ =
векторы
a , AD = b. Выразите через
a и b векторы:
3
3
AE AB BE AB BC a b
4
из АВЕ 4
В
a
E
А
b
K
D
1
AK AD DK AD DС
2
из АDK
1
b a
С
2
1
3
KE KA AE (b a ) (a b)
2
4
из АEK
1
1
a d
2
4

27.

АВ - СВ =
АS - СS =
- ОА - РО =
- MN - LM =
MN - RN =
RP - RP =
- KM + KM =
- KZ + KZ =
- KM + OM =
- ED + KD =
MK + КO + OP + PR =
SK + КV + VP + PM =
3
1
3
ВС АВ АС
7
14
7
2
1
2
1
СD CB AD AB
9
3
9
3