Similar presentations:
Анализ кредитных операций. (Тема 7)
1.
Тема 7. Анализкредитных операций
2.
Доходы от финансово-кредитных операций иразличных коммерческих сделок могут
представать в виде:
процентов,
комиссионных,
дисконта при учете векселей,
дохода от ценных бумаг (дивиденда,
платежа по купону, курсовой разности).
Причем в одной операции может быть
предусмотрено несколько видов дохода.
3.
При получении кредита должник можетоплачивать комиссионные или другие
разовые расходы (посреднику),
которые увеличивают цену кредита, но
не меняют доходность кредитора.
4. 7.1. Долгосрочные кредиты
Рассмотрим баланс долгосрочнойфинансово-кредитной операции,
используя контур финансовой
операции (начисление процентов по
сложной ставке).
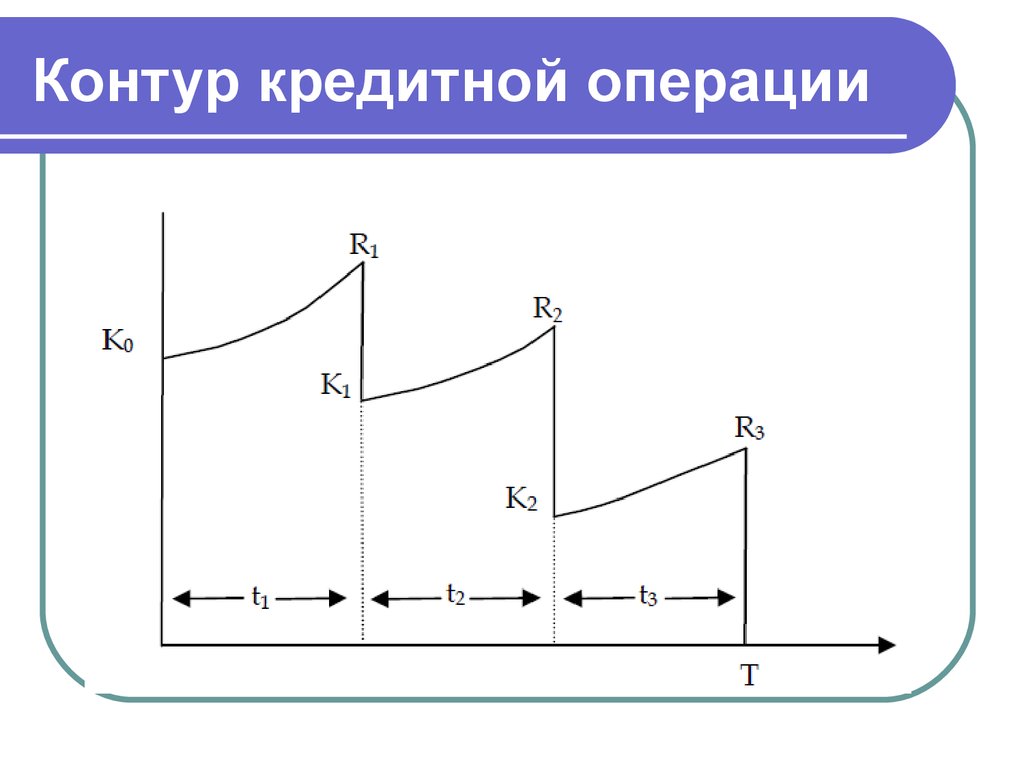
5. Контур кредитной операции
6. Расчетные формулы для контура
где K0 – первоначальная сумма долга,R1 и R2 –промежуточные платежи,
R3 – последний платеж.
Последнее уравнение является балансовым
7.
Выразим K2 через K0 и подставим его вбалансовое уравнение
(1)
8.
В уравнении (1) представлены два процесса:1. наращение первоначальной задолженности
за весь период
2. наращение погасительных платежей за срок
от момента платежа до конца срока
операции.
полученное уравнение отражает баланс сумм,
наращенных на момент времени T.
9.
Умножим уравнение (1) на дисконтныймножитель vT
(2)
В этом виде уравнение выражает равенство
суммы современных величин
погасительных платежей сумме кредита, т.е.
баланс современных величин.
10. Уравнения (1) и (2) нетрудно обобщить на случай n погасительных платежей.
Методы оценки показателей доходности дляразных видов ссудно-кредитных операций
основываются на соответствующем
балансовом уравнении.
Если погасительные платежи осуществляются
периодически постоянными или
переменными суммами, то они образуют
постоянную или переменную ренту,
параметры которых могут быть рассчитаны
обычным образом.
11.
7.2. Доходность ссудных и учетныхопераций с удержанием
комиссионных.
12. Ссудные операции
За открытие кредита, учет векселей идругие операции кредитор часто
взимает комиссионные, которые
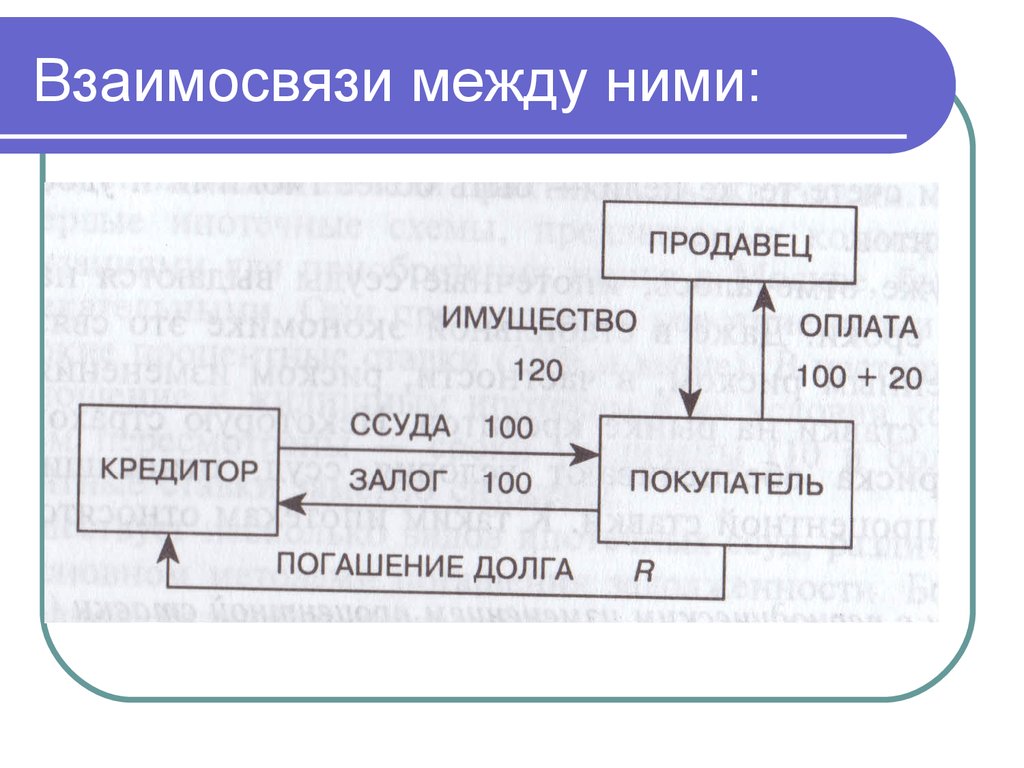
повышают доходность операций, т.к.
размер фактически выданной ссуды
сокращается.
13.
Пусть ссуда в размере D выдана насрок n, и при ее выдаче из нее
удерживаются комиссионные в
размере G.
Фактически выданная ссуда равна D-G.
14. 1) сделки с начислением простых процентов по ставке i
Пустьiэ,пр – фактическая доходность,
выраженная через ставку простых
процентов,
g – относительная величина
комиссионных в сумме кредита (G=Dg)
15. Из балансового уравнения
16.
2) долгосрочная операция, когда ссуда судержанием комиссионных выдается
под сложные проценты.
Тогда балансовое уравнение:
17.
Из G=Dg18. Учетные операции
Рассмотрим полную доходность банкапри осуществлении операции учета с
удержанием комиссионных.
19.
Пусть при учете применяется простаяучетная ставка.
После удержания комиссионных и
дисконта заемщик получает сумму
D-Dnd-G.
Если G=Dg, то эта сумма составит
D(1-nd-g).
20.
Тогда балансовое уравнениеполная доходность:
21.
Пусть при учете применяется сложнаяставка.
Выразить iэ через уравнение
эквивалентности. ….
22. 7.3. Форфейтная кредитная операция
Эта операция получила распространение вовнешней торговле, но может применяться и
во внутренней торговле страны.
Потребность в такой операции возникает
когда покупатель приобретает товар не
имея соответствующих денежных средств, а
продавец также не может продать товар в
кредит.
23.
Форфейтная кредитная операция(операция форфэ) - операция, в
которой участвуют продавец,
покупатель и банк-кредитор.
24.
В рамках форфейтной операциипокупатель выписывает комплект
векселей на сумму, равную стоимости
товара плюс проценты за кредит,
который формально предоставляется
покупателю продавцом.
Сроки векселей равномерно
распределены во времени обычно
через равные интервалы (полугодия).
25.
Продавец сразу же после полученияпортфеля векселей учитывает его в
банке без права оборота на себя,
получая полностью деньги за свой
товар.
26.
Банк, форфетируя сделку, берет весьриск на себя.
Иногда в качестве четвертого агента
сделки может выступать банк
покупателя, гарантирующий
погашение задолженности по
векселям.
27.
Т.к. платежи по векселям представляютсобой постоянную ренту, то и расчет
таких операций опирается на уже
полученные нами результаты.
28.
Цель продавца –получить деньги в начале сделки и тем
самым устранить риск отказа
покупателя от платежей и риск,
связанный с колебанием процентных
ставок по кредиту.
29.
Цель покупателя –приобрести продукцию в кредит с
наименьшими совокупными
издержками.
Расходы покупателя заключаются в
погашении последовательно
предъявляемых ему векселей.
30.
Для банка форфейтная операция обычная операция учета портфелявекселей. Эффективность этой
операции определяется размером
учетной ставки и рядом других
параметров
31. Анализ позиции продавца
Продавец должен получить при учетевекселей сумму, равную цене товара.
Сумма, проставленная на векселе Vt,
состоит из двух элементов:
1) суммы, погашающей основной долг
(цену товара),
2) процентов за кредит:
32.
а) проценты на остаток задолженности;в этом случае срок, за который они
начисляются, начинается с момента
погашения предыдущего векселя;
б) проценты на ту часть долга, которая
покрывается векселем; в этом случае
срок исчисляется от начала сделки и
до момента погашения векселя.
33.
Пусть долг погашается равными суммами;n - число векселей или периодов;
i - ставка простых процентов за период, под
которую производится кредитование;
d - простая учетная ставка, используемая
банком при учете векселей;
Р - цена товара (если условия операции
предусматривают выплату аванса, то
последний вычитается из цены и далее не
принимается во внимание; иначе говоря, под
Р будем понимать цену за вычетом аванса).
34. Вариант а.
Погашение основного долгапроизводится равными суммами,
соответственно в каждый вексель
записывается сумма Р/n. Проценты за
кредит образуют ряд:
35.
Сумма векселя, погашаемого в момент t:36.
Общая сумма начисленных процентов:(*)
Общая сумма векселей:
37. Вариант б.
По определениюСумму процентов за весь срок
38. Вывод
Сумма процентов в обоих вариантахрасчета одинакова. Однако
распределение платежей во времени
противоположное: в варианте а они
уменьшаются, в варианте б - растут.
Для покупатепя вариант б на первый
взгляд представляется более
привлекательным.
39. Корректировка условий продажи
При учете портфеля векселей в банкепродавец получит некоторую сумму А.
Если применяется простая учетная
ставка, то современная величина всех
платежей по векселям
40. Вариант а
41. Пусть сумма в квадратных скобках - z.
42.
Если Z < 1, то продавец получит сумму,которая меньше договорной цены Р.
Наиболее простой путь избежать потерь повысить цену в 1/z раз.
Такой корректировочный множитель позволяет
точно определить необходимую поправку и,
кроме того, дает возможность проследить
влияние всех воздействующих факторов.
Когда Z = 1 - нет необходимости в
корректировке, продавец получает при учете
векселей оговоренную сумму.
43.
Представляет практический интерессоотношение процентных ставок, при
которых продавец не будет нести
потери. Это выполнимо в случае,
когда
i - d = id(n + 2)/3
44.
Тогда барьерная процентная ставка,при которой отпадает необходимость
в корректировке цены:
45. ПРИМЕР
Каков должен быть уровень процентнойставки за кредит для того, чтобы
покупатель не понес ущерба в
операции а форфэ при условии, что d
= 4,75 (данные примера 1, вариант а
расчета сумм векселей)?
46. Решение
повышение годовой ставки кредита до10,4972 полностью компенсирует потерю
продавца. Альтернативой может служить
повышение цены товара
47. Вариант б
Проценты начисляются на ту часть долга,которая погашается векселем. По
определению
Корректирующий цену множитель- 1 / z.
48. ПРИМЕР
Определить корректирующиймножитель к цене по данным примера
1 (вариант б) при условии, что d =
4,75.
49. Решение
50.
Единственное значение i, при которомпродавец не терпит убытки в варианте
б, при Z = 1. Для этого необходимо
выполнение условия
51.
52. Пример
По данным примера 1 (вариант б) и приусловии, что d = 4,75 найти барьерную
процентную ставку.
53. Решение
54.
Таким образом, у покупателя имеютсядве возможности для компенсации
потерь при учете портфеля векселей повысить цену товара на 1,0116977
или увеличить ставку за кредит до
11,0787 годовых.
55. 7.4. Ипотечные ссуды
Ссуды под залог недвижимости, илиипотеки, получили широкое
распространение в странах с развитой
рыночной экономикой.
В такой сделке владелец имущества
получает ссуду у залогодержателя.
56.
В случае, если владелец имуществаотказывается от погашения ссуды или
не полностью погашает задолженность,
то залогодержатель имеет право
возместить ущерб из стоимости
заложенного имущества.
57.
Сумма ссуды обычно несколько меньшеоценочной стоимости закладываемого
имущества.
Объекты залога:
жилые дома,
фермы,
земля,
другие виды недвижимости.
58.
Ипотечные ссуды выдаются:коммерческими банками
специальными ипотечными банками,
ссудо-сберегательными
ассоциациями.
Характерной особенностью ипотечных
ссуд является длительный срок
погашения – в СШАдо 30 и более лет.
59.
Т.к. платежи по обслуживанию долга (поуплате процентов и погашению
предоставленного кредита), являются
регулярными, то и расчет ипотеки
сводится к расчету параметров того
или иного вида ренты.
Основной задачей расчета является
разработка планов погашения и
остатка задолженности на любой
момент времени.
60.
Существует несколько видов ипотечныхссуд, различающихся в основном
методами погашения задолженности.
61. Виды ипотечных ссуд
Стандартная ипотекаЗаемщик получает от залогодержателя,
(кредитора), некоторую сумму под залог
недвижимости.
1)
Этот кредит он погашает вместе с процентами
равными, обычно ежемесячными,
взносами (пренумерандо или
постнумерандо).
В договоре обычно устанавливается
ежемесячная ставка процента, реже –
годовая номинальная.
62.
В осуществлении ипотеки при покупке(строительстве) объекта залога
участвует три агента:
продавец,
покупатель (должник),
заимодавец (кредитор).
63. Взаимосвязи между ними:
64.
Продавец получает от покупателя занекоторое имущество полную его стоимость
(120).
Для этого покупатель получает ссуду под
залог этого имущества (100) и добавляет
собственные средства (20).
Задача заключается в определении размера
ежемесячных погасительных платежей R и
остатка задолженности на момент
очередного ее погашения вплоть до полной
оплаты долга
65.
Для месячных взносов постнумерандо:где D - сумма ссуды;
N - общее число платежей,
N= 12n (nсрок погашения в годах);
i - месячная ставка процента;
R - месячная сумма взносов;
а n;i - коэффициент приведения постоянной
ренты.
66.
Величина взносагде с =1/ а n;i - коэффициент
рассрочки.
67.
Для рент пренумерандо68. 2) Ссуды с ростом платежей (схема GPM – Graduated Payment Mortgage)
Предусматривается постоянный рострасходов по обслуживанию долга в первые
5-10 лет.
Затем погашение производится
постоянными взносами.
Расчет сводится к применению формул
для рент с переменными и постоянными
платежами в соответствующие интервалы
времени.
69. 3) Ссуды с периодическим увеличением взносов
(схема SRM - Step Rate Mortgage)По согласованному графику каждые 3-5 лет
сумма взносов увеличивается. Весь срок
ипотеки разбит на k периодов (равные или
неравные). Размеры взносов в каждом
периоде – R1, R2, …, Rk-1.
Задача состоит в том, чтобы определить
размер последнего взноса Rk
Поток платежей представляет собой
последовательность постоянных рент.
70. 4) Ссуда с льготным периодом
Предполагается наличие льготногопериода, в течение которого
выплачиваются только проценты по
долгу.
71. 5) Ссуда с залоговым счетом
Клиент в начале операции вносит наспециальный (залоговый) счет
некоторую сумму денег.
На начальных этапах он выплачивает
кредитору погасительные взносы,
которые меньше тех, что необходимы
по стандартной ипотеке.
72.
Недостающие суммы добавляютсяпутем списания с залогового счета,
пока он не иссякнет.
Таким образом кредитор все время
получает постоянные взносы (как в
стандартной ипотеке). А взносы
должника характеризуются ростом во
времени.
73. 6) Ссуды с периодическим изменением процентной ставки
Стороны каждые 3-5 летпересматривают уровень процентной
ставки с целью адаптации к условиям
рынка.
74. 7) Ссуда с переменной процентной ставкой
Уровень ставки привязывается к какомулибо распространенномуфинансовому показателю или индексу.
Пересмотр обычно осуществляется по
полугодиям.
Чтобы избежать чрезмерных скачков,
предусматривается верхняя и нижняя
границы разовых корректировок
(например, не более 2%).
75. 8) Ипотека с обратным аннуитетом
Предназначена для заклада домовпожилыми владельцами (продажа в
рассрочку с правом дожития).
Цель такого залога – получение
систематического дохода владельцем
жилища.
76. 7.5. Льготные займы и кредиты
В ряде случаев долгосрочные займы икредиты выдаются на льготных для
заемщика условиях.
Низкая процентная ставка по сравнению с
рыночной в сочетании с большим сроком
и наличием льготного периода дают
должнику существенную выгоду, которую
можно рассматривать как субсидию
77.
Она оказывается как на международномуровне в рамках финансовой помощи
развивающимся странам, так и внутри
страны для поддержки отдельных
отраслей или производств.
Проблема определения размера этой
помощи сводится к оценке
грант-элемента.
78.
Грант-элемент – это условная субсидиякредитора, связанная с применением
более низкой процентной ставки.
Грант-элемент определяется в двух
видах: в виде абсолютной и
относительной величины
79. Абсолютный грант-элемент -
Абсолютный грант-элемент разность суммы займа и современнойвеличины платежей по погашению займа.
W=D-G
Проблема здесь состоит в выборе ставки
процентов для расчета современной
величины платежей.
Обычно используют ставку, применяемую на
рынке долгосрочных кредитов.
80. Относительный грант-элемент
где W – абсолютный грант-элемент,w – относительный грант-элемент,
D – сумма кредита,
G – современная величина платежей,
рассчитанная по реальной ставке рынка
кредитов.
81.
Пусть долг и проценты выплачиваются ввиде постоянных срочных уплат.
Пусть заем выдан на n лет и
предусматривает выплату процентов
по льготной ставке g.
На денежном рынке аналогичные по
сроку и величине займы выдаются по
ставке i.
82.
В этом случае при отсутствии льготногопериода срочная уплата составит:
а современная величина всех выплат
должника очевидно равна Yаn;i
83.
Тогдагде аn;i и an;g - коэффициенты приведения
постоянных годовых рент постнумерандо,
определенные для процентных ставок i и g,
i > g.
84. Пример
Льготный заем выдан на 10 лет под3,8%. Предусматривается погашение
долга равными срочными уплатами.
Известно, что обычная рыночная
ставка для такого срока займа равна
8%. Найти относительный грантэлемент.
Четыркин стр. 197




















































































 finance
finance