Similar presentations:
Отображение Пуанкаре
1. Отображение Пуанкаре
2. Жюль Анри́ Пуанкаре́ (1854−1912) Французский математик, физик, астроном и философ. Глава Парижской академии наук (1906), член
3.
Пуанкаре предложил ставший классическим метод анализа динамических систем.Этот метод позволяет заменить потоковую систему n-го порядка на отображение
(n-1)-го порядка с дискретным временем, называемое отображением Пуанкаре.
4. Определение
Отображение Пуанкаре для неавтономных системПеридическая во времени неавтономная система n-го порядка с минимальным
периодом T может быть преобразована в автономную систему (n+1)-го порядка в
цилиндрическом фазовом пространстве с помощью преобразования
5.
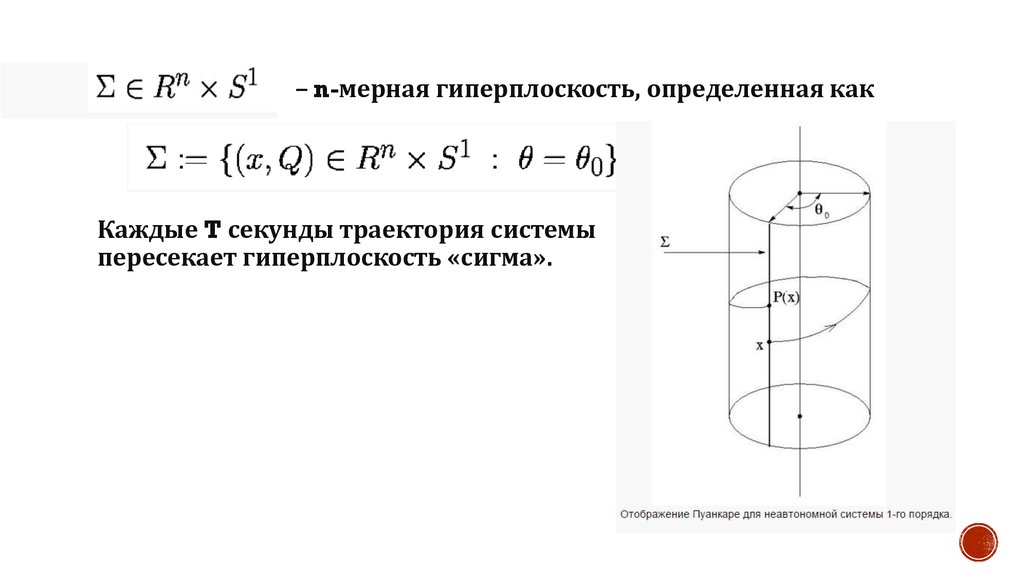
− n-мерная гиперплоскость, определенная какКаждые T секунды траектория системы
пересекает гиперплоскость «сигма».
6.
Получаемое отображениеОпределяется как:
где
− отображение Пуанкаре неавтономной системы, на
которую указывает индекс N
7.
можно представлять себе двумя способами:1.
показывает, какое значение примет x через T секунд.
Это называется отображением сдвига на время Т.
2.
Орбита
моделирует отдельную траекторию с интервалом в T секунд, т.е.
8.
Отображение Пуанкаре для автономных системЗамечания:
1. PA определено локально, то есть, в окрестности
x*. В отличие от неавтономного случая, здесь нет
гарантии, что траектория, вышедшая из точки на
"сигма" снова пересечет "сигма".
2. Для эвклидова фазового пространства, точка
PA(x) не является первой точкой, в которой поток
фt пересечет "сигма"; фt(x) должен пройти через
"сигма" по крайней мере еще один раз, прежде чем
возвратиться в U. В этом, также, заключается
отличие от цилиндрического фазового
пространства.
3. PA является диффеоморфизмом и,
следовательно, обратимо и дифференцируемо.
9.
На практике выбирают (n-1)-мерную гиперплоскость "сигма", которая разделяет RNна две области:
где h есть вектор, нормальный к "сигма" и x - некоторая точка, лежащая на
гиперплоскости, и
-
скалярное произведение. Если "сигма" выбрана правильно, то наблюдаемая
траектория будет повторно пересекать "сигма", переходя из "сигма-" в "сигма+", и
затем обратно
10.
P+: P+(x) - это точка, в которой фt(x) первый раз пересекает "сигма" вположительном направлении, т.е.
P-: P-(x) - это точка, в которой фt(x) первый раз пересекает "сигма" в
отрицательном направлении, т.е.
P+-: P+-(x) - это первая точка, в которой фt(x) пересекает "сигма" в каком-либо
направлении при t>0.
P+ и P- называются односторонними отображениями Пуанкаре, в то время как P+называется двусторонним отображением Пуанкаре. Отметим, что точка, в которой
траектория касается гиперплоскости, т.е. x на "сигма", для которой
удовлетворяет критериям каждого из трех отображений.
11.
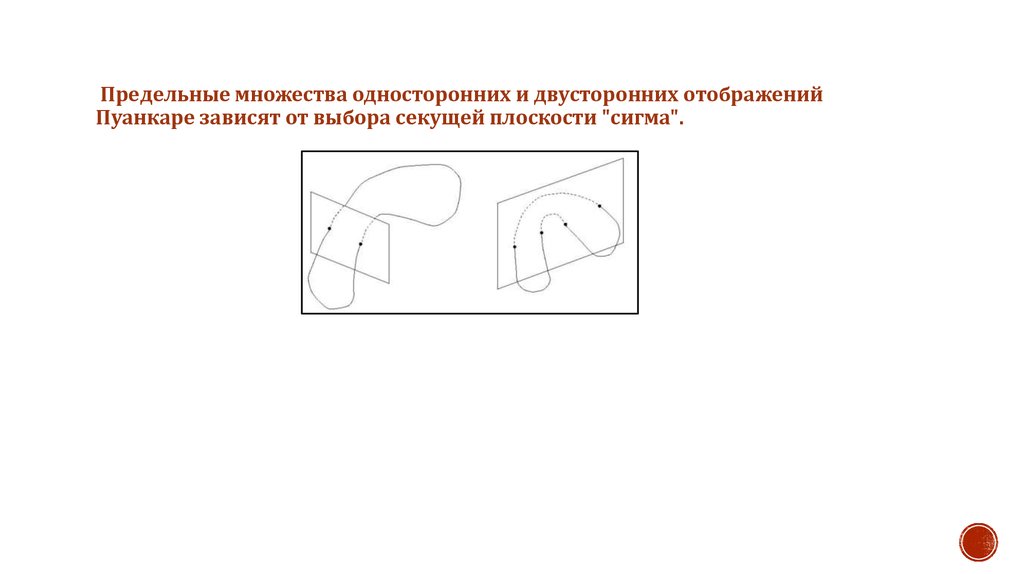
Предельные множества односторонних и двусторонних отображенийПуанкаре зависят от выбора секущей плоскости "сигма".









 mathematics
mathematics








