Вычисление электрических полей с помощью теоремы Остроградского-Гаусса

1.

Лекция 4. Вычисление электрических
полей с помощью теоремы
Остроградского-Гаусса
4. Вычисление электростатических полей с помощью
теоремы Остроградского - Гаусса
4.1. Поле бесконечной однородно заряженной
плоскости
4.2. Поле двух равномерно заряженных плоскостей
4.3. Поле заряженного бесконечного цилиндра (нити)
4.4. Поле двух коаксиальных цилиндров с одинаковой
линейной плотностью заряда, но разным знаком
4.5. Поле заряженного пустотелого шара
4.6. Поле объемного заряженного шара

2.

4.1. Поле
бесконечной однородно заряженной
плоскости
Поверхностная плотность заряда на
произвольной плоскости площадью S
определяется по формуле:
dq
σ
,
dS
dq – заряд, сосредоточенный
на площади dS;
dS – физически бесконечно
малый участок поверхности.

3.

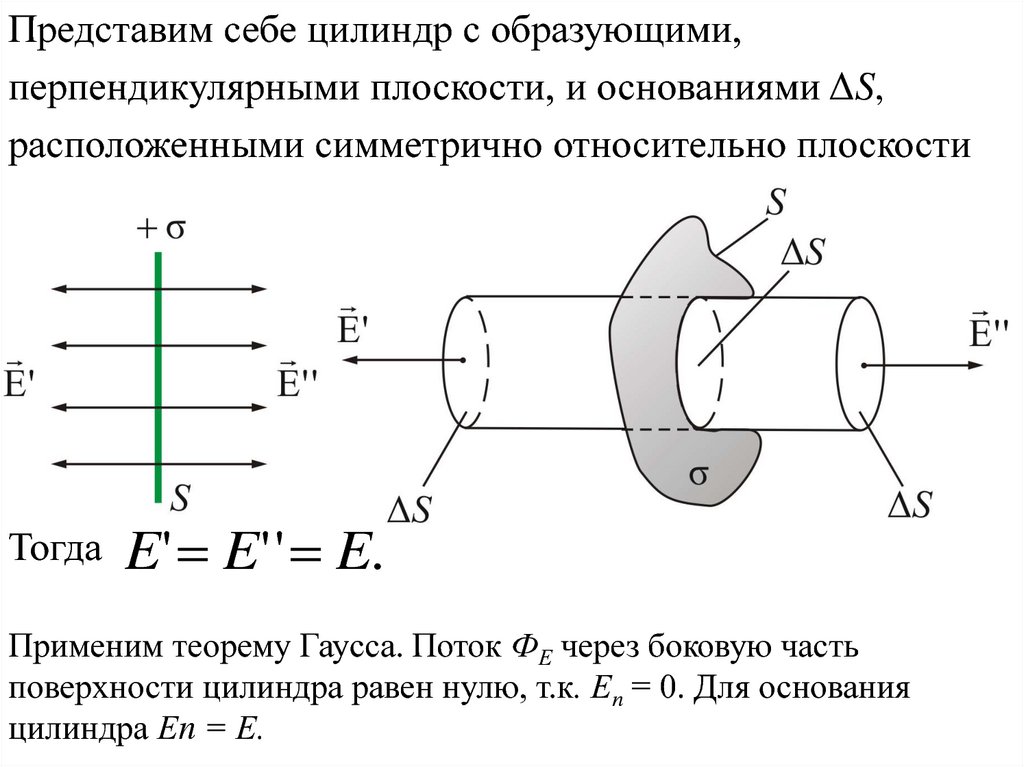
Представим себе цилиндр с образующими,
перпендикулярными плоскости, и основаниями ΔS,
расположенными симметрично относительно плоскости
Тогда
E ' E ' ' E.
Применим теорему Гаусса. Поток ФЕ через боковую часть
поверхности цилиндра равен нулю, т.к. Еn = 0. Для основания
цилиндра Еn = Е.

4.

Суммарный поток через замкнутую поверхность
(цилиндр) будет равен:
ФЕ 2ΔSE.
Внутри поверхности заключен заряд .
Следовательно, из теоремы ОстроградскогоГаусса получим:
ФЕ
q
0
; тогда 2 SE S
1
0
откуда видно, что напряженность поля плоскости S
равна:
(4.1)
σ
E
.
2ε 0

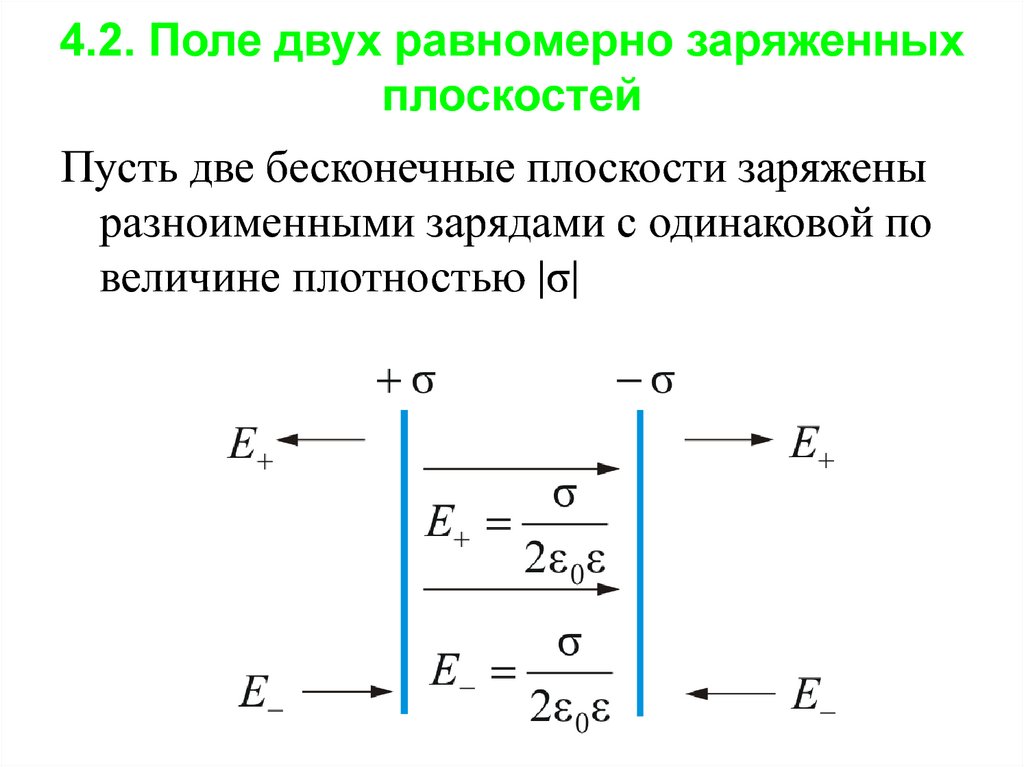
5. 4.2. Поле двух равномерно заряженных плоскостей

Пусть две бесконечные плоскости заряжены
разноименными зарядами с одинаковой по
величине плотностью |σ|

6.

Результирующее поле, как было сказано выше,
находится как суперпозиция полей, создаваемых
каждой из плоскостей. Тогда внутри плоскостей
E E E отсюда E σ / ε 0
(4.2)
Вне плоскостей напряженность поля
E 0.
Полученный результат справедлив и для плоскостей
конечных размеров, если расстояние между
плоскостями гораздо меньше линейных размеров
плоскостей (плоский конденсатор).

7.

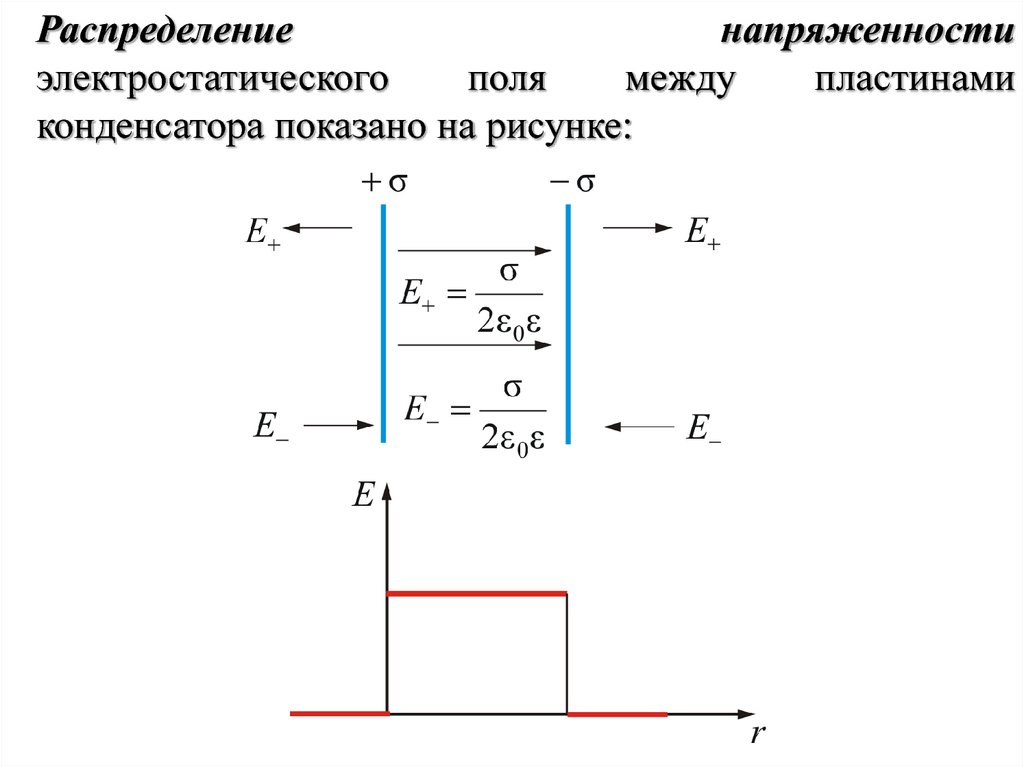
Распределение
напряженности
электростатического
поля
между
пластинами
конденсатора показано на рисунке:

8.

Между пластинами конденсатора действует
сила взаимного притяжения (на единицу
площади пластин):
2
F SσE т.е.
Fед
S
S
σ
Fед
2ε 0 ε
Механические силы, действующие между
заряженными телами, называют
пондермоторными.

9.

S
F
,
2 0
2
Сила притяжения между пластинами конденсатора:
где S – площадь обкладок конденсатора.
Т.к.
Е
q E
0
0
S
(4.3)
ε0 E S
q
F
2ε 0εS
2
Это формула для расчета пондермоторной силы
2
2

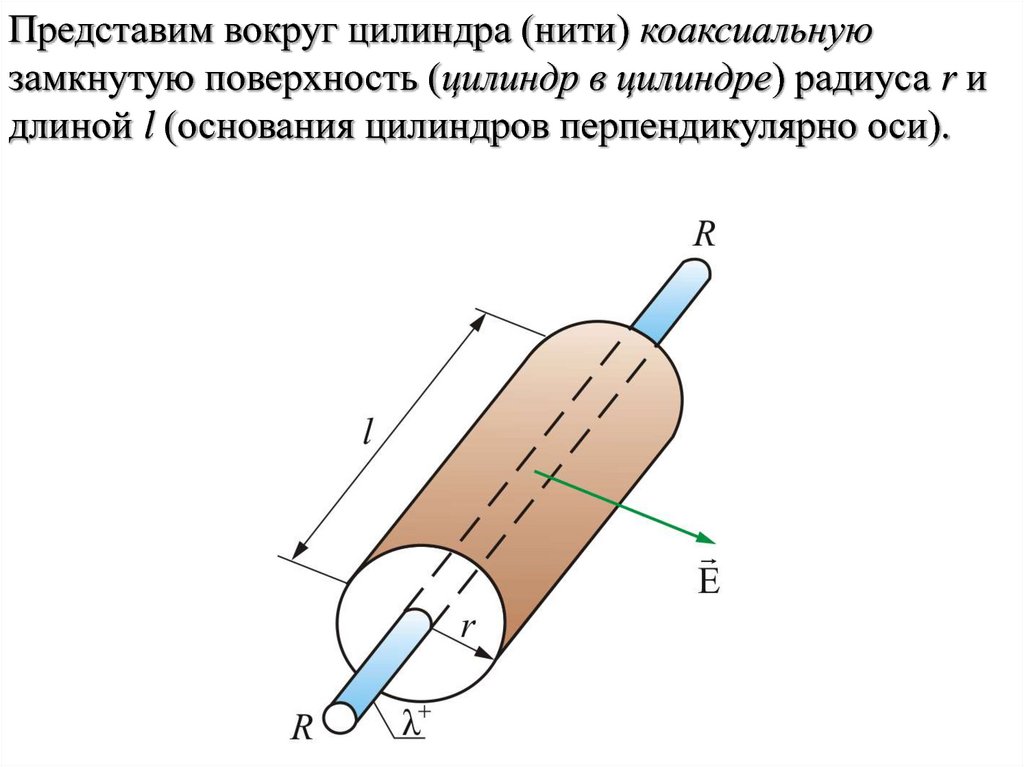
10. 4.3. Поле заряженного бесконечного цилиндра (нити)

Пусть поле создается бесконечной
цилиндрической поверхностью радиуса R,
заряженной с постоянной линейной
плотностью
dq
λ
dl
где dq – заряд, сосредоточенный на отрезке
цилиндра

11.

Представим вокруг цилиндра (нити) коаксиальную
замкнутую поверхность (цилиндр в цилиндре) радиуса r и
длиной l (основания цилиндров перпендикулярно оси).

12.

Для оснований цилиндров
для боковой поверхности
En 0,
En E (r ),
т.е. зависит от расстояния r.
Следовательно, поток вектора через
рассматриваемую поверхность, равен
ФE E (r ) S E (r )2πrl.

13.

При
r R, на поверхности будет заряд
q λl.
По теореме Остроградского-Гаусса
Тогда
λ
Е (r )
при r R
2πε0r
E (r ) 0
Если
то
, т.к.
внутри замкнутой поверхности зарядов нет.
r R,
λl
E (r )2πrl
ε0
(4.4)

14.

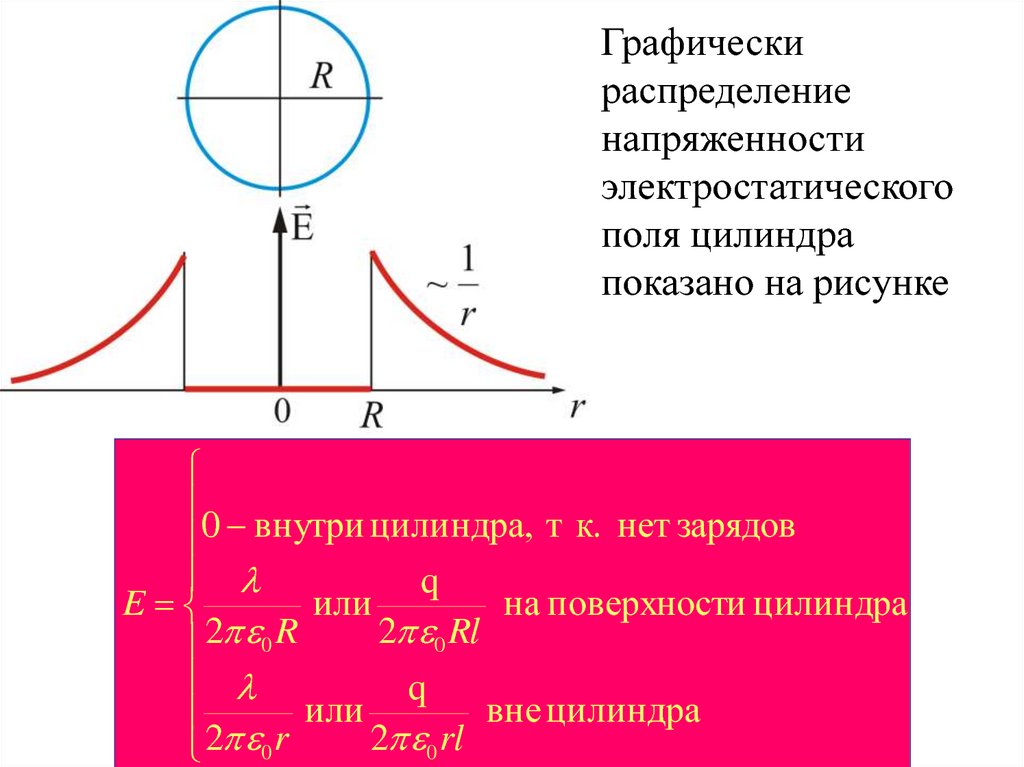
• Графически
распределение
напряженности
электростатического
поля цилиндра
показано на рисунке
0 внутри цилиндра, т к. нет зарядов
q
E
или
на поверхности цилиндра
2 0 Rl
2 0 R
q
или
вне цилиндра
2 0 rl
2 0 r

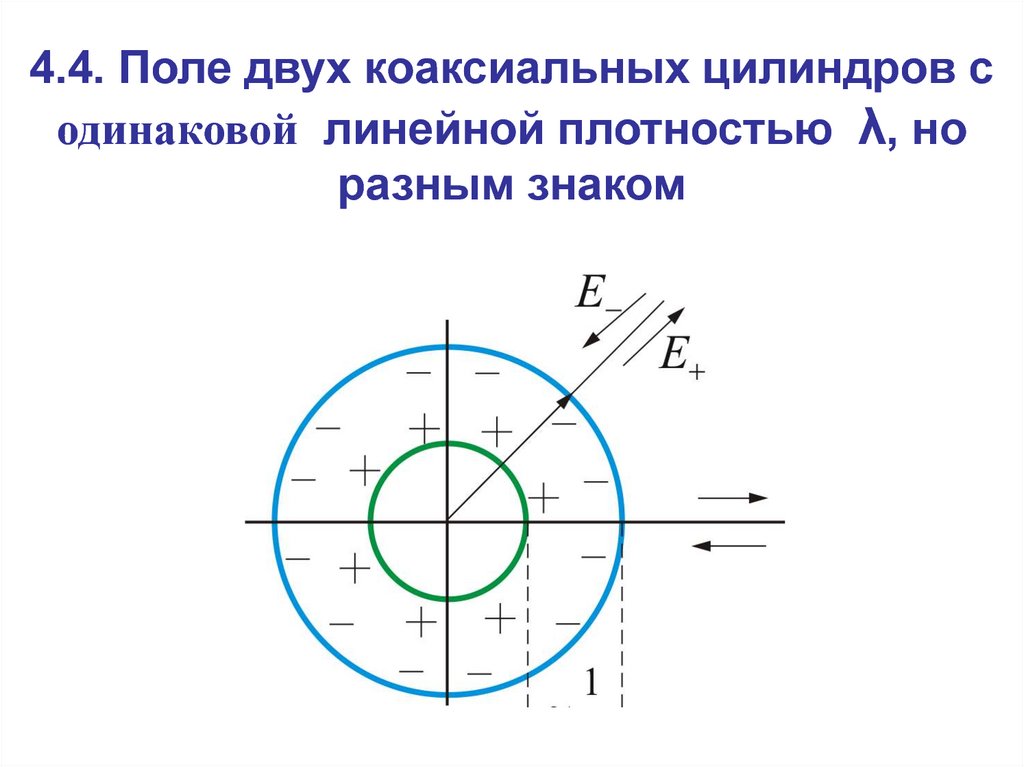
15. 4.4. Поле двух коаксиальных цилиндров с одинаковой линейной плотностью λ, но разным знаком

E 0

16.

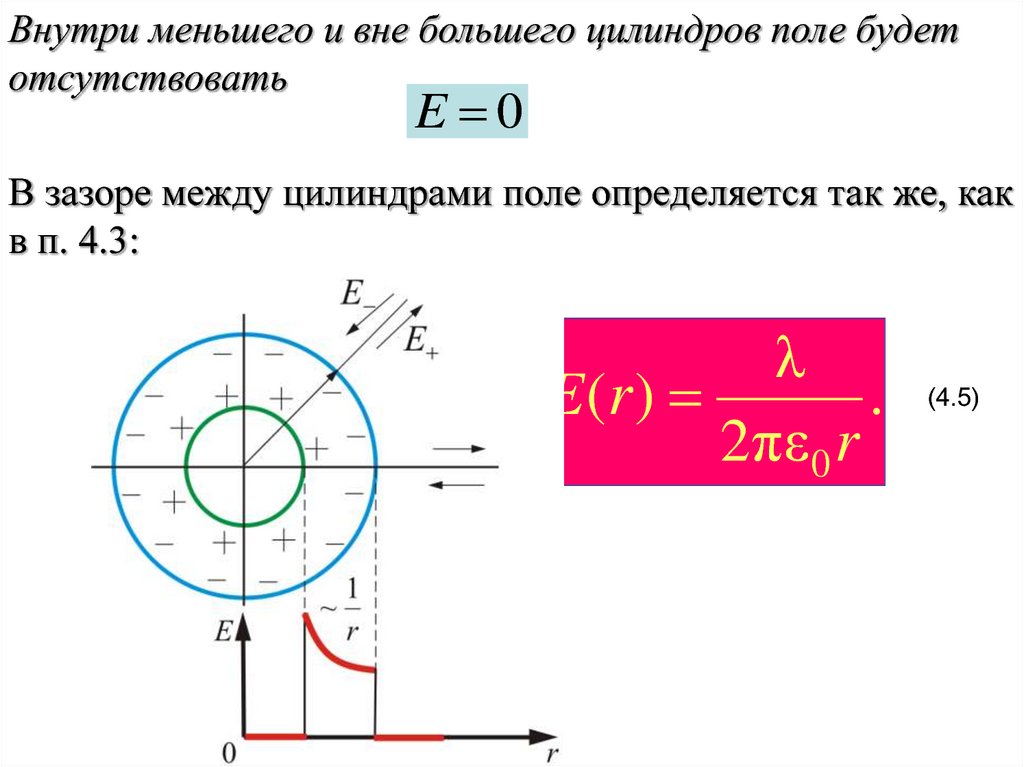
Внутри меньшего и вне большего цилиндров поле будет
отсутствовать
E 0
В зазоре между цилиндрами поле определяется так же, как
в п. 4.3:
λ
E (r )
.
2πε 0 r
(4.5)

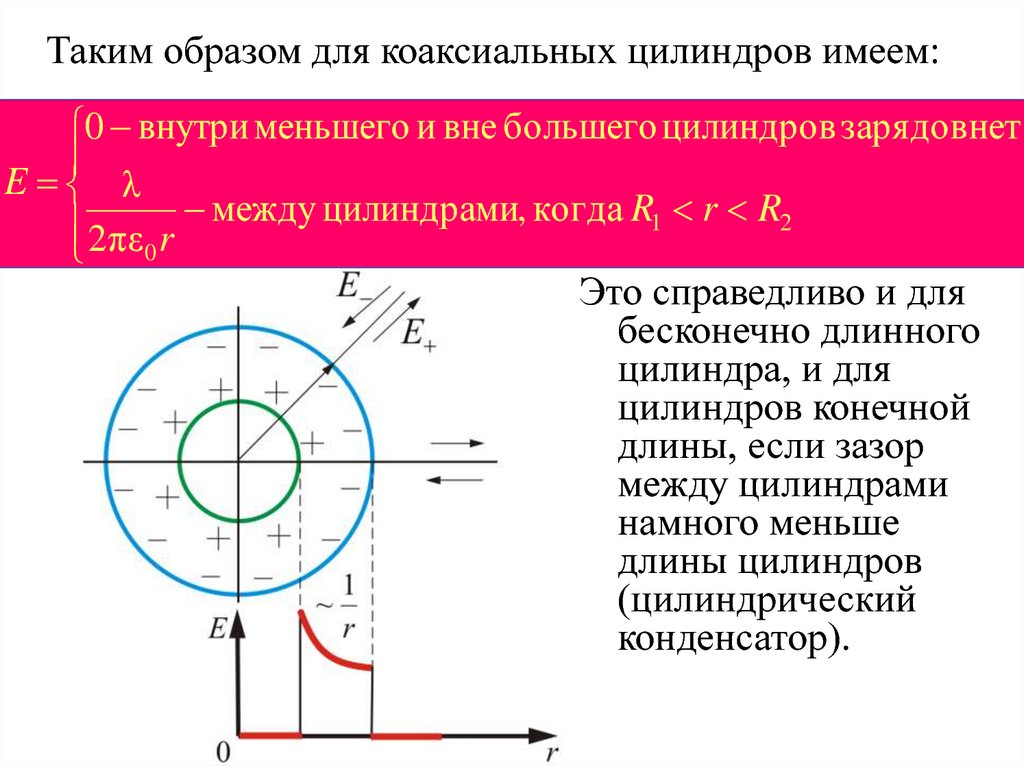
17. Таким образом для коаксиальных цилиндров имеем:

0 внутри меньшего и вне большего цилиндров зарядов нет
E λ
между
цилиндрами
,
когда
R
r
R
1
2
2πε r
0
Это справедливо и для
бесконечно длинного
цилиндра, и для
цилиндров конечной
длины, если зазор
между цилиндрами
намного меньше
длины цилиндров
(цилиндрический
конденсатор).

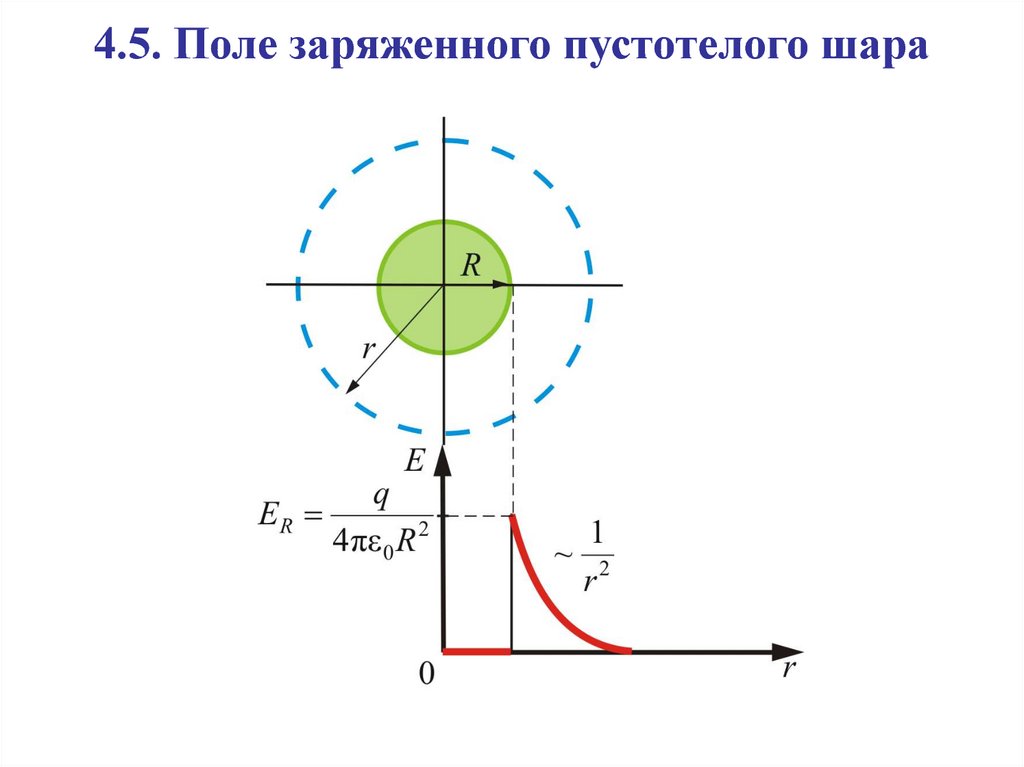
18. 4.5. Поле заряженного пустотелого шара

19.

Вообразим вокруг шара – сферу радиуса r
(рис).

20.

Если r R, то внутрь воображаемой сферы
попадет весь заряд q, распределенный по сфере, тогда
q
ФE E (r ) S Е (r )4πr
ε0
2
откуда поле вне сферы:
q
E (r )
.
2
4πε0r
(4.6)
Внутри сферы, при r R, поле будет равно
нулю, т.к. там нет зарядов:
E (r ) 0.

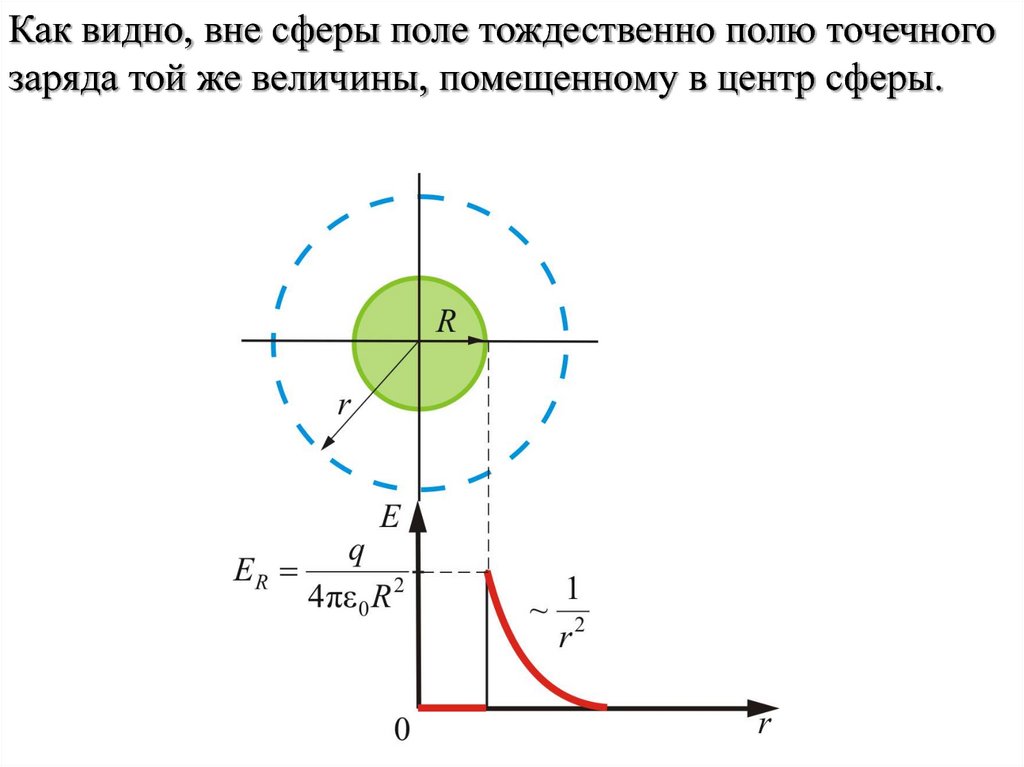
21.

Как видно, вне сферы поле тождественно полю точечного
заряда той же величины, помещенному в центр сферы.

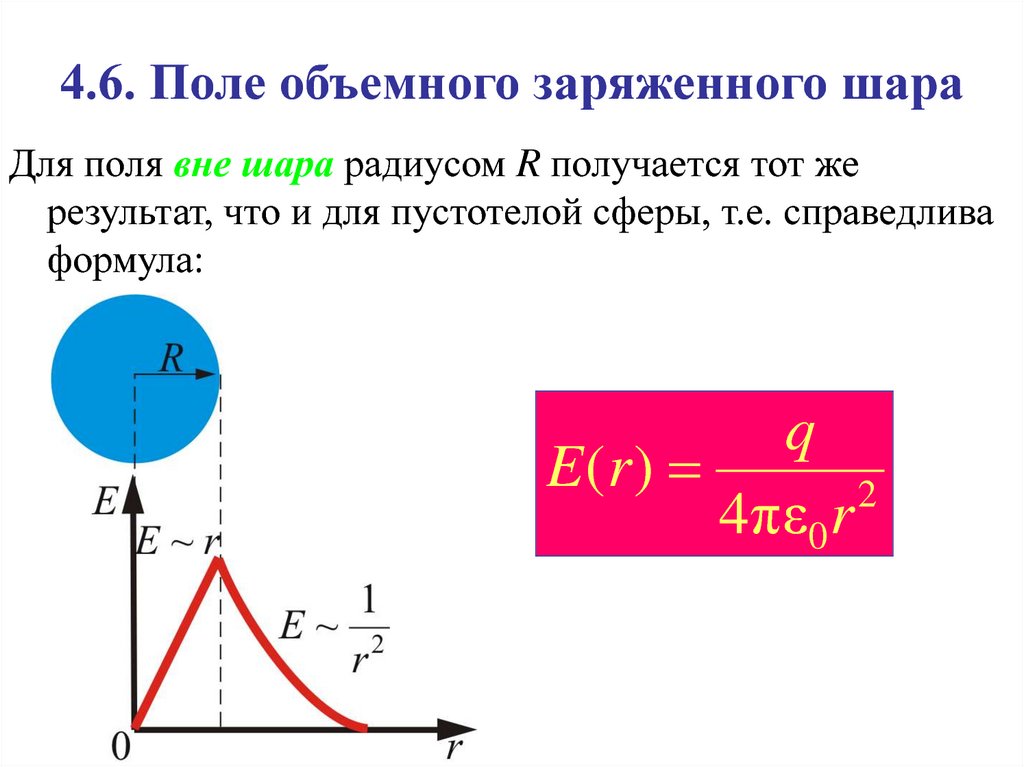
22. 4.6. Поле объемного заряженного шара

Для поля вне шара радиусом R получается тот же
результат, что и для пустотелой сферы, т.е. справедлива
формула:
q
E (r )
2
4πε0 r

23.

Внутри шара при r R, сферическая поверхность
будет содержать в себе заряд, равный
4 3
q ρ πr ,
3
q
,
где ρ – объемная плотность заряда,
V
объем шара -
4
3
V πr
3
Тогда по теореме Остроградского-Гаусса запишем
1 4 3
ФE E (r ) S Е (r ) 4πr ρ πr
ε0 3
2

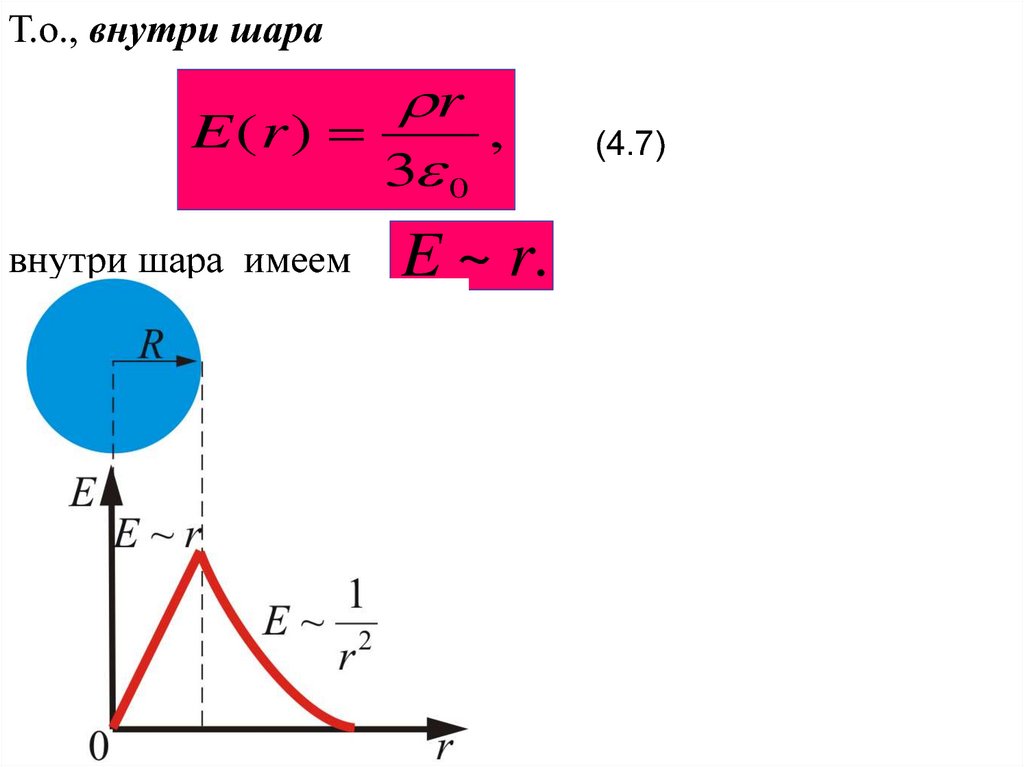
24.

Т.о., внутри шара
r
E (r )
,
3 0
внутри шара имеем
E ~ r.
(4.7)

25. таким образом, имеем: поле объемного заряженного шара

qr
r
4 R 3 3 внутри шара (r R)
0
0
q
E
на поверхности шара (r R)
2
4 0 R
q
вне шара (r R)
2
4 0 r