Многоугольники

1.

2.

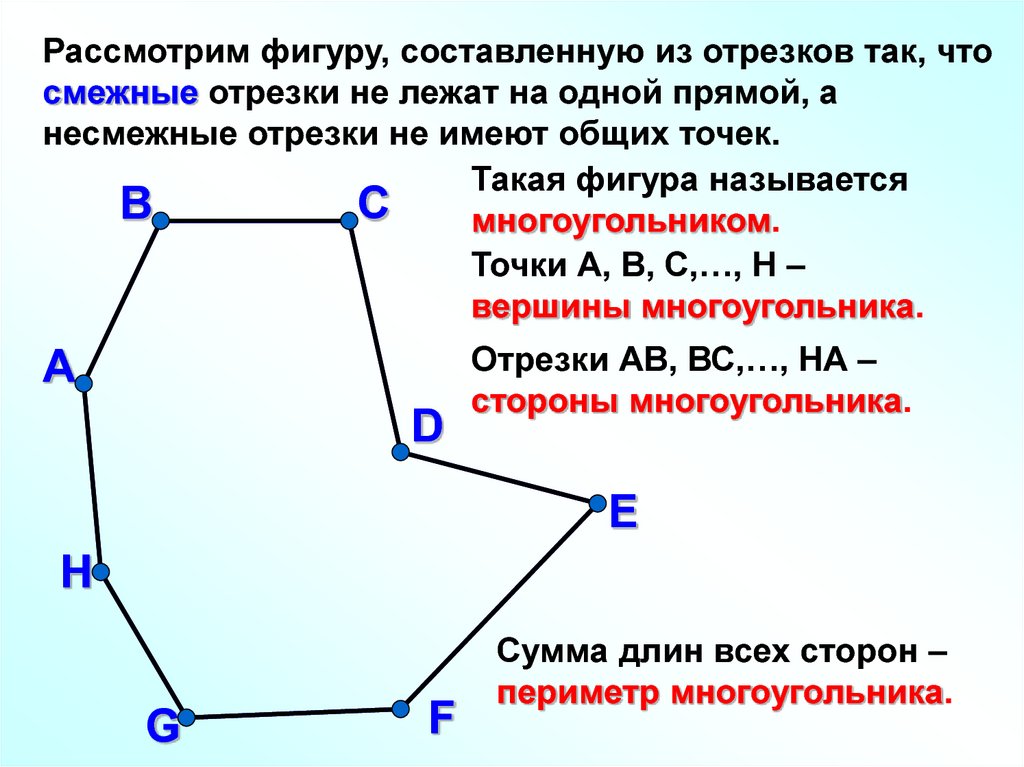
Рассмотрим фигуру, составленную из отрезков так, что
смежные отрезки не лежат на одной прямой, а
несмежные отрезки не имеют общих точек.
Такая фигура называется
В
С
многоугольником.
Точки А, В, С,…, H –
вершины многоугольника.
А
D
Отрезки АВ, ВС,…, HА –
стороны многоугольника.
E
H
G
F
Сумма длин всех сторон –
периметр многоугольника.

3.

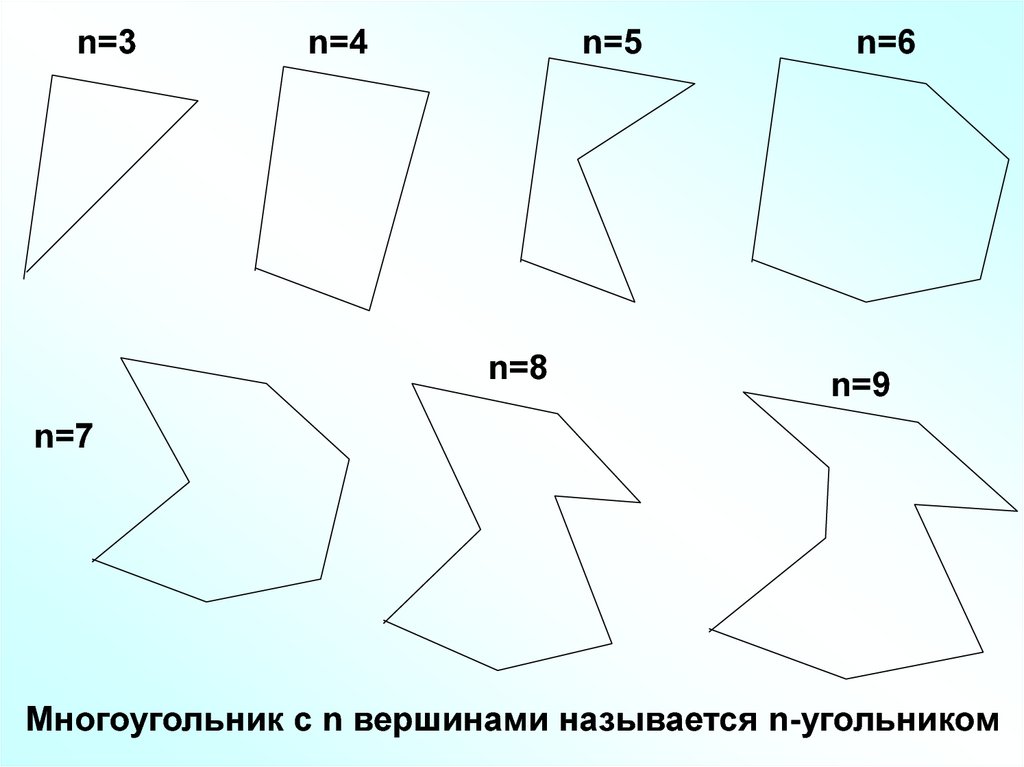
n=3
n=4
n=5
n=8
n=6
n=9
n=7
Многоугольник с n вершинами называется n-угольником

4.

В
С
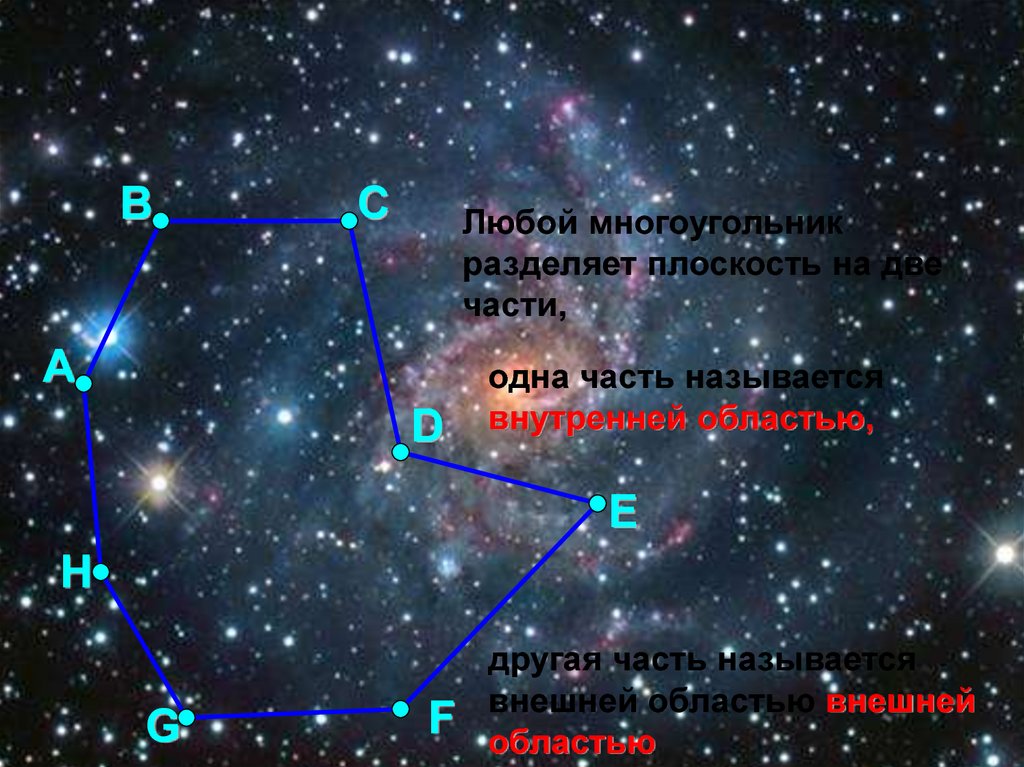
Любой многоугольник
разделяет плоскость на две
части,
А
D
одна часть называется
внутренней областью,
E
H
G
F
другая часть называется
внешней областью внешней
областью

5.

Фигуру, состоящую из многоугольника и его
внутренней области, также называют
многоугольником.
В
А2
С
А1
А3
А
D
А7
E
H
А6
G
F
А5
А4

6.

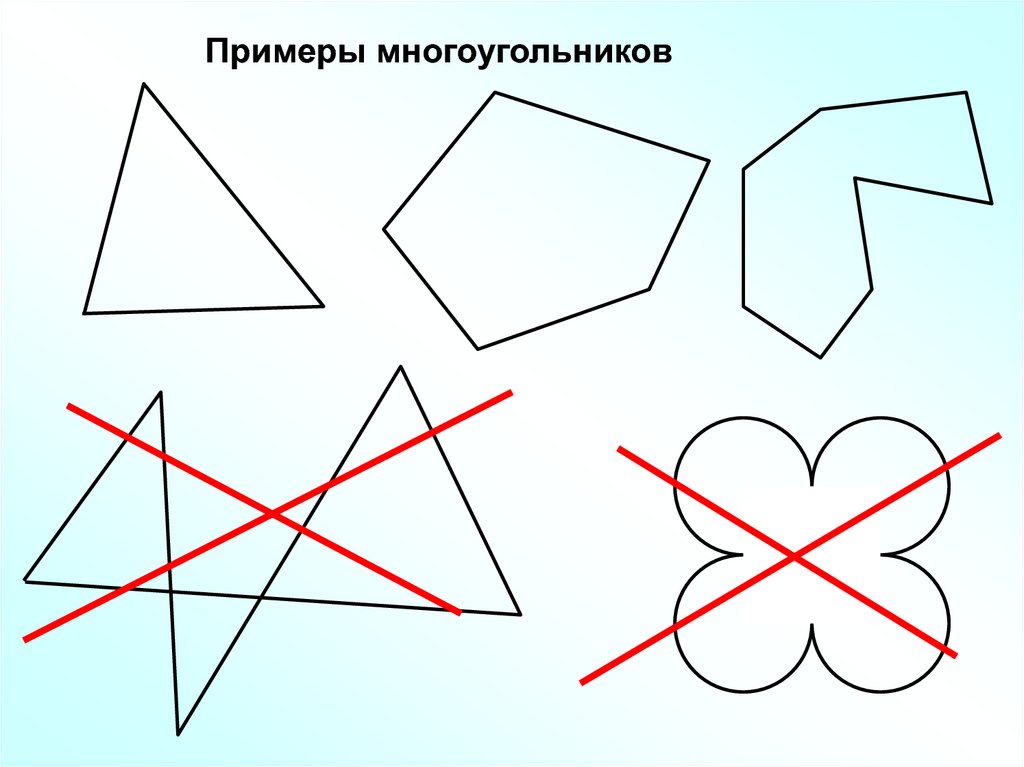
Примеры многоугольников

7.

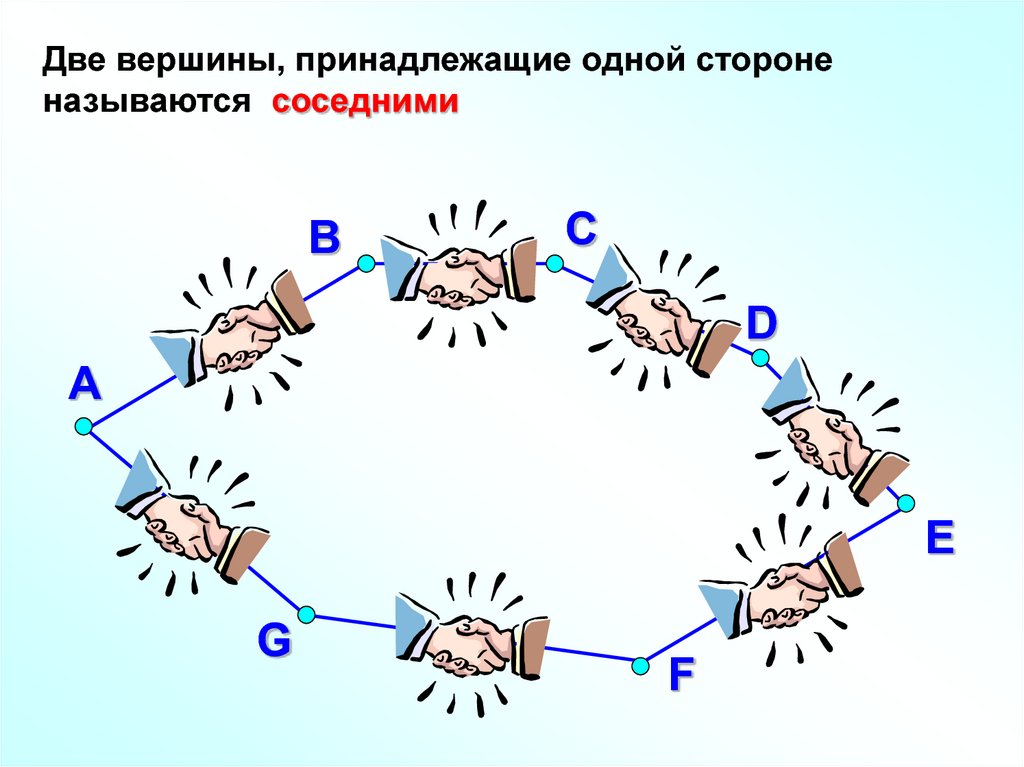
Две вершины, принадлежащие одной стороне
называются соседними
В
С
D
А
E
G
F

8.

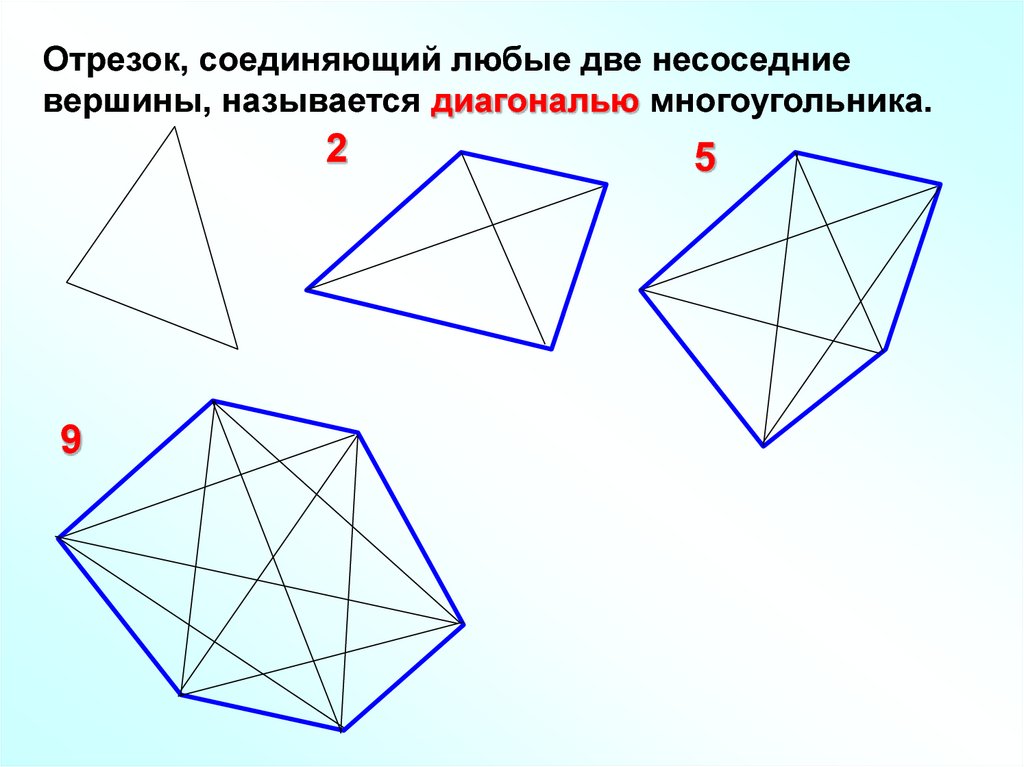
Отрезок, соединяющий любые две несоседние
вершины, называется диагональю многоугольника.
2
9
5

9.

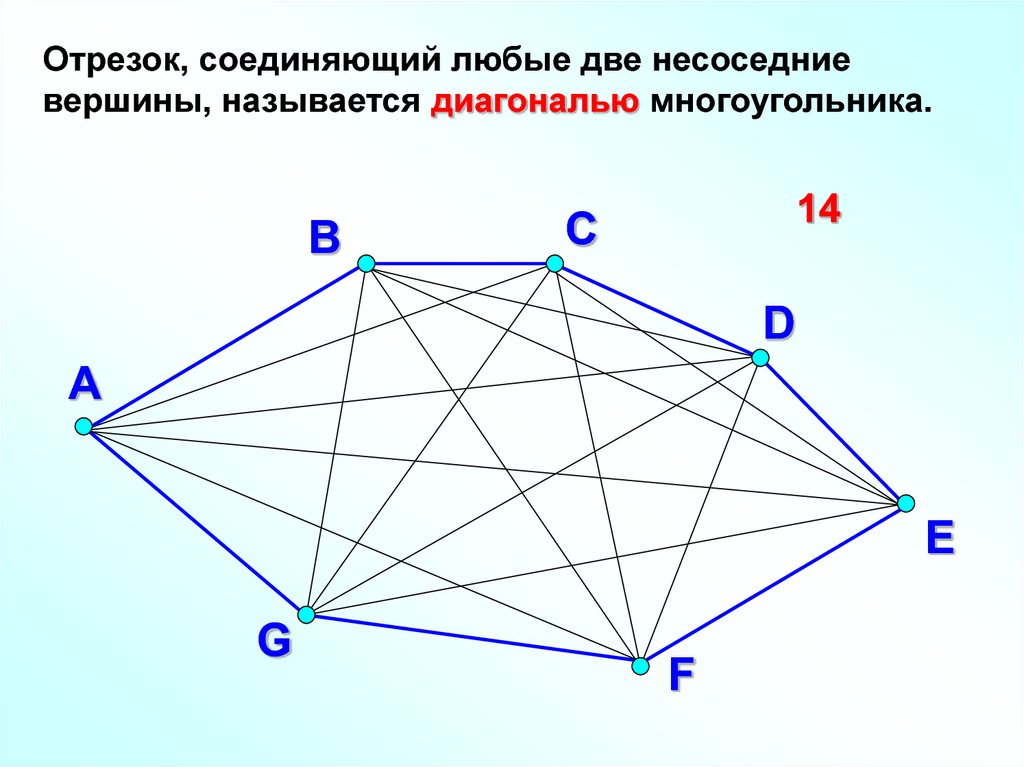
Отрезок, соединяющий любые две несоседние
вершины, называется диагональю многоугольника.
В
14
С
D
А
E
G
F

10.

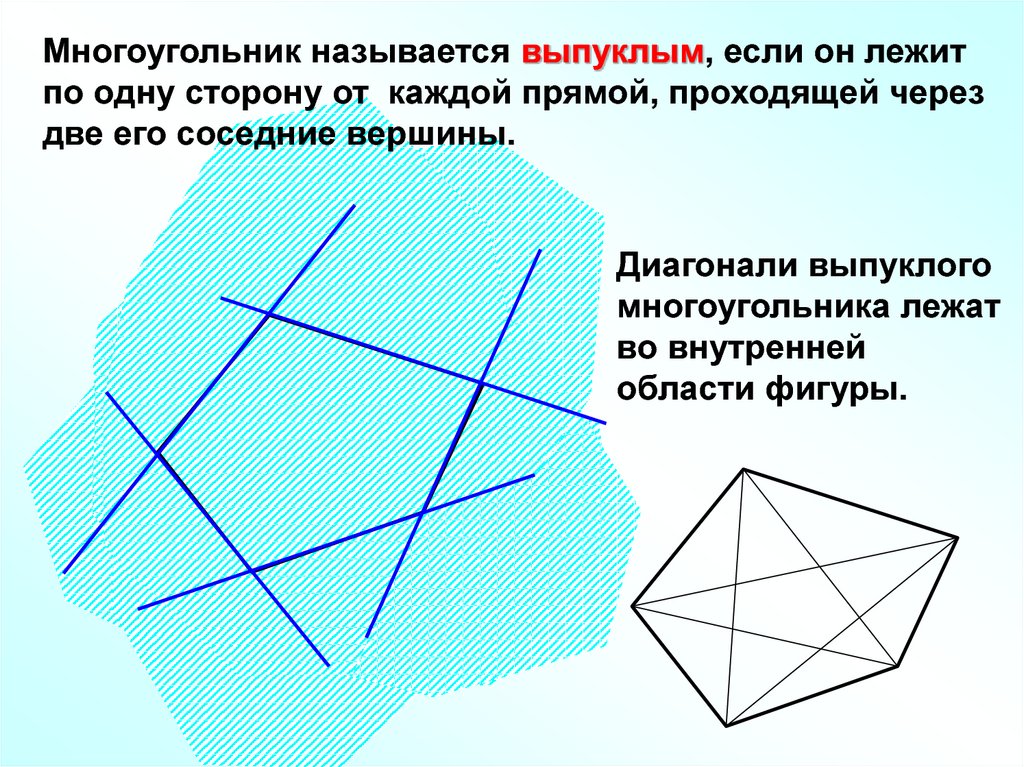
Многоугольник называется выпуклым, если он лежит
по одну сторону от каждой прямой, проходящей через
две его соседние вершины.
Диагонали выпуклого
многоугольника лежат
во внутренней
области фигуры.

11.

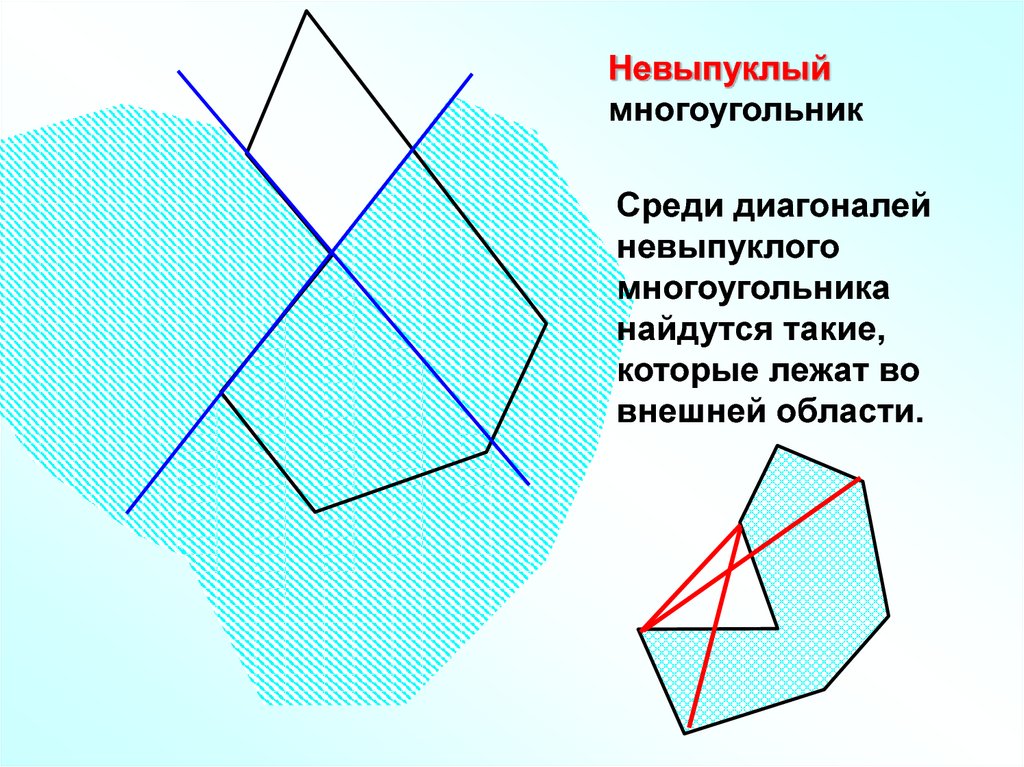
Невыпуклый
многоугольник
Среди диагоналей
невыпуклого
многоугольника
найдутся такие,
которые лежат во
внешней области.

12.

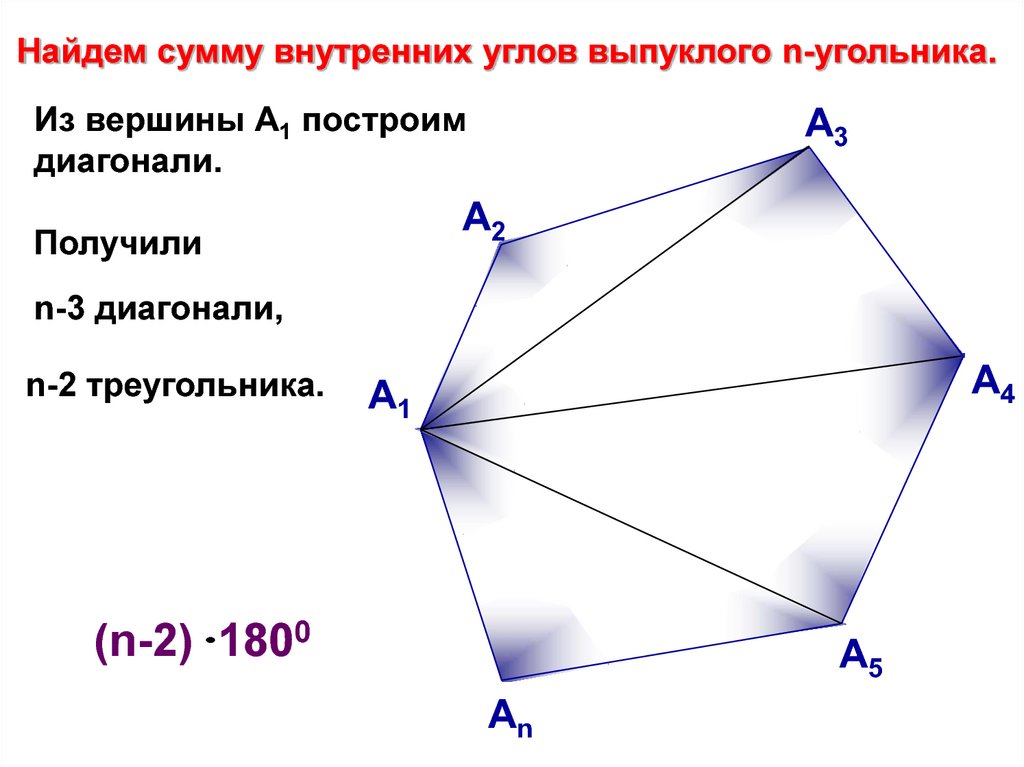
Найдем сумму внутренних углов выпуклого n-угольника.
Из вершины А1 построим
диагонали.
А3
А2
Получили
n-3 диагонали,
n-2 треугольника.
А4
А1
(n-2) 1800
А5
Аn