Численное дифференцирование

1.

Численное дифференцирование
Рассмотрим функцию y=f(x).
По определению производной
f ' ( x ) lim
x 0
f x x f x
x

2.

Численное дифференцирование
Рассмотрим функцию y=f(x).
По определению производной
Из определения предела получаем
приближенное равенство
f ' ( x ) lim
x 0
f'( x)
f x x f x
x
f x x f x
x

3.

Численное дифференцирование
Рассмотрим функцию y=f(x).
По определению производной
f ' ( x ) lim
Из определения предела получаем
приближенное равенство
f'( x)
x 0
f x x f x
x
f x x f x
x
Рассмотрим функцию y=f(x), заданную на интервале [a;b].
Разделим интервал [a;b] на n равных частей.
Занумеруем полученные точки xi начиная с нулевого номера
a=xo<x1< … <xn=b.
Длину каждого интервала будем называть шагом h=(b-a)/n,
а полученные точки {xi } и шаг h разбиением интервала [a;b].

4.

Численное дифференцирование
Рассмотрим функцию y=f(x).
По определению производной
f ' ( x ) lim
Из определения предела получаем
приближенное равенство
f'( x)
x 0
f x x f x
x
f x x f x
x
Рассмотрим функцию y=f(x), заданную на интервале [a;b].
Разделим интервал [a;b] на n равных частей.
Занумеруем полученные точки xi начиная с нулевого номера a=xo<x1< … <xn=b.
Длину каждого интервала будем называть шагом h=(b-a)/n,
а полученные точки {xi } и шаг h разбиением интервала [a;b].
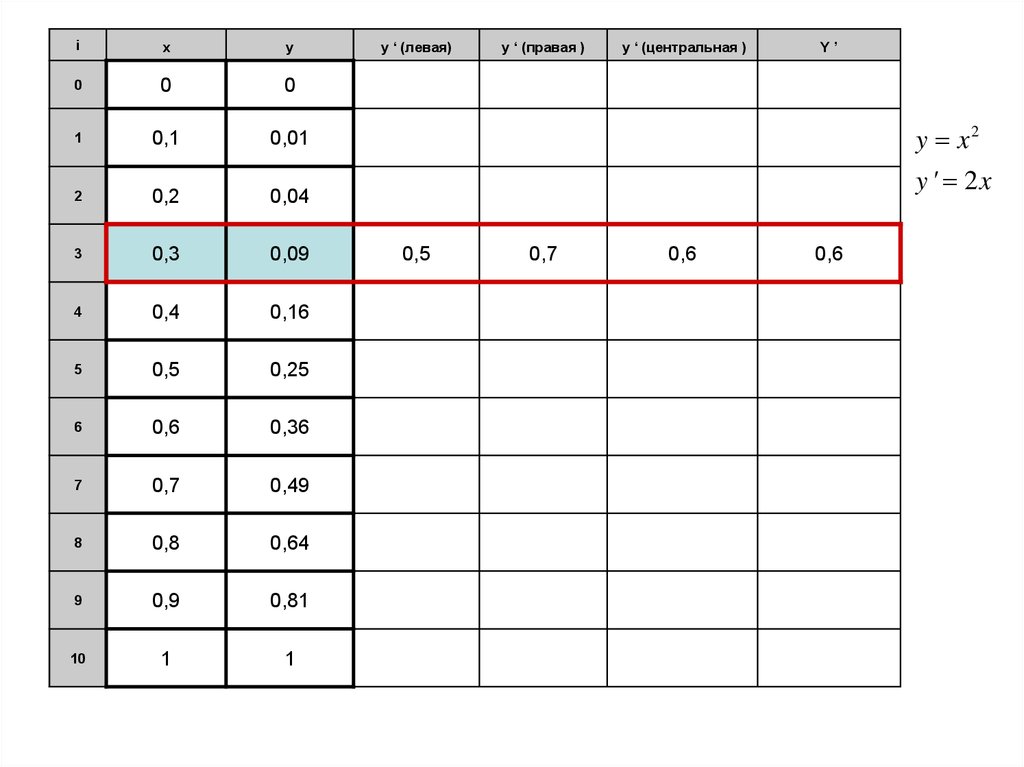
В каждой точке xi вычислим значение функции yi =f(xi ).
Полученную пару (xi ; yi ) будем называть узлами функции.

5.

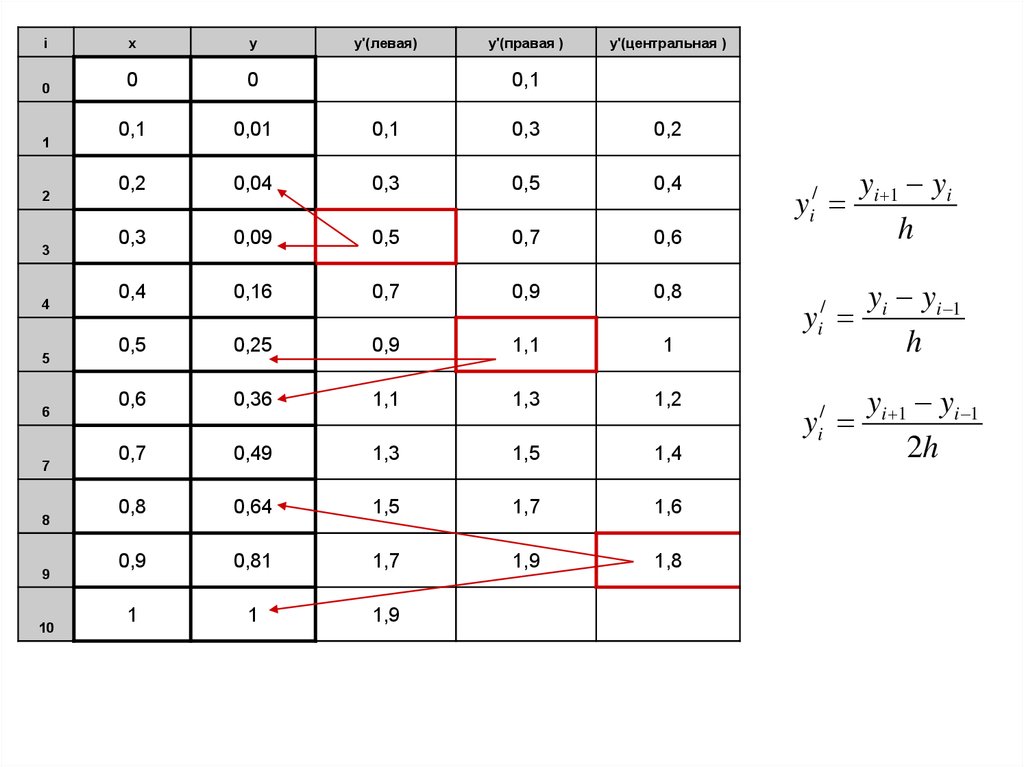
По формуле приближенного значения производной
f'( x)
f x x f x
x
(если возьмем x=