Similar presentations:
Основные уравнения теории оболочек, безмоментная теория оболочек вращения
1. Основные уравнения теории оболочек, безмоментная теория оболочек вращения
Доцент кафедрысамолетостроения
к.т.н. Мухин Д.В.
2.
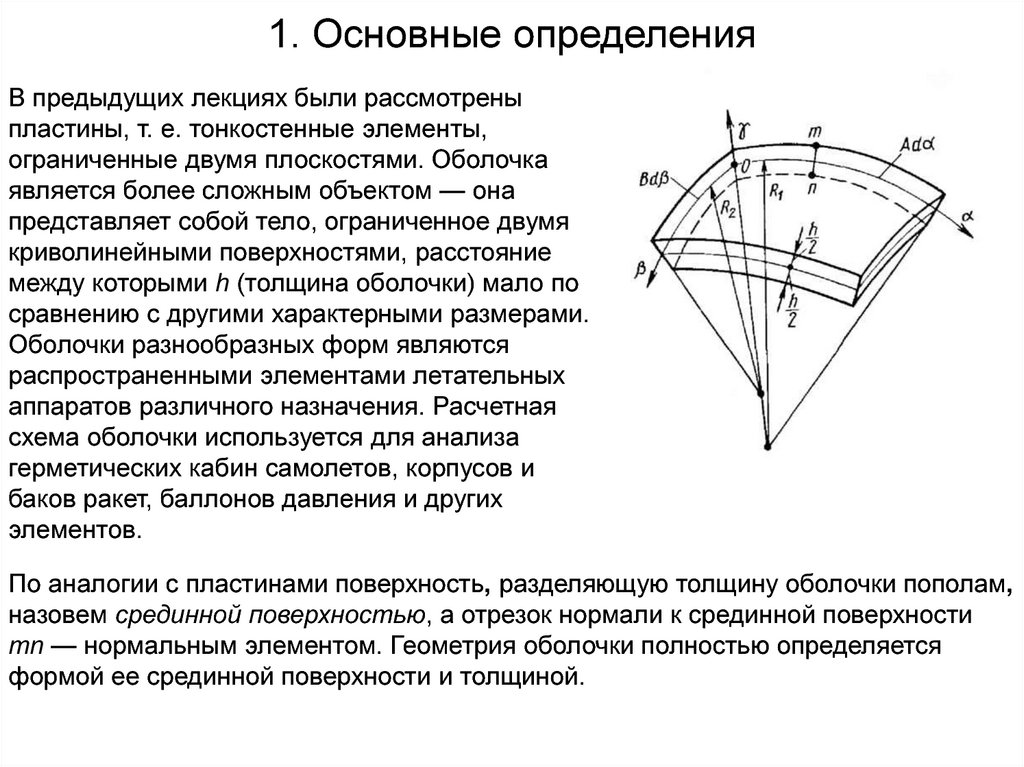
1. Основные определенияВ предыдущих лекциях были рассмотрены
пластины, т. е. тонкостенные элементы,
ограниченные двумя плоскостями. Оболочка
является более сложным объектом — она
представляет собой тело, ограниченное двумя
криволинейными поверхностями, расстояние
между которыми h (толщина оболочки) мало по
сравнению с другими характерными размерами.
Оболочки разнообразных форм являются
распространенными элементами летательных
аппаратов различного назначения. Расчетная
схема оболочки используется для анализа
герметических кабин самолетов, корпусов и
баков ракет, баллонов давления и других
элементов.
По аналогии с пластинами поверхность, разделяющую толщину оболочки пополам,
назовем срединной поверхностью, а отрезок нормали к срединной поверхности
mn — нормальным элементом. Геометрия оболочки полностью определяется
формой ее срединной поверхности и толщиной.
3.
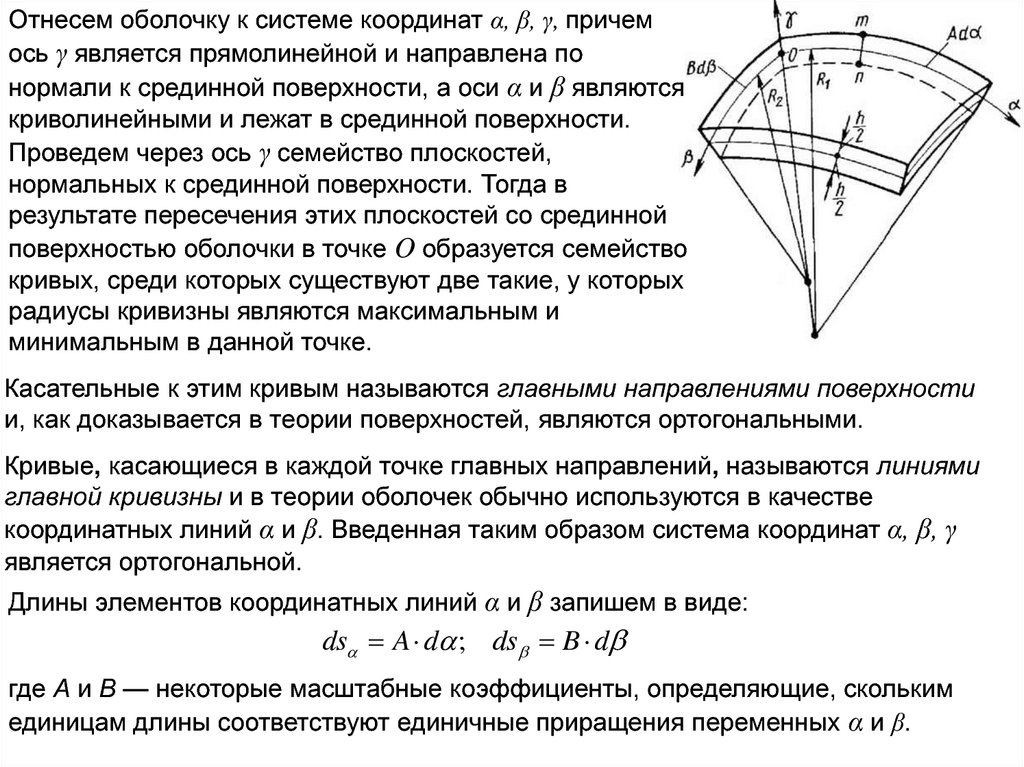
Отнесем оболочку к системе координат α, β, γ, причемось γ является прямолинейной и направлена по
нормали к срединной поверхности, а оси α и β являются
криволинейными и лежат в срединной поверхности.
Проведем через ось γ семейство плоскостей,
нормальных к срединной поверхности. Тогда в
результате пересечения этих плоскостей со срединной
поверхностью оболочки в точке O образуется семейство
кривых, среди которых существуют две такие, у которых
радиусы кривизны являются максимальным и
минимальным в данной точке.
Касательные к этим кривым называются главными направлениями поверхности
и, как доказывается в теории поверхностей, являются ортогональными.
Кривые, касающиеся в каждой точке главных направлений, называются линиями
главной кривизны и в теории оболочек обычно используются в качестве
координатных линий α и β. Введенная таким образом система координат α, β, γ
является ортогональной.
Длины элементов координатных линий α и β запишем в виде:
ds A d ; ds B d
где А и В — некоторые масштабные коэффициенты, определяющие, скольким
единицам длины соответствуют единичные приращения переменных α и β.
4.
Тогда квадрат длины дуги произвольного элемента, лежащего в срединнойповерхности, равен:
ds 2 ds 2 ds 2 A2 d 2 B 2 d 2
Полученное соотношение называется первой квадратичной формой поверхности,
а параметры А и В — коэффициентами первой квадратичной формы.
Для плоскости, отнесенной к декартовым координатам х,y получим
ds 2 dx 2 dy 2
т. е. А=В=1,
Для плоскости, отнесенной к полярным координатам r, θ
ds 2 dr 2 r d 2
т. е. А=1 В=r
Геометрия срединной поверхности оболочки полностью определяется
коэффициентами А, В и главными радиусами кривизны R1, R2, которые в общем
случае являются функциями переменных α и β.
Для элемента длины дуги произвольной линии, заключенной между поверхностями
на расстоянии γ от срединной поверхности можно записать следующую формулу:
2
2
2
2
ds A 1 d B 1 d 2 d 2
R1
R2
2
2
5.
Однако для оболочек небольшой кривизны, у которых радиусы кривизнысущественно больше толщины оболочки дроби в скобках оказываются
существенно меньше единицы и ими можно пренебречь, формула упрощается:
ds 2 A2 d 2 B 2 d 2 d 2
6.
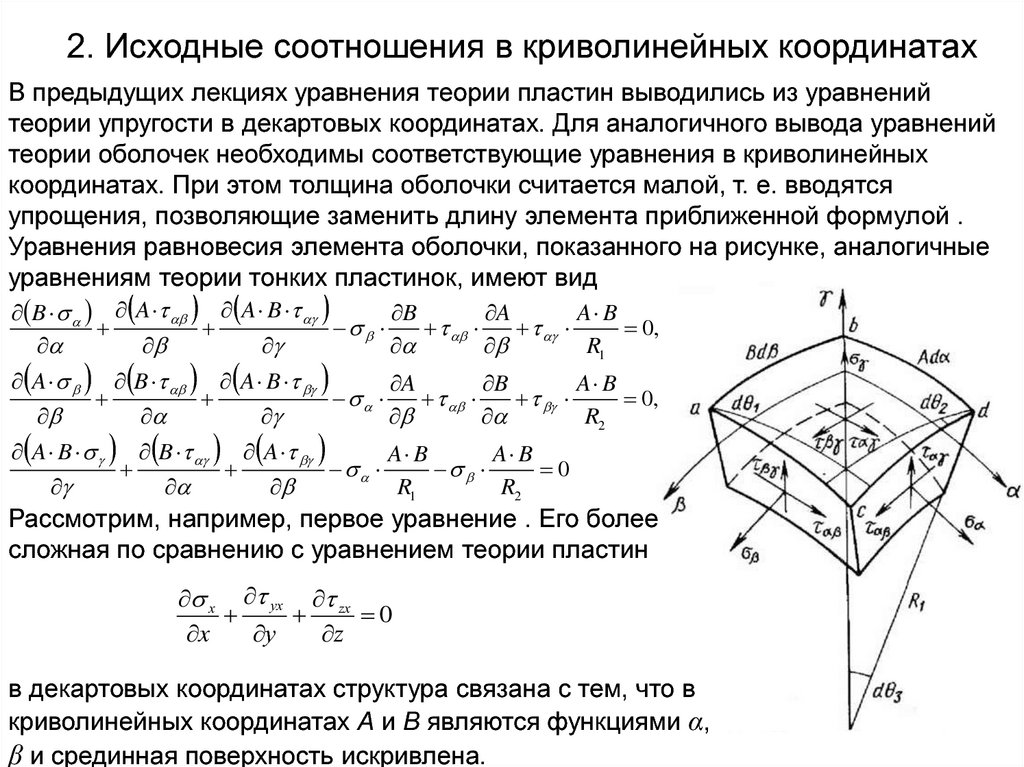
2. Исходные соотношения в криволинейных координатахВ предыдущих лекциях уравнения теории пластин выводились из уравнений
теории упругости в декартовых координатах. Для аналогичного вывода уравнений
теории оболочек необходимы соответствующие уравнения в криволинейных
координатах. При этом толщина оболочки считается малой, т. е. вводятся
упрощения, позволяющие заменить длину элемента приближенной формулой .
Уравнения равновесия элемента оболочки, показанного на рисунке, аналогичные
уравнениям теории тонких пластинок, имеют вид
B A A B
B
A
A B
0,
R1
A B A B
A
B
A B
0,
R2
A B B A
A B
A B
0
R1
R2
Рассмотрим, например, первое уравнение . Его более
сложная по сравнению с уравнением теории пластин
х ух zх
0
x
у
z
в декартовых координатах структура связана с тем, что в
криволинейных координатах А и В являются функциями α,
β и срединная поверхность искривлена.
7.
В результате, если bd A d , ab B dто в силу искривления поверхности
A
B
d , cd ab
d
и за счет углов dθ1, dθ2 и dθ3 усилия определяемые
напряжениями σβ, ταβ и ταγ дают проекции на
направление α.
ac bd
Более сложными, чем соотношения в теории пластин,
являются и геометрические соотношения:
u A u
u 1 u u
1 u
,
,
A A B R1
A R1
u 1 u u
u B u
1 u
,
,
B A B R2
B R2
u
,
u
1 u 1 u
A u B
B A A B A B
Здесь — uα, uβ, uγ перемещения по направлениям α, β, γ.
8.
Физические соотношения выражают закон Гука и с точностью до обозначенийсовпадают с аналогичными уравнениями теории пластин
1
, 2 1 ,
E
E
1
2 1
,
,
E
E
1
2 1
,
.
E
E
Здесь учтено, что G
2 1
E
9.
3. Основные соотношения общей теории оболочекТеория оболочек, так же как и теория пластин,
базируется на гипотезах Кирхгофа для нормального
элемента mn. Согласно этим гипотезам следует
принять
0
и из геометрических соотношений при γ<<R1,2
получим
uγ=w(α,β) и линейное распределение
перемещений uα и uβ по толщине оболочки,
аналогичное теории пластинок
u u , u v
где
u(α,β), v(α,β), w(α,β) — перемещения срединной поверхности в направлениях α, β
и прогиб оболочки,
u 1 w
v 1 w
,
R1 A
R2 B
- углы поворота
поверхности.
нормали
к
срединной
10.
Определение линейных и угловых деформацийПодставляя полученные выражения для перемещений в геометрические
соотношения, получим выражения для деформаций
0
0 , 0 ,
где
0
1 u
v A w
,
A A B R1
1 v
u B w
,
B A B R2
0
0
-деформации удлинения
и сдвига срединной
поверхности;
1 u 1 v
u A
v B
B A A B A B
1
1 A
,
A A B
- изменения кривизны и кручение
срединной
поверхности
1
1 B
,
B
A B
A B
1 1
B A A B A B
11.
Определение напряженийВ соответствии с гипотезами Кирхгофа в
законе
Гука
следует
пренебречь
напряжениями σγ по сравнению с σα и σβ.
Выражая из закона Гука напряжения и
подставляя
в
полученные
равенства
выражения для деформаций, получаем:
E 0 0 , E 0 0 ,
0
E 1
1
2
где
E
E
1 2
Так же, как и в теории пластин, напряжения линейно изменяются по толщине
оболочки.
12.
Погонные усилия и моментыПо аналогии с теорией пластин вводим
понятие погонных усилий и моментов.
Учитывая связь погонных усилий и
моментов с действующими напряжениями,
рассмотренную в теме пластин и заменяя
обозначения осей получаем:
h
2
N d ,
h
2
h
2
Q d ,
h
2
h
2
M d ,
h
2
h
2
N d ,
h
2
h
2
N d ,
h
2
h
2
Q d
h
2
h
2
M d ,
h
2
h
2
M d ,
h
2
13.
Таким образом, в качестве основногоэлемента оболочки можно рассматривать
элемент
срединной
поверхности,
нагруженный усилиями и моментами,
показанными на рисунке. Подставляя
напряжения в соотношения для погонных
усилий, получим
h
0
E 1
,
2
D
1
2
N E h 0 0 ,
N E h 0 0 ,
N
M D ,
M D ,
M
где
E h3
D
12 1 2
- изгибная или цилиндрическая жесткость оболочки
Усилия и моменты должны быть связаны уравнениями равновесия, которые
могут быть получены непосредственно из рассмотрения равновесия элемента,
показанного на рисунке
14.
Поставляя усилия в уравнения равновесия получим:B N A N
B
A A B
N
N
Q A B q 0,
R
1
A N B N
A
B A B
N
N
Q A B q 0,
R2
B Q A Q
A B
A B
N
N
A B q 0,
R1
R2
B M A M
B
A
M
M
A B Q 0,
A M B M
A
B
M
M
A B Q 0.
Уравнения
сил
Уравнения
моментов
где qα, qβ, qγ - поверхностные нагрузки, отнесенные к срединной поверхности
оболочки
Полученные соотношения представляют собой исходную систему 19-ти
уравнений общей теории оболочек, которые включают девятнадцать неизвестных
функций переменных α, β: восемь усилий и моментов Nα, Nβ, Nαβ, Qα, Qβ, восемь
0
0
0
компонентов деформаций — , , , , , , , и три перемещения u, v, w.
При А=B=1 и α=х, β=y полученные уравнения преобразуются в уравнения теории
пластин, рассмотренные ранее.
15.
Согласно общей схеме решения задачи в перемещениях, система уравненийтеории оболочек может быть сведена к трем уравнениям относительно
перемещений и, и, w. Для этого необходимо из двух уравнений моментов выразить
перерезывающие силы
1 B M A M
B
A
M
M ,
A B
1 A M B M
A
B
Q
M
M
.
A B
Q
и подставить их в три уравнения сил. Выражая далее в полученных таким образом
трех уравнениях усилия и моменты через перемещения, можно записать
следующую систему:
L1u u L1v v L1w w q ,
L2u u L2 v v L2 w w q ,
L u L v L w q .
3v
3w
3u
Дифференциальные операторы Lij в общем случае имеют восьмой порядок
дифференцирования и весьма громоздкую форму и здесь не приводятся.
16.
Еслив
результате решения данной системы найдены перемещения
u(α,β), v(α,β), w(α,β), то далее по формулам основных соотношений общей теории
оболочек можно определить компоненты деформации, и с помощью соотношений
связывающих деформации и погонные усилия и моменты — усилия и моменты.
Напряжения в оболочке определяются равенствами, аналогичными теории
пластин
N 12 M
N 12 M
N
12 M
,
,
,
3
3
3
h
h
h
h
h
h
6 Q 2 h 2
6 Q 2 h 2
3 ,
3 ;
h
4
h
4
Данные формулы соответствуют наиболее распространенному случаю, когда на
поверхностях оболочки отсутствуют касательные составляющие внешней нагрузки.
17.
4.Граничные условияРазрешающие уравнения общей теории оболочек имеют в совокупности восьмой
порядок по переменным α и β. В каждой точке края оболочки необходимо записать
четыре граничных условия. Так, на крае оболочки α=const в общем случае должны
быть заданы четыре граничных условия:
u или Nα, v или Nαβ, w или Q*α, ϑα или Mα
В более общем случае (упругое закрепление) может быть задана линейная
комбинация двух функций:
u k1 N , v k2 N , w k3 Q * , k4 M
На защемленном крае к условиям отсутствия прогиба и угла поворота
необходимо добавить условия отсутствия тангенциальных перемещений
срединной поверхности, т. е.
const u v w 0
при const u v w 0
при
Здесь углы поворота нормали к срединной поверхности ϑA и ϑВ определяются
ранее полученными равенствами
u 1 w
v 1 w
,
R1 A
R2 B
18.
Распространенным является так называемое скользящее шарнирное опирание(свободное опирание) края. Граничные условия при этом имеют вид:
const
v w 0, M N 0,
при const
u w 0, M N 0.
при
Согласно данным зависимостям, например, край α=const может свободно
перемещаться в направлении α (Nα=0) и закреплен от перемещений в
направлении β (v=0). Если отсутствуют все тангенциальные перемещения, то
условия Να=0 и Νβ=0 следует заменить соответственно на и=0 и v=0. Если же
край свободен в отношении тангенциальных перемещений, условия v=0 и и=0
заменяются на Nαβ=0 при α=const и β=const.
К условиям на свободном крае пластины необходимо добавить условия
отсутствия тангенциальных усилий, т. е.:
const
N N M Q * 0,
при const
N N M Q * 0.
при
*
*
Здесь Q и Q — обобщенные перерезывающие силы, которые определяются
равенствами, аналогичными теории пластин, т. е.
1 M
Q Q
,
B
*
1 M
Q Q
A
*
Qα и Qβ выражаются через моменты ранее полученными соотношениями.
19.
5. Полная энергия оболочкиПотенциальная энергия тонкой
аналогичный теории пластин:
оболочки небольшой кривизны, имеет вид,
h2
1
U d A B d d
2 h
2
Подставляя деформации с помощью полученных ранее равенств и учитывая
выражения для усилий и моментов, получим:
U
1
0
0
0
N
N
N
M M M A B d d
2
Вариация работы внешних сил имеет вид
A q u q v q w A B d d
Полная энергия оболочки определяется общей формулой Э=U - А.
Согласно принципу Лагранжа
Э U A
20.
6. Осесимметричная деформация цилиндрической оболочкиРассмотрим достаточно простой и тем не менее важный для приложений пример
— на задачу об осесимметричном изгибе цилиндрической оболочки. Полученные
результаты позволят также сделать некоторые важные выводы, которые будут
использованы в дальнейшем.
Пусть тонкая круговая цилиндрическая оболочка постоянной толщины h
нагружается нормальной нагрузкой (давлением qγ=p(α)) и касательной нагрузкой
qα=q(α). Если действующие на торцах оболочки силы также не зависят от окружной
координаты β, то как нагружение, так и напряженно-деформированное состояние
оболочки будут осесимметричными. При этом v=0, а перемещения u, w и все
усилия и моменты будут завиcеть только от осевой координаты α.
Согласно
рисунку
цилиндрической СК
в
принятой
ds 2 d 2 R d 2
т. е. А=1, В=R.
Кроме того, очевидно, что R1=∞ и R2=R.
21.
Геометрические соотношения типа в цилиндрическихосесимметричной задачи преобразуются к виду:
координатах
для
u A u 1 u u 1 u
u
1 u
,
A A B R1 1 1 R
u B u
1 u
1 u u R u u
,
B A B R2 R 1 R R R
u
,
u 1 u u u 1 u u u u
,
A R1 1
1 u u
0,
B R2
u
u
1 u 1 u
A u B
0
B A A B A B
Две последних
деформации равны
нулю по условию
симметричности
То есть, подводя итоги:
u
u
u
u u
, ,
,
,
R
Совпадает с зависимостями
Сопротивления материалов
22.
На основании гипотез Кирхгофа получим частную форму выражений дляперемещений для рассматриваемого случая
u w , u u , w
где w(α) и и(α) — функция прогиба и осевое перемещение точек срединной
поверхности, а ( )' обозначает производную по α.
Подставляя данные выражения в геометрические соотношения имеем
u
u ( ) 0 ,
u
w
0 ,
R R
где
0 u ( ), w , 0
w
.
R
Закон Гука (относительно напряжений) принимает вид:
E 0 0 ,
E 0 0 .
где E
E
1 2
Подставляем в закон Гука выражения для 0 , 0 , и находим усилия и моменты,
выражая их через напряжения
23.
h2N
w
R
d E u ,
h 2
h2
w
N d E u ,
R
h 2
h2
M
d D w ,
h 2
h2
M
d D w ,
h 2
здесь, как и ранее: E E 1 2 , D E h 3 12
24.
Выведем теперь уравнения равновесия.Выделим из оболочки элемент, показанный
на рисунке. б и приравняем нулю сумму
всех
сил,
действующих
в
осевом
направлении α, сумму проекций сил на
нормаль к поверхности и сумму моментов
относительно
элемента
параллели
(остальные
уравнения
равновесия
удовлетворяются тождественно). Получим:
N q 0,
Q
N
R
p 0,
M Q 0
Полученные соотношения представляют собой систему основных уравнений для
осесимметрично нагруженной цилиндрической оболочки. Семь полученных
уравнений включают столько же неизвестных — два перемещения и, w и пять
усилий и моментов Nα, Nβ, Qα, Mα, Mβ. Как отмечалось ранее, эту систему можно
свести к уравнениям, включающим в качестве неизвестных перемещения.
Из последнего уравнения и выражений для погонных нагрузок получаем:
Q M D w
Подставляем в первые два уравнения из последней группы выражения погоных
нагрузок
q
1
w h 2 IV
p
u w
,
u w
R
E h
R
R 12
E h
25.
Во многих случаях задача является статически определимой относительноусилий Να — они могут быть получены путем интегрирования уравнения,
N q 0
причем произвольная постоянная определяется по известному значению Να = N
на каком-либо торце оболочки. В этих случаях вместо двух уравнений можно
получить одно уравнение относительно прогиба w.
Пусть на оболочку действует только
внутреннее давление р. При q=0 из
первого уравнения получим Nα=N (если
р=const, то N 0,5 p R
). Исключая из
формул и’ найдем
E h
N
w N
R
В этом случае второе уравнение после подстановки выражений для Qα и Νβ
E h
N
примет вид:
D w IV 2 w p
R
R
1
N
или w IV 4 k 4 w p
D
R
E h
3 1 2
4
k
где
4 R2 D
R2 h2
26.
Краевой эффект и безмоментное состояниеОбщее решение дифференциального уравнения запишем в виде:
w e k C1 cos k C2 sin k e k C3 cos k C4 sin k w0
где w0(α) — частное решение неоднородного уравнения, зависящее от вида
правой части. Четыре произвольных постоянных C1,С2,С3,С4 определяются из
четырех граничных условий при α=0 и α=l.
Если оболочка рассматривается как полубесконечная (l→∞), то из условия
ограниченности решения при α→∞ следует положить С2 = С3 = 0. Тогда
w e k C1 cos k C2 sin k w0
Здесь константы С1 и С2 определяются из граничных условий на краю α=0; они
характеризуют быстро затухающее решение типа краевого эффекта,
описывающее местный изгиб оболочки вблизи края α=0. Так как eπ≈0,043, то
влиянием краевого эффекта практически можно пренебречь при α≥π·k или, если
положить μ≈0,3, при 2,5 R h . Например при R/h =100 и R/h =400 ширина
зоны краевого эффекта равна 0,25R и 0,125R соответственно.
Если длинa оболочки превышает ширину зоны краевого эффекта ( l 2,5 R h ), то
такую оболочку можно считать длинной и изгиб вблизи каждого из двух краев и
можно рассматривать независимо друг от друга, используя решение для
полубесконечной оболочки (при этом в каждом случае координата α
отсчитывается от рассматриваемого края в направлении другого края).
27.
,Если правая часть дифференциального уравнения представлена в виде полинома
по степеням α с показателями, не превышающими трех, то частное решение имеет
вид:
2
w0
R
N
p
E h
R
В более общем случае, если правая часть ДУ меняется достаточно плавно, данное
выражение может быть использовано как приближенное частное решение.
Полученное частное может быть также получено как решение ДУ при D=0.
Из равенств и соотношений, определяющих распределение напряжений по
толщине оболочки, следует, что при D=0, Mα=Mβ=Qα=0 и σα=Nα/h, σβ=Nβ/h
т. е. напряжения равномерно распределены по толщине. Такое напряженное
состояние оболочки называется безмоментным и соответственно частное
решение называется безмоментным решением.
Таким образом, можно считать, что общее решение задачи при осесимметричной
деформации тонкой достаточно длинной цилиндрической оболочки складывается
из безмоментного решения w0 и решения краевого эффекта wk.
28.
Краевой эффект возникает в том случае, когда на краю оболочка нагружаетсямоментным образом (поперечными силами, моментами), соединяется с другой
оболочкой шпангоутом и т. п. или закрепляется в отношении поперечного
перемещения w и угла поворота θα. Угол поворота нормали, изгибающие моменты
и перерезывающая сила согласно формулам имеют вид:
w k e k C1 cos k sin k C2 cos k sin k ,
M D w 2 D k 2 e k C1 sin k C2 cos k ,
M M ,
Q D w 2 D k 3 e k C1 cos k sin k C2 cos k sin k
Определим постоянные С1 и С2
для различных типов граничных
условий.
Для защемленного края (см.
рис. б) при α=0 следует принять:
w 0
при этом С1=С2=-w0
w w0 1 e k cos k sin k
29.
Если на торце оболочка закрепленашарнирно (рис. в), то
0 w M 0
получаем
C1 w0 , C2 0
решение имеет вид:
w w0 1 e k cos k .
Из полученных равенств следует, что при увеличении α прогиб приближается к
безмоментной составляющей, т. е. на достаточном удалении от края w=w0
Если оболочка не закреплена в отношении радиального перемещения w и угла
поворота ϑα, то при α=0 Mα=Qα=0 и следовательно С1=С2=0 и w=-w0 т. е. при
таком закреплении краевой эффект отсутствует и прогиб полностью определяется
безмоментным решением.
Таким образом, достаточно длинная цилиндрическая оболочка почти всюду (за
исключением быть может узких участков вблизи краев) находится в безмоментном
состоянии, а в окрестности краев при соответствующих граничных условиях
реализуется локальное изгибное состояние — краевой эффект. Эта особенность
напряженного состояния характерна не только для цилиндрической, но и для
более широкого класса оболочек и позволяет в ряде случаев значительно
упростить расчет.


























 mechanics
mechanics








