Пологие оболочки. Полубезмоментная теория цилиндрических оболочек

1. Пологие оболочки Полубезмоментная теория цилиндрических оболочек

2.

ТЕОРИЯ ПОЛОГИХ ОБОЛОЧЕК
Основные гипотезы и исходные соотношения
Пологой будем называть оболочку, на
поверхности которой можно ввести
некоторую систему криволинейных координат, такую, что расстояние между двумя точками и угол между двумя направлениями на поверхности можно приближенно отождествить с расстояниями
между точками и углами между линиями,
лежащими на некоторой плоскости.
Типичная форма пологой оболочки или искривленной панели показана на рис.а.
Криволинейный элемент abcd поверхности такой оболочки в координатах х, у
можно приближенно отождествить с его проекцией на плоскость ABCD, а
криволинейные координаты х, у — с декартовыми координатами.
Основное упрощение, вытекающее из этого предположения заключается в том, что
метрическое соотношение ds 2 A2 d 2 B 2 d 2 общей теории в координатах х, у
можно приближенно заменить следующим: ds 2 dx 2 dy 2 , т. е. принять А=В=1.
Помимо этого, в теории пологих оболочек принимается, что при проектировании
действующих на элемент сил на оси х и у можно в силу малой кривизны оболочки
не учитывать составляющие от перерезывающих сил Qx и Qy (см. рис. б), а в
геометрических соотношениях, определяющих изменения кривизн, учитывать
только нормальное перемещение w.

3.

В результате уравнения общей теории оболочек упрощаются следующим образом
Уравнения равновесия принимают вид
N x N xy
q x 0,
x
y
M x M xy
Qx 0,
x
y
N xy
x
N y
y
M xy
x
q y 0,
M y
y
Qx Qy N x N y
p 0,
x
y
R1 R2
Qy 0.
Соотношения упругости сохраняются без изменения:
h
N x E h x0 y0 , N y E h y0 x0 , N xy E 1 xy ,
2
D
M x D x y , M y D y x , M xy 1 xy ,
2
Геометрические соотношения записываются в форме
x0
u w
v w
u v
, y0
, xy
,
x R1
y R2
y x
y
x
x y
x
, y
, xy
,
x
y
y
x
где
x
w
w
, y
x
y
Полученные уравнения отличаются от соответствующих уравнений теории пластин
наличием членов Nx/Rl, Ny/R2 во втором уравнении равновесия и членов w/R1, w/R2 в
геометрических соотношениях для линейных деформаций.

4.

Соответственно упрощаются и выражения для перерезывающих сил. Из двух
последних уравнений равновесия имеем
Qx
M y M xy
M x M xy
, Qy
.
x
y
y
x
Обобщенные перерезывающие силы, используемые для записи граничных
условий имеют вид
Qx* Qx
M xy
y
, Q *y Q y
M xy
x
.
С учетом приведенных зависимостей граничные условия записываются в той же
форме как и в общей теории оболочек.
Полученные уравнения в силу своей простоты по сравнению с уравнениями общей
теории широко применяются для решения самых разнообразных задач по расчету
оболочек. Остановимся на некоторых приложениях.

5.

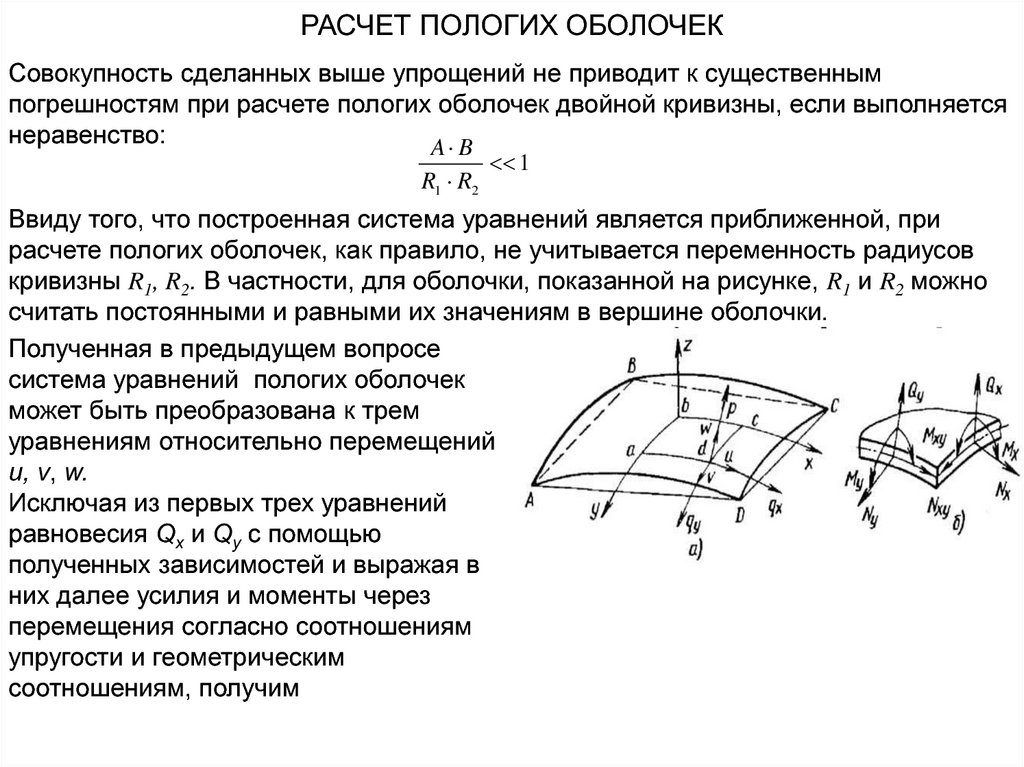
РАСЧЕТ ПОЛОГИХ ОБОЛОЧЕК
Совокупность сделанных выше упрощений не приводит к существенным
погрешностям при расчете пологих оболочек двойной кривизны, если выполняется
неравенство:
A B
R1 R2
1
Ввиду того, что построенная система уравнений является приближенной, при
расчете пологих оболочек, как правило, не учитывается переменность радиусов
кривизны R1, R2. В частности, для оболочки, показанной на рисунке, R1 и R2 можно
считать постоянными и равными их значениям в вершине оболочки.
Полученная в предыдущем вопросе
система уравнений пологих оболочек
может быть преобразована к трем
уравнениям относительно перемещений
и, v, w.
Исключая из первых трех уравнений
равновесия Qx и Qy с помощью
полученных зависимостей и выражая в
них далее усилия и моменты через
перемещения согласно соотношениям
упругости и геометрическим
соотношениям, получим

6.

1
2u 1 2u 1 2 v
w
1 2
2
qx ,
2
2 y
2 x y R1 R2 x
E h
x
1
2 v 1 2 v 1 2u
w
1 2
qy ,
2 x 2
2 x y R2 R1 y
E h
y 2
1
u 1
v 1
1
2
2 2
R1 R2 x R2 R1 y R1 R2 R1 R2
h2
1 2
2 2
w
w
p.
12
E
h
2
2
где 2
2
2
x
y
Если на оболочку не действуют касательные поверхностные нагрузки, т. е. qx=qy=0,
система уравнений пологих оболочек может быть приведена к двум уравнениям.
Введем функцию напряжений φ так, как это было сделано в теории пластин
2
2
2
N x 2 , N y 2 , N xy
x y
y
x
Тогда первые два уравнения равновесия (при qx=qy=0) удовлетворяются
тождественно, а третье уравнение равновесия после исключения Qx, Qy и замены
Мх, Μy, Мху через w, a Nx, Ny — через φ примет вид
1 2 1 2
2 2
D w
p
R1 y 2 R2 x 2

7.

0
0
0
Используя выражения для деформаций x , y , xy и путем их дифференцирования
исключая функции и и v, получим уpавнение совместности деформаций,
аналогичное в теории пластин
2 0
2 0
2 x0 y xy
1 2w 1 2w
y
2
x
2
x y
R1 y
2
R2 x 2
0
0
0
Заменяя x , y , xy через Nx, Ny, Nxy с помощью соотношений упругости и вводя
функцию напряжений φ, получим
1
1 2w 1 2w
2 2
2
2
E h
R1 y
R2 x
Таким образом, теория пологих оболочек сводится к двум уравнениям
относительно прогиба w и функции напряжений φ. Эти уравнения можно привести к
одному уравнению относительно w. Действуя бигармоническим оператором на
уравнение первое уравнение и исключая 2 2 с помощью второго уравнения,
можно записать одно уравнение восьмого порядка
1 2
1 2 1 2w 1 2w
D w E h 2
2 2
2 2 2 p
R2 x R1 y
R2 x
R1 y
2
2
2
2

8.

Для шарнирно опертой по краям прямоугольной в плане пологой оболочки (см. рис)
решение может быть построено путем
разложения искомых функций в двойные
тригонометрические ряды как в теме про
расчет шарнирно опертых прямоугольных
пластин.
Граничные условия в рассматриваемом
случае записываются в следующем виде:
2
2
2 w 2
при x=0 и x=a: w=v=0, 2 2 0 при y=0 и y=b: w=u=0, w 0
2
2
x
y
y
x
Для того чтобы удовлетворить эти граничные условия, искомые функции w и φ
достаточно представить рядами вида
m x
n y
m x
n y
w wmn sin
sin
, mn sin
sin
m 1 n 1
a
b
a
m 1 n 1
b
где wmn, φmn — постоянные коэффициенты разложений, которые необходимо
определить.
Представляя внешнюю нагрузку р(х, у) таким же рядом
m x
n y
p p mn sin
m 1 n 1
a
sin
b
где ртп — известные коэффициенты, и подставляя ряды для w и φ в два уравнения
четвертого порядка, получим алгебраическую систему уравнений для определения
wmn и φmn:

9.

2
m 2 n 2
1
D
w
mn
a
b
R1
1
n
R2
b
2
2
m
mn p mn ,
a
2
2
2
1 n 2 1 m 2
1 m n
mn
wmn 0.
E h a b
R
b
R
a
1
2
Определяя из системы wmn для оболочки, показанной на рисунке, окончательно
получим
2
w x, y
m 1 n 1
m 2 n 2
m x
n y
p mn
sin
sin
a
b
a b
4
m 2 n 2
1 n 2 1 m 2
D
E h
a
b
R
b
R
a
1
2
2

10.

Решение может быть получено и в результате подстановки разложений для w и р
в уравнение восьмого порядка. Полученный ряд для прогиба оболочки w сходится
значительно медленнее соответствующего разложения для пластины, так как
первое слагаемое знаменателя, обеспечивающее его сходимость, содержит малый
коэффициент D, пропорциональный h3.
В случае, когда граничные условия не соответствуют условиям шарнирного
опирания, решение может быть получено методами, рассмотренными в теории
пластин. Значение полученных уравнений не исчерпывается только возможностью
расчета пологих оболочек. Теория пологих оболочек в силу простоты ее уравнений
и достаточной точности в большинстве практических случаев находит также
широкое применение при решении задач локальной деформации оболочек при
действии сосредоточенных нагрузок и задач устойчивости оболочек, когда на ее
поверхности образуются местные складки. Основанием для этого является то, что
на относительно малом участке поверхности оболочка практически всегда может
считаться пологой и соответствующее локальное напряженное состояние может
быть описано полученными выше уравнениями.

11.

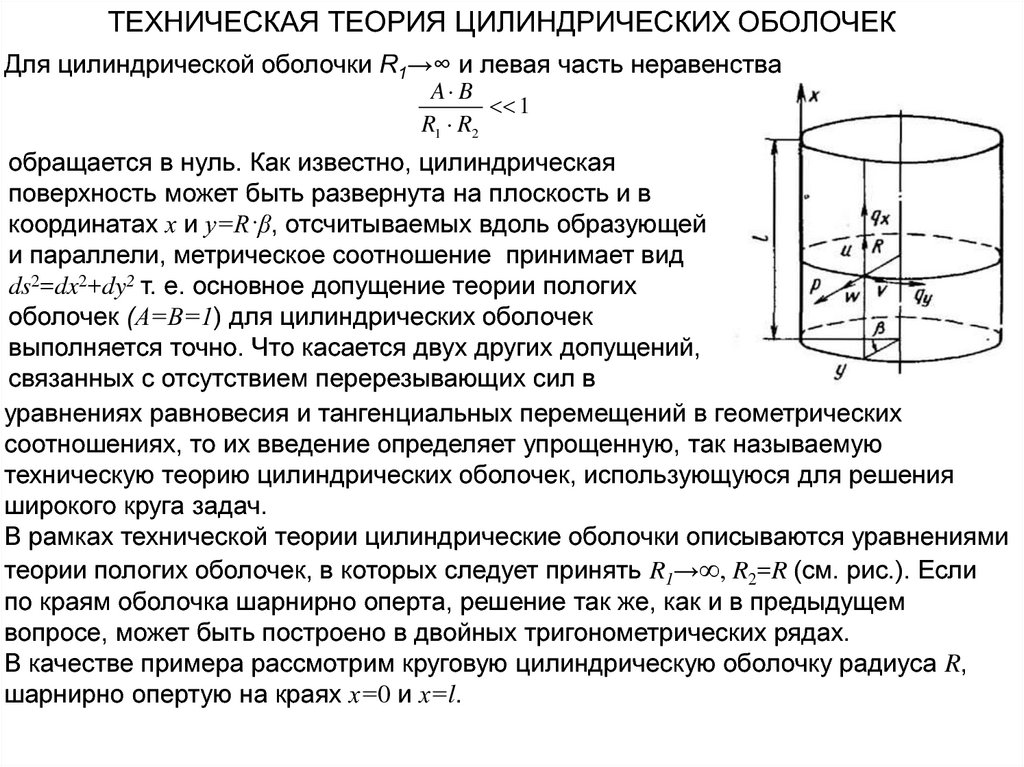
ТЕХНИЧЕСКАЯ ТЕОРИЯ ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК
Для цилиндрической оболочки R1→∞ и левая часть неравенства
A B
1
R1 R2
обращается в нуль. Как известно, цилиндрическая
поверхность может быть развернута на плоскость и в
координатах х и у=R·β, отсчитываемых вдоль образующей
и параллели, метрическое соотношение принимает вид
ds2=dx2+dy2 т. е. основное допущение теории пологих
оболочек (А=В=1) для цилиндрических оболочек
выполняется точно. Что касается двух других допущений,
связанных с отсутствием перерезывающих сил в
уравнениях равновесия и тангенциальных перемещений в геометрических
соотношениях, то их введение определяет упрощенную, так называемую
техническую теорию цилиндрических оболочек, использующуюся для решения
широкого круга задач.
В рамках технической теории цилиндрические оболочки описываются уравнениями
теории пологих оболочек, в которых следует принять R1→∞, R2=R (см. рис.). Если
по краям оболочка шарнирно оперта, решение так же, как и в предыдущем
вопросе, может быть построено в двойных тригонометрических рядах.
В качестве примера рассмотрим круговую цилиндрическую оболочку радиуса R,
шарнирно опертую на краях х=0 и х=l.

12.

Граничные условия на этих краях имеют вид:
2
2w
N x 0 2 0 , v 0, w 0, M x 0 2 0 .
y
x
Пусть на оболочку действует нормальное давление р(х,β),
распределенное симметрично относительно радиальной
плоскости β=0, а тангенциальные нагрузки отсутствуют
(qx=qy=0)
m x
n y
p x, y p mn sin
m 1 n 1
l
cos
R
Подставляя разложения u, v, w и р в полученные уравнения теории пологих
оболочек
1
2u 1 2u 1 2 v
w
1 2
qx ,
2 y 2
2 x y R1 R2 x
E h
x 2
1
2 v 1 2 v 1 2u
w
1 2
2
qy ,
2
2 x
2 x y R2 R1 y
E h
y
1
u 1
v 1
1
2
2 2
R1 R2 x R2 R1 y R1 R2 R1 R2
h2
1 2
2 2
w
w
p.
12
E
h
и приравнивая по отдельности члены левых и правых частей уравнений,
содержащие одинаковые тригонометрические функции, для каждой тройки
неизвестных коэффициентов итп, vmn, wmn получим по три линейных алгебраических
уравнения:

13.

m
l
1
2
2
2
1 m n
m
n
u mn
v mn
wmn 0,
2
l
R
R
l
R
n 2 1
1 m n
u mn
2
l
R
2
R
m
l
m
2
2
h m n
1 2
wmn
p mn .
12 l R
E h
R
l
u mn
1 n
1
v mn 2 wmn
R R
R
2
1 n
v mn wmn 0,
R R
2
2
Решая эти уравнения, можно найти umn, vmn, wmn в зависимости от коэффициентов
разложения нагрузки ртn.
Аналогичным образом решаются и уравнения
1 2 1 2
D w
p
R1 y 2 R2 x 2
2
2
1
1 2w 1 2w
2 2
E h
R1 y 2 R2 x 2
В результате получается система из которой находятся wmn и φmn

14.

ПОЛУБЕЗМОМЕНТНАЯ ТЕОРИЯ ЦИЛИНДРИЧЕСКИХ
ОБОЛОЧЕК
ОСНОВНЫЕ ГИПОТЕЗЫ И ИСХОДНЫЕ СООТНОШЕНИЯ
Цилиндрическая оболочка является распространенным элементом конструкций
самого разнообразного назначения и методы расчета цилиндрических оболочек
разработаны наиболее полно. Уравнения теории цилиндрических оболочек могут
быть получены из уравнений общей теории оболочек, если принять А=В=1, R1→∞,
R2=R. Путем введения некоторых упрощающих предположений в предыдущем
вопросе были получены уравнения технической теории цилиндрических оболочек.
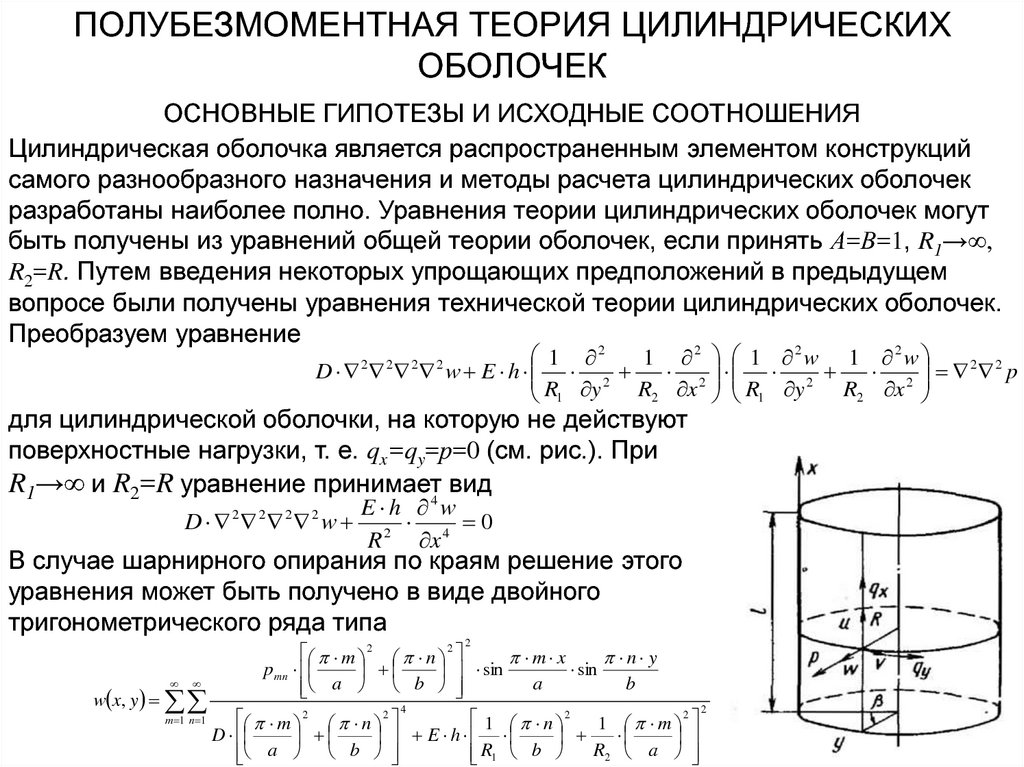
Преобразуем уравнение
2
2
2
2
1
1 1 w 1 w
D 2 2 2 2 w E h 2
2 2
2 2 2 p
R2 x R1 y
R2 x
R1 y
для цилиндрической оболочки, на которую не действуют
поверхностные нагрузки, т. е. qx=qy=р=0 (см. рис.). При
R1→∞ и R2=R уравнение принимает4 вид
D 2 2 2 2 w
E h w
0
R 2 x 4
В случае шарнирного опирания по краям решение этого
уравнения может быть получено в виде двойного
тригонометрического ряда типа
2
w x, y
m 1 n 1
m 2 n 2
m x
n y
p mn
sin
sin
a
b
a b
4
m 2 n 2
1 n 2 1 m 2
D
E h
R2 a
a b
R1 b
2

15.

Для других граничных условий решение данного уравнения в силу его
периодичности по окружной координате у может быть представлено, в виде
w x, y wn x cos
n 0
n y
R
Подставляя данный ряд в решаемое уравнеие и приравнивая нулю коэффициенты
при cos(ny/R), получим для wn(x) обыкновенное дифференциальное Уравнение
восьмого порядка
VIII
n
w
n4
n2
E h IV n 6
n8
VI
wn 6 wn 8 wn 0.
4 2 wn 6 4 2
R
R
R
D
R
R
Решение данного уравнения wn x C ni Fni x содержащее восемь произвольных
i 1
постоянных Cin для каждого n, позволяет удовлетворить любые граничные условия
на краях х=0 и х=l. Однако практическое определение частных решений Fni(x)
уравнения восьмого порядка связано с большими трудностями, что и вызывает
потребность в дальнейшем упрощении теории для снижения порядка уравнения.
Именно такой упрощенной теорией и является рассматриваемая в данном вопросе
полубезмоментная теория цилиндрических оболочек, широко используемая при
решении конкретных задач, в частности, для расчета цилиндрических оболочек
средней длины, нагруженных таким образом, что их деформированное состояние
меняется медленно в продольном направлении. В этой теории наряду с
гипотезами Кирхгофа используются дополнительные упрощающие статические и
кинематические допущения.

16.

Если через sα=х и sβ=s
обозначить координаты точки
срединной поверхности
оболочки, отсчитываемые в
продольном и поперечном
направлениях (рис., а), то
допущения полубезмоментной
теории можно записать в виде
v w
u v
0
0
0,
0, M 0, Q 0, M 0
s R2
s x
То есть в продольном направлении оболочка ведет себя как безмоментная, а в
кольцевом — как система нерастяжимых рам. Полубезмоментная теория особенно
эффективна для расчета оболочек, подкрепленных системой часто
расположенных шпангоутов, которые «размазываются» по длине оболочки,
создавая высокую изгибную жесткость в кольцевом направлении.
Три компоненты перемещения и,v и w связаны между собой двумя
кинематическими условиями, и поэтому при любой форме направляющей они
могут быть представлены, через одну разрешающую функцию Ф(x,s):
Ф
Ф
2Ф
u
, v
, w R2 2
x
s
s
Справедливость данного представления может быть проверена непосредственной
подстановкой в допущения, представленные выше.

17.

Усилие Nα и изгибающий момент Мβ определяются по закону Гука:
u
2Ф
N E h E h
E h 2 ,
x
x
1 2Ф
v w
4Ф
D
M D D
R2 4
2
s R2 s
s
R2 s
0
Здесь в силу сделанного выше замечания о возможности применения
полубезмоментной теории для расчета оболочек, подкрепленных шпангоутами,
введены различные обозначения для жесткостей Eα·h и Dβ. При этом в
полубезмоментной теории влиянием коэффициента Пуассона пренебрегают,
полагая μ=0. Сдвигающее усилие (поток касательных напряжений) в срединной
поверхности оболочки определяется из уравнения равновесия в продольном
направлении:
N
N
3Ф
q E h 3 q
s
x
x
Уравнение для неизвестной функции Ф можно
получить с помощью вариационного принципа
Лагранжа.

18.

Потенциальная энергия деформации полубезмоментной оболочки с учетом
введенных допущений будет иметь вид
2
2Ф
1
1
0
U N M dx ds E h 2 D
2
2
x
2
1 2Ф
4Ф
R2 4 dx ds
2
R
s
s
2
Вариация работы поверхностных нагрузок определяется равенством
Ф
Ф
2 Ф
A q u q v p w dx ds q
q
p R2
dx ds
2
x
s
s
Подставляя полученные выражения в уравнение δU-δA=0 и преобразуя его
интегрированием по частям таким образом, чтобы под поверхностным интегралом
в качестве общего множителя была вариация δФ, получим дифференциальное
уравнение для функции Ф и естественные граничные условия.

19.

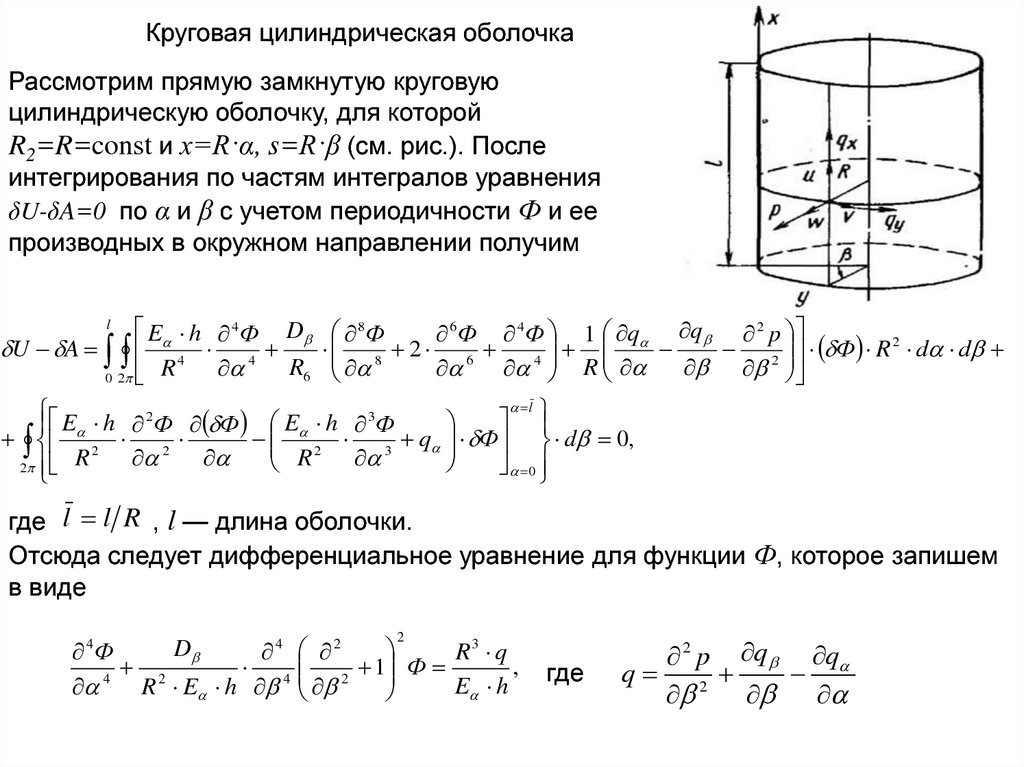
Круговая цилиндрическая оболочка
Рассмотрим прямую замкнутую круговую
цилиндрическую оболочку, для которой
R2=R=const и х=R·α, s=R·β (см. рис.). После
интегрирования по частям интегралов уравнения
δU-δA=0 по α и β с учетом периодичности Ф и ее
производных в окружном направлении получим
E h 4Ф D 8Ф
6Ф 4Ф 1 q q 2 p
2
U A 4 4
8 2
Ф
R
d d
6
4
2
R6
R
0 2 R
l
l
E h 2
3
E
h
Ф
Ф
Ф
2
q
Ф
d 0,
2
R 2 3
R
2
0
где l l R , l — длина оболочки.
Отсюда следует дифференциальное уравнение для функции Ф, которое запишем
в виде
D
4Ф
4
4 R 2 E h 4
2
2
R3 q
2 1 Ф
,
E
h
где
2 p q q
q
2

20.

На торцах полубезмоментной оболочки граничные условия формулируются так же,
как и для безмоментной оболочки — на каждом торце должны быть заданы или
тангенциальные перемещения, или соответствующие им тангенциальные усилия,
т. е. и или Nα, v или Nαβ. Аналогичный результат следует и из вариационного
уравнения. Контурный интеграл представляет вариацию работы реакций на
торцах; он может быть записан в виде
N
l
N
u
Ф
R
d
N
u
N
v
R d
0
R
Чтобы этот интеграл обращался в нуль, на каждом торце должны быть заданы
перемещения (тогда δи=0, δν=0) или должны быть равны нулю соответствующие
им усилия Να=0, Nαβ=0. Поверхностные нагрузки, действующие на круговую
цилиндрическую оболочку, могут быть представлены в форме
тригонометрического ряда по окружной координате β. Например, при нагрузках,
симметричных относительно образующей β=0, правая часть дифференциального
уравнения для Ф может быть записана в виде ряда
R3
q , f n cos n
E h
n 0
Разрешающая функция Φ(α,β) в этом случае находится в виде ряда
Ф Фn cos n
n
где Фn(α) — неизвестные функции.

21.

В силу ортогональности тригонометрических функций решение распадается на
отдельные составляющие. При этом в случае n=0, представляющем
осесимметричное напряженно-деформированное состояние, полубезмоментная
теория неприменима (так как εβ=0) и это состояние рассчитывается отдельно по
безмоментной теории с учетом краевых эффектов. Для первой гармоники (n=1),
представляющей изгиб оболочки как балки, полубезмоментная теория не
учитывает сдвиг (γαβ=0), и поэтому более точное решение можно получить на
основе общей безмоментной теории (здесь также можно учесть краевые эффекты
изгиба).
Для каждой последующей гармоники (n=2,3,...) получим обыкновенное
дифференциальное уравнение
d 4Фn
4 k n4 Фn f n
4
d
где
4 k n4
D
R 2 E h
n4 n2 1
2
Полученное уравнение в отличие от уравнения пологой оболочки имеет уже
четвертый порядок и по виду совпадает с уравнением осесимметричного краевого
эффекта. Его решение можно записать в аналогичной форме
Фn e kn C1 cos k n C 2 sin k n e kn C3 cos k n C 4 sin k n Фn0
0
где Фn — частное решение неоднородного уравнения.

22.

Параметр kn в случае гладкой оболочки (Eα=E, Dβ= Eh3/12) пропорционален
величине h R и при небольших значениях n является достаточно малым.
Вследствие этого деформированное состояние тонкой оболочки при малых n
меняется вдоль образующей медленно. В этом случае удобнее решение записать
через функции А. Н. Крылова:
Фn A1 K1 k n A2 K 2 k n A3 K 3 k n A4 K 4 k n Фn0
Функции А. Н. Крылова имеют вид :
K1 x ch x cos x, K 2 x
1
1
1
ch x sin x sh x cos x , K 3 x sh x sin x, K 4 x ch x sin x sh x cos x ,
2
2
4
Они делятся на симметричные (К1 и К3) и антисимметричные (К2 и К4)
относительно х=0 и их производные выражаются через эти же функции в виде:
K1 x 4 K 4 x , K 2 x K1 x , K 3 x K 2 x , K 4 x K 3 x
Произвольные постоянные Ci или Ai определяются из четырех граничных условий
на торцах оболочки. В случае необходимости решение, полученное по
полубезмоментной теории, при не слишком больших n может быть дополнено
решением в виде осесимметричного краевого эффекта.
Полубезмоментная теория применима для расчета деформаций, медленно
изменяющихся вдоль образующей; для гладкой оболочки это ограничение
определяется неравенством 1 n R h .