2.03M

Category:

mechanics

Основы теории оболочек. Общие сведения о тонких пластинах, продолжение

1.

Строительная механика
ракет-носителей
Контрольный опрос
по лекции 2.1
Общие сведения о тонких пластинах

2.

1. Какие напряжения и деформации в пластине,
согласно гипотезам Кирхгофа, = 0?
х
у
z
xy
yz
zx
х
у
z
xy
yz
zx

3.

2. Упростить геометрические соотношения для пластины,
с учетом гипотез Кирхгофа
E
x 1 2 x ( y z ) ;
E
y ( x z ) ;
y
2
1
E
z ( x y )
z
2
1
xy G xy ;
yz G yz ;
zx G zx

4.

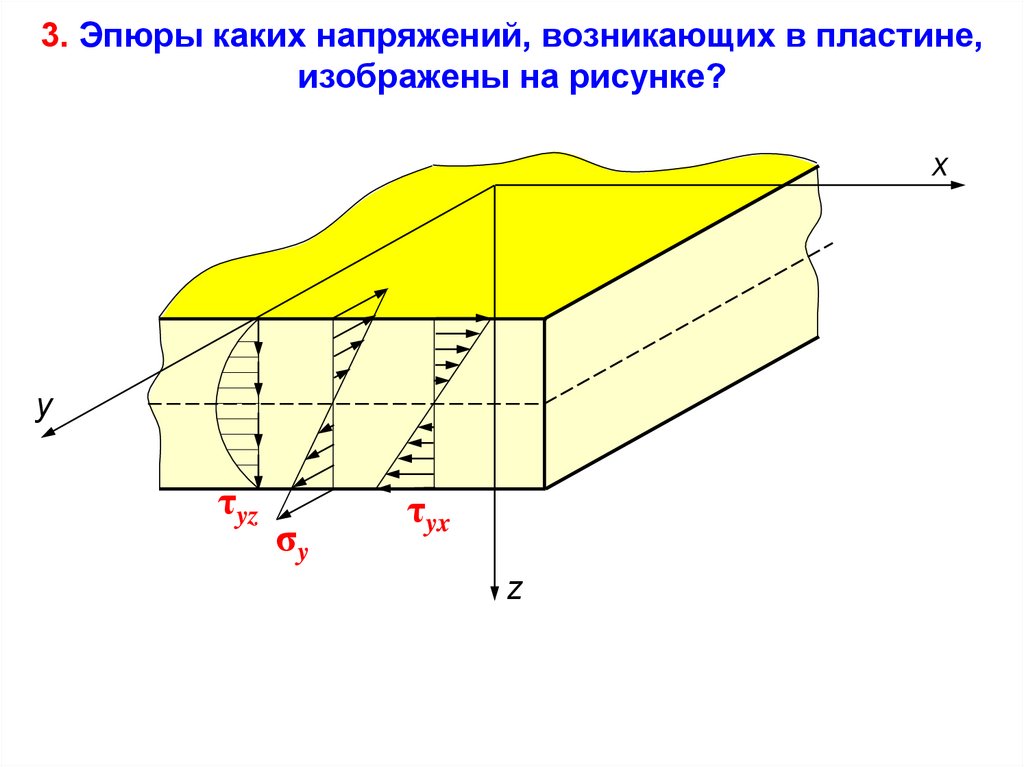
3. Эпюры каких напряжений, возникающих в пластине,
изображены на рисунке?
x
y
z

5.

4. Эпюры каких напряжений, возникающих в пластине,
изображены на рисунке?
x
y
z

6.

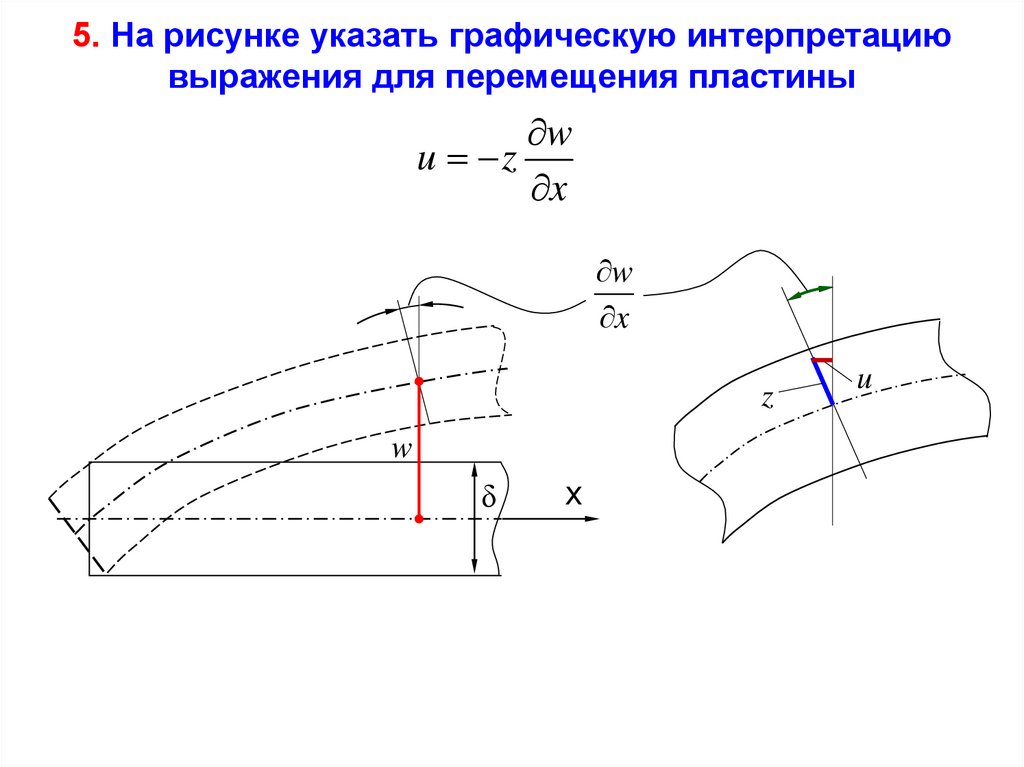
5. На рисунке указать графическую интерпретацию
выражения для перемещения пластины
w
u z
x
δ
x

7.

Строительная механика
ракет-носителей
Ответы на вопросы
по лекции 2.1

8.

1. Какие напряжения и деформации в пластине,
согласно гипотезам Кирхгофа, = 0?
х
у
z
xy
yz
zx
х
у
z
xy
yz
zx

2. Упростить геометрические соотношения для пластины,
с учетом гипотез Кирхгофа
E
xy G xy ;
x 1 2 x ( y z ) ;
E
y ( x z ) ;
yz G yz ;
y
2
1
E
z ( x y )
zx G zx
z
2
1
E
x 1 2 x y ;
E
y x ;
y
2
1
E
xy
xy
2 1

10.

3. Эпюры каких напряжений, возникающих в пластине,
изображены на рисунке?
x
y
τyz
σy
τyx
z

11.

4. Эпюры каких напряжений, возникающих в пластине,
изображены на рисунке?
x
σx
y
τxy
z
τxz

12.

5. На рисунке указать графическую интерпретацию
выражения для перемещения пластины
w
u z
x
w
x
z
w
δ
x
u

13.

Критерии оценки:
Оценка
«отлично» –
«хорошо» –
«удовлетворительно» –
«неудовлетворительно» –
Количество ошибок
0
1
2
3 и более

14.

Строительная механика
ракет-носителей
Тема 2
Основы теории оболочек
Лекция № 10 /2.2/
Старший преподаватель 13 кафедры
Карчин Александр Юрьевич

15.

Строительная механика ракет-носителей
Тема 2 Основы теории оболочек
Лекция 2.2
Общие сведения
о тонких пластинах /продолжение/
Вопрос 4 Статические соотношения для пластин
Вопрос 5 Изгиб круглых пластин /граничные условия/

16.

Строительная механика ракет-носителей
Тема 2 Основы теории оболочек
Лекция 2.2
Общие сведения
о тонких пластинах /продолжение/
Карчин А.Ю., Болдырев К.Б.
Теоретические основы строительной
механики ракет-носителей
СПб.: ВКА имени А.Ф. Можайского, 2015
с. 69-75

17.

18.

Вопрос 4. Статические соотношения для пластин
Рассматривается элемент пластины
z
dy
δ/2
δ
y
x
δ/2
dx
Срединная плоскость

19.

Вопрос 4. Статические соотношения для пластин
На расстоянии z от серединной плоскости необходимо выделить
элементарный участок пластины dz
z
dz
x
z
y
Срединная плоскость

20.

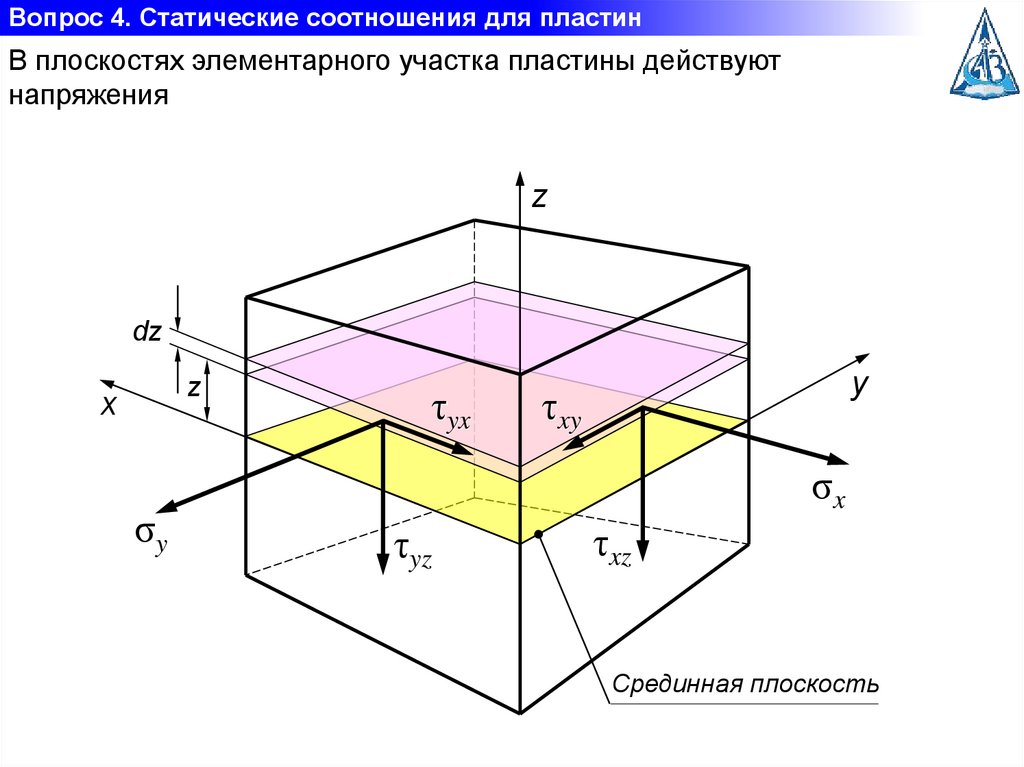
Вопрос 4. Статические соотношения для пластин
В плоскостях элементарного участка пластины действуют
напряжения
z
dz
z
x
σy
τyx
y
τxy
σx
τyz
τxz
Срединная плоскость

21.

Вопрос 4. Статические соотношения для пластин
Эти напряжения являются результатом действия сил и моментов
z
y
x
dz
Syx
Ny
My
Мyx
Qy
Ni – погонные осевые силы
Qi – погонные перерезывающие силы
Sij – погонные сдвигающие силы
Mi – погонные изгибающие моменты
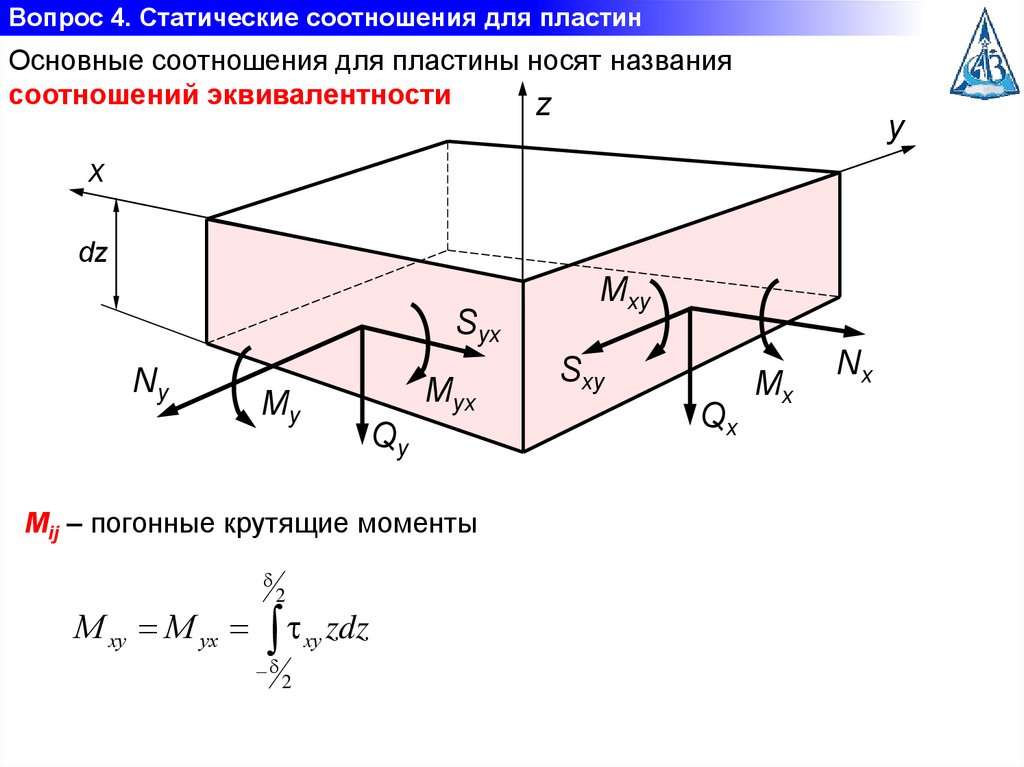
Мij – погонные крутящие моменты
Мxy
Sxy
Qx
Mx
Nx

22.

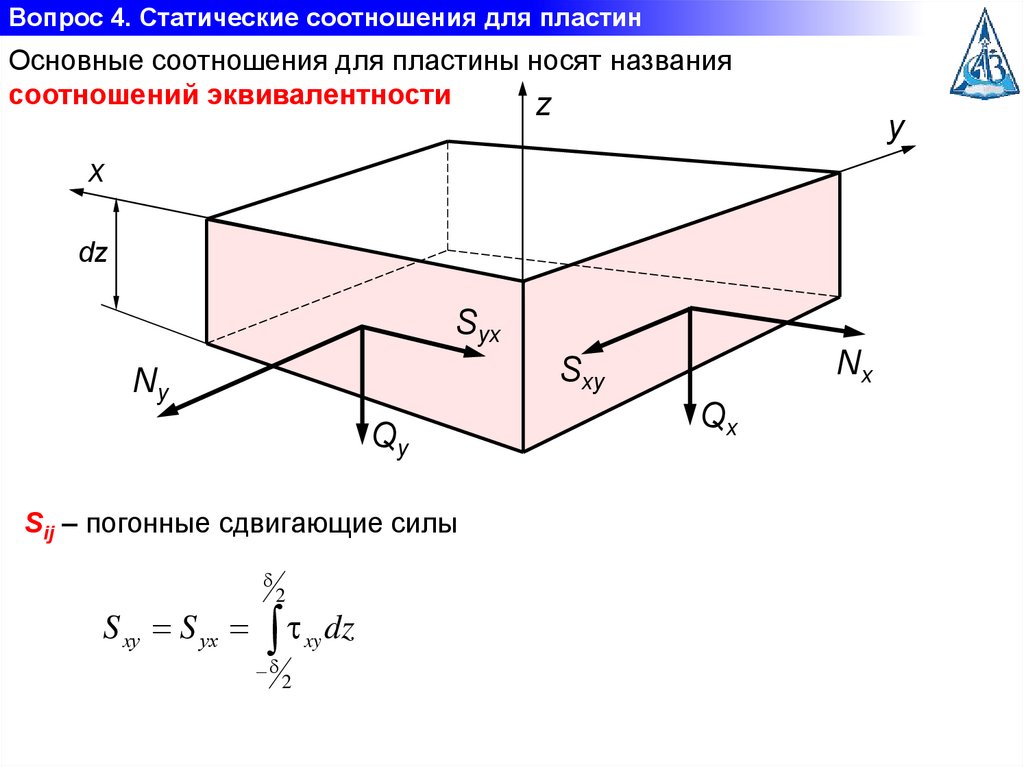
Вопрос 4. Статические соотношения для пластин
Основные соотношения для пластины носят названия
соотношений эквивалентности
z
y
x
dz
Nx
Ny
Ni – погонные осевые силы
Nx
2
dz
x
2
Ny
2
dz
y
2

23.

Вопрос 4. Статические соотношения для пластин
Основные соотношения для пластины носят названия
соотношений эквивалентности
z
y
x
dz
Nx
Ny
Qx
Qy
Qi – погонные перерезывающие силы
Qx
2
2
xz
dz
Qy
2
2
yz
dz

24.

Вопрос 4. Статические соотношения для пластин
Основные соотношения для пластины носят названия
соотношений эквивалентности
z
y
x
dz
Syx
Ny
Qy
Sij – погонные сдвигающие силы
S xу S уx
Nx
Sxy
2
2
xy
dz
Qx

25.

Вопрос 4. Статические соотношения для пластин
Основные соотношения для пластины носят названия
соотношений эквивалентности
z
y
x
dz
Syx
Ny
My
Sxy
Qx
Qy
Mi – погонные изгибающие моменты
Mx
2
zdz
x
2
My
2
2
y
zdz
Mx
Nx

26.

Вопрос 4. Статические соотношения для пластин
Основные соотношения для пластины носят названия
соотношений эквивалентности
z
y
x
dz
Syx
Ny
Мyx
My
Qy
Мij – погонные крутящие моменты
М xу М уx
2
2
xу
zdz
Мxy
Sxy
Qx
Mx
Nx

27.

Вопрос 4. Статические соотношения для пластин
Для определения осевой силы Nx используют выражения для
напряжений
Nx
2
dz
x
Nx
2
2
Е
1 2
2
2w
2w
z 2 2 dz
y
x
Согласно гипотезам, величина w
не зависит от координаты z, →
переменные можно вынести
за знак интеграла
Е
Nx
1 2
w
w 2
2 2 zdz
y
x
2
2
2
Е 2w
2w
z 2 2 ;
x
2
1 дx
дy
Е 2w
2w
z 2 2 ;
y
2
1 дy
дx
Е
2w
xy
z
.
1 x y
интеграл нечётной функции
с противоположными пределами
интегрирования = 0 →
Nx 0

28.

Вопрос 4. Статические соотношения для пластин
Изгибающие моменты Mx определяются аналогично
Е 2w
2w
z 2 2 ;
x
M x x zdz
2
1 дx
дy
2
Е 2w
2w
y
z 2 2 ;
2
2
1 дy
дx
Е 2w
2w
Mx
z 2 2 zdz
2
2
1
x
y
Е
w
xy
z
.
2
1 x y
2
2
2
Е w
w 2
Mx
2 z dz
2
2
D – цилиндрическая жёсткость
1 x
y
2
2
(жёсткость пластины на изгиб)
В результате интегрирования
w
w
M x D 2 2
y
x
2
D включает физические
2
D
E
12 1 2
3
и геометрические
параметры
и характеризует
сопротивляемость
пластины к изгибу

29.

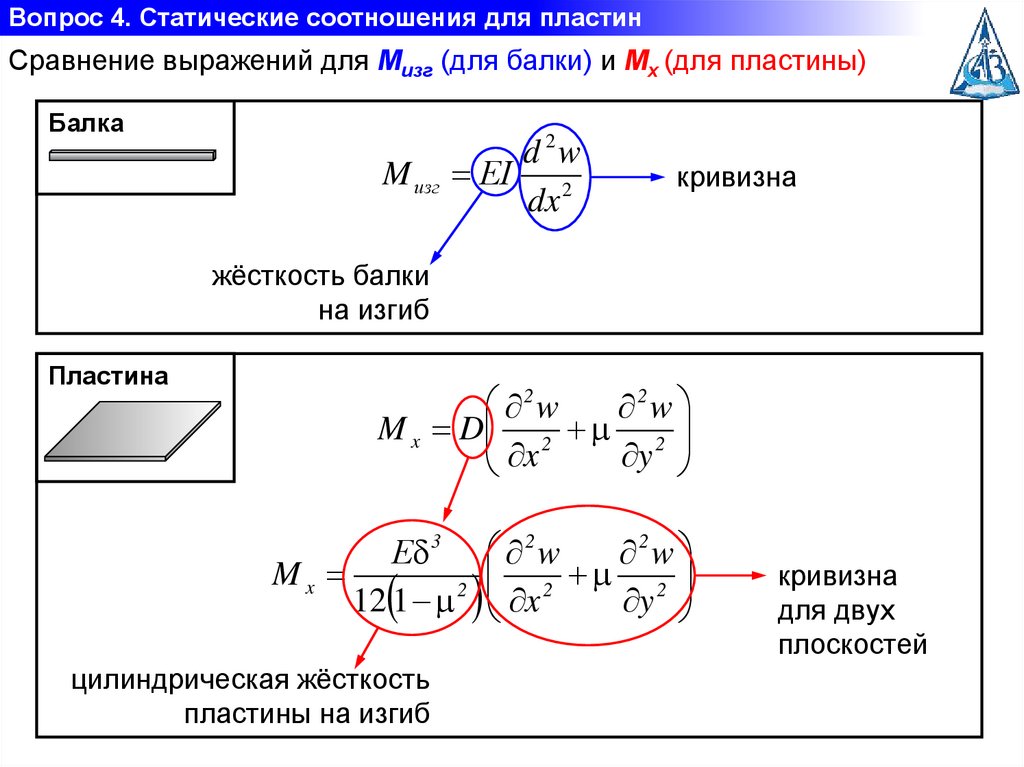
Вопрос 4. Статические соотношения для пластин
Сравнение выражений для Mизг (для балки) и Mх (для пластины)
Балка
M изг
d 2w
ЕI 2
dx
кривизна
жёсткость балки
на изгиб
Пластина
2w
2w
M x D 2 2
y
x
Е 3
Mx
12 1 2
цилиндрическая жёсткость
пластины на изгиб
2w
2w
2 2
y
x
кривизна
для двух
плоскостей

30.

Вопрос 4. Статические соотношения для пластин
Для определения сдвигающей силы Sxy используют выражения для
напряжений
S xy
yx
dz
2
S xy
Е 2w
2w
z 2 2 ;
x
2
1 x
y
Е 2w
2w
z 2 2 ;
y
2
1 y
x
Е
2w
xy
z
.
1 x y
2
2
Е
2w
z
dz
1 x y
2
Е w 2
S xy
zdz
1 x y
2
2
z – нечётная функция →
S xy 0

31.

Вопрос 4. Статические соотношения для пластин
Для определения крутящих моментов Мxy используют выражения для
напряжений
М xy
2
xy
zdz
2
В результате преобразования
и интегрирования
М xy
2w
D 1
x y
Е 2w
2w
z 2 2 ;
x
2
1 x
y
Е 2w
2w
z 2 2 ;
y
2
1 y
x
Е
2w
xy
z
.
1 x y

32.

Вопрос 4. Статические соотношения для пластин
Для определения перерезывающей силы Qx используют выражения
для напряжений
Qx
Qx
2
E
2
2
xz
z
w
2
2(1 ) 4
x
2
dz
2
2
zx
2
2
E
2
2
z
wdz
2
2(1 ) 4
x
2
2
z dz
4
2
E
2 2
Qx
w
2
2(1 ) x
2
w
В результате интегрирования: Qx D
x

33.

Вопрос 4. Статические соотношения для пластин
Внутренние силовые факторы в сечении,
нормаль которого параллельна оси X:
Аналогичным образом определяются внутренние силовые факторы
в сечении, нормаль которого параллельна оси У:
Nx 0
Ny 0
2
Qx D w
x
2
Qy D w
y
Sx 0
Sy 0
2w
2w
M x D 2 2
y
x
2w
М xy D 1
x y
2w
2w
M y D 2 2
x
y
2w
М yx D 1
x y

34.

Вопрос 4. Статические соотношения для пластин
Таким образом, под действием внешней нагрузки в сечениях пластины,
которые перпендикулярны её срединной плоскости, возникают:
2
w
Поперечные силы: Qx D
x
Q y D 2 w
y
2
2
w
w
Изгибающие моменты: M D
x
x 2 y 2
2
2
M D w w
2
у 2
у
x
2
w
Крутящие моменты:
М xy / yx D 1
x y
Все силовые факторы выражены через цилиндрическую жёсткость D
и прогибы w срединной плоскости пластины

35.

Вопрос 4. Статические соотношения для пластин
Из физических уравнений
для пластины:
Е
x
1 2
Из статических соотношений
для пластины:
2w
2w
z 2 2
y
x
2w
2w
M x D 2 2
y
x
или
2w
M
2w
2 2 x
y
D
x
Mx
12(1 2 ) M x
Е
Е
z
x
z
2
2
1
E 3
1
D
x 12 M x
E
12(1 2 )
3
аналогично →
z
3
z
y 12 M y 3

36.

Вопрос 4. Статические соотношения для пластин
z
2
В сечении пластины максимальные по модулю
нормальные напряжения возникают на поверхностях
max
12 M x
x
z
Mx
6M x
2
3
W
Момент инерции площади
прямоугольного сечения (b = 1)
y
х
δ
b 3 3
I
12 12
Момент сопротивления
прямоугольного сечения
с шириной = 1
2 3 2
I
W
12 6
2
аналогично →
b=1
max
x
max
y
6M x
2
6M y
2

37.

Вопрос 4. Статические соотношения для пластин
Из физических уравнений
для пластины:
Из статических соотношений
для пластины:
Е
2w
xy
z
1 x y
М xy / yx
М xy / yx
Е
xy
z
1 D 1
E 3
12(1 2 )
12 М xy / yx
max
xy
3
z
2w
D 1
x y
М ху / ух
2w
или
x y
D 1
6 М xy / yx
2
Сравнение максимальных значений напряжений, при z
2
max
x
6M x
2 ;
max
y
6M y
2
;

38.

Вопрос 4. Статические соотношения для пластин
Для определения вертикальных касательных напряжений,
необходимо сравнить:
Из физических уравнений
для пластины:
E
zx
xz
2
2
1
E
yz
2
zy
2
1
Из статических соотношений
для пластины:
2
2
z 2 w
4
x
2
z 2 2 w
4
y
6Qx
zх
4 z2
6Q y
zy
4 z 2
max
zх
max
zy
2
Qx D x w
Q y D 2 w
y
3Qx
2
3Q y
2
Qx
2
x w D
Q
2w y
y
D
Формулы Журавского
Журавский Дмитрий Иванович (1821-1891) –
русский учёный-механик и инженер, специалист
в области мостостроения и строительной механики

39.

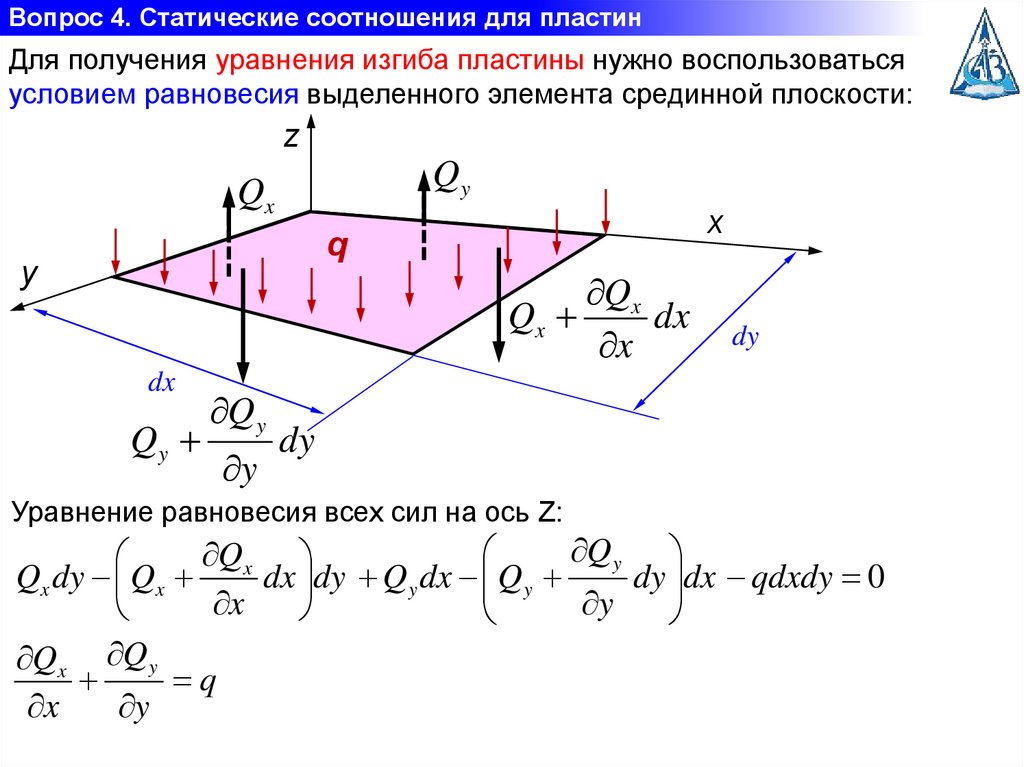
Вопрос 4. Статические соотношения для пластин
Для получения уравнения изгиба пластины нужно воспользоваться
условием равновесия выделенного элемента срединной плоскости:
z
Qy
Qx
x
q
y
Qx
Qx
dx
x
dx
Qy
Q y
y
dy
dy
Уравнение равновесия всех сил на ось Z:
Q y
Qx
dy dx qdxdy 0
Qx dy Qx
dx dy Q y dx Q y
y
x
Qx Q y
q
x
y

40.

Вопрос 4. Статические соотношения для пластин
Уравнение равновесия всех сил на ось Z:
Уравнение моментов относительно оси У:
M x M xy
Qx
x
y
Уравнение моментов относительно оси Х:
M y
y
M yx
x
Qy
уравнение
4
4
4w
w
w
D 4 2 2 4 D 4 w q Софи Жармен
y
x Q x y
Qx
y
q
Софи Жермен (1776-1831) –
x
y
французский математик, философ и механик

41.

Вопрос 4. Статические соотношения для пластин
Сравнение соотношений для балки и пластины
МОМЕНТЫ
Балка
M изг
Пластина
d 2w
EI 2
dx
2w
2w
M x D 2 2
y
x
2
2
w
w
M D
у
2
2
x
у
2w
М xy D 1
x y
2
М D 1 w
yx
x y

42.

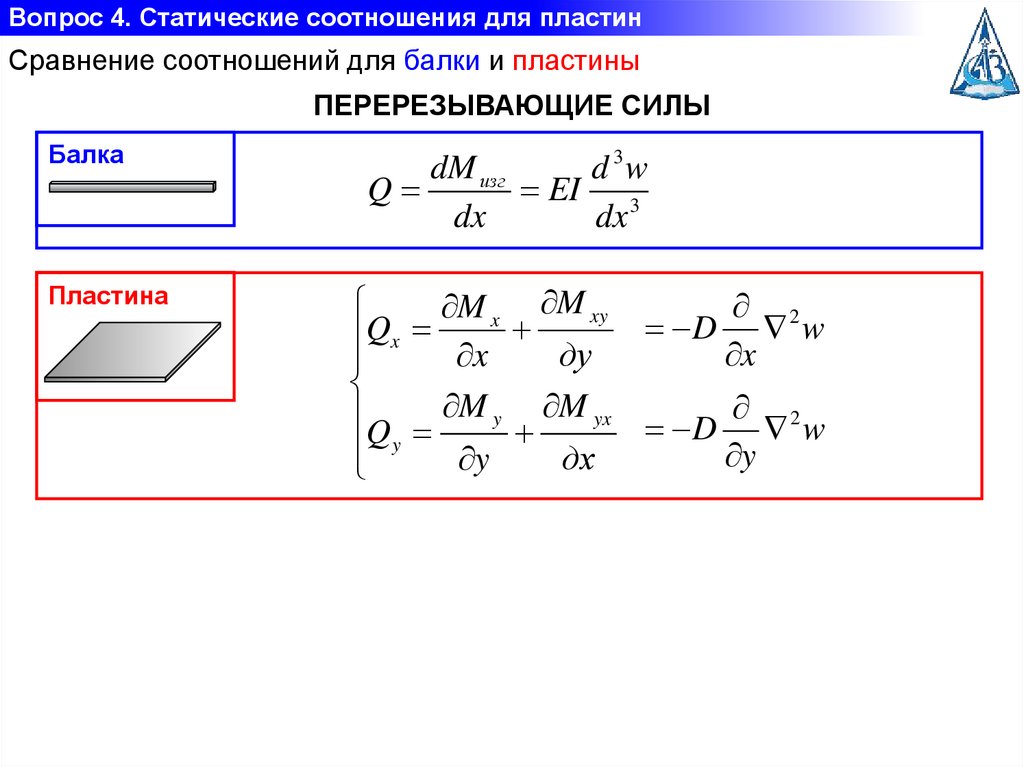
Вопрос 4. Статические соотношения для пластин
Сравнение соотношений для балки и пластины
ПЕРЕРЕЗЫВАЮЩИЕ СИЛЫ
Балка
Пластина
dM изг
d 3w
Q
EI 3
dx
dx
2
M x M xy
D w
Qx
x
x
дy
Q M y M yx D 2 w
y
y
y
дx

43.

Вопрос 4. Статические соотношения для пластин
Сравнение соотношений для балки и пластины
РАСПРЕДЕЛЁННАЯ НАГРУЗКА
Балка
dQ
d 4w
q
EI 4
dx
dx
Пластина
Qx Q y
q
y
x
4w
4w
4w
q D 4 2 2 4 D 4 w
x y
y
x

44.

Строительная механика ракет-носителей
Тема 2 Основы теории оболочек
Лекция 2.1
Общие сведения
о тонких пластинах /продолжение/
Вопрос 4 Статические соотношения для пластин
Вопрос 5 Изгиб круглых пластин /граничные условия/

45.

Вопрос 5. Изгиб круглых пластин
В качестве примера сплошной круглой пластины
с жесткой заделкой краев, нагруженной равномерным давлением:
- мембрана трубопровода
- днище смесительной головки камеры ракетного двигателя
Максимальный прогиб пластины
(из геометрических соотношений)
wmax
pr 4
64 D
E 3
12(1 2 )
σθ
σφ
σφ - нормальные меридиональные напряжения
σθ - нормальные окружные напряжения

46.

Вопрос 5. Изгиб круглых пластин
С учетом максимального прогиба (из физических соотношений)
получают выражения для изгибающих моментов
В заделке:
р
pr 2
M
8
pr 2
M
8
r
Mθ
Mφ
В центре пластины:
pr 2
M M
(1 )
16
2
pr
8
pr 2
1
16
pr 2
8
максимальный
изгибающий момент
M max
pr 2
8

47.

Вопрос 5. Изгиб круглых пластин
Из соотнесений эквивалентности для пластины получают значения
нормальных напряжений
- для окружных напряжений:
max
6M
3 pr 2
2
2
4
- для меридиональных напряжений:
max
6M
2
3 pr 2
4 2
*
Максимальные напряжения в этом виде закрепления пластины будут
возникать в жесткой заделке
Выражение * используется для определения минимального значения
толщины δmin пластины
min
3 pr 2
4 max

48.

Вопрос 5. Изгиб круглых пластин
Второй вариант закрепления сплошной круглой пластины –
шарнирно опертая по контуру и нагруженная равномерным
давлением
р
В местах опор:
pr 2
1
M
8
M 0
r
pr 2
3
16
Mθ
2
pr
1
8
В центре пластины:
pr 2
M M
(3 )
16
Mφ
максимальный
изгибающий момент
M
max
( )
pr 2
(3 )
16

49.

Вопрос 5. Изгиб круглых пластин
Второй вариант закрепления сплошной круглой пластины –
шарнирно опертая по контуру и нагруженная равномерным
давлением
р
r
Максимальный прогиб
пластины
(из геометрических
соотношений)
wmax
5 pr 4
1 64 D

50.

Вопрос 5. Изгиб круглых пластин
Сравнивая значения максимальных моментов для первого и второго
вариантов закрепления пластины
M max .2 pr 3 8
3
2
1,65
M max .1
16
pr
2
2
0,3
Величина максимального момента для шарнирно опертой пластины
(вариант 2) более чем в 1,5 раза больше, чем для пластины с жестко
заделанными краями (вариант 1)
В прикладных задачах приходиться сравнивать прогибы различных
пластин
wmax .2 5 pr 4 64 D 5
4
4
wmax .1 1 64 D pr
1
Максимальный прогиб шарнирно опертой пластины (вариант 2),
будет в четыре раза больше прогиба пластины в жесткой заделке
(вариант 1)

51.

52.

Строительная механика ракет-носителей
Тема 2 Основы теории оболочек
Лекция 2.2
Общие сведения
о тонких пластинах /продолжение/
Вопросы для самоконтроля:
Как называют статические соотношения для пластин?
Какие силовые факторы действуют в пластине?
Что характеризует цилиндрическая жёсткость D?
Какие существуют способы крепления пластин?
При каком закреплении пластины на нее действует максимальный
момент?
6. При каком закреплении пластины в ней возникает максимальный
прогиб?
1.
2.
3.
4.
5.

53.

54.

English Русский Rules