Интерполирование с кратными узлами

1. Интерполирование с кратными узлами

2.

Пусть на промежутке
a, b D f
функция задана
таблично, а также известны некоторые её производные. Узлы, в
которых заданы производные (любого порядка), называются
кратными узлами
x0 , f 0 , f 0 , f 0 , , f 0
m0 1
m0 −кратность x0
m1 1
x1 , f1 , f1 , f1 , , f1
m1 −кратность x1
mn 1
xn , f n , f n , f n , , f n
mn −кратность xn
s m0 m1 m2 mn

3.

Найти многочлен Q x степени s 1 , такой, что:
m 1
m 1
Q x0 f x0 , Q x0 f x0 , , Q 0 x0 f 0 x0 ,
Q xn f xn , Q xn f xn , , Q mn 1 xn f mn 1 xn .
Многочлен Эрмита
Утверждение. Многочлен Qs 1 x , удовлетворяющий
условиям эрмитовой интерполяции, существует и он
единственный.

4.

Доказательство.
1) Единственность (от противного).
~
Пусть существует ещё один многочлен Qs 1 x ,
удовлетворяющий условиям задачи. Найдём их разность.
~
Qs 1 x Qs 1 x
− многочлен степени s 1 или ниже
Имеет s коней (с учётом их кратностей), т.к.
~
~
~
Q x0 Q x0 0 Q x0 Q x0 Q m0 1 x0 Q m0 1 x0
~
Q xn Q xn 0
m0 m1 m2 mn s
Но многочлен степени s−1 не может иметь более s−1 корней,
~
Q
x
Q
следовательно
s 1
s 1 x 0 , т.е. многочлены совпадают.

5.

2) Существование.
Будем строить алгоритм нахождения многочлена Q x . Что и
будет доказательством его существования.
Будем искать многочлен, проходящий через s узлов.
Введём узлы xij xi j 1 , где 0,
i 0, n,
j 1, mi ,
и
При достаточно малом
xij xi
0
все
xij различны.
Строим таблицу разделённых разностей

6.

x01
f x01
f x01
, x02
x02
f x02
f x02
, x03
x0m
0
f x0m
0
f x0 m0 , x11
x11
f x11
f x11
, x12
xnm
n
f xnm
n
f x01
, x02
, x03
f x01
, , xnm
n

7.

Выпишем многочлен Ньютона
f x01 , x02 x x01
Qs 1 x f x01
x x01 x x02
f x01
, x02
, x03
f x01
, x02
, , xij , , xnm
x
x
x
x
x
x
01
ij
nmn 1
n
f x pl , , xkt
f x pl 1 , , xkt
xkt x pl
при
p k
Выразим разделённые разности через производные
t l
f
xi
Когда p k
f x pl , , xkt
t l !
p
f
xi
т.е.
f xi , , xi
p!
p 1, 0

8.

Переходя к пределу 0 получим:
f x0
2
x x0
Qs 1 x f x0 f x0 x x0
2!
f x0 , x0
f x0 , x0 , x0
f x0 , , xn x x0
m0
x x1 m1 x xn mn 1
Пример. Сведения о некоторой функции y f x
представлены следующей дискретной информацией:
f xi
f xi
-1
0
-2
1
0
1
0
2
1
0
2
i
0
xi
f xi
-4

9.

Рассчитаем кратности узлов
x0 1 m0 2
x1 0 m1 3
s 2 3 2 7
x2 1 m2 2
Следует строить многочлен степени
s 7 1 6

10.

i xi f xi
f xi
f xi , xi 1
2
0 -1
0
1 -1
0
2
0
1
0
3
0
1
0
4
0
1
0 1
1
1 0
5
1
0
2
6
1
0
1 0
1
0 1
f xi
2
f xi , xi 2
1 2
3
0 1
0 1
1
0 1
4
2
2
1 0
1
1 0
2 1
3
1 0
f xi , xi 3
f xi , xi 4
f xi , xi 5
4
3
1
1
1
1
1
3
4
f x , x
i 6
i
1

11.

Q x 0 2 x 1 3 x 1 4 x 1 x 0 3 x 1 x 2
2
2
2
1 x 1 x 1 x 1 x3 x 1 x6 2 x 2 1
2
3
2
Для s 1 −кратно дифференцируемой функции
f x
остаточный член интерполяционного многочлена имеет вид
f s 1
m0
m1
mn
x x0 x x1 x xn
Rs x
s 1 !
x0 , xn

12.

Если все узлы простые (однократные), то многочлен Эрмита
есть многочлен Лагранжа:
Qs 1 x Ln x
Если вся информация об f x сосредоточена в одном узле xi ,
то есть xi узел кратности n+1, то многочлен Эрмита это просто
многочлен Тейлора с остаточным членом
f n 1
x xi n 1
n 1 !

13.

Сплайн – интерполяция
Кубический сплайн

14.

Сплайн – некоторая математическая модель гибкого тонкого
стержня из упругого материала.
Определение. Сплайном S m x
называется определённая на
a, b функция l раз непрерывно дифференцируемая
Sm x C l a, b , такая, что на каждом промежутке xi 1, xi
отрезке
i 1, n – это многочлен m-й степени. Разность между
степенью сплайна m и показателем его гладкости l называется
дефектом сплайна d m l

15.

Прикладное применение.
Задача проведения гладкой кривой через точки, произвольным
образом лежащие на плоскости, имеет прикладное применение.
Допустим, имеется передвижная лаборатория, установленная на
автомобиле, которая двигается по дороге и записывает свои
географические координаты на жесткий диск бортового
компьютера через определенные интервалы времени.

16.

Лаборатория вычисляет координаты по данным, получаемым со спутников
GPS (Global Positioning System − глобальной системы позиционирования) и
инерциальной навигационной системы. Координаты записываются как во
время движения лаборатории, так и в моменты её временных остановок.
Требуется получить траекторию движения лаборатории, проведя гладкую
интерполяционную кривую через точки, записанные во время проведения
заезда. Траектория должна не иметь изломов в местах остановки лаборатории,
когда точки траектории имеют одинаковые координаты. Эта задача решается с
использованием
кубических
разбиением параметра t.
сплайнов
с
неравномерным
сеточным

17.

Примеры сплайнов:
Кусочно-линейная функция
a1 x b1 , x x0 , x1
a2 x b2 , x x1 , x2
S1 x
a3 x b3 , x x2 , x3
y
x0
x1 x2 x3
x
Степень сплайна – 1, дефект – 1.

18.

Определение. Кубический сплайн дефекта 1,
интерполирующий функцию f x есть функция
S x Sk x ak bk x xk ck x xk d k x xk
2
x xk 1 , xk
n
k 1
удовлетворяющая совокупности условий:
1. S xk f k
2. S xk C 2 a, b
3. S x0 S xn 0
d m l
3

19.

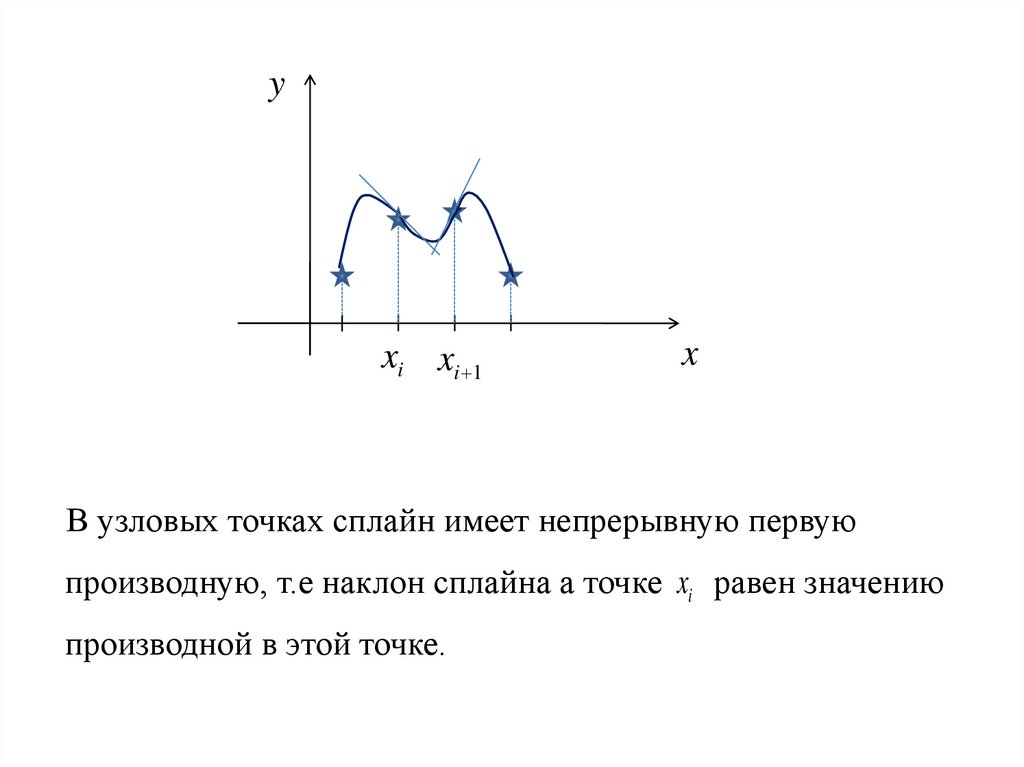
y
xi xi 1
x
В узловых точках сплайн имеет непрерывную первую
производную, т.е наклон сплайна а точке xi равен значению
производной в этой точке.

20.

Дано:
x0 x1 x2 xn
f0
f 0
f1
f1
f2
f 2
fn
f n
Найти сплайн
Рассмотрим отрезок xi , xi 1
Вывод: строим интерполяционный многочлен с кратными
узлами
xi − кратность 2
xi 1 − кратность 2
2 2 1 s − степень многочлена

21.

Составим таблицу разделённых разностей
xi
fi
f i
xi
fi
f i 1 f i
xi 1 xi
xi 1
f i 1
xi 1
f i 1
f i 1 f i
f i
2
xi 1 xi xi 1 xi
f i 1 xi 1 xi f i 1 f i
xi 1 xi 2
f i 1
f i 1 xi 1 xi 2 f i 1 f i f i xi 1 xi
xi 1 xi 3

22.

S3 x f i
fi 1 fi fi xi 1 xi
2
fi x xi
x xi
2
xi 1 xi
fi 1 xi 1 xi 2 fi 1 fi fi xi 1 xi
2
x xi 1 x xi
3
xi 1 xi
Если неизвестны наклоны сплайна (т.е. значения производной
в узлах), вычисляют их примерное значение по формулам
численного дифференцирования.

23.

Пример
Функция задана в виде таблицы
xi
1
2
3
4
fi
0,5
-1
-0,5
5
2,000 0,923 x 0,866 x2 0,289 x3 , x 2
S3 x 0,149 2,300 x 2,477 x2 0,557 x3 , x 3
1,859 0,293 x 1,808 x2 0,483 x3 , x 4