Интерполирование и экстраполирование функции

1.

12.05.2024
БИК Специальность ПОВТ
Дисциплина "Численные методы"
1

2.

Температура, 0С
5
7
13
15
10
3
Время
суток, ч
0
5
10
15
20
24
Чему была равна
температура в 12
часов????
15
10
5
0
12.05.2024
5
10Специальность ПОВТ
15
БИК
Дисциплина "Численные методы"
20
2

3.

Математическая постановка задач интерполирования
Пусть на отрезке [а, b] задана функция у = f(x)
y0 = f(x0), у1 = f(x1), …, уn = f(xn)
х0, х1 ,..., хn - узлы интерполяции
F(х) -табулированная функция
y0 у1 … уn
x0 x1 … xn
yо = F(х0) = f(xо), y1 = F(х1) = f(x1),..., yn = F(хn) = f(xn)
12.05.2024
БИК Специальность ПОВТ
Дисциплина "Численные методы"
3

4.

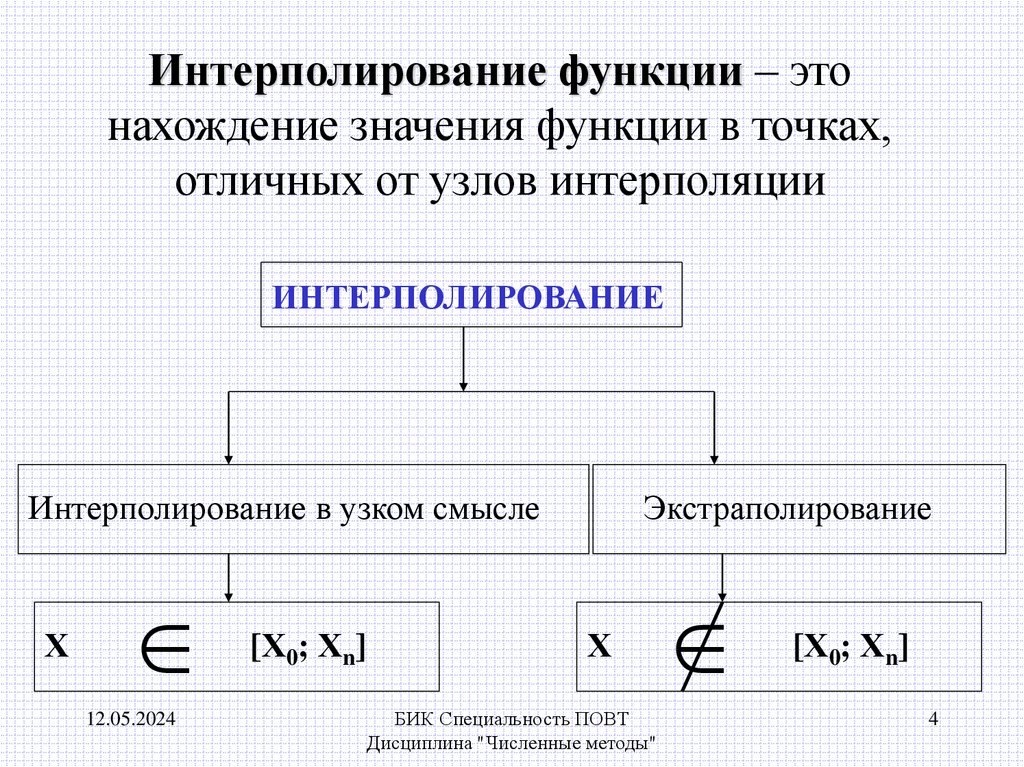
Интерполирование функции – это
нахождение значения функции в точках,
отличных от узлов интерполяции
ИНТЕРПОЛИРОВАНИЕ
Интерполирование в узком смысле
Х
12.05.2024
[Х0; Хn]
Экстраполирование
Х
БИК Специальность ПОВТ
Дисциплина "Численные методы"
[Х0; Хn]
4

5.

Fn(х0) = y0, Fn(х1) = y1, …, Fn(хn) = yn
Fn(х) - интерполяционный многочлен
12.05.2024
БИК Специальность ПОВТ
Дисциплина "Численные методы"
5

6.

При интерполировании функцию, заданную ее
значениями в узлах интерполяции (то есть, с
помощью таблицы) заменяют формулой
(аналитическое задание функции)
Интерполирование с
помощью многочлена
Лагранжа
Интерполирование с
помощью многочлена
Ньютона
Равноотстоящие узлы интерполяции: h=xi-xi+1=const
Неравноотстоящие узлы интерполяции: h=xi-xi+1=const
12.05.2024
БИК Специальность ПОВТ
Дисциплина "Численные методы"
6

7.

Задача:
y0 = f(x0), у1 = f(x1), …, уn = f(xn)
L(x) – многочлен Лагранжа
Ln(х0) = y0
Ln(х1) = y1
…
Ln(хn) = yn
12.05.2024
БИК Специальность ПОВТ
Дисциплина "Численные методы"
7

8.

1) Узлы интерполяции неравноотстоящие
h=xi-xi+1
const
Ln(х) = a0 + а1х + а2х2 + ... + аnхn
12.05.2024
БИК Специальность ПОВТ
Дисциплина "Численные методы"
8

9.

+
+
12.05.2024
БИК Специальность ПОВТ
Дисциплина "Численные методы"
9

10.

Сокращенный вид интерполяционного
многочлена Лагранжа
( x x0 )...( x xi 1 )( x xi 1 )...( x xn )
Ln ( x) yi
( xi x0 )...( xi xi 1 )( xi xi 1 )...( xi xn )
i 0
n
12.05.2024
БИК Специальность ПОВТ
Дисциплина "Численные методы"
10

11.

Пример 1. Функция задана таблично
Пользуясь интерполяционным
многочленом Лагранжа, найти ее значение в точке х = 4.
Решение.
Подставляя в формулу х=4, получим
Вычислмть самостоятельно
12.05.2024
БИК Специальность ПОВТ
Дисциплина "Численные методы"
11

12.

2) Узлы интерполяции равноотстоящие
h=xi-xi+1 =const
Пусть q=(x-x0)/h
q(q 1)...( q n)
n i C
Ln ( x)
( 1)
yi
n!
q i
i 0
n
i
n
n!
C
i!(n i )!
i
n
12.05.2024
БИК Специальность ПОВТ
Дисциплина "Численные методы"
12

13.

Оценка погрешности
интерполяционного многочлена Лагранжа
Rn ( x) f ( x) Ln ( x)
M n 1
Rn ( x)
( x x0 )( x x1 )...( x xn )
(n 1)!
(n+1)
М n+1 = max I f (x) I
12.05.2024
БИК Специальность ПОВТ
Дисциплина "Численные методы"
13

14.

Конечные разности
yi yi 1 yi
n 1
y
( )
n
y
12.05.2024
конечная разность первого порядка
конечная разность n-го порядка
БИК Специальность ПОВТ
Дисциплина "Численные методы"
14