СМО M/G/1/∞, СМО с многомерным входящим потоком, СМО с приоритетами. Характеристики СМО. (Лекция 5)

1. СМО M/G/1/, СМО с многомерным входящим потоком, СМО с приоритетами. Характеристики СМО.

СМО M/G/1/ , СМО с
многомерным входящим
потоком, СМО с приоритетами.
Характеристики СМО.
Лекция 5

2. Одноканальная СМО с произвольной длительностью обслуживания и неограниченной очередью – СМО М/G/1/∞

Время обслуживания заявки распределено по
произвольному (General) закону В(t) с плотностью
вероятности b(t).
Среднее время
обслуживания
0
0
t d B(t ) t b(t )dt
Второй начальный ( 2) t 2 d B(t ) t 2 b(t )dt
0
0
момент
СГУ, ИТ и КС, Курс "МВПиС". Лекция 5
2

3. СМО М/G/1/∞ в стационарном режиме :  = Ƭ < 1

СМО М/G/1/∞ в стационарном
режиме : = Ƭ < 1
В произвольный момент t в очереди находится L
заявок
поступает очередная заявка
дисциплина обслуживания – FIFO
среднее время W__ожидания
заявки
в очереди
__
__
W Т
0
Т 1
Т0 – время, необходимое для завершения
обслуживания ранее выбранной заявки,
Т1 – время на облуживание заявок, стоящих в очереди
перед поступившей заявкой.
СГУ, ИТ и КС, Курс "МВПиС". Лекция 5
3

4. СМО М/G/1/∞

СГУ, ИТ и КС, Курс "МВПиС". Лекция 5
4

5.

__
W w,
__
T 1 L ,
L w
L – средняя длина очереди,
Ƭ - среднее время обслуживания,
- интенсивность входного потока.
__
T 1 w w w,
где - загрузка СМО, < 1.
__
__
w T0 w ,
T0
w
1
СГУ, ИТ и КС, Курс "МВПиС". Лекция 5
(1)
5

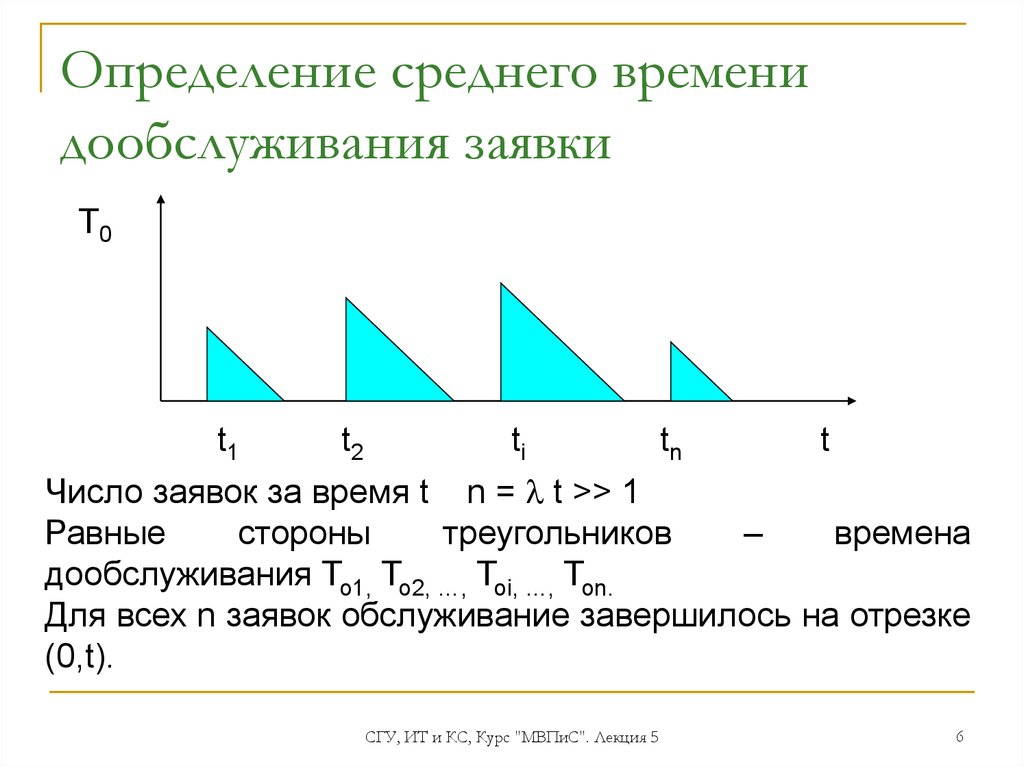
6. Определение среднего времени дообслуживания заявки

Т0
t1
t2
ti
tn
t
Число заявок за время t n = t >> 1
Равные
стороны
треугольников
–
времена
дообслуживания То1, То2, …, Тоi, …, Тоn.
Для всех n заявок обслуживание завершилось на отрезке
(0,t).
СГУ, ИТ и КС, Курс "МВПиС". Лекция 5
6

7. Определение среднего времени дообслуживания заявки

t
1
T 0 T0 (t )dt
t0
1 n (t )
1 n (t ) 1 2
T0 Si Ti ,
t i 1
t i 1 2
1 ( 2)
T0
2
(2)
1 n(t )
1 n (t ) 2
T0
*
Ti ,
2 t
n(t ) i 1
h (t )
1
n(t )
Ti 2
T0 lim
lim (
)
n(t )
2 t t t i 1
СГУ, ИТ и КС, Курс "МВПиС". Лекция 5
7

8. Характеристики СМО М/G/1/

Характеристики СМО М/G/1/
Формула Поллячека
–Хинчина
W
Данные для расчета:
• интенсивность входного потока ,
• среднее время обслуживания Ƭ
• второй начальный момент Ƭ(2)
( 2)
2(1 )
u w
(4),
2(1 )
( 2)
(3)
где u – ср. время пребывания заявки в системе
СГУ, ИТ и КС, Курс "МВПиС". Лекция 5
8

9. Характеристики СМО М/G/1/

Характеристики СМО М/G/1/
L- среднее число заявок в очереди
L w
2 ( 2)
2(1 )
(5)
n – среднее число заявок в системе
n L
2 ( 2)
2(1 )
СГУ, ИТ и КС, Курс "МВПиС". Лекция 5
(6)
9

10. Проверка формулы Поллячека – Хинчина

Формула для расчета среднего времени пребывания в
очереди для СМО М/М/1/ :
2
w
1 1
1
1
Для экспоненциального распределения Ƭ(2) = 2 Ƭ2
подставим в формулу (3) и получим:
2
w
2(1 ) 1
2
СГУ, ИТ и КС, Курс "МВПиС". Лекция 5
2
10

11. СМО с многомерным входным потоком

где
n - число типов
заявок;
i и Ƭi, i = 1…n,
загрузка
заявками i-го типа
i = i Ƭi.
коэффициент
простоя СМО
=1–R
СГУ, ИТ и КС, Курс "МВПиС". Лекция 5
11

12. СМО с многомерным входным потоком

Условие
стационарности:
0
1
Для многоканальных СМО:
n
R
i 1
i
n
i 1
i 1
СГУ, ИТ и КС, Курс "МВПиС". Лекция 5
12

13.

Характеристики заявок i-го типа: wi,
ui, Li, ni.
Вероятность появления заявок i-го типа:
i
Pi
0
Ср. время пребывания заявки i-го типа в очереди:
n
1
( 2)
Wi W
i i
2(1 R ) i 1
СГУ, ИТ и КС, Курс "МВПиС". Лекция 5
13

14. Характеристики СМО при многомерном потоке

Ср. длина очереди заявок i-го типа:
Li Wi i W i
Ср. время пребывания заявки i-го типа в системе:
ui W i
Ср. число заявок i-го типа в системе:
ni i Li
СГУ, ИТ и КС, Курс "МВПиС". Лекция 5
14

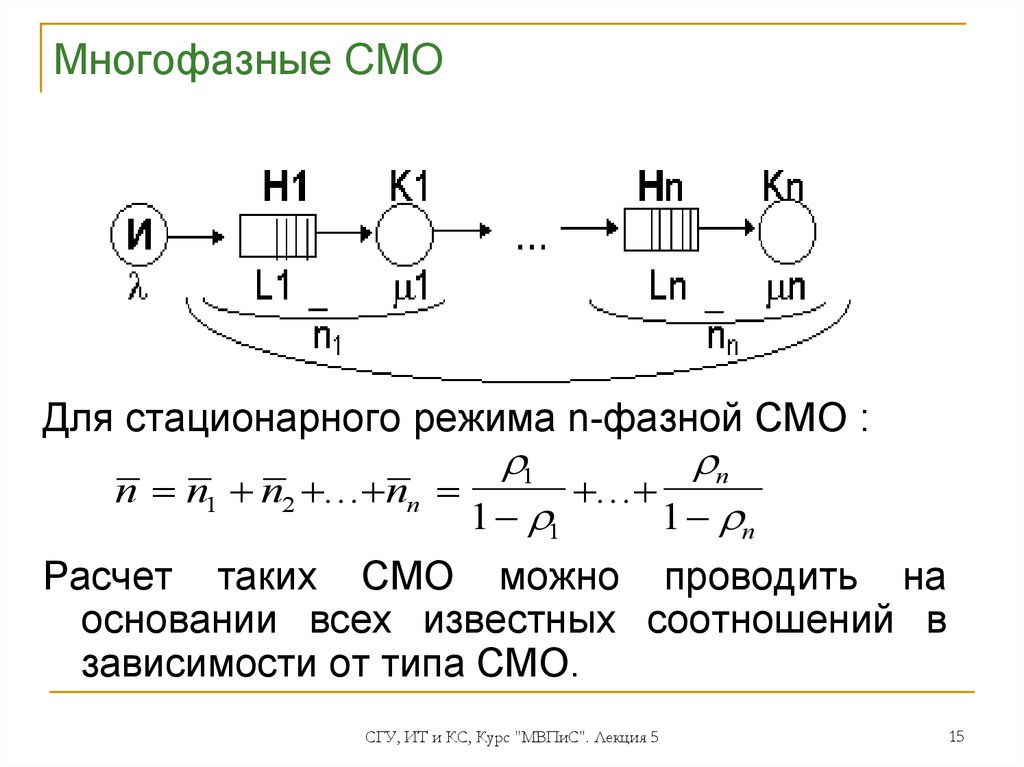
15. Многофазные СМО

Для стационарного режима n-фазной СМО :
1
n
n n1 n2 ... nn
...
1 1
1 n
Расчет таких СМО можно проводить на
основании всех известных соотношений в
зависимости от типа СМО.
СГУ, ИТ и КС, Курс "МВПиС". Лекция 5
15

16. Системы массового обслуживания с приоритетами и их характеристики

17. СМО с приоритетами

Во многих СМО доход (или потери) зависят
от времени пребывания заявки в CМО:
Д = kД / u, (1)
П = kП*u, (2)
u = w + Ƭ (3)
Ƭ − уменьшается, если увеличить скорость
обслуживания = 1/Ƭ.
w − можно уменьшить за счет увеличения
времени ожидания других заявок, назначая
приоритеты.
СГУ, ИТ и КС, Курс "МВПиС". Лекция 5
17

18. СМО с приоритетами

Приоритет – это преимущество в очереди,
характеризуется натуральным числом:
1, 2, …, М.
Приоритеты: относительный и абсолютный,
смешанный.
Относительный приоритет не прерывает
обслуживание уже поступившей в канал
заявки.
СГУ, ИТ и КС, Курс "МВПиС". Лекция 5
18

19. Организация обслуживания с относительными приоритетами

Заявки k-го приоритета накапливаются в
очереди Оk.
Дисциплина обслуживания в очереди Оk –
FIFO.
Заявки из (k+1)-й очереди не выбираются
на обслуживание, если есть хотя бы одна
заявка в k-й очереди, k = 1, 2, …, М – 1.
СГУ, ИТ и КС, Курс "МВПиС". Лекция 5
19

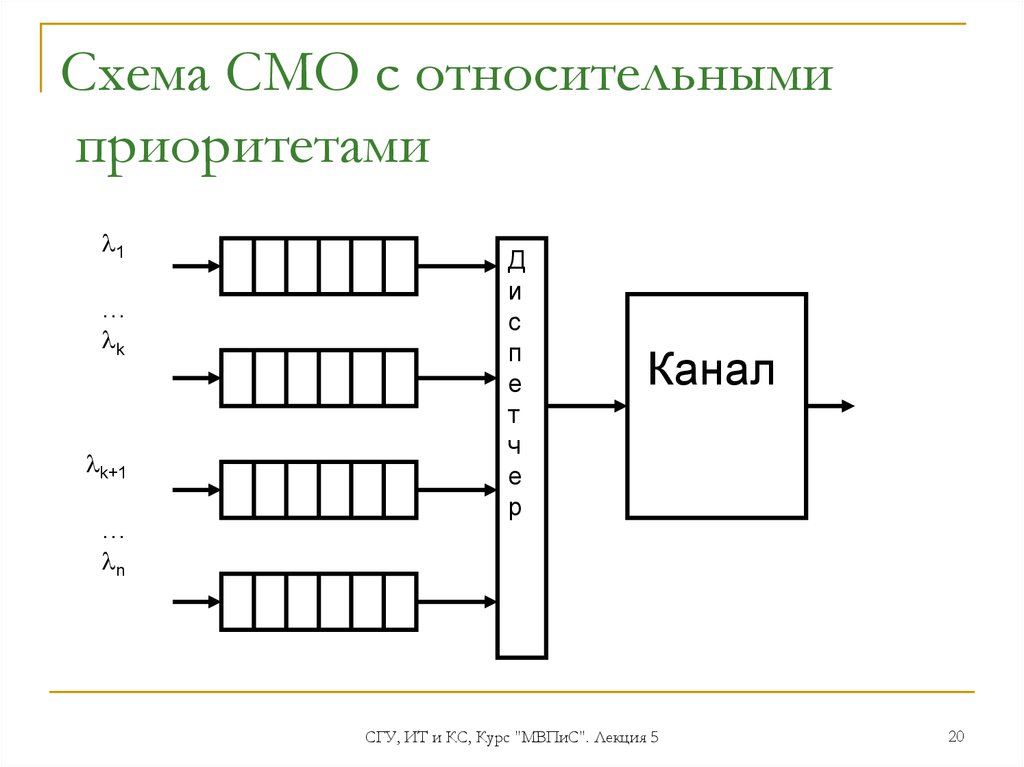
20. Схема СМО с относительными приоритетами

1
…
k
k+1
…
n
Д
и
с
п
е
т
ч
е
р
Канал
СГУ, ИТ и КС, Курс "МВПиС". Лекция 5
20

21.

в СМО поступают N простейших потоков с
интенсивностями 1 ,…, n
времена обслуживания – случайные
величины с известными средними Ƭ1 ,…,
Ƭn
и вторыми начальными моментами
Ƭ1(2) ,…, Ƭn(2)
дисциплина
обслуживания
–
относительные приоритеты
Определим среднее время пребывания в
очереди wk заявки k-го приоритета в
стационарном режиме.
СГУ, ИТ и КС, Курс "МВПиС". Лекция 5
21

22.

В
некоторый момент времени в СМО
поступает заявка k-го приоритета. Тогда она
ждет в очереди случайное время Wk:
k
k 1
j 1
j 1
Wk T0 T j T j ,
*
где То – время дообслуживания заявки;
k
T
j
– длительность обслуживания заявок
данного и более высоких приоритетов,
поступивших в СМО ранее данной заявки;
j 1
СГУ, ИТ и КС, Курс "МВПиС". Лекция 5
22

23.

k 1
Tj
*
– длительность обслуживания
j 1
заявок
более высоких приоритетов,
поступивших в СМО позже данной заявки
за время wk, которые будут обслужены
ранее данной заявки.
Для средних времен имеем:
___
__
k
__
k 1 __
W k T0 T j T j
j 1
СГУ, ИТ и КС, Курс "МВПиС". Лекция 5
*
j 1
23

24.

__
W w;
Обозначим:
__
*
j
Тогда:
T
j wk
__
T j j w j j j w j ,
___
__
k
k 1
j 1
j 1
W k T0 j w j j wk , (1)
СГУ, ИТ и КС, Курс "МВПиС". Лекция 5
24

25.

N
1
( 2)
Wk
i i (2)
2(1 Rk 1 )(1 Rk ) i 1
где
Rk = 1 + 2 + … + k; Rk = R.
Остальные характеристики вычисляются по
формулам:
nk uk k
Lk Wk k uk Wk k
СГУ, ИТ и КС, Курс "МВПиС". Лекция 5
25

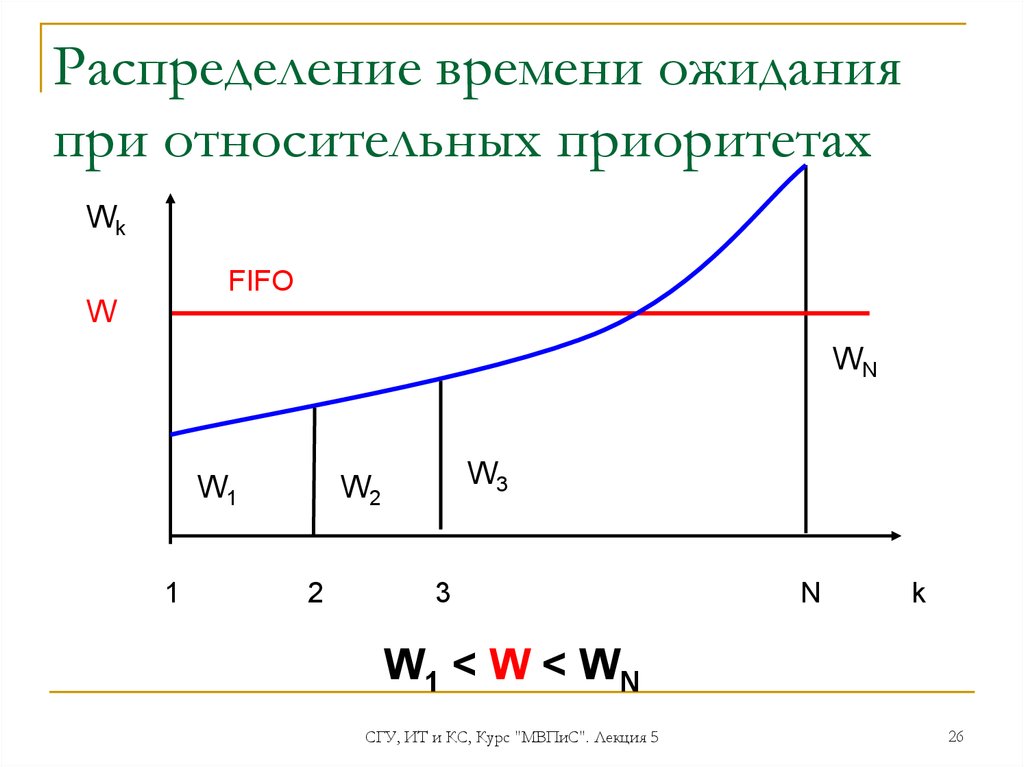
26. Распределение времени ожидания при относительных приоритетах

Wk
FIFO
W
WN
W1
1
W3
W2
2
3
N
k
W1 < W < WN
СГУ, ИТ и КС, Курс "МВПиС". Лекция 5
26

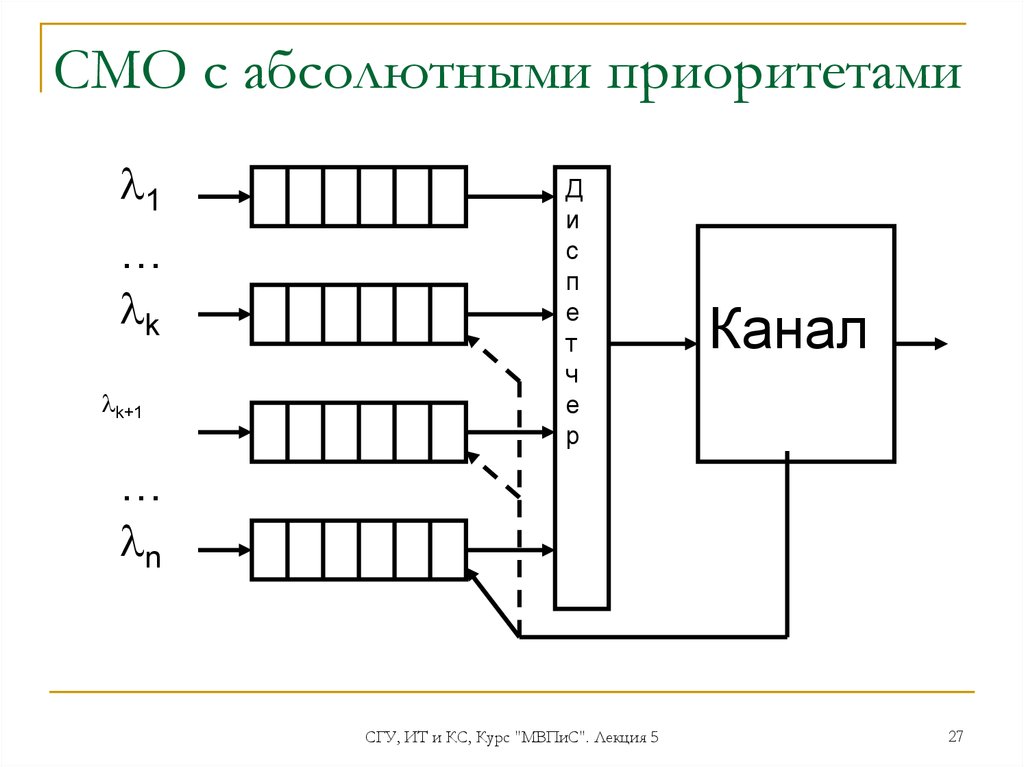
27. СМО с абсолютными приоритетами

1
…
k
k+1
Д
и
с
п
е
т
ч
е
р
Канал
…
n
СГУ, ИТ и КС, Курс "МВПиС". Лекция 5
27

28. Обслуживание с абсолютными приоритетами

обслуживающий канал занят обслуживанием
заявки k-го приоритета;
на вход системы поступает заявка j-го
приоритета;
при k j (у прибывшей заявки более низкий
или такой же приоритет) заявка j-го приоритета
заносится в конец соответствующей очереди;
СГУ, ИТ и КС, Курс "МВПиС". Лекция 5
28

29. Обслуживание с абсолютными приоритетами

при k > j (у прибывшей заявки более высокий
приоритет) – обслуживание заявки
k-го
приоритета прерывается;
прерванная заявка заносится в начало
очереди
k-го
приоритета
и диспетчер
переключает канал на обслуживание заявки jго приоритета.
СГУ, ИТ и КС, Курс "МВПиС". Лекция 5
29

30. Организация обслуживания с абсолютными приоритетами

Обслуживание прерванных заявок может
производиться:
1) от начала обслуживания
2) от момента прерывания
(дообслуживание).
СГУ, ИТ и КС, Курс "МВПиС". Лекция 5
30

31.

Среднее время ожидания в очереди wk заявок
k-го приоритета равно:
WkA = WkН + WkП
где WkН – среднее время ожидания начала
обслуживания
WkП – среднее время ожидания в прерванном
состоянии
N
Wk
А
( 2)
Rk 1 k
(3)
2(1 Rk 1 )(1 Rk ) 1 Rk 1
i 1
i i
СГУ, ИТ и КС, Курс "МВПиС". Лекция 5
31

32. Разность длительностей ожидания заявок k-го приоритета

N
( 2)
i i
R
A
O
i k 1
Wk W k W k k 1 k
1 Rk 1 2(1 Rk 1 )(1 Rk )
первое слагаемое определяет влияние заявок
более высокого приоритета, прерывающих
обслуживание данного потока,
второе учитывает уменьшение времени
ожидания заявок
k-го приоритета за счет
прерываний обслуживания заявок с меньшими
приоритетами.
СГУ, ИТ и КС, Курс "МВПиС". Лекция 5
32

33. Условие, при котором абсолютные приоритеты дают выигрыш во времени ожидания

Для заявок k-го приоритета
WkA < WkO ( Wk < 0)
N
Rk 1 k (1 Rk )
i k 1
СГУ, ИТ и КС, Курс "МВПиС". Лекция 5
i
( 2)
i
2
33

34. Распределение времени ожидания при абсолютных приоритетах

Wk
FIFO
W
WN
ОП
W1
АП
1
W3
W2
2
3
СГУ, ИТ и КС, Курс "МВПиС". Лекция 5
N
k
34

35.

Закон сохранения времени ожидания
справедлив
для
СМО,
следующим требованиям:
удовлетворяющих
1.Отсутствие отказов в обслуживании
2.Все
входные
потоки
независимые
и
простейшие
3.Система обслуживания простаивает только в
том случае, когда на ее входе нет заявок на
обслуживание
СГУ, ИТ и КС, Курс "МВПиС". Лекция 5
35

36.

Закон сохранения времени ожидания
4.Время обслуживания не зависит от входных
потоков
5.При наличии прерываний время обслуживания
имеет экспоненциальное распределение.
Применение:
для оценки достоверности приближенных
результатов, полученных при анализе сложных
дисциплин
обслуживания
и
проведении
имитационного моделирования.
СГУ, ИТ и КС, Курс "МВПиС". Лекция 5
36

37.

Закон сохранения времени ожидания
N
i wi const
i 1
при любой дисциплине
обслуживания
N
R
( 2)
соnst
i i
2(1 R) i 1
где R = 1 + 2 + … + N.
СГУ, ИТ и КС, Курс "МВПиС". Лекция 5
37

38. СМО со смешанными приоритетами

В одноканальную СМО поступают N потоков
заявок. Выделяются три группы потоков:
1)
N1 первых потоков имеют абсолютные
приоритеты
2)
потоки N1 + 1, …, N1 + N2 относительные приоритеты
3)
потоки N1 + N2 + 1, …, N –
бесприоритетное обслуживание.
СГУ, ИТ и КС, Курс "МВПиС". Лекция 5
38

39. Среднее время ожидания в очереди заявок k-го приоритета

K
( 2)
i i
R
k 1 k
i 1
k 1...N1
1 Rk 1 2(1 Rk 1 )(1 Rk )
N
( 2)
i i
RN1 k
i 1
WK
k N1 1...N1 N 2
1 RN1 2(1 Rk 1 )(1 Rk )
N
( 2)
i i
R
N1 k
i 1
k N1 N 2 1...N
1 R
2(1 RM1 М 2 )(1 R)
N1
СГУ, ИТ и КС, Курс "МВПиС". Лекция 5
39

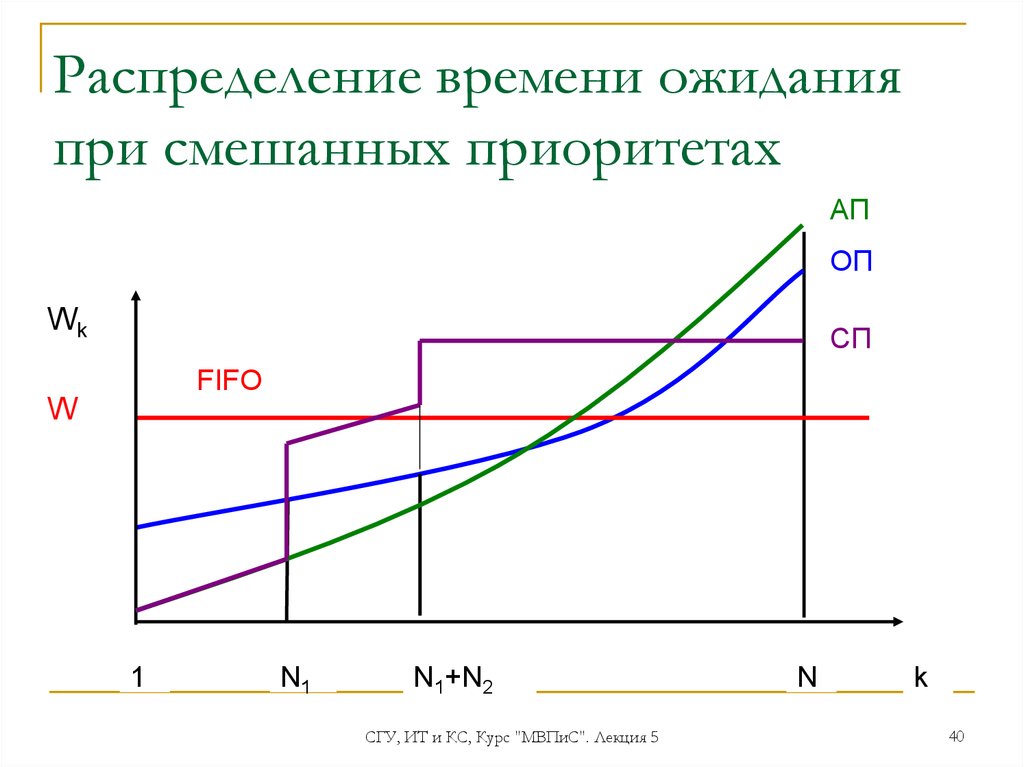
40. Распределение времени ожидания при смешанных приоритетах

АП
ОП
Wk
CП
FIFO
W
1
N1
N1+N2
СГУ, ИТ и КС, Курс "МВПиС". Лекция 5
N
k
40

41.

Спасибо за внимание!
СГУ, ИТ и КС, Курс "МВПиС". Лекция 5
41