Similar presentations:
Смеси идеальных газов. I закон термодинамики. Внутренняя энергия и работа
1. ТНиС 02
● Смеси идеальных газов● I закон термодинамики
● Внутренняя энергия и работа
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
1
2. Основное уравнение газов
Если в сосуде находится смесь идеальных газов, то еедавление можно найти по основному уравнению
молекулярно-кинетической теории газов, Па:
2 m1w12 2 m2 w22
p n1
n2
... ,
3
2
3
2
(1)
где n1, n2 – число молекул каждого газа в 1 м³ смеси;
w1, w2 – средние скорости движения молекул газов, м/с.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
2
3. Закон Дальтона
Каждая составляющая в уравнении (1) представляетсобой парциальное давление pi компонента смеси, то есть
давление, которое имел бы компонент, если бы он один
занимал весь объем смеси.
Тогда закон Дальтона для смеси газов при n компонентах
имеет вид:
n
p pi
.
(2)
1
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
3
4. Смеси идеальных газов
В технике часто приходится иметь дело со смесями газов(продукты сгорания топлива в ПТУ, ГТУ, ДВС).
Воздух также является смесью газов: N2, O2, H2O, CO2.
Смесью газов считается механическая смесь компонентов,
не взаимодействующих между собой химически.
Каждый компонент занимает весь объем смеси, имеет
температуру смеси и свое парциальное давление.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
4
5. Массовая и объемная доли компонента
Смесь можно задать массовыми, объемными и мольнымидолями компонентов:
● массовая доля – отношение масс компонента и смеси:
gi=mi/m.
n
gi 1 .
1
1
Так как mi m , то
n
● объемная доля – это отношение парциального объема
компонента к объему смеси:
ri=Vi /V.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
5
6. Объемная доля компонента
Парциальный объем компонента – это объем, которыйимел бы один газ при полном давлении смеси.
При T=idem по закону Бойля-Мариотта pVi=piV,
откуда парциальный объем компонента
Vi=Vpi /p.
(3)
n
n
По закону Дальтона pi p , тогда из (3): Vi V ,
1
1
то есть сумма парциальных объемов компонентов
равна объему смеси, следовательно:
n
ri 1
.
(4)
1
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
6
7. Мольная доля компонента
Обозначим число кило молей компонента и смесисоответственно Mi, M.
● Мольная доля – отношение числа кило молей компонента и
смеси Mi/M. С учетом того, что Mi=mi/μi; M=m/μ, получим:
M i mi iVi
.
M m i V i
По закону Авогадро при p=idem; T=idem: ρi/ρ = μi/μ.
Подставив (6) в (5), получим
(5)
(6)
M i Vi
ri , то есть
M V
задания смеси мольными и объемными долями равнозначны.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
7
8. Молекулярная масса смеси
Масса смеси равна сумме масс ее компонентовС учетом того, что m=μM; mi=μiMi, получим:
n
m mi
.
1
mi i M i i ri
gi
.
m M
Поделив на M левую и правую части полученного равенства
и с учетом обозначения мольной доли ri=Mi/M имеем:
n
( i ri ),
(7)
1
то есть кажущаяся молекулярная масса смеси равна сумме
произведений молекулярных масс компонентов на их
мольные (объемные) доли.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
8
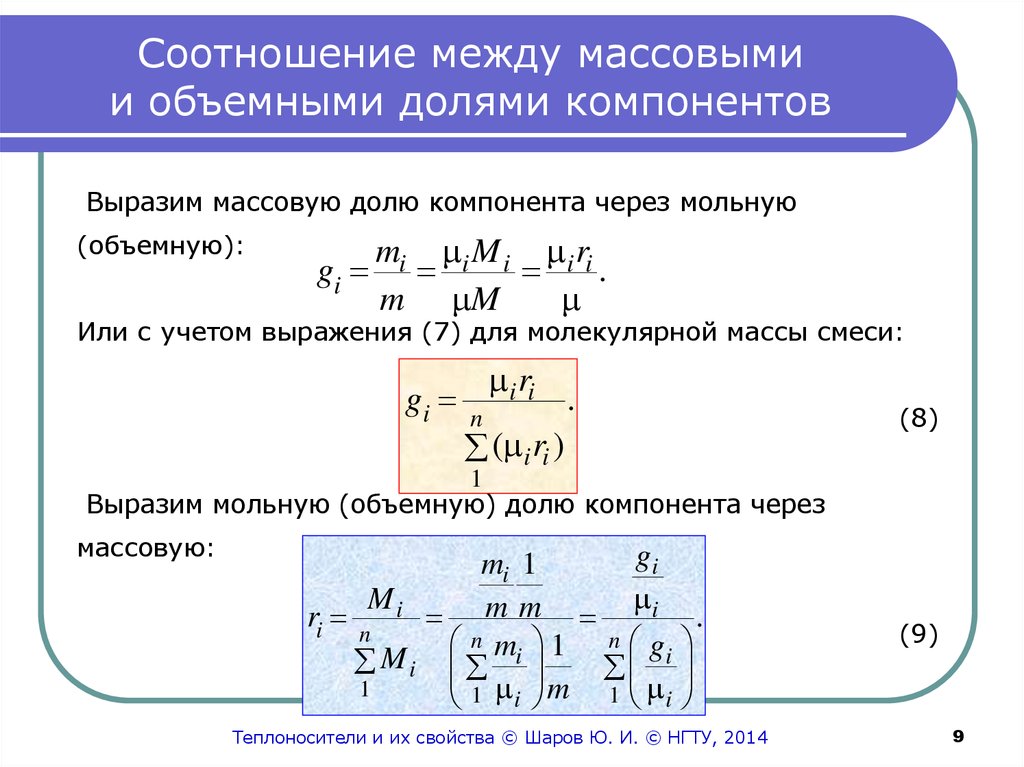
9. Соотношение между массовыми и объемными долями компонентов
Выразим массовую долю компонента через мольную(объемную):
gi
mi i M i i ri
.
m M
Или с учетом выражения (7) для молекулярной массы смеси:
gi
i ri
n
.
( i ri )
(8)
1
Выразим мольную (объемную) долю компонента через
массовую:
gi
mi 1
Mi
i
m
m
ri n
.
n
n
M i mi 1 gi
1
1 i m 1 i
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
(9)
9
10. Уравнение Клапейрона
Запишем уравнение состояния идеальных газов(Клапейрона) для смеси и компонента:
pV = mRT;
piV = miRiT.
(10)
Просуммируем левые и правые части последнего:
n
n
( pi )V [ (mi Ri )]T
1
n
.
1
Но по закону Дальтона pi p ,
1
с учетом чего имеем:
n
pV [ (mi Ri )]T .
(11)
1
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
10
11. Газовая постоянная смеси
При сравнении (10) и (11) видим, что их левые частиодинаковые, значит и правые части равны между собой:
n
mR (mi Ri ) , откуда поделив на m и с учетом mi /m=gi
1
имеем:
n
R ( gi Ri ) .
(12)
1
Для определения газовой постоянной газов использовалась
формула R=8314/μ.
Ее можно использовать и для смеси газов, если подставить
в нее выражение молекулярной массы смеси, то есть:
R
8314
n
.
( i ri )
(13)
1
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
11
12. Парциальные давления компонентов
Чтобы определить парциальные давления компонентов,запишем уравнение Клапейрона для компонента и смеси:
piV=miRiT;
pV=mRT.
Поделим их левые и правые части pi/p=miRi/(mR)
и с учетом mi/m=gi получим:
p pg R / R .
i
i
(14)
i
или через объемные доли из закона Бойля-Мариотта piV=pVi:
pi pVi /V pri .
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
(15)
12
13. Параметр состояния – внутренняя энергия
Внутренняя энергия газа u, Дж/кг:представляет собой сумму кинетических энергий
поступательного и вращательного движения молекул,
колебательного движения атомов в молекуле и
потенциальной энергии взаимодействия
между молекулами:
u E
ï î ñò
êèí
Eêèí E
âðàù
êî ëåá
êèí
3
Eï î ò Eêèí Eï î ò
.
1
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
13
14. Функция процесса – теплота
При соприкосновении двух тел они обмениваются внутреннейэнергией в форме теплоты q, Дж/кг (процесс теплообмена
между телами).
Таким образом, понятие теплоты относится к процессу
изменения состояния, в то время как параметр состояния
внутренняя энергия – только к состоянию рабочего тела.
Теплота, подведенная к газу – положительная;
отведенная от газа – отрицательная.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
14
15. Работа газа
dSПусть в цилиндре находится
1 кг газа при давлении p>pатм.
1 кг
p
1(p1,v1)
2(p2,v2)
4
0
3
dv
Газ стремится расшириться и
перемещает поршень, то есть
совершает положительную
работу + l, Дж/кг.
v
При сжатии над газом
совершается отрицательная
работа – l.
Работа, как и теплота является функцией процесса.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
15
16. Физический смысл pv-диаграммы
Заштрихованная площадка под процессом расширения1-2 является элементарной работой 1 кг газа
dl =pfdS=pdv,
где
p – давление, Па;
v - удельный объем газа, м3/кг;
f – сечение поршня, м²;
dS – перемещение поршня, м.
Работа газа в процессе 1-2, Дж/кг:
v2
l
pdv ï ë.12341
.
v1
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
16
17. I закон термодинамики
I закон (начало) термодинамики является частным случаемвсеобщего закона сохранения энергии М.В. Ломоносова.
Его аналитическое выражение вытекает из рассуждений:
если к 1 кг газа в цилиндре подвести теплоту dq, то его
температура возрастет на dT.
Следовательно внутренняя энергия газа изменится на
величину du.
Объем увеличится и газ переместит поршень на величину
dS, то есть совершит работу против внешних сил dl=pdv.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
17
18. Аналитическое выражение I закона термодинамики
Таким образом, аналитическое выражение I законатермодинамики для элементарного процесса:
dq=du+dl
или
dq=du+pdv
и для конечного процесса 1-2:
q=Δu+l.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
18

















 physics
physics








