Неклассические логики. (Глава 6)

ТРЕХЗНАЧНЫЕ ЛОГИКИ
Трёхзначная логика Лукасевича
0
x=
1
0
x = 1/ 2
1
Nx=1–x,
x & y = min ( x, y),
x y = max ( x, y),
x y = min ( 1, 1– x + y ).
N ( x & y ) = 1 - min ( x, y ) = max ( 1 – x , 1 – y ) = ( N x ) ( N y ),
но: х ( N x ) не всегда истинно.
Трёхзначная логика Гейтинга. В двузначной логике являются
тавтологиями как x x, так и x x. Из предположения, что
тавтологией можно считать только формулу x x, Гейтинг
разработал новую трёхзначную логику:
х y = min ( x, y ), x y = max ( x, y),
x y = 1, если x y,
x y = y, если x y.

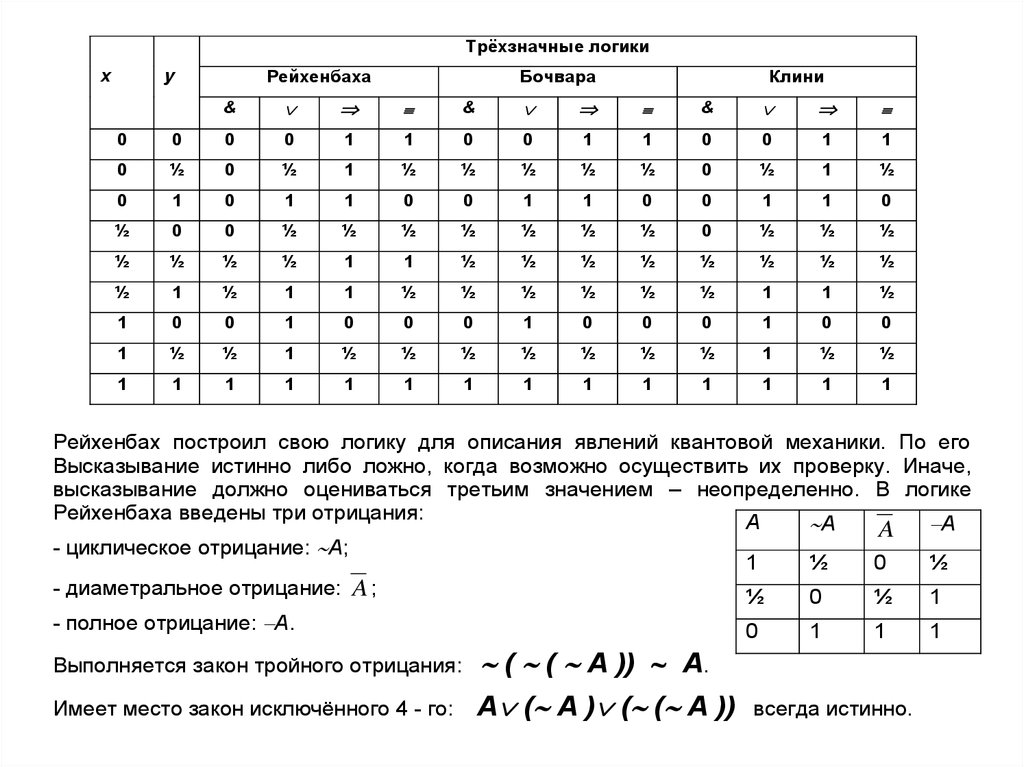
3.

Трёхзначные логики
х
у
Рейхенбаха
Бочвара
Клини
&
&
&
0
0
0
0
1
1
0
0
1
1
0
0
1
1
0
½
0
½
1
½
½
½
½
½
0
½
1
½
0
1
0
1
1
0
0
1
1
0
0
1
1
0
½
0
0
½
½
½
½
½
½
½
0
½
½
½
½
½
½
½
1
1
½
½
½
½
½
½
½
½
½
1
½
1
1
½
½
½
½
½
½
1
1
½
1
0
0
1
0
0
0
1
0
0
0
1
0
0
1
½
½
1
½
½
½
½
½
½
½
1
½
½
1
1
1
1
1
1
1
1
1
1
1
1
1
1
Рейхенбах построил свою логику для описания явлений квантовой механики. По его
Высказывание истинно либо ложно, когда возможно осуществить их проверку. Иначе,
высказывание должно оцениваться третьим значением – неопределенно. В логике
Рейхенбаха введены три отрицания:
А
А
A А
- циклическое отрицание: А;
1
½
0
½
- диаметральное отрицание: A ;
½
0
½
1
- полное отрицание: А.
0
Выполняется закон тройного отрицания:
( ( А )) А.
Имеет место закон исключённого 4 - го:
А ( А ) ( ( А ))
1
1
всегда истинно.
1

4.

КОНЕЧНОЗНАЧНАЯ ( K-ЗНАЧНАЯ, K 2 ) ЛОГИКА ПОСТА.
Переменная х может принимать значения: 0, 1 , 2 ,…, k - 1. Операции:
1)
2)
3)
4)
5)
6)
7)
8)
x = x + 1 ( mod k ) – цикл. отрицание или отрицание Поста;
Nx = k – 1 – x – отрицание Лукасевича;
k 1, если x m ,
I m( x ) =
m = 0 , 1 ,…, k - 1.
если x m ,
0,
х y = min ( x, y ) – конъюнкция;
x y = max ( x, y ) - дизъюнкция;
x y = x y ( mod k ) – произведение по модулю k;
x + y = x + y ( mod k ) – сумма по модулю k;
k 1,
x y=
( k 1) x y ,
если 0 x y k 1,
если 0 y x k 1.
Теорема. Число различных функций k - значной логики, зависящих от n
n
k
переменных, равно k
.
Теорема (о функциональной полноте, теорема А. В. Кузнецова). Для
каждой k - значной логики существует конечное число замкнутых
классов K 1 , K 2 , …, K r ( k ) таких, что для полноты системы функций k значной логики Ф = { 1 , 2 ,…, m } необходимо и достаточно, чтобы Ф
не содержалась целиком ни в одном из классов K 1 , K 2 , …, K r ( k ).

5.

МНОГОЗНАЧНАЯ ЛОГИКА ЛУКАСЕВИЧА
Переменная х может принимать одно из значений из Тk:
0
Тk = 0
,
k
1
1
,
k 1
k 2
2
, …,
,
k 1
k 1
k 1
1 .
k 1
(6.1)
Nx=1–x;
х y = min ( x , y );
(6.2)
x y = max ( x , y );
х y = min ( 1 , 1 + y - x ).
L 2, L 3, L 4, …
L - является бесконечнозначной логикой, для которой
истинностными значениями являются все рациональные числа
единичного отрезка [0,1], а операции вводятся по (6.2).
Логика, в которой истинностными значениями являются числа
из [ 0, 1 ], а операции вводятся по ( 6.2 ), считается стандартной
логикой Лукасевича – логикой L 1 .

6.

ПОНЯТИЕ НЕЧЕТКОГО ПОДМНОЖЕСТВА
1, если х А ,
Характеристическая функция подмн-ва А: А ( х ) =
0, если х А.
1
U = (- , ), А = [ - 2 , 3 ], тогда А(х) :.
Свойства характеристических функций:
1) А = В
х ( А ( х ) = В ( х ));
-2
0
3
2) С А ( х ) = 1- A ( х );
1,
3) μ А В ( х )
0,
1,
4) μ А В ( х )
0,
если х А В,
если х А В
если х А В,
если х А В
= min ( А ( х ), В ( х ));
= ma x ( А ( х ), В ( х )).
Нечеткое подмножество А* = { х , А* ( х ) }, где х U, А* ( х ) [0,1];
А* ( х ) - функция принадлежности, а U- универсальное множество.

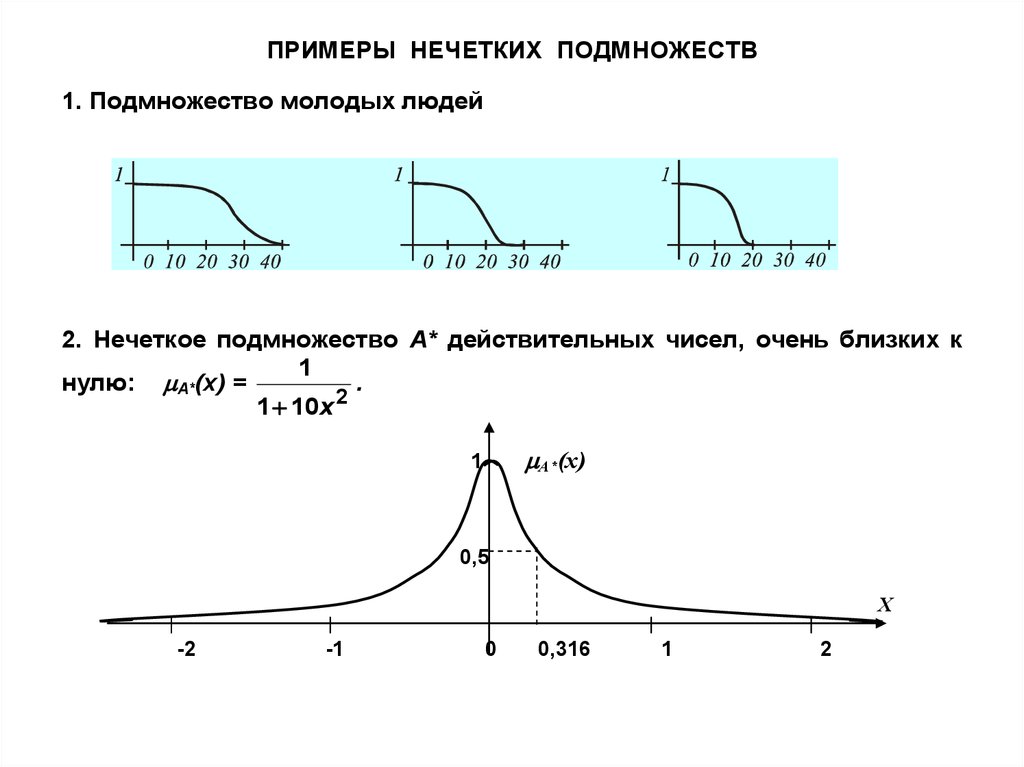
7.

ПРИМЕРЫ НЕЧЕТКИХ ПОДМНОЖЕСТВ
1. Подмножество молодых людей
2. Нечеткое подмножество А* действительных чисел, очень близких к
1
нулю: А*(х) =
.
2
1 10х
А*(х)
1
0,5
Х
-2
-1
0
0,316
1
2

8.

СООТНОШЕНИЯ ДЛЯ НЕЧЕТКИХ ПОДМНОЖЕСТВ
А* = В* х U : А* ( х ) = В* ( х ).
А* В*: х U : А* ( х ) В* ( х ),
х U : μ А ( х ) = 1- А* ( х )
х U : А* В* ( х ) = min ( А* ( х ), В* ( х )),
х U : А* В* ( х ) = mах ( А* ( х ), В* ( х )).
Пусть U = { u 1 , u 2 ,…, u n } и А* -
А* ( х ). Тогда:
А* = 1 / u 1 + 2 / u 2 +…+ n / u n ,
или
n
А * = μ i / ui .
i 1

9.

ЗАДАНИЕ НЕЧЕТКОГО ПОДМНОЖЕСТВА
ДЛЯ КОНЕЧНЫХ МНОЖЕСТВ
Пусть
U = { 5, 10, 20, 30, 40, 50, 60, 70, 80, 90 }.
Элементы
U ( годы )
5
10
20
30
40
50
60
70
80
90
из
Нечёткие подмножества
А*- молодой
В*- пожилой
старый
1
0
0
1
0
0
0,8
0,1
0
0,5
0,3
0,1
0,2
0,5
0,3
0,1
0,7
0,5
0
1
0,8
0
1
1
0
1
1
0
1
1
Нечёткое подмножество А* :
А* = 1/5 + 1/10 + 0,8/20 + 0,5/30 + 0,2/40 + 0,1/50.
В* = 0,1/20 + 0,3/30 + 0,5/40 + 0,7/50 + 1/60 + 1/70 + 1/80 + 1/90.
А* В* = 0,1/20 + 0,3/30 + 0,2/40 + 0,1/50.

10.

СВОЙСТВА ОПЕРАЦИЙ ДЛЯ НЕЧЕТКИХ ПОДМНОЖЕСТВ
Если А*, В*, и С* - нечеткие подмножества то:
1. А * = A* – инволютивность;
2. A* B* = B* A*
3. A* B* = B* A*
– коммутативность;
4. A* ( B* C* ) = ( A* B* ) C*
5. A* ( B* C* ) = ( A* B* ) C*
– ассоциативность;
6. A* ( B* C* ) = ( A* B* ) ( A* C* )
7. A* ( B* C* ) = ( A* B* ) ( A* C* )
– дистрибутивность;
8. A* = A*
9. A* U = U
10.A* =
11.A* U = A*
– свойства операций с и U;

11.

Свойства операций для нечетких подмножеств
Если А*, В*, и С* - нечеткие подмножества то:
…
A* B* = A* B*
– законы де Моргана;
A* B* = A* B*
A* A* = A*
A* A* = A*
– законы идемпотентности;
А* ( А* В* ) = А*
А* ( А* В* ) = А*
- законы поглощения.
Для мн-ва U U ( х ) = 1 при х U , для ( х ) = 0 для х U.
Но А* и В* такие, что:
A* A* U
и
В* В* .

12.

НЕЧЕТКАЯ ЛОГИКА
«Число 0,125 очень близко к нулю», «Волга - хорошая машина»,
«Молодая была уже не молода».
Для высказывания «Число 0,125 очень
1
близко к нулю» используем: А*(х) =
. Тогда при х = 0,125:
2
1 10х
А*(0,125)=
1
2
1 10 0.125
0.865.
Высказывания нечеткой логики : « х есть A* », где х U, A* – нечеткое
подмножество множества U. Полагаем: v ( A* ) = А* ( х ).
v ( А* ) = 1 – v ( А* )
v ( А* & В* ) = min ( v ( А* ), v ( В* ))
v ( А* В* ) = max ( v ( А* ), v ( В* ))
Или:
А* ( х ) = 1 - А* ( х );
А* & В* ( х ) = min ( А* ( х ), B* ( х ));
А* В* ( х ) = max ( А* ( х ), B* ( х ))

13.

ИЗОМОРФИЗМ АЛГЕБР
Структура
алгебры
Основное
множество
Выделенные
элементы из
основного
множества
Операции
А = U; , , - алгебра
подмножеств множества А
В = V; , &, алгебра высказываний
U – множество подмножеств V - множество
множества А
высказываний
П- противоречие
А
Т-тавтология
( ) – дополнение
- отрицание
- пересечение
& - конъюнкция
- объединение
- дизъюнкция
Существует изоморфизм между стандартной логикой Лукасевича L1
(с максиминными операциями) и алгеброй нечётких подмножеств с
операциями дополнения, пересечения и объединения.

14.

t - НОРМЫ И t – КОНОРМЫ
t – норма - бинарная операция t: [ 0, 1 ] [ 0, 1 ] [ 0, 1 ] :
1) коммутативности:
a t b = b t a;
2) ассоциативности:
( a t b ) t c = a t ( b t c );
3) монотонности:
если b c, то a t b a t c.
4) граничным условиям:
a t1 b = min ( a, b );
a t 1 = a; a t 0 = 0 a [ 0, 1 ].
a t2 b = a b;
a t3 b = max( 0, a + b – 1 ) – t – норма Лукасевича и …
t – конорма - бинарная операция s: [ 0, 1 ] [ 0, 1 ] [ 0, 1 ] :
1) коммутативности:
a s b = b s a;
2) ассоциативности:
( a s b ) s c = a s (b s c );
3) монотонности:
если b c, то a s b a s c.
4) граничным условиям:
a s1 b = max ( a, b );
a s 1 = a; a s 0 = 0 a [ 0, 1 ].
a s2 b = a + b – a b;
a s3 b = min ( a + b, 1 ) – t – конорма Лукасевича и …

15.

ИМПЛИКАЦИЯ НЕЧЕТКОЙ ЛОГИКИ
Существует > 40 вариантов нечеткой импликации:
импликация Лукасевича:
правило Мамдани:
А* В* ( х ) = max ( 1 - А* ( х ), B* ( х ));
А* В* ( х , y ) = min ( А* ( х ), B* ( y ));
ПОНЯТИЕ О НЕЧЕТКОЙ ЛИНГВИСТИЧЕСКОЙ ЛОГИКЕ
Лингвистической называется переменная, значениями которой
являются слова или предложения естеств. или искусственного языка.
(Х, Т(Х), U, G , М), где
Х - название лингвистической переменной,
Т(Х) - множество лингвистических значений переменной Х,
U - универсальное множество,
G - синтаксические правила, порождающие значения переменной,
т.е. правила определения лингвистических значений,
М - семантические правила, которые ставят в соответствие
каждому значению переменной ее смысл, т.е. характеристическую
функцию.

16.

ЛИНГВИСТИЧЕСКАЯ ПЕРЕМЕННАЯ «ВОЗРАСТ»
ВОЗРАСТ -лингвистическая перемен.
X
G(X)
очень молодой
T(X)
очень старый
молодой
1
M
U 0
10
20
30
70
111

17.

МОДАЛЬНЫЕ ЛОГИКИ
Модальности: «необходимость», «возможность», «доказано», «не
доказано», «запрещено», «разрешено», «всегда», «иногда» и т.п.
Модальные логики являются расширением обычной логики. В них
кроме , , , , , х и х вводятся операторы : и ◊ ( « p » «необходимо, что p » или « доказано, что p », или « разрешено p » ).
Модели Крипке
Р – множество (атомарных) высказываний.
Моделью Крипке над множеством Р высказываний наз-ся система:
M = (S,R,L), где
1) S - конечное множество состояний;
2) R - бинарное отношение переходов: для s S должно s* S,
что s R s* ;
3) L: S 2 P - функция, которая помечает каждое состояние
множеством атомарных высказываний, истинных в этом
состоянии.
Последовательность = s0 s1 s2 … - путь в модели Крипке из
состояния s0, если для всех i,
i 0, s i , s i+1 R .

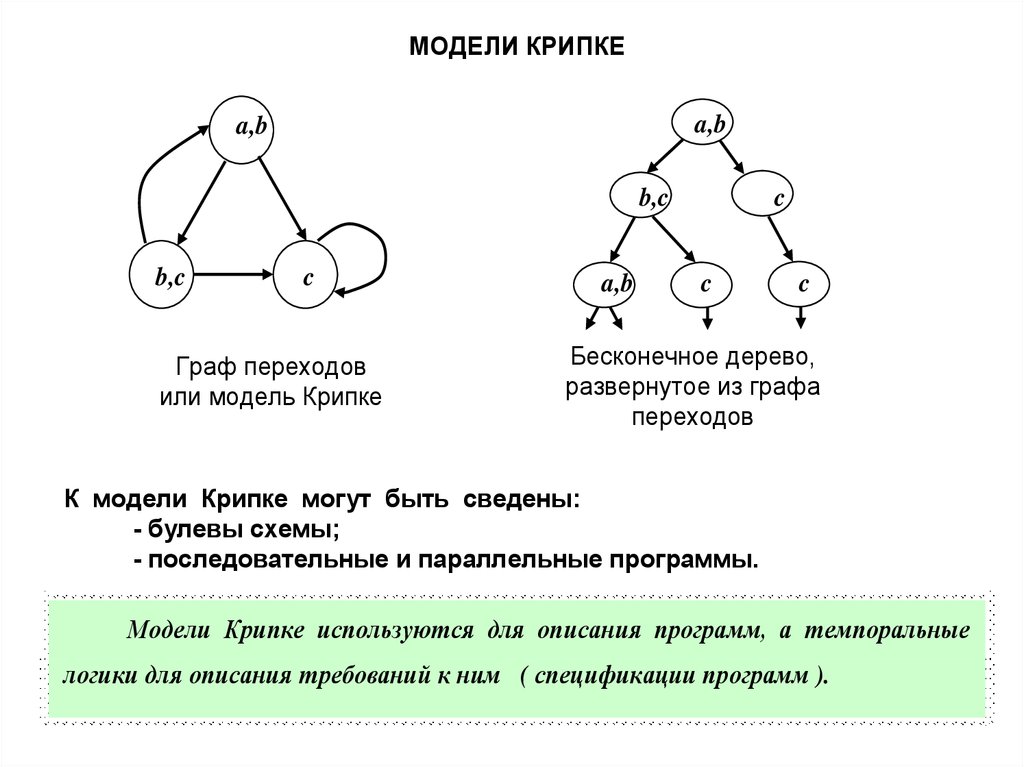
18.

МОДЕЛИ КРИПКЕ
a,b
a,b
b,c
b,c
c
Граф переходов
или модель Крипке
a,b
c
c
c
Бесконечное дерево,
развернутое из графа
переходов
К модели Крипке могут быть сведены:
- булевы схемы;
- последовательные и параллельные программы.
Модели Крипке используются для описания программ, а темпоральные
логики для описания требований к ним ( спецификации программ ).

19.

ВРЕМЕННЫЕ (ТЕМПОРАЛЬНЫЕ) ЛОГИКИ
Временные (темпоральные) логики вводят понятия «было»,
«есть», «будет» («раньше», «одновременно», «позже»).
Темпоральные логики являются модальными логиками, они
получаются добавлением к алгебре высказываний новых операторов
отражающих временные свойства.
Темпоральные логики классифицируются в соответствии с тем,
является ли структура времени линейной или ветвящейся.
Темпоральная логика деревьев вычислений CTL*
Обозначение CTL - «Computational Tree Logic».
Кванторы пути: A: «выполнено для всех путей ( вычислений )»;
E: «выполнено для некоторых путей (вычислений )».
Темпоральные операторы:
X: «в следующий момент времени» ;
G: «когда-то в будущем»;
F: «всегда, повсюду».

20.

ВРЕМЕННЫЕ ОПЕРАТОРЫ
U: - «до тех пор пока».;
R: - «высвободить».
Обозначения X, F, G, U, R получены из слов «neXttime», «Future»,
«Generally» («Globally»), «Until» и «Release» соответственно.
P множество (атомарных) высказываний.
Формулы состояния логики CTL*:
- если p P, то p - формула состояния (ф.с.);
- если f и g - ф.с., то f, f & g и f g - ф.с.;
- если f - формула пути, то E f и A f - ф.с..
Формула пути логики CTL*:
- если f - ф.с., то f - формула пути;
- если f и g - ф.с., то f, f & g, f g, X f, F f, G f, f U g, f R g – форм. пути.
Запись M , s ╞ f означает, что ф. с. f выполнена на модели M со
стартовой вершиной s.
Из десяти операторов , &, , A, E, X, F, G, U, R можно оставить:
например: , , E, X, U, а остальные выражаются через них:
f & g ( f g ); f R g ( f U g ); F f True U f; G f F f; Af E f.

21.

ТЕМПОРАЛЬНЫЕ ЛОГИКИ CTL И LTL
Логика деревьев вычислений CTL представляет собой фрагмент
CTL*, в которой темпоральный оператор X, F, G, U и R должен
следовать непосредственно за квантором пути, при этом формулы
пути определяются только одним условием:
если f и g - ф.с., то X f, F f, G f, f U g и f R g - формулы пути.
Линейная темпоральная логика LTL состоит из всех формул вида
A f, где f формула пути, в которой все формулы состояния – это
атомарные высказывания.
Типичными CTL формулами, возникающими при верификации
систем параллельных программ с конечным числом состояний, будут,
например, следующие:
EF ( Start & Ready ): можно достичь такого состояния, в котором
условие Start выполняется, а Ready - нет;
AG ( Req AF Ack ) : если получен запрос, то рано или поздно он
будет подтвержден;
AG ( EF Restart ): из состояния достижимо состояние Restart.

22.

ВЕРИФИКАЦИЯ ПРОГРАММ
Модели Крипке используются для описания программ.
Темпоральные логики для описания требований к ним ( спецификации
программ ).
Основная проблема эффективных алгоритмов верификации состоит в
экспоненциальном росте числа состояний в модели Крипке.
На начальном этапе системы верификации были способны проверять
5
системы, содержащие примерно 10 состояний. В настоящее время,
внесенные улучшения в технологию верификации, позволяют
расширить границы по числу состояний до
120
10 .

English Русский Rules