Similar presentations:
Логика предикатов. (Глава 2)
1.
Глава 2ЛОГИКА ПРЕДИКАТОВ
1
2.
Гл.1. Логика высказыванийВысказывания:
2 + 2 = 4, 2 > 5, Сегодня 1-ое апреля.
Не высказывания: sin x > 0, x y, x + y > z.
Данное предложение ложно.
Логические операции: , &, , , .
Логика предикатов
1. Понятие предиката
М – множество.
Предикат – повествовательное предложение, которое
при фиксировании переменных (замене их
элементами из М) становится высказыванием.
Предикаты: sin x > 0 - одна переменная (х);
x y
- две переменные (х,у);
x + y > z - три переменных (x,y,z);
2 + 2 = 4, 2 > 5, Сегодня 1-ое апреля - 0 переменных.
2
3.
ПРЕДИКАТПредикат – предложение, которое при фиксировании
переменных становится высказыванием.
Примеры:
sin x > 0,5
sin ( /2) > 0,5 - И,
sin ( ) > 0,5 - Л;
3
4.
ПРЕДИКАТПредикат – предложение, которое при фиксировании
переменных становится высказыванием.
Примеры: sin x > 0,5 sin ( /2) > 0,5 - И,
sin ( ) > 0,5 - Л;
х2 + у2 4 12 + 12 4 - И
32 + 32 4 - Л
0 1 2 3
Область истинности
n - местным предикатом Р(х1,х2,…,хn) на множестве M называется
n - аргументная функция отображающая M n в
{ И, Л }.
Р(х1,х2,…,хn): M M … M { И, Л }
4
5.
Пусть Р(x),Q(x) – одноместные предикаты на М.
Операции над предикатами:
Р(x) - одноместный предикат, значение которого при х = а,
а М, равно значению высказывания Р(а).
Р(x) & Q(x) -одноместный предикат, значение которого при х
= а, а М, равно значен. высказ. Р(а) & Q(а).
Р(x) Q(x), Р(x) Q(x) , Р(x) Q(x),
но
Р(x) & Q(y) - 2-х
R(x,y) Q(z) - 3-х
местн. предикат,
местн. предикат.
, &, , ,
5
6.
КВАНТОРЫX
Y
Пусть М – множество,
Р(х) – одноместный предикат.
хР(х) :
"для всех х (выполняется) Р(х)",
"для любого х Р(х)",
"для каждого х Р(х)".
" хР(х)" - высказывание истинное, когда Р(х) истинно для каждого х
из M и ложное - в противном случае.
х – квантор (все)общности.
6
7.
КВАНТОРЫX
хР(х) :
Y
Пусть М – множество,
Р(х) – одноместный предикат.
"существует х такое, что Р(х)",
"хотя бы для одного х Р(х)",
"для некоторого (некоторых) х Р(х)".
" хР(х)" - высказывание, которое истинно, если Р(х) = И хотя бы
для одного значения переменной х M, и ложно, если Р(х)= Л для
всех значений переменной х.
х - квантор существования.
7
8.
КВАНТОРЫхР(х) :
"для всех х (выполняется) Р(х)",
X Y
"для любого х Р(х)",
"для каждого х Р(х)".
" хР(х)" - высказывание истинное, когда Р(х) истинно для
каждого х из M и ложное - в противном случае.
х - квантор всеобщности.
хР(х) :
"существует х такое, что Р(х)",
"хотя бы для одного х Р(х)",
"для некоторого (некоторых) х Р(х)".
" хР(х)" - высказывание, которое истинно, если Р(х) = И хотя бы
для одного значения переменной х M, и ложно, если Р(х)= Л для
всех значений переменной х.
х - квантор существования.
8
9.
КВАНТОРЫ(А ) все S суть Р -
х(S(х) Р(х));
(Е ) все S суть не Р -
х(S(х) Р(х));
S
P
S
P
( I ) некоторые S суть Р - х(S(х) & Р(х));
(О ) некоторые S не суть Р - х(S(х) & Р(х)).
S
P
с квантором общности х используется связка ,
с квантором существования х - связка &.
M = { а1, а2,..., аn } и Р(х) - одноместный предикат на M. Тогда имеем:
х Р(х) Р(а1) & Р(а2) &...& Р(аn ),
х Р(х) Р(а1) Р(а2) ... Р(а n ).
9
10.
ПРИПИСЫВАНИЕ КВАНТОРОВ К МНОГОМЕСТНЫМ ПРЕДИКАТАМP(х1,х2,...,хn) - n-местный (n 2) предикат на множестве M. Тогда
хi Р(х1,х2,...,хn), 1 i n,
является (n-1) - местным предикатом, зависящим от переменных
х1,х2,...,хi-1,хi+1,...,хn, причем высказывание хiР(а1,а2,...,а i-1,х i,а i+1,...,а n)
истинно тогда и только тогда, когда для любого значения аi M истинно
высказывание Р(а1,а2,...,а i-1,ai,а i+1,...,а n).
10
11.
ПРИПИСЫВАНИЕ КВАНТОРОВ К МНОГОМЕСТНЫМ ПРЕДИКАТАМP(х1,х2,...,хn) - n-местный (n 2) предикат на множестве M. Тогда
хi Р(х1,х2,...,хn), 1 i n,
является (n-1) - местным предикатом, зависящим от переменных
х1,х2,...,х i-1,х i+1,...,х n, причем высказывание хi А(а1,а2,...,а i-1,х i,а i+1,...,а n)
истинно тогда и только тогда, когда существует такое значение аi, (аi M)
переменной хi, для которого высказывание А(а1,а2,...,а i-1,а i,а
i+1,...,а n)
истинно.
11
12.
ТЕРМЫа1, а2,. а3,..- предметные постоянные.
х1, х2, х3.,... - предметные переменные.
A in , i 1, n 0, - предикатные,
f in , i 1, n 1, - функциональные буквы.
Определение терма:
а) всякая предметная постоянная или переменная есть терм;
б) если f in - функциональная буква и t1,t2,...,tn - термы, то f in (t1,t2,...,tn)
есть терм;
в) выражение является термом только в том случае, если это следует
из правил а) и б).
Примеры: а, х1,
f 12 (х ,а), f 32 (а, f (у)).
1
2
12
13.
ФОРМУЛЫЭЛЕМЕНТАРНАЯ ФОРМУЛА
Если Ain - предикатная буква, а t1, t2,...,tn - термы, то
Ain (t1, t2,...,tn) - элементарная формула.
Примеры:
A10 ,
A12 (х1, а1),
A11 ( f11 (х)),
2
A23 (х, у, f 1 (а,х)).
13
14.
ФОРМУЛЫФормулы логики предикатов:
а) всякая элементарная формула есть формула;
б) если А и В - формулы и х - предметная переменная, то каждое из
выражений ( А), (А В), ( хА) и ( хА) есть формула;
в) выражение является формулой только в том случае, если это
следует из правил а) и б).
Примеры: ( A10 A12 (х,а)),
( х A12 (х, f 11 ( f 11 (х)))),
( х ( х A11 (а))).
В ( хА) и ( хА) А область действия х и х соответ-но.
Упрощения в записях аналогично алг. высказ.
,
&, ,
х
х
, .
14
15.
СВОБОДНЫЕ И СВЯЗАННЫЕ ПЕРЕМЕННЫЕВхождение переменной
х
в данную формулу Ф называется
связанным, если х является переменной кванторов х, х из Ф или
находится в области действия входящих в Ф кванторов х, х; в
противном случае вхождение переменной
х
в Ф называется
свободным.
свободные вхождения
хА(х,у) А(х,у) ;
z( xP(х,z) Q(z,x,у) )
связанные вхождения
Переменная называется свободной (связанной) переменной в формуле
Ф, если существуют свободные (связанные) ее вхождения в Ф.
х( уР(х,у) Q(x,x)) – замкнутая формула,
хP(х,у) - незамкнутая, ибо содержит свободную переменную у.
15
16.
СВЯЗАННЫЕ ПЕРЕМЕННЫЕх ( х А (х) В (х) )
program Main;
var X: Integer;
procedure A;
var X: Integer;
begin
X:=1; writeln(X)
end;
procedure B;
begin
writeln(X)
end;
begin
X:=5; A; B
end.
16
17.
ИНТЕРПРЕТАЦИЯ ФОРМУЛИнтерпретация заданна, если:
1. Задано непустое
интерпретации.
множество
M,
называемое
областью
2. Заданы соответствия:
a) предикатным буквам Ain n - местные предикаты в M;
b) функциональным буквам f in функции из M n в M;
c) каждой предметной постоянной а фиксированный
элемент из M;
d) символам , , x, x обычный смысл.
3. Считается, что предметные переменные
всевозможные значения из M.
I = (M, { Pin }, { in }, {ai})
принимают
17
18.
ПРИМЕР ИНТЕРПРЕТАЦИИ ФОРМУЛЫА = x A13 ( x, y, b1 )
1)
M = [0, );
b1 1,
Тогда А: x(x + y 1) = Р(у).
A13 (x,y,z) x + y z.
Если 0 у < 1, то Р(у) = Л,
если у 1, то Р(у) = И.
I1 = ( [0, ); {x + y z}; ; {1} )
18
19.
ПРИМЕР ИНТЕРПРЕТАЦИИ ФОРМУЛЫА = x A13 ( x, y, b1 )
1)
I1 = ( [0, ); {x + y z}; ; {1} )
Тогда А: x(x + y 1) = Р(у).
Если 0 у < 1, то Р(у) = Л,
если у 1,
2)
I2 = ( [0, ); {x + y z}; ; {0} )
Тогда А: x(x + y 0) = Q(у).
3)
то Р(у) = И.
Q(у) = И при у из M.
I3 = ( [0, ); {x + y < z}; ; {0} )
Тогда А: x(x + y < 0) = R(у).
R(у) = Л при у из M.
19
20.
ФОРМУЛЫ ВЫПОЛИМЫЕ, ИСТИННЫЕ И ЛОЖНЫЕВ ДАННОЙ ИНТЕРПРЕТАЦИИ
Формула А называется выполнимой в данной интерпретации, если
она принимает значение И хотя бы для одной совокупности возможных
значений её свободных переменных. Если А не содержит свободных
переменных, то она выполнима, если принимает значение И в этой
интерпретации.
Формула А называется истинной в данной интерпретации, если она
принимает значение И для всех возможных значений её свободных
переменных. Если А не содержит свободных переменных, то А истинна,
когда она принимает значение И в этой интерпретации.
Формула А называется ложной в данной интерпретации, если она
принимает значение Л для всех возможных значений её свободных
переменных. Если А не содержит свободных переменных, то А ложна,
когда она принимает значение Л в этой интерпретации.
Данная интерпретация называется
моделью для
множества формул G, если каждая формула из G истинна в
этой интерпретации.
20
21.
ЛОГИЧЕСКИ ОБЩЕЗНАЧИМЫЕ, ВЫПОЛНИМЫЕ ИРАВНОСИЛЬНЫЕ ФОРМУЛЫ
Формула логики предикатов называется логически общезначимой,
если она истинна в любой интерпретации.
A A, xA xA, A A.
╞ А - А является логически общезначимой формулой.
Формула логики предикатов называется выполнимой, если существует
интерпретация, в которой она выполнима.
xA(x,y,b1) - выполнима.
Формула логики предикатов называется противоречием, если она
ложна во всякой интерпретации.
A& A,
A A.
21
22.
РАВНОСИЛЬНЫЕ ФОРМУЛЫА╞ В - « из А логически следует В »
Формулы A и B логики предикатов наз-ся равносильными
( A В ) если каждая из них логически влечет другую.
A В
А╞ В & B╞ A.
╞ А - « А логически общезначимая формула »
Теорема 2.1. A╞ B тогда и только тогда, когда ╞ A B.
Теорема 2.2. A В тогда и только тогда, когда ╞ A B.
А1, А2,…,Аm╞ В - « из А1, А2, …, Аn логически следует B »
22
23.
Перенесение отрицания через кванторы.Пусть M ={a1,a2,...,an}. Тогда:
хР(х) равносильно Р(а1)&Р(а2)&...&Р(аn),
хР(х) равносильно Р(а1) Р(а2) ... Р(а n).
хР(х)
(Р(а1) Р(а2) ... Р(аn)) Р(а1) Р(а2) ... Р(аn).
хР х
х Р х .
хР х
(Р а1 Р а2 ... Р аn Р а1 Р а2 ... Р аn ,
хР х х Р х .
х
х,у х 2 х,у
2
23
24.
ПЕРЕНЕСЕНИЕ ОТРИЦАНИЯ ЧЕРЕЗ КВАНТОРЫхА х А;
хА х А.
хА х А;
хА х А.
Теорема. Отрицание формулы, начинающейся с
кванторов, равносильно формуле, полученной заменой
каждого квантора на двойственный и перенесением знака
отрицания за кванторы.
х у z х у z
24
25.
ПРАВИЛА ПЕРЕСТАНОВКИ КВАНТОРОВОдноименные кванторы, стоящие рядом, можно переставлять
местами:
х у А
у х А
х у А
у х А.
Разноименные кванторы, можно переставлять не в формуле.
Теорема. Для каждой формулы А и предметных переменных х
и у формула
х у А у х А
(1)
логически общезначима, а формула
у х А х у А
(2)
не является логически общезначимой (при формуле А).
Для
произвольной
формулы
перестановка
разноименных
кванторов не всегда приводит к равносильным формулам.
25
26.
СВЯЗАННЫЕ ПЕРЕМЕННЫЕх ( х А (х) В (х) )
program Main;
var X: Integer;
procedure A;
var X: Integer;
begin
X:=1; writeln(X)
end;
procedure B;
begin
writeln(X)
end;
begin
X:=5; A; B
end.
26
27.
ПРАВИЛА ПЕРЕИМЕНОВАНИЯ ПЕРЕМЕННЫХхА(х) ~ уА(у).
1
1
cos x dx =
0
cos y dy.
0
m
m
xn / n2 =
n 1
x k / k2 .
k 1
Переименовываются только связанные переменные, но не
свободные.
хА(х) хВ(х) С(х)
уА(у) хВ(х) С(х)
хА(х) zВ(z) С(х)
yА(y) zВ(z) С(х)
Можно переименовывать связанные переменные на другие
отличные от всех переменных формулы А.
27
28.
ПРАВИЛА ВЫНЕСЕНИЯ КВАНТОРОВ ЗА СКОБКИТеорема 2.6:
А & хВ(х)
х(А & B(x)),
(2.23)
А хВ(х)
х(А B(x)),
(2.24)
А & хВ(х)
х(А & B(x)),
(2.25)
А хВ(х)
х(А B(x)),
(2.26)
( xB(x)) & xC(x)
( xB(x)) xC(x)
x(B(x) & C(x)),
x(B(x) C(x)).
Кроме того формулы
( xB(x)) xC(x) x(B(x) C(x)),
x(B(x) & C(x)) ( xB(x)) & xC(x)
(2.27)
(2.28)
(2.29)
(2.30)
логически общезначимы, а импликации, обратные к (2.29) и
(2.30), не являются логически общезначимыми.
28
29.
Правила вынесения кванторов за скобкиТеорема 2.7. Пусть А - произвольная формула,
не содержащая свободных вхождений переменой
х, а В(х)- произвольная формула. Тогда
хВ(х) А x(В(х) А);
(2.33)
А хВ(х) х(А В(х)),
(2.34)
хВ(х) А х(В(х) А),
(2.35)
А хВ(х) х(А В(х)).
(2.36)
29
30.
ПРАВИЛА ВЫНЕСЕНИЯ КВАНТОРОВ ЗА СКОБКИТеорема 2.8:
хВ(х) хС(х)
у z(B(y) C(z));
(2.38)
xB(x) xC(x)
x(B(x) C(x));
(2.39)
xB(x) xC(x)
y z(B(y) C(z));
(2.40)
xB(x) xC(x)
y z(B(y) C(z)),
(2.41)
где z и у - переменные, отличные от всех свободных
переменных формул В(х) и C(х).
30
31.
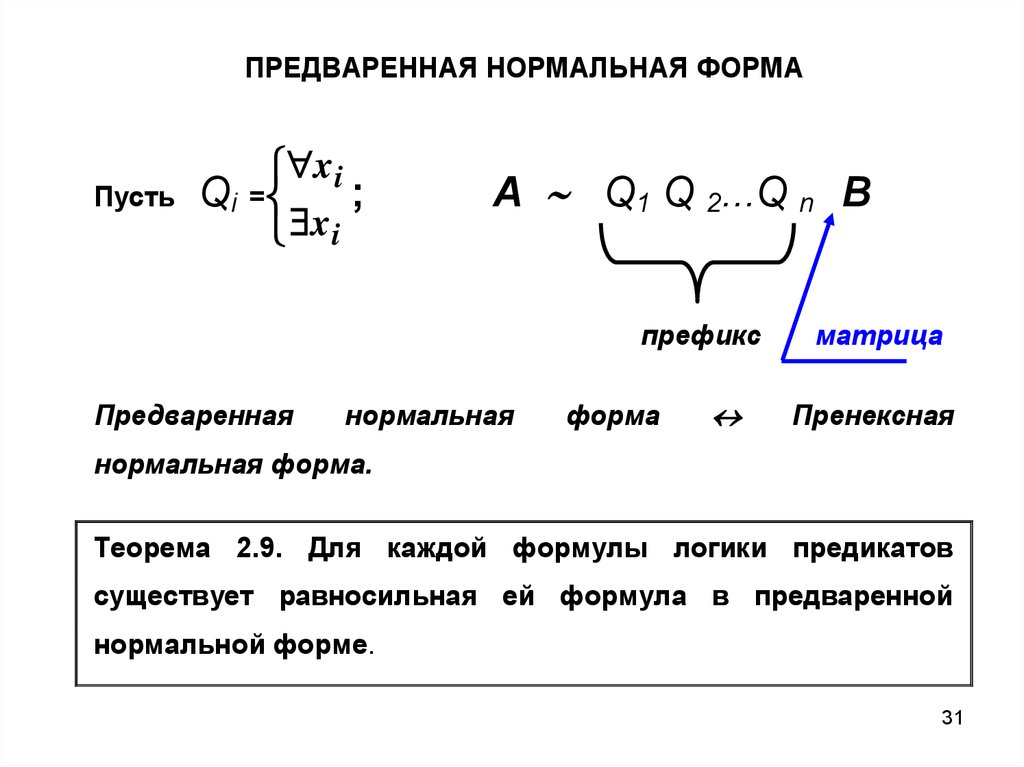
ПРЕДВАРЕННАЯ НОРМАЛЬНАЯ ФОРМАПусть
x i
Qi =
;
x i
А Q1 Q 2...Q n В
префикс
Предваренная
нормальная
форма
матрица
Пренексная
нормальная форма.
Теорема 2.9. Для каждой формулы логики предикатов
существует равносильная ей формула в предваренной
нормальной форме.
31
32.
ПРОБЛЕМА РАЗРЕШИМОСТИ ЛОГИКИ ПРЕДИКАТОВПроблема разрешимости логики предикатов: указать единый
способ (алгоритм), позволяющий для каждой формулы А за конечное
число действий выяснить, является ли А логически истинной или нет.
Имея такой способ, мы сможем узнавать, будет ли формула А выполнимой
или нет.
Если А логически общезначима, то А противоречие (логически ложна),
следовательно, А невыполнима. Если А не является логически общезначимой, то
А выполнима.
Теорема 2.10. Проблема разрешимости логики предикатов не
имеет решения.
32
33.
РАЗРЕШИМЫЕ СЛУЧАИ ПРОБЛЕМЫТеорема 2.11. Проблема разрешимости логики предикатов имеет
решение для формул, содержащих только нульместные или (и)
одноместные предикатные буквы.
Теорема 2.12. Проблема разрешимости логики предикатов имеет
решение для тех формул, предваренные нормальные формы которых
имеют вид:
х1 х2 … хk y1 y2 … ym B,
только хi
только yj
где B формула без кванторов.
33
34.
РАЗРЕШИМЫЕ СЛУЧАИ ПРОБЛЕМЫТеорема 2.12. Проблема выяснения логически общезначимости формул
ЛП разрешима для класса чистых формул, которые в предваренной
нормальной форме имеют префикс одного из следующих видов:
х1 х2 … хk y1 y2 … ym
х1 х2 … хk y z1 z2 … zm
х1 х2 … хk y1 y2 z1 z2 … zm.
Эти классы записывают аббревиатурами
* *, * *, * *
Следствие 2. . Проблема выяснения выполнимости формул ЛП
разрешима для класса чистых формул, которые в предваренной
нормальной форме имеют префикс одного из следующих видов:
* *,
* *,
* *
34
































 mathematics
mathematics








