Similar presentations:
Логика предикатов. ДМ.13
1. Дискретная математика
2. Предикаты
Предикат – это функциявида
Р(х1, х2, …, хn)=y,
Здесь х1, х2, …, хn предметные переменные; y
- значение предиката.
3. Предикаты
x1 M 1 , x2 M 2 , ..., xn M nгде M 1 , M 2 , ..., M n
предметные множества,
M 1 M 2 ... M n
поле предиката.
4. Предикаты
Переменная y – может приниматьзначения из множества
В={0, 1}.
Здесь 0 – «нет», «ложь»;
1 – «да», «истина».
5. Предикаты
Например:1) на множестве N задан предикат
Р(х) – «х является четным
числом».
Тогда Р(1)=0, Р(2)=1.
2) На множестве N×N задан
предикат Q(x,y) – «x≤y».
Тогда
Q(1,1)=1; Q(1,2)=1; Q(3,2) =0.
6. Предикаты
Подмножество I множества Мназывается областью
истинности предиката Р, если
наборы значений предметных
переменных из множества I
обращают предикат P в 1.
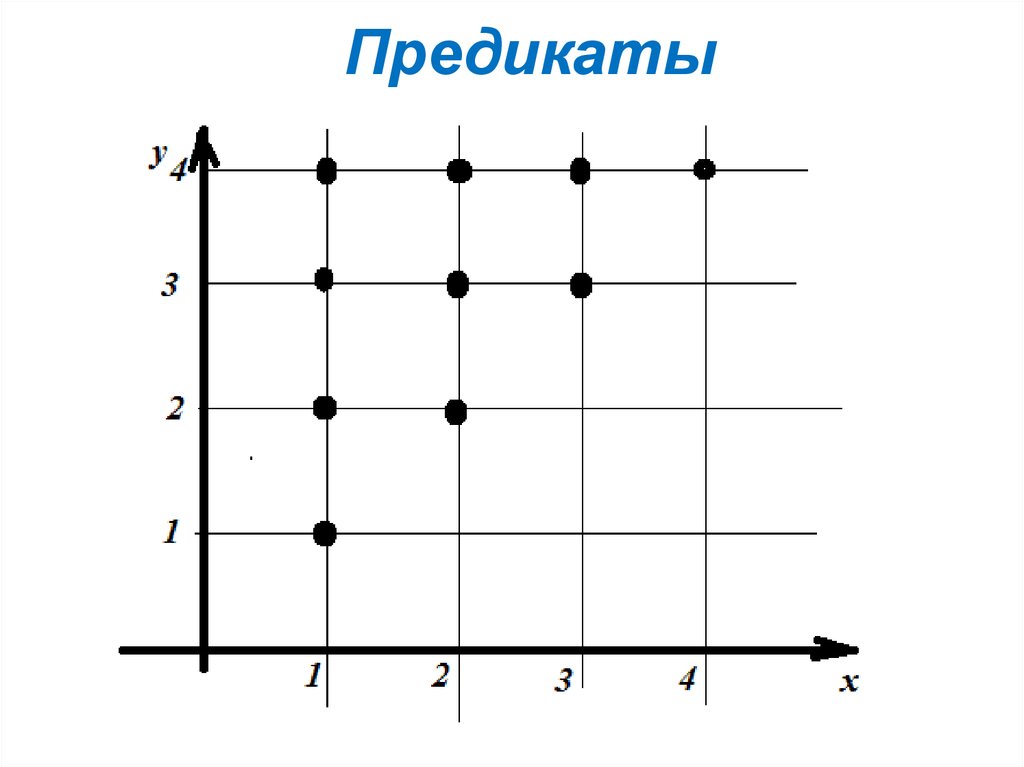
7. Предикаты
Например:Для предиката Q(x,y) область
истинности I – множество всех
точек плоскости с
натуральными координатами,
лежащие на диагонали
первого координатного угла и
выше.
8. Предикаты
9. Предикаты
Над предикатами можно совершатьзнакомые нам логические операции:
Конъюнкцию, дизъюнкцию,
отрицание, импликацию, и т. д.
Например:
Р(х,у) – «х<y», R(x,y) – «x=y».
Тогда ⌐ Р(х,у) – «х≥у»,
Р(х,у)V R(x,y) – «х≤у» и т. д.
10. Предикаты
При этом область истинностиполученных предикатов изменяется
по тем же правилам:
I P I P ;
I P R I P
и так далее.
IR;
11. Предикаты
Однако в логике предикатов естьоперация, которая отсутствуют в
логике высказываний.
Квантификация или квантирование
В результате этой операции на
переменную предиката навешивается
квантор (переменная связывается
квантором). Переменная при этом
становится связанной. Переменная,
не связанная называется свободной.
12. Предикаты
Существуют два видакванторов:
Квантор общности «для
любого, для каждого».
Квантор существования
«существует, найдется».
13. Предикаты
Предикатная формула:xP x
истинна тогда и только тогда,
когда предикат Р(х)=1 при
любом х,
ложна тогда и только тогда,
когда найдется х, при
котором предикат Р(х)=0.
14. Предикаты
Предикатная формула:xP x
истинна тогда и только тогда,
когда найдется х, при
котором предикат Р(х)=1,
ложна тогда и только тогда,
когда предикат Р(х)=0 при
любом х.
15. Замечание
Когда в предикате Р(х)переменная х связывается
квантором, она перестает влиять
на значение предиката и
предикат становится
высказыванием, принимающим
фиксированное значение
Истина или Ложь.
16. Предикаты
Например: Р(х) – «х являетсячетным числом» на множестве N
Тогда xP x 0
так как есть х=3, при котором
Р(3)=0.
Тогда xP x 1
так как есть х=2, при котором
Р(2)=1.
17. Предикаты
Если предикат имеет более 1переменной, то ее квантификация
приводит к уменьшению числа
переменных на 1.
Например:
предикат Q(x,y) – «x≤y» на
множестве N×N.
18. Предикаты
xQ x, y R( y )новый предикат от одной
переменной у – «любое
натуральное число х меньше либо
равно у».
При у=1 это не так (любой х ≤1) ,
xQ x,1 R(1) 0,
При у=2 это не так (любой х ≤2),
xQ x,2 R(2) 0,
19. Предикаты
Таким образом, предикатR( y) xQ x, y 0
то есть является функцией константой
20. Предикаты
xQ x, y W ( y)новый предикат от одной
переменной у – «найдется
натуральное число х меньше либо
равно у».
При у=1 это так (найдется х ≤ 1) ,
xQ x,1 W (1) 1,
При у=2 это так (найдется х ≤2),
xQ x,2 W (2) 1,
21. Предикаты
Таким образом, предикатW( y) xQ x, y 1
то есть тоже является функцией
-константой
22. Предикаты
Кванторы можно навесить на всепеременные предиката. Тогда
предикат станет высказыванием.
Например:
предикат Q(x,y) – «x≤y».
23. Предикаты
x yQ x, y 0так как неверно то, что любой
натуральный х меньше либо
равен любого натурального у.
Например, при х=5, у=2.
24. Предикаты
x yQ x, y 1так как верно то, что любой
натуральный х меньше либо
равен некоторого
натурального у.
Например, при х=1, у=1; при
х=2, у=2, …
25. Предикаты
y xQ x, y 0так как неверно то, что
найдется такой натуральный
у, который будет больше либо
равен любого натурального х.
Это связано с тем, что
натуральное множество не
ограничено сверху.
26. Предикаты
x yQ x, y 1так как верно то, что найдется
такой натуральный х,
который будет меньше либо
равен любого натурального у.
Этот х=1. Если бы неравенство
было строгое, высказывание
было бы ложным.
27. Предикаты
y xQ x, y 1так как верно то, что любой
натуральный у, больше либо
равен некоторого
натурального х.
Например, у=1, х=1;
у=2, х=2,…
28. Предикаты
x yQ x, y 1так как верно то, что найдутся
такие натуральные х и у, что
х меньше либо равен этого у.
Например х=3, у=7.
29. Логика предикатов
Логика предикатов, как илогика высказываний, – свод
правил, по которым строятся
формулы связывающие
простые предикаты в
предикатные формулы и
порядок определения
истинности/ложности этих
формул.
30. Логика предикатов
Равносильные предикатныеформулы – те, у которых
область истинности совпадает.
31. Логика предикатов
Интерпретация – этосопоставление каждому
предикатному символу в
формуле определенного
предиката.
32. Логика предикатов
Пусть формулы F и G содержатодно и тоже множество
свободных переменных.
Формулы F и G равносильны в
данной интерпретации –
если они выражают один и тот
же предикат.
33. Логика предикатов
Например:P x, y : x y; Q x, y : x y.
Тогда предикатные формулы:
F P x, y и G Q x, y
являются равносильными в данной
интерпретации, так как
P x, y Q x, y .
При других интерпретациях предикатов P и Q
формулы могут не быть равносильными.
34. Логика предикатов
Формулы F и G равносильнына множестве М – если они
равносильны во всех
интерпретациях на этом
множестве.
35. Логика предикатов
Например: F xP x , G xP xРавносильны в любой
интерпретации на множестве М,
если М состоит из одного
элемента. Если
a M : P a 0, xP x 0 и xP x 0.
Если
a M : P a 1, xP x 1 и xP x 1.
На другом множестве формулы F и G могут не
быть равносильными.
36. Логика предикатов
Формулы F и G равносильны влогике предикатов – если они
равносильны на всех
множествах.
37. Логика предикатов
Например:F P x P x ,
G P x P x .
Тогда F и G равносильны на любых
множествах и при любых
интерпретациях предиката P(x).
F G
38. Равносильные формулы
Для предикатных формулсохраняются все равносильности
(эквивалентности) алгебры логики.
Например, закон де Моргана:
P x Q x P x Q x
P x Q x P x Q x
39. Свойства операций над предикатами
Перенос квантора через отрицаниеxP x x P x
1
xP x x P x
2
Здесь и далее, знак равносильности ≡
заменен знаком равенства.
40. Свойства операций над предикатами
Вынос квантора за скобкиxP x Q x P x Q 3
xP x Q x P x Q 4
41. Свойства операций над предикатами
Вынос квантора за скобкиxP x Q x P x Q 5
xP x Q x P x Q 6
42. Свойства операций над предикатами
Закон коммутативности дляодноименных кванторов:
x yP x, y y xP x, y 7
x yP x, y y xP x, y 8
43. Свойства операций над предикатами
Коммутативность даетвозможность использовать более
краткую запись:
x y zP x, y,z x, y, zP x, y,z 9
x y zP x, y, z x, y, zP x, y, z 10
44. Равносильные формулы
Проверить равносильность формулы влогике предикатов, не так просто, как в
логике высказываний. Высказывание
может принимать значения 0 и 1.
Формула с 2 высказываниями
содержит 2² возможных значений, и так
далее.
Предикат имеет бесконечное
множество интерпретаций.
45. Истинность в логике предикатов
Предикатная формула Fназывается выполнимой
(непротиворечивой), если
существует интерпретация
входящих в нее предикатов, в
которой F принимает значение
истина. То есть ее область
истинности не пуста.
46. Истинность в логике предикатов
Предикатная формула Fназывается тождественно
истинной (общезначимой),
если при любой интерпретация
входящих в нее предикатов,
область истинности совпадает с
областью определения.
47. Истинность в логике предикатов
Предикатная формула Fназывается тождественно
ложной (противоречивой),
если при любой интерпретация
входящих в нее предикатов,
область истинности пуста.
48. Истинность в логике предикатов
Например:F P x P x 1
Тождественно истинная формула.
G P x P x 0
Тождественно ложная формула
49. Истинность в логике предикатов
Замечание 1Формула F – общезначима тогда и
только тогда, когда
¬F – противоречива.
Замечание 2
Формула F – выполнима тогда и
только тогда, когда
¬F – не является общезначимой.
50. Истинность в логике предикатов
Замечание 3Если F и G – равносильные
формулы в логике предикатов, то
формула
W=F~G
общезначима и выполняется
равенство:
I F IG
51. Истинность в логике предикатов
Замечание 4Если формула
W=F→G
общезначима, то выполняется:
I F IG
52. Истинность в логике предикатов
Замечание 5Если y не входит в формулу P(x),
то следующие формулы
являются общезначимыми:
xP x P y ;
P y xP x .
53. Истинность в логике предикатов
Квантор общности являетсяобобщением конъюнкции,
поэтому справедлива формула:
x P x Q x
11
xP x xQ x .
54. Истинность в логике предикатов
Квантор существованияявляется обобщением
дизъюнкции, поэтому
справедлива формула:
x P x Q x
12
xP x xQ x .
55. Истинность в логике предикатов
Замечание 6Если в формулах (11) и (12)
поменять местами кванторы, то
получаются выражения, истинные
лишь в одну сторону:
x P x Q x
13
xP x xQ x .
56. Истинность в логике предикатов
xP x xQ x14
x P x Q x .
В таких случаях говорят, что
левая часть утверждения более
сильная, чем правая.
57. Истинность в логике предикатов
В таком случае, надовоспользоваться правилом:
xP x yP y zP z tP t ...
xP x yP y zP z tP t ...
То есть, если переменная
связана квантором, то неважно,
как она называется.
58. Истинность в логике предикатов
В выражениях (13) и (14) надосделать замену переменной, после
чего воспользоваться формулами
(4) и (5):
xP x xQ x
xP x yQ y
15
x y P x Q y .
59. Истинность в логике предикатов
xP x xQ xxP x yQ y
x y P x Q y .
16
60. Префиксная нормальная форма
Префиксной нормальной формой(ПНФ) называется формула,
имеющая вид:
Q1 x1Q2 x2 ...Qn xn F
где Q1 , Q2 ,...Qn кванторы,
F – предикатная формула,
имеющая вид ДНФ.



























































 mathematics
mathematics








