Статистический анализ выборок. Числовые характеристики ряда.

1.Основные понятия математической статистики.

Основные понятия математической статистики.

2. Основные числовые характеристики выборки.

Основные числовые характеристики выборки

Доверительный интервал для нормально распределённой случайной величины

3. Нормальное распределение. Функция Гаусса. Гистограмма

Нормальное распределение (распределение Гаусса).

319.18K

Category: $mathematics$ mathematics

Статистический анализ выборок. Числовые характеристики ряда

1. Статистический анализ выборок. Числовые характеристики ряда.

Кафедра медицинской и биологической физики с курсом информатики
Лекции «Физика, математика»
Раздел 1. Основы математического анализа, биомеханика, акустика
Статистический анализ выборок.
Числовые характеристики ряда.
Вопросы:
1. Основные понятия математической
статистики.
2. Числовые характеристики выборки.
3. Нормальное распределение. Функция
Гаусса.
Доцент, к.б.н. – Цокова
Татьяна Николаевна
1

2.

Значение темы в системе знаний врача:
Работники здравоохранения поставляют основную массу
данных, на которых базируется медицинская статистика.
Поэтому им следует знать, как эти данные могут и
должны использоваться, для того чтобы, с одной стороны,
повысить уровень своей работы, а с другой - улучшить
организацию медицинской помощи в своей стране.
2

3. 1.Основные понятия математической статистики.

Выборочный метод –
изучение большой совокупности объектов
относительно некоторого количественного
признака Х производится по сравнительно
небольшому числу случайно отобранных
объектов.
3

4. Основные понятия математической статистики.

Множество всех возможных значений
(вариант)-x*i называется генеральной
совокупностью, а число N – объемом
генеральной совокупности.
Относительной частотой называется
отношение частоты ni к объему выборки n:
p*i = ni / n.

5. Основные понятия математической статистики.

Выборкой (x1, x2, . . ., xn)
называется совокупность значений СВ Х ,
полученной в результате n независимых
экспериментов.
(x1, x2, ..., xn) - простой статистический ряд.
5

6. Основные понятия математической статистики.

Объемом совокупности называется
количество объектов в
совокупности.
Объем выборки n, как правило,
значительно меньше объема N
генеральной совокупности: n N.
6

7. Основные понятия математической статистики.

Определение 1 Закон статистического
распределение
Х
Р(Х)
х1
р1
х2
р2
х3
р3
…
…
хn
рn
k
p1 p2 ... pk pi 1.
i 1
7

8. Основные понятия математической статистики.

Определение 2.
Математическим ожиданием дискретной
случайной величины Х называется сумма
произведений всех возможных значений
случайной величины на соответствующие
вероятности появления этих значений, т.е.
8

9. Математическое ожидание -

Математическое ожидание
центр распределения;
самое ожидаемое значение ряда, т.е.
вероятность его максимальная;
среднее значение дискретной
случайной величины, т.е.
M (X ) X
9

10. Основные понятия математической статистики.

Определение 3.
Математическое ожидание квадрата
отклонения случайной величины Х от её
математического ожидания называют
дисперсией случайной величины Х и
обозначают D(X), т.е.
10

11. Дисперсия-

Дисперсия
мера рассеивания значений
случайной величины от среднего
значения;
имеет размерность квадрата
случайной величины;
11

12. Основные понятия математической статистики.

Определение 4.
Среднее квадратическое отклонение
случайной величины, является
арифметическим корнем из дисперсии.
характеристика рассеяния в единицах
признака Х
12

13. 2. Основные числовые характеристики выборки.

Существуют точечные и интервальные оценки параметров.
Определение 5.
Точечной оценкой φ* параметра φ
называют число, которое находят по
функции результатов наблюдения
φ* = φ*(x1, x2, . . ., xn), дает приближенное
значение теоретического параметра φ.

14. Требования к числовым оценкам ряда.

Она должна быть:
Несмещённой – если её математической ожидание
равно оцениваемому параметру при любом объёме
выборки.
Эффективной.
Эффективность
характеристика
точности – отношение дисперсии наилучшей
оценки и данной несмещённой оценки. Наилучшая
оценка – оценка с наименьшей дисперсией.
Состоятельной, если сходится по вероятности к
параметру φ, т.е. lim P(|φ* - φ|< ) = 1 при n
. Это равенство означает, что при достаточно
больших n, φ* отличается от φ на величину
меньшую, чем произвольное число .

15. Основные числовые характеристики выборки

1. Средняя выборочная (среднее взвешенное значение
признака в выборке):
к
i 1 хi ni
1
xв
( х1 n1 х2 n2 ... хk nk ).
n
n
(1)
15

16. Основные числовые характеристики выборки

1. Дисперсия выборочная. Характеризует разброс (рассеяние)
xв
значений вариант xi от выборочного среднего значения
измеряется в квадратных единицах признака Х:
1 k
1
2
2
2
2
Dв ( хi xв ) ni ( х1 xв ) n1 ( х2 xв ) n2 ... ( хк xв ) nk .
n i 1
n
( 2)
16
и

17. Основные числовые характеристики выборки

На практике используют ещё одну формулу для
расчёта дисперсии:
2
Dв xв
2
( xв ) ,
(3)
где
k
1
xв xi ni ;
n i 1
k
1
2
x xi ni .
n i 1
2
в
17

18. Основные числовые характеристики выборки

1. Среднее квадратичное отклонение выборки –
характеристика рассеяния значений признака в выборке
от среднего выборочного в единицах признака Х:
в Dв
.
(4)
18

19. Оценки имеют следующий вид (если n<30)

Оценки имеют следующий вид
(если n<30)
x xв ;
n
2
D
Dв Sв ;
n 1
n
Sв
Dв ,
n 1
(5)
(6)
2
где Sв - исправленная выборочная
дисперсия.
19

20.

Исправленная выборочная дисперсия:
( 7 )- ( 9 )
20

21. Основные числовые характеристики выборки

Определение 6.
Доверительным интервалом на основе точечной оценки φ*
наз
φ
с заданной надежностью P,
P(| (φ * - φ | < ) =p
ы
в
а
е
т
с
я
и
н
т
е
р
в
а
л
,
к
о
т
о
р
ы
й
п
о
к
р
ы
в
а
е
т
п
а
р
а
м
е
т
р
21

22. Доверительный интервал для нормально распределённой случайной величины

при n<30:
M (X ) X
t n, p S
n
( 10 )
,
где tn-1,p-коэффициент Стьюдента (таблица),
p- доверительная вероятность, равная 0,95.
при n>30:
M ( X ) X 1,96
n
;
( 11 )
22

23. 3. Нормальное распределение. Функция Гаусса. Гистограмма

Определение 7.
Гистограмма – графическое представление
частотного распределения количественной
случайной величины, сгруппированной в классы
равной ширины площадями прямоугольников.
Высоты каждого прямоугольника пропорциональны
частотам классов, а ширина интервала, одинаковая для
всех.
23

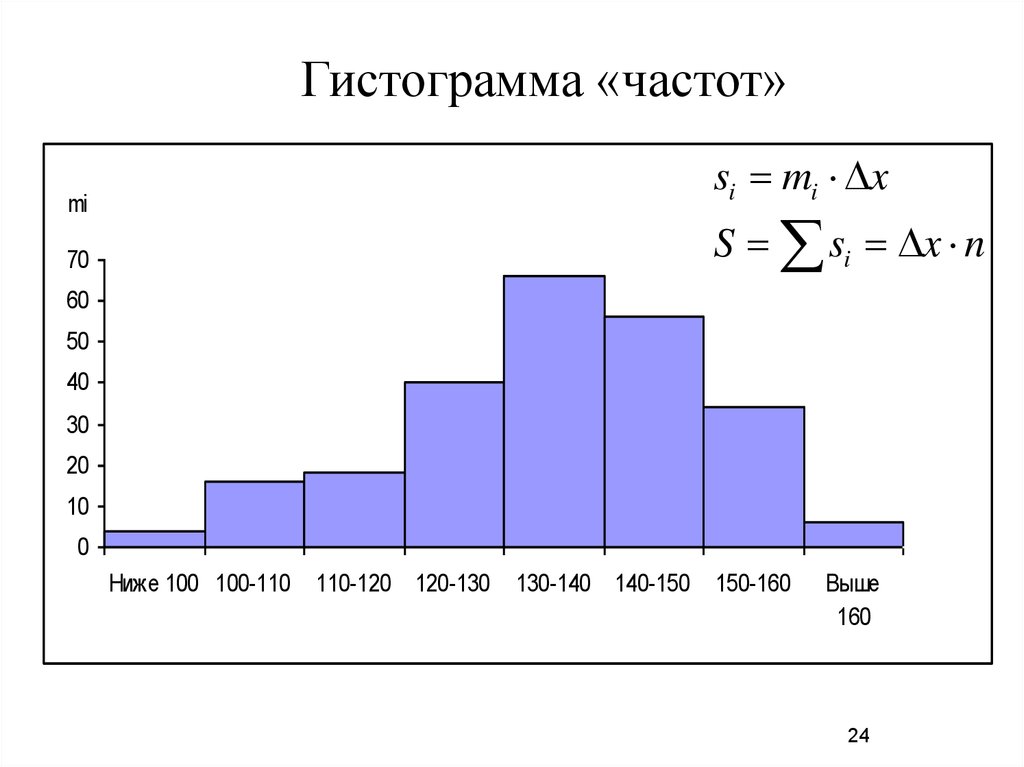
24.

Гистограмма «частот»
si mi x
mi
S si x n
70
60
50
40
30
20
10
0
Ниже 100 100-110
110-120 120-130
130-140 140-150
150-160
Выше
160
24

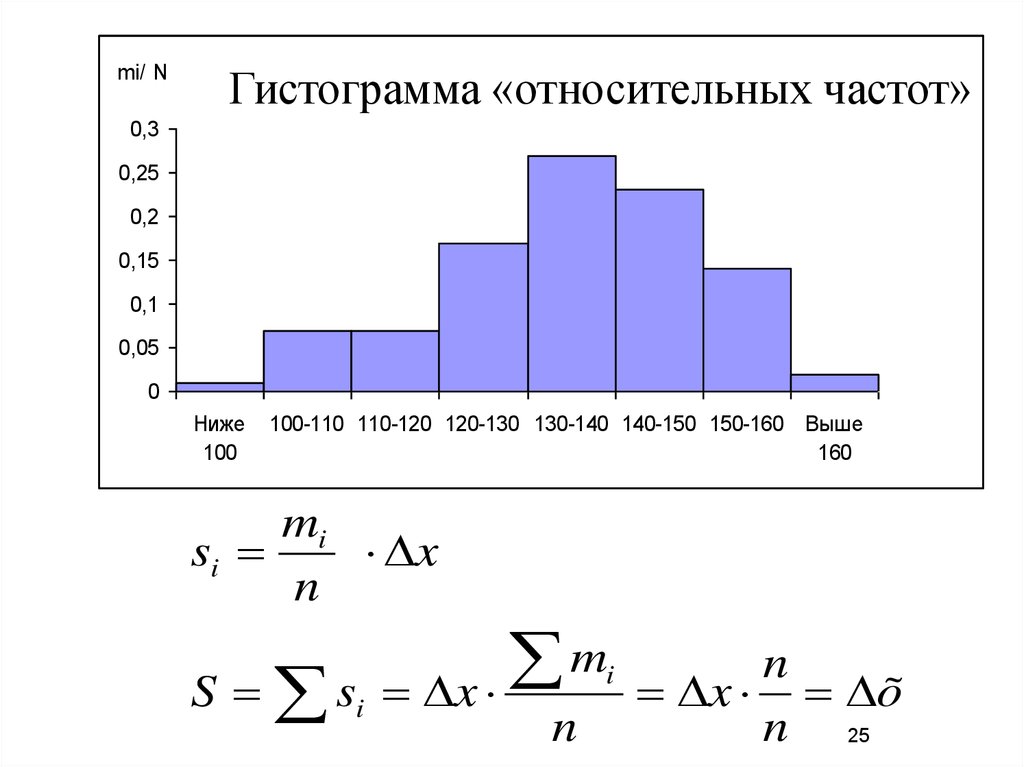
25.

mi/ N
Гистограмма «относительных частот»
0,3
0,25
0,2
0,15
0,1
0,05
0
Ниже
100
100-110 110-120 120-130 130-140 140-150 150-160 Выше
160
mi
si
x
n
m
S s x
n
i
i
n
x õ
n 25

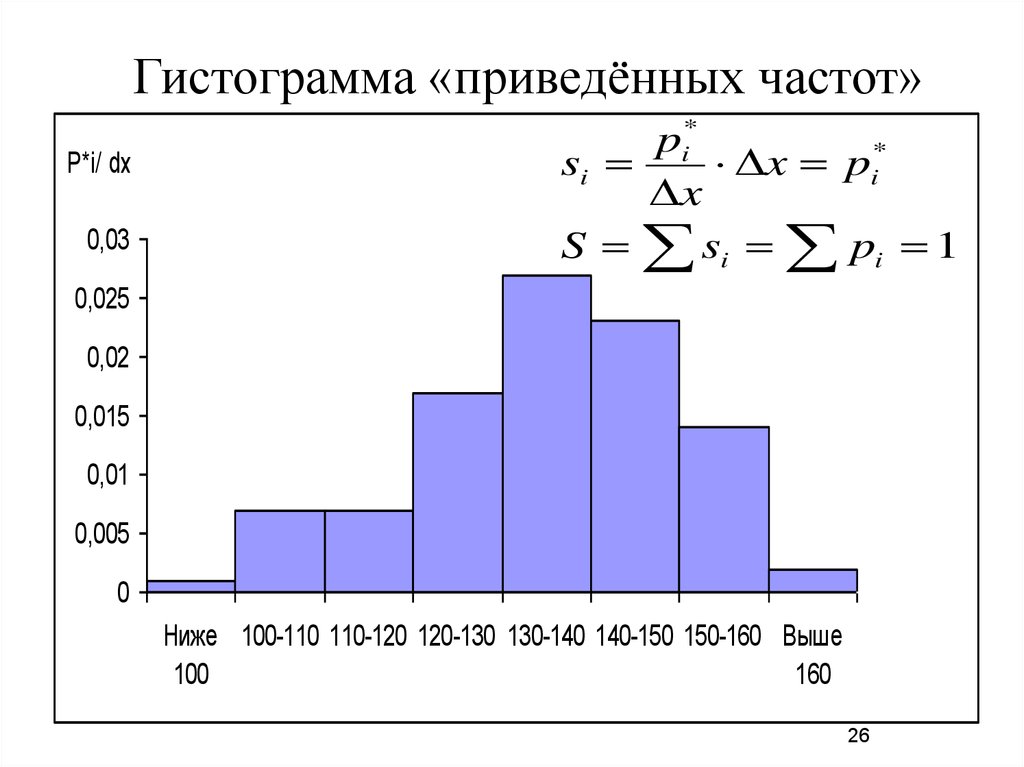
26.

Гистограмма «приведённых частот»
P*i/ dx
0,03
pi*
si
x pi*
x
S si pi 1
0,025
0,02
0,015
0,01
0,005
0
Ниже 100-110 110-120 120-130 130-140 140-150 150-160 Выше
100
160
26

27.

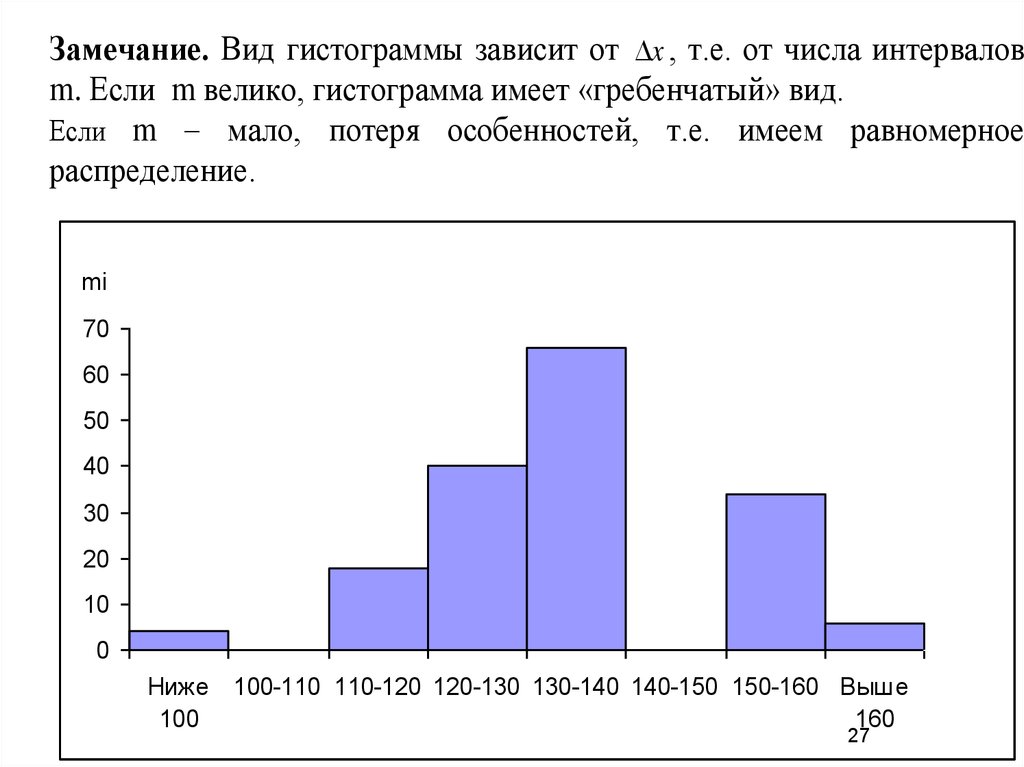
Замечание. Вид гистограммы зависит от x , т.е. от числа интервалов
m. Если m велико, гистограмма имеет «гребенчатый» вид.
Если m – мало, потеря особенностей, т.е. имеем равномерное
распределение.
mi
70
60
50
40
30
20
10
0
Ниже 100-110 110-120 120-130 130-140 140-150 150-160 Выше
100
160
27

28.

Согласно центральной предельной
теореме закон распределения суммы
большого числа независимых СВ, влияние
каждого из которых на всю сумму
ничтожно мало, близок к нормальному.
А.М.Ляпунов (1857 – 1918)
28

29. Нормальное распределение (распределение Гаусса).

f ( x)
1
2
e
( x x )2
2 2
функция Гаусса.
Это симметричная, быстро затухающая функция.
Имеет куполообразную форму с вершиной при x x ,
где x – определяет точку максимума
и ось симметрии, - расстояние от
этой оси до точки перегиба (M(X) = x , D(X) = ).
29

30.

функция Гаусса.
f ( x)
1
2
e
( x x )
2
2
30
2

31. Свойства нормального распределения:

а) Наиболее
вероятны значения x, близкие к
ожидаемому среднему значению
б) Отклонения от среднего значения
стороны равновероятны.
в обе
в) Большие отклонения x от среднего
значения маловероятны.
31

32. Свойства нормального распределения

г) При уменьшении увеличивается
вероятность значений, близких к ,
рассеяние уменьшается, кривая сжимается.
д) При увеличении график кривой
Гаусса становится более расплывчатым,
что говорит об увеличении рассеяния.
32