Химическая кинетика

1. ХИМИЧЕСКАЯ КИНЕТИКА

Химическая кинетика занимается изучением
механизмов и скоростей химических реакций. В
этом разделе физической химии изучается
влияние различных факторов – концентрации
реагирующих веществ, температуры, давления,
катализаторов и ингибиторов, состояния
поверхности (для гетерогенных процессов),
условий тепло- и масcообмена – на скорость
химических реакций

2. Контрольная работа № 3. Основы формальной кинетики Задание 1. Определение порядка и константы скорости реакции  

Контрольная работа № 3. Основы формальной
кинетики
Задание 1. Определение порядка и константы
скорости реакции
В реакторе при постоянном объеме V = 1 м3 и
температуре Т протекает газофазная реакция А. В
таблице 1 для этой реакции приведены результаты
измерений общего давления реакционной смеси Р в
зависимости от времени её протекания t. На основании
данных таблицы 1 исследуйте кинетику реакции A и
определите кинетические параметры: порядок реакции,
константу скорости, период полупревращения.

3. Порядок реакции - экспериментально определяемая величина, которую находят по результатам наблюдений за изменением концентраций

реагирующих веществ или
скорости во времени, то есть C = f(t) или = f(t)
Пример решения
2 N2O5 = 2 N2O4 + O2
В первую очередь нужно найти количество
вещества. Для этого используем химическую
переменную ξ

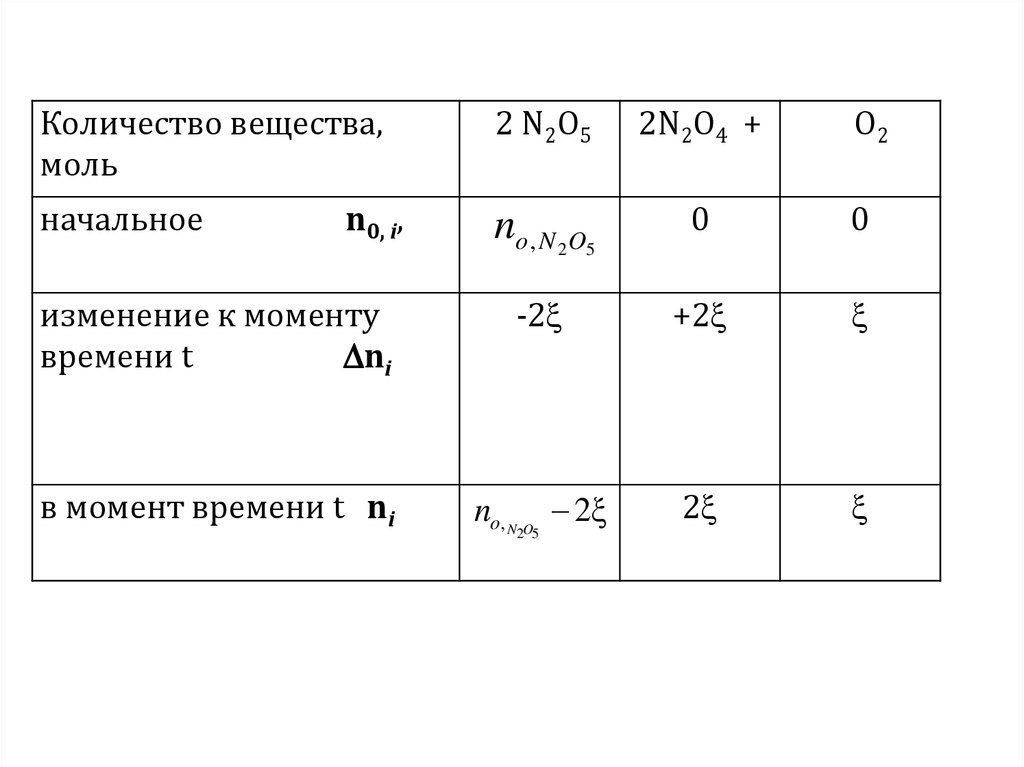
4.

Количество вещества,
моль
2 N2O5
2N2O4 +
начальное
no , N 2O5
0
0
изменение к моменту
времени t
ni
-2
+2
в момент времени t ni
no, N O 2ξ
2
n0, i,
2 5
O2

5.

Начальное количество исходного реагента N2O5
рассчитывается на основании величины общего
давления Pо в момент времени t = 0.
no , N 2 O5
Po V
RT
Тогда в любой промежуток времени t (кроме
начального) суммарное количество вещества газов
будет равно
n
i
i
nN 2O5 nN 2O4 nO2 no, N 2O5 2ξ 2ξ ξ no, N 2O5
PoV
ξ
ξ
RT

6. А также

Pt V
i ni nN2O5 nN2O4 nO2 RT
PV
(из уравнения Клапейрона-Клаузиуса n
)
RT
Pt – общее давление в реакторе в момент
времени t ≠ 0. Тогда получим
Po V
Pt V
ξ
RT
RT
nN 2 O5 no , N 2 O5
Pt V Po V
V
ξ
( Pt Po )
RT
RT
RT
Po V
V
V
3Po 2 Pt
2ξ
2
( Pt Po )
RT
RT
RT

7. Отсюда рассчитывается концентрации исходного вещества в различные промежутки времени

CN O
2
5
nN O
2
V
5
V
1
3Po 2Pt 3Po 2Pt
V RT
RT
Результаты вычислений концентрации
оксида азота(V) в каждый момент времени
поместим в таблицу

8. Вот она

Время t, с
0
150
Общее давление 73800
при Т = 317К
76750
P, Па
C N 2 O5 , моль/м3
28,0
25,8
325
700
1400
1800
Pt =
79900 85720 93780 97150
23,4
19,0
12,8
10,3

9. Далее переходим к определению порядка реакции графическим путем

Для этого продолжим предыдущую
таблицу, рассчитав для N2O5 в каждый
момент времени ещё следующее:
lnС, 1/С, 1/С2

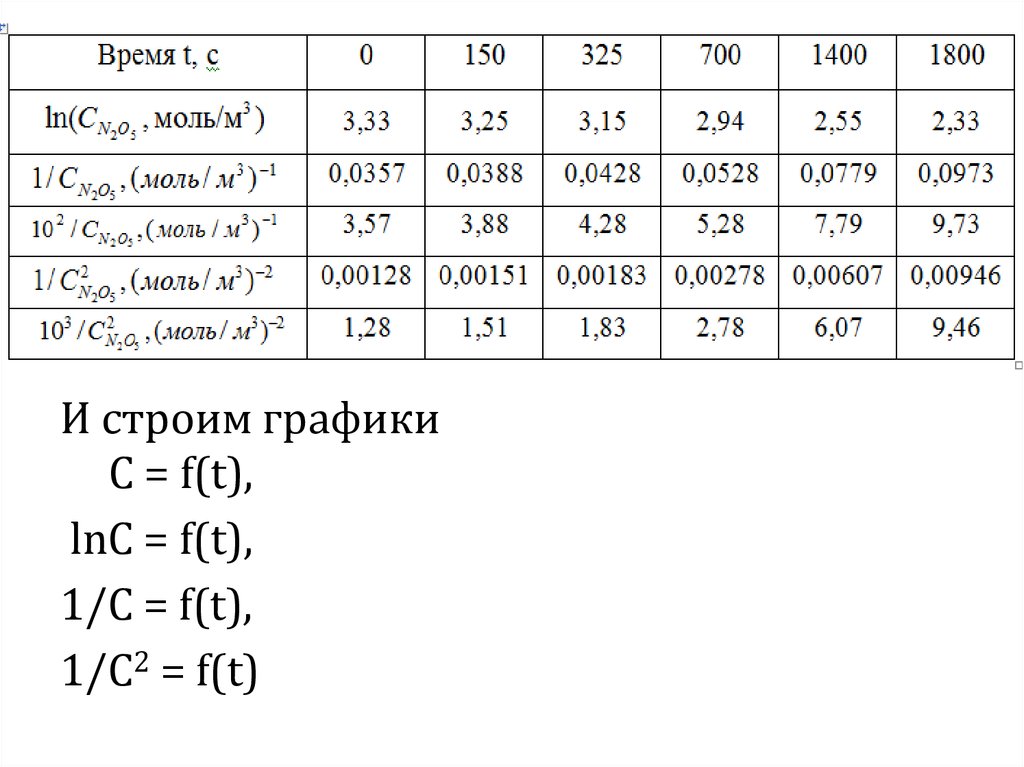
10.

И строим графики
С = f(t),
lnС = f(t),
1/С = f(t),
1/С2 = f(t)

11.

12.

13.

14.

С целью проверки правильности определения
порядка реакции воспользуемся методом
подстановки и для определения порядка реакции
данные для зависимости С = f(T) из таблицы
подставим поочерёдно в уравнения для скорости
процесса и рассчитаем константы скорости полагая,
соответственно, что реакция имеет нулевой,
первый, второй или третий порядок.

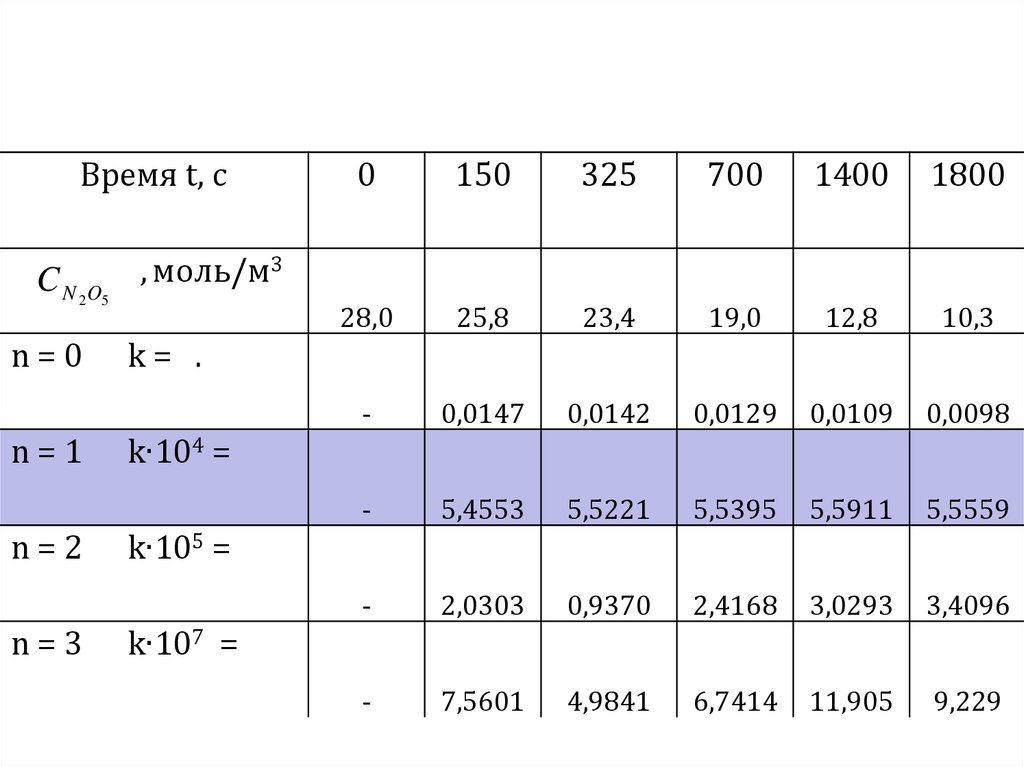
15.

Время t, с
C N 2 O5
n=0
n=1
n=2
n=3
0
150
325
700
1400
1800
28,0
25,8
23,4
19,0
12,8
10,3
-
0,0147
0,0142
0,0129
0,0109
0,0098
-
5,4553
5,5221
5,5395
5,5911
5,5559
-
2,0303
0,9370
2,4168
3,0293
3,4096
-
7,5601
4,9841
6,7414
11,905
9,229
, моль/м3
k= .
k∙104 =
k∙105 =
k∙107 =

16.

Из таблицы хорошо видно, что только
расчет константы по уравнению для
первого порядка
1
ki ln( C0 / C )
ti
даёт значение константы скорости,
которое остаётся во времени
практически неизменным
k1 ≈ k2 ≈ k3 ≈ k4 ≈ k5
Этим мы подтверждаем результаты,
полученные графическим методом

17.

.
Тогда константа скорости химической реакции
первого порядка будет равна
1 C0, N 2O5
k ln
t C N 2O5
,
а период полупревращения:
t1/ 2
1
ln 2
ln 2
1253c
4
k
5,53 10

18. Если известно, что к моменту времени t15% прореагировало 15 % исходного количество N2O5, то значит текущее значение

концентрации
через t15% с будет равно
C N 2O5 C0, N 2O5
C0, N 2O5
100%
15% 0,85 C0, N 2O5
подставляя это в интегральную форму
кинетического уравнения реакции (дано в
разделах 4.1-4.4)получим
ln( 0,85 C0, N O ) ln C0, N 2O5 k t15%
2 5
t15%
1 C0, N 2O5
ln
k 0,85 C0, N O
2 5
1 1
ln
k 0,85
1
1
ln
293,9 c
4 1
0,85
5,53 10 c

19.

• Теперь, чтобы найти концентрацию N2O5
в момент времени t1 = 12 мин от начала
реакции, в интегральное кинетическое
уравнение подставим значения
начальной концентрации, константы
скорости и времени и тогда получим
ln CN2O5 ln C0, N2O5 k t ln 28 5,53 10 4 c 1 12 мин 60 с / мин 2,934
CN2O5 exp( 2,934) 18,8 моль/м
3

20. Задание 2. Определение параметров температурной зависимости скорости химической реакции

В таблице приведены значения констант скоростей k1 и k2 для реакции A
при температурах T1 и T2, соответственно. Используя величины k1 и k2, а
также значение константы скорости k, полученное при выполнении
предыдущего задания для температуры T, постройте график в
координатах lg k = f(1/T) и определите:
а) коэффициенты A и B в интегральной форме уравнения Аррениуса вида lgk = A – B/T и
составьте это уравнение с численными значениями A и B для химической реакции А;
б) графически и аналитически энергию активации (Eакт, кДж/моль) химической реакции
А;
в) величину предъэкспоненциального множителя в экспоненциальной форме уравнения
температурной зависимости скорости (уравнение Аррениуса) и составьте это
уравнение с численными значениями параметров для химической реакции А;
г) температурный коэффициент скорости химической реакции А для интервала
температур от T1 до T2;
д) константу скорости k3 реакции В при температуре Т3.
е) как изменится скорость химической реакции А, если температуру Т1 изменить на ∆Т.

21. Исходные данные

Температура
T, К
Т1
Т
Т2
Т3
325
317
310
330
104 / T, К-1
30,8
31,5
32,3
k1
kсред
k2
1,15·10-3
5,53·10-4
2,86·10-4
-6,768
-7,500
-8,160
k, с-1
ln (k, с-1)
Из предыдущей задачи
k3

22. Зависимость скорости химической реакции от температуры в дифференциальной форме имеет вид

E акт
d ln k
2
dT
RT
где R – универсальная газовая постоянная, а Eакт
– энергия активации химической реакции.
Интегрируя это выражение, называемое
уравнением Аррениуса, при условии, что Eакт не
является f(T), приходят к его интегральной
форме, которую записывают в виде зависимости
B
ln k A
T

23. график является прямой линией в координатах ln k = f(1/T)

где A – константа
интегрирования,
B = Eакт /R
График – прямая вида y=a±bx, т.е
у= ln k
x=1/T
Можно вычислить энергию активации химической
реакции по представленным данным, т.к. известны
константы скоростей при двух температурах.

24. Но должно выполнятся условие что Eакт не зависит от температуры в рассматриваемом интервале

Чтобы убедиться в выполнении этого условия,
необходимо построить график в координатах
ln k = f(1/T). Для построения графика
воспользуемся данными таблицы
аналитическая формула для расчета
энергии активации имеет вид
E
эксп .
акт .
T1 T2
k1
R
ln
T1 T2
k2

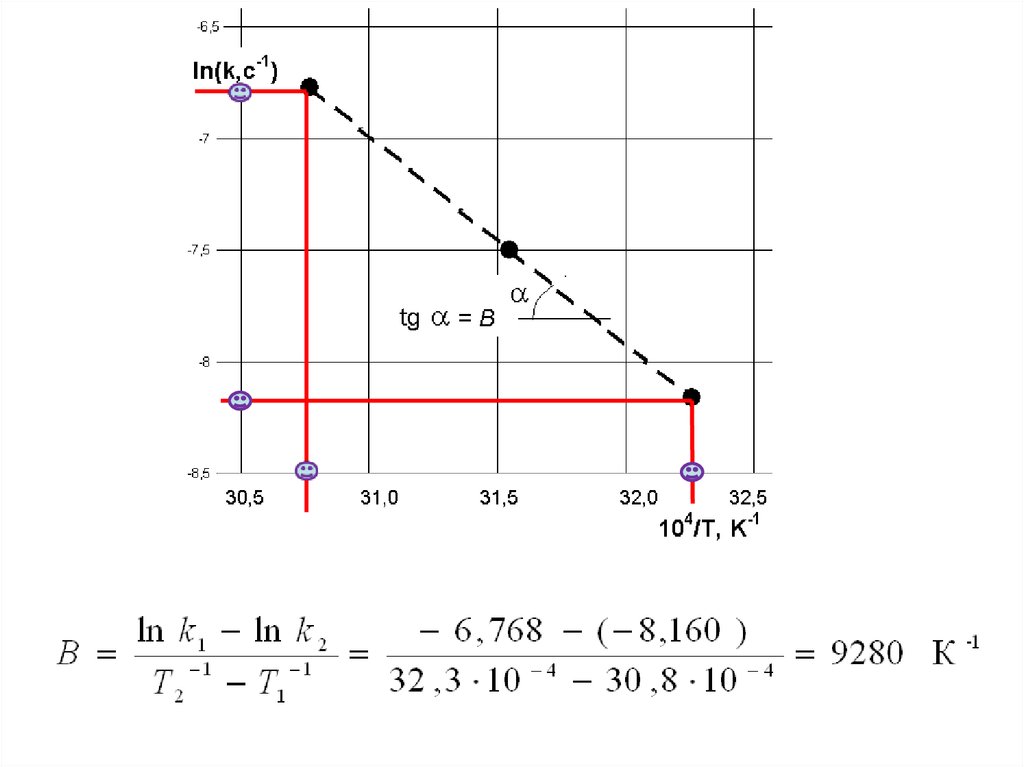
25.

Из рисунка видно, что все точки лежат на прямой линии,
значит, условие что Eакт не зависит от температуры
выполняется и можно продолжать расчеты

26.

Графически коэффициент В
можно представить как
тангенс угла наклона прямой
к оси абсцисс.
Он рассчитывается как
отношение длины
противолежащего катета к
длине прилежащего.
При этом длины катетов выражаются
в соответствии с величинами,
отложенными по осям координат

27.

28.

Eакт = B R = 9280 К-1 8.31 = 77116,8 Дж/моль 77,1 кДж/моль
Определим предэкспоненциальный множитель k0 в
уравнении Аррениуса:
Eакт
77700
3
9 -1
k o kT exp
1,15 10 exp
3,59 10 c
8.31 325
RT
и составим уравнение Аррениуса для реакции
в экспоненциальной форме:
E
77700
9350
9
k k o exp акт 3,59 109 exp
3
,
59
10
exp
RT
8
.
31
T
T
9350
k 3,59 109 exp
T

29. Для определения температурного коэффициента скорости реакции (γ) в интервале температур от 310 до 325 К воспользуемся правилом

ВантГоффа
При повышении температуры на каждые 10
градусов скорость химической реакции
увеличивается в среднем в γ раз.
Величина температурного коэффициента скорости
химической реакции γ, как правило, изменяется в
пределах от 2 до 4
kT
1
kT
2
γ
T1 T2
10
k325
( 325 310) / 10 1,15 10 3
γ
4
2
,
86
10
k310
γ1,5 = 4,02

30.

Логарифмируя левую и правую части,
получим:
1,5 ln γ = ln 4,02
ln γ = (ln 4,02)/1,5
γ = exp[(ln 4,02)/1,5) = 2,53
Зная температурный коэффициент скорости
реакции определим, во сколько раз
изменится скорость реакции, если
температуру Т изменить на 30 К:
Скорость изменится в γ 30/10 = 2.533 = 16,2
раза