Similar presentations:
Geometric Transformations
1. Geometric Transformations
Zeid, I., Mastering CAD/CAM, Chapter 12Spring, 2018 AUA
2. Intro & General Information
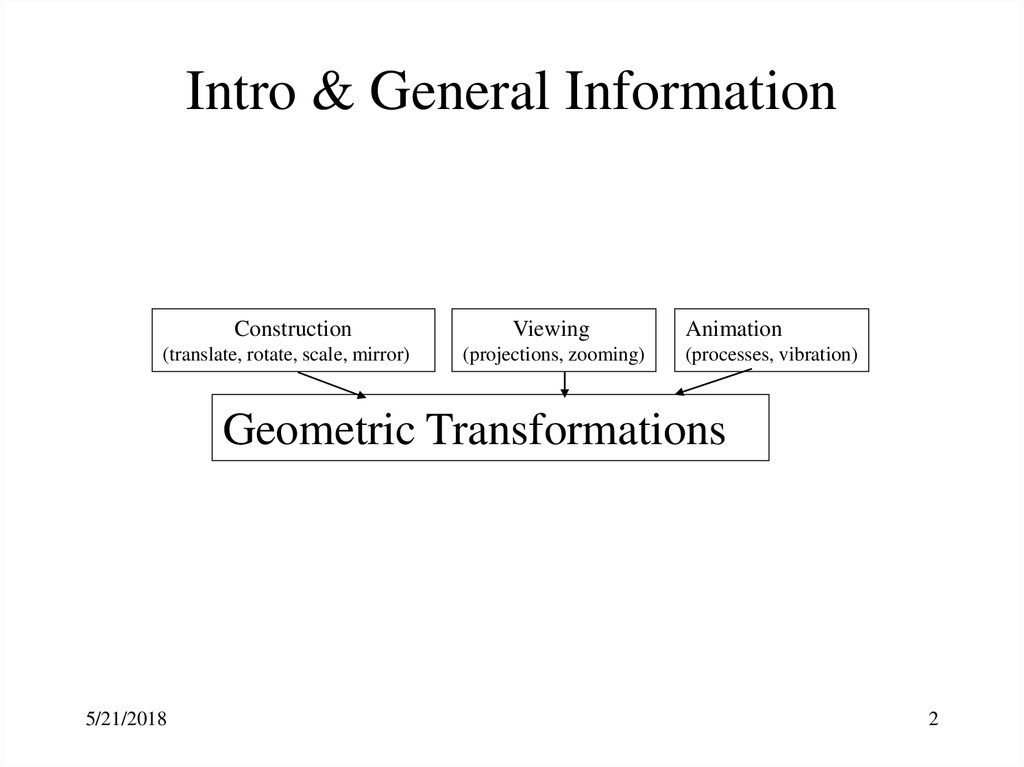
Intro & General InformationConstruction
(translate, rotate, scale, mirror)
Viewing
(projections, zooming)
Animation
(processes, vibration)
Geometric Transformations
5/21/2018
2
3. General Information
Transformation of a point is basic in GT. It can be formulated as follows:Given a point P that belongs to a geometric model find the corresponding
point P* in the new position such that
P* = f(P, transformation parameters)
• The transformation parameters should provide ONE-TO-ONEMAPPING.
• Multiple transformations can be combined to yield a single
transformation which should have the same effect as the sequential
application of original ones. CONCATENATION /kənˌkatnˈāSH(ə)n/
Equation of P* for graphics hardware should be in matrix notation:
P* = [T]P,
where [T] is the transformation matrix.
5/21/2018
3
4. Translation
Translation is a rigid-body transformation (Euclidean) wheneach entity of the model remains parallel, or each point
moves an equal distance in a given direction:
P* = P + d (for both 2D and 3D). In a scalar form (for 3D):
x * = x + xd
y
y* = y + yd
B (10,8)
z* = z + zd
C (11,7)
B*
A (8,5)
C*
A*
x
O
Question: Find the coordinates of vertices A*, B*,
and C* of the translated triangle.
The distance vector of translation: D = [-7 -4]T.
Verify that the lengths of the edges are unchanged.
5/21/2018
4
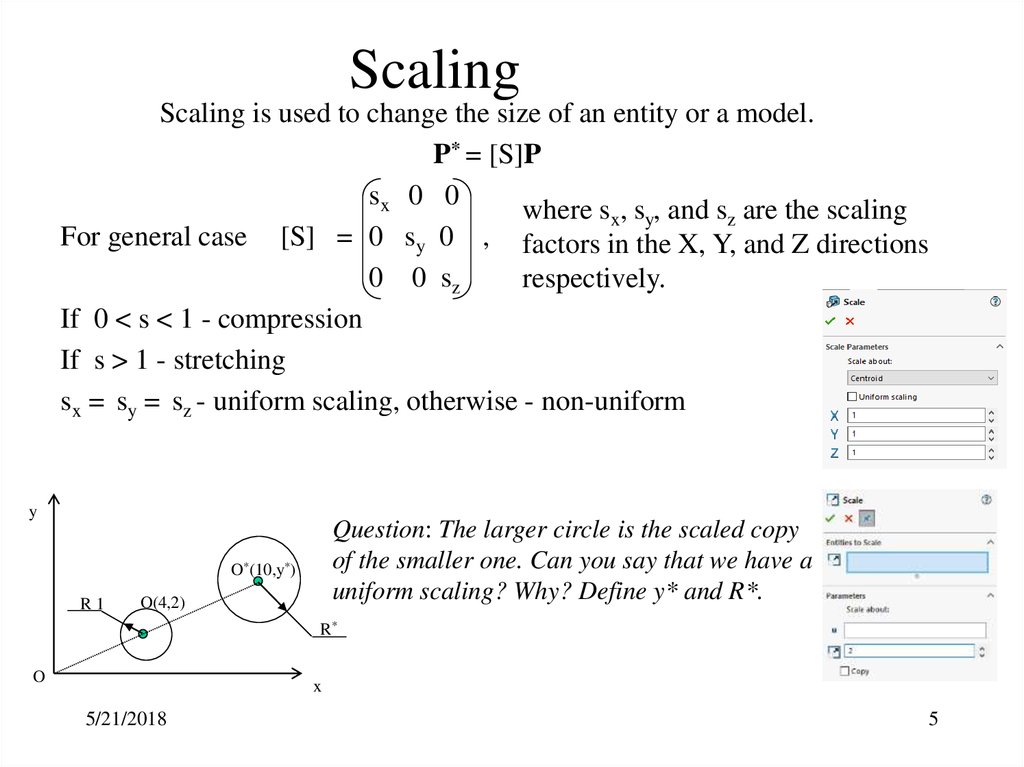
5. Scaling
Scaling is used to change the size of an entity or a model.P* = [S]P
sx 0 0
where sx, sy, and sz are the scaling
For general case [S] = 0 sy 0 , factors in the X, Y, and Z directions
0 0 sz
respectively.
If 0 < s < 1 - compression
If s > 1 - stretching
sx = sy = sz - uniform scaling, otherwise - non-uniform
y
Question: The larger circle is the scaled copy
of the smaller one. Can you say that we have a
uniform scaling? Why? Define y* and R*.
O*(10,y*)
R1
O(4,2)
R*
O
x
5/21/2018
5
6. Mirror
Plane* => Negate the corresponding coordinateMirror through Line* => Reflect through 2 planes intersecting at the axis
Point* => Reflect through 3 planes intersecting at the point
* plane - principal plane, line - X, Y, or Z axes, point - CS origin
P* = [M]P,
1 0 0
m11 0
0
where
[M] =
0 1 0
0 m
0 =
22
0
0
m33
0
0
1
Question: Define the signs (in the matrix)
for the reflections (mirroring) through:
a) x = 0, y = 0, z = 0 planes
b) X, Y, and Z axes
c) the CS origin
5/21/2018
6
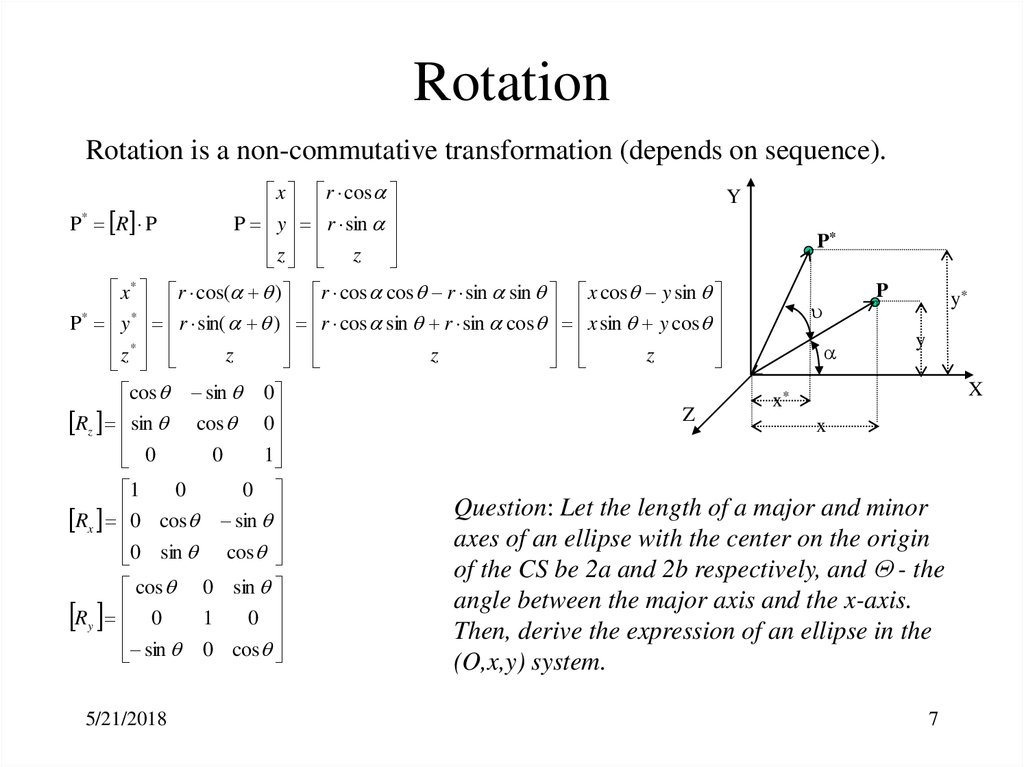
7. Rotation
Rotation is a non-commutative transformation (depends on sequence).P* R P
x r cos
P y r sin
z z
Y
P*
x* r cos( ) r cos cos r sin sin x cos y sin
P* y * r sin( ) r cos sin r sin cos x sin y cos
z *
z
z
z
cos sin 0
Rz sin cos 0
0
0
1
0
0
1
Rx 0 cos sin
0 sin cos
cos 0 sin
R y 0
1
0
sin 0 cos
5/21/2018
Z
P
y*
y
X
x*
x
Question: Let the length of a major and minor
axes of an ellipse with the center on the origin
of the CS be 2a and 2b respectively, and - the
angle between the major axis and the x-axis.
Then, derive the expression of an ellipse in the
(O,x,y) system.
7
8. Homogeneous Transformation - 1
When we scale then rotate, the transformed image is given by:P* = ([R][S])P
where [S], [R], [R] [S] are 3x3 transformation matrices. This is not the case
for a translation (P* = P + d). The goal is to find a [D] such that
P + d = [D]P
in order to perform valid matrix multiplication.
This is found by using a homogeneous coordinates.
Homogeneous Transformation maps n-dimensional space into (n+1)- dim.
3D representation of the point vector - P = [x, y, z]T
Homogeneous rep. of the same vector - P = [xw, yw, zw, w]T where w = 1
5/21/2018
8
9. Homogeneous Transformation - 2
The transformation matrices in new (homogeneous) representation:1
0
D
0
0
1
0
M
0
0
5/21/2018
0
0
1
0
0
1
0
0
xd
yd
zd
1
0
0
1
0
0
1
0
0
0
0
0
1
sx
0
S
0
0
r11
r
R 21
r31
0
0
0
sy
0
0
sz
0
0
r12
r13
r22
r23
r32
r33
0
0
0
0
0
1
0
0
0
1
9
10. Composition of Transformations
Now we are able to include all the transformations in a single matrix. Incase of composition of transformations: P* = [Tn][Tn-1]...[T2][T1]P,
where [Ti] are different transformation matrices.
Sequence is important!
Practice: Mirror point A through the given line and find x and y.
y
450
A* (x,y)
(1,6)
O
5/21/2018
A (8,5)
x
10
11. Another example
Scale line AB about point M by factor of
2 and then mirror new line A’B’ about the
origin.
A(-1, 2)
B(3,-2)
M(-2,-2)
5/21/2018
11








 mathematics
mathematics








