Решение задач

1.

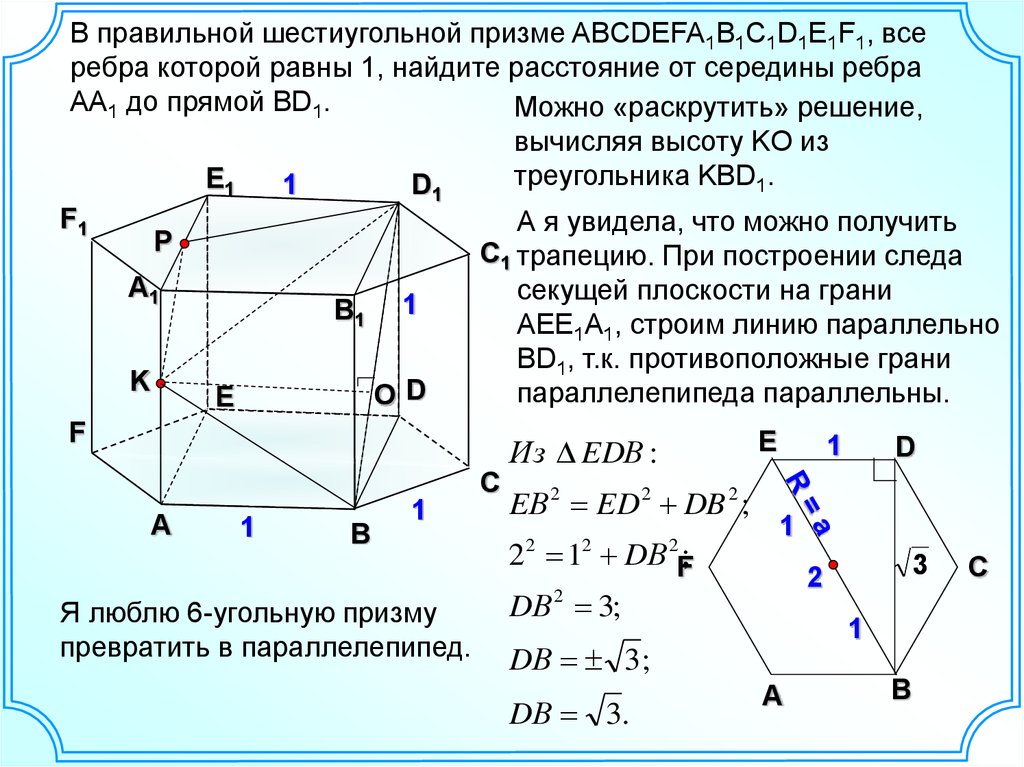
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, все
ребра которой равны 1, найдите расстояние от середины ребра
AA1 до прямой BD1.
Можно «раскрутить» решение,
вычисляя высоту KO из
треугольника KBD1.
E1
1
D1
F1
А я увидела, что можно получить
P
C1 трапецию. При построении следа
А1
секущей плоскости на грани
1
B1
AEE1А1, строим линию параллельно
BD1, т.к. противоположные грани
K
параллелепипеда параллельны.
OD
E
F
E
1
D
Из EDВ :
C
A
1
B
1
Я люблю 6-угольную призму
превратить в параллелепипед.
EВ 2 ED 2 DB 2 ;
2 1 DВ F;
2
2
2
1
DВ 2 3;
1
DВ 3;
DВ 3.
3
2
A
B
С

2.

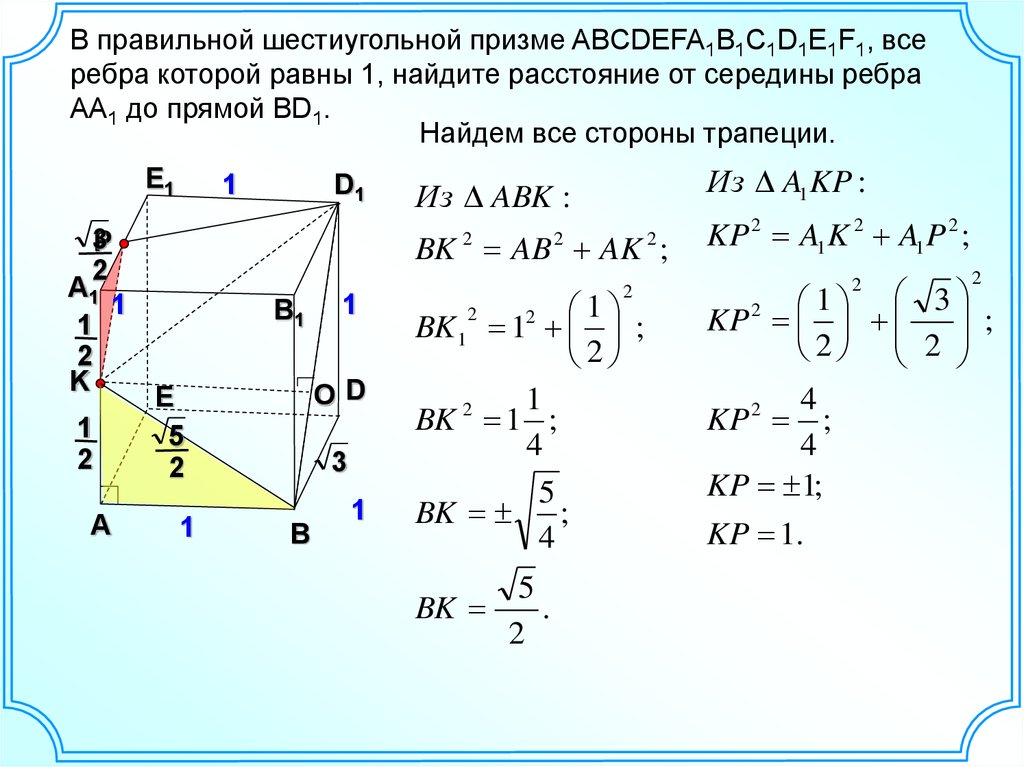
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, все
ребра которой равны 1, найдите расстояние от середины ребра
AA1 до прямой BD1.
Найдем все стороны трапеции.
E1
3
P
2
А1
1
1
2
K
1
2
A
1
D1
Из A1 KP :
Из ABK :
BK AB AK ;
2
B1
OD
E
5
2
1
1
3
B
1
2
2
2
1
BK 1 1 ;
2
1
BK 2 1 ;
4
5
BK ;
4
2
BK
2
5
.
2
KP 2 A1 K 2 A1 P 2 ;
2
1 3
2
KP
;
2 2
4
KP 2 ;
4
KP 1;
2
KP 1.

3.

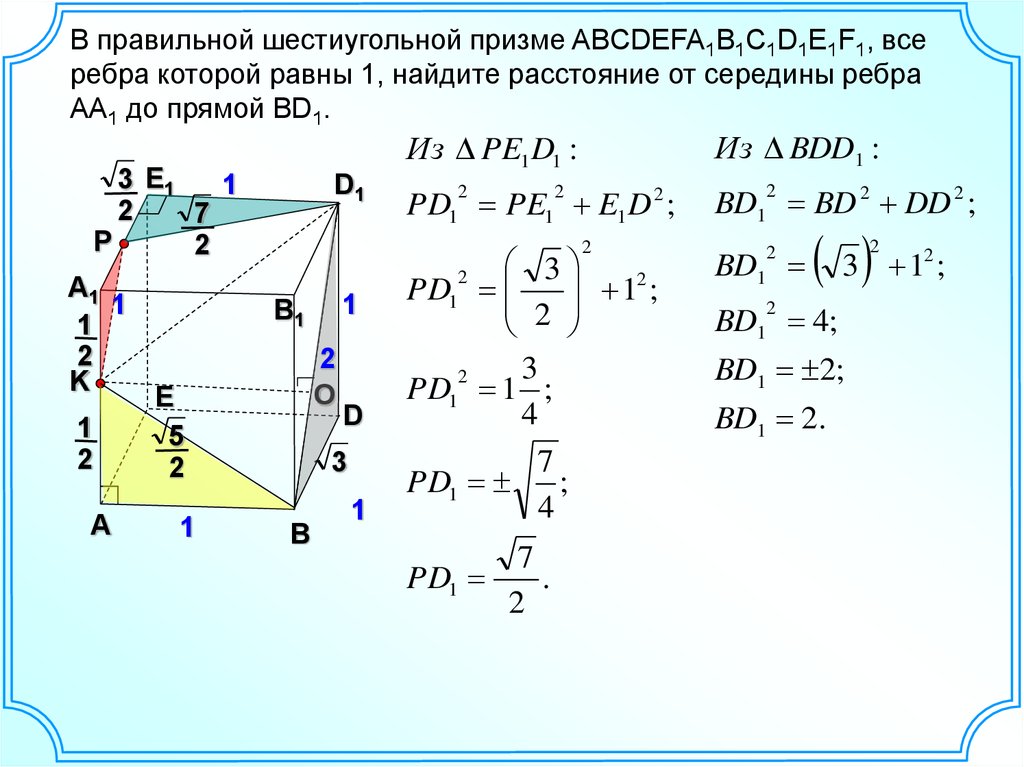
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, все
ребра которой равны 1, найдите расстояние от середины ребра
AA1 до прямой BD1.
3 E1
1
2
7
P
2
А1
1
1
2
K
1
2
A
D1
Из PE1 D1 :
Из BDD1 :
PD1 PE1 E1 D 2 ;
BD1 BD 2 DD 2 ;
2
2
3
12 ;
PD1
2
3
2
PD1 1 ;
4
7
PD1 ;
4
2
1
B1
2
O
E
5
2
1
2
D
3
B
1
7
PD1
.
2
2
BD1
2
3 1 ;
BD1 4;
2
BD1 2;
BD1 2.
2
2

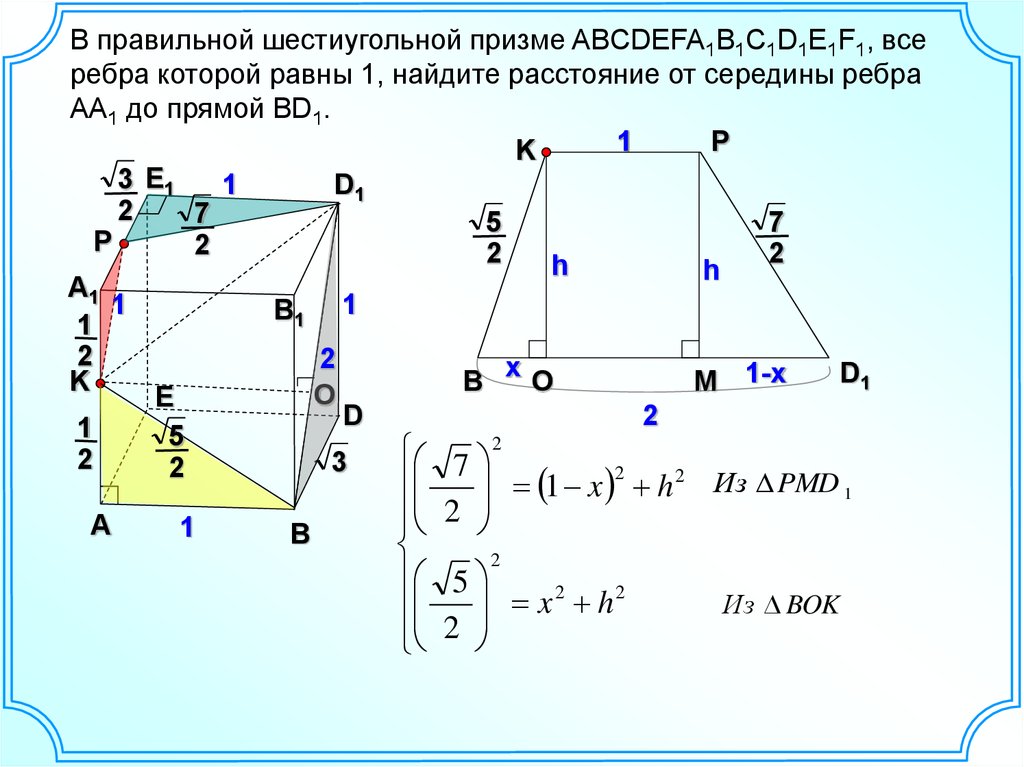
4.

В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, все
ребра которой равны 1, найдите расстояние от середины ребра
AA1 до прямой BD1.
1
P
K
3 E1
1
D1
2
7
5
7
P
2
2
2
h
h
А1
1
B1 1
1
2
2
xO
1-x
D1
K
B
M
O
E
D
2
1
5
2
2
3
7
2
1 x 2 h 2 Из PMD 1
2
A
1
B
2
5
x2 h2
2
Из BOK

5.

2
7
1 x 2 h 2
2
2
5
x2 h2
2
E1
D1
P
А1
K
O
E
A
1
B1
B
D
7
2
2
1
2
х
x
h
4
«–»
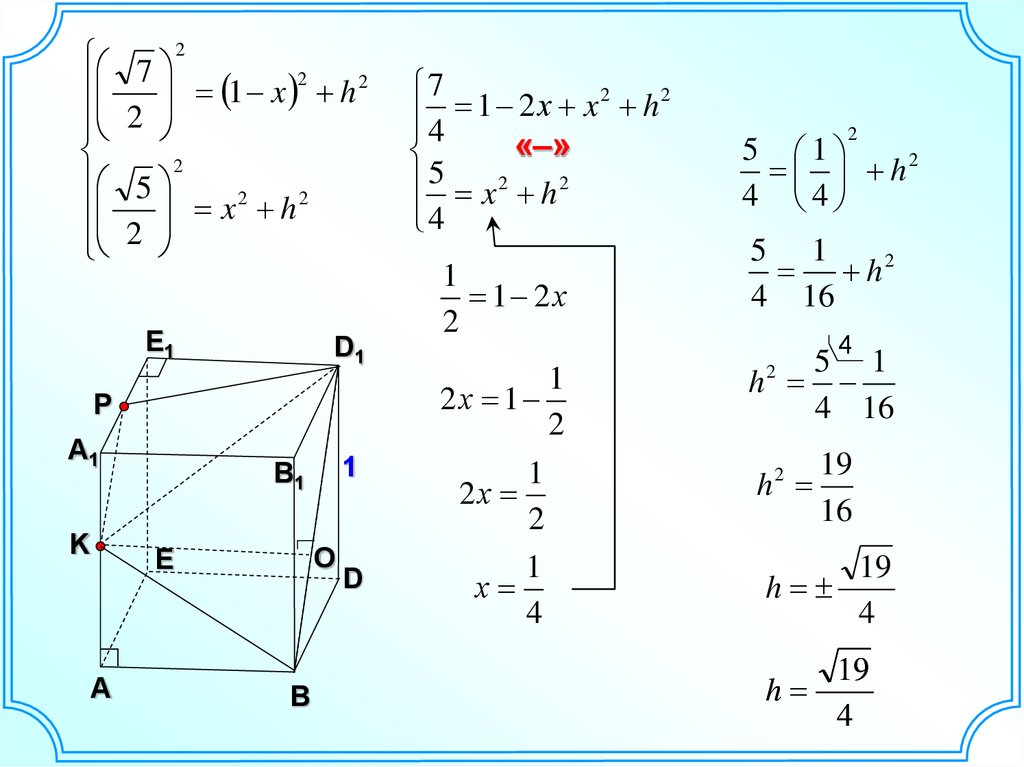
5 x2 h2
4
1
1 2х
2
1
2х 1
2
1
2х
2
1
х
4
2
5 1
h2
4 4
5 1
h2
4 16
4
5 1
2
h
4 16
19
h
16
2
h
h
19
4
19
4