Similar presentations:
Критичность ограниченных размножающих сред
1. Критичность ограниченных размножающих сред
кафедра«Теоретическая и
эксперимент а льная физика
ядерн ых ре акторов»
доцент
Савандер В. И .
2. Одногрупповое диффузионное приближение
Для выяснения чисто пространственных эффектов в
конечных размножающих средах введем ряд упрощающих
предположений:
• Рассматривается однородная размножающая среда,
занимающая некоторый объем V;
• Пренебрегаем энергетической зависимостью потока
нейтронов (одногрупповое приближение)
• Для учета углового распределения нейтронов рассмотрим
функцию полного потока и полного тока нейтронов (P1 –
приближение)
( r ) d ( r , ), I ( r ) ( r , )d
4
4
3. Одногрупповое диффузионное приближение
• В отсутствии в размножающей среде сильныхлокальных поглотителей и для областей активной
зоны, удаленных от границы реактора с пустотой
связь между этими величинами дается законом
Фика:
1
I - D где D
3 tr
, tr t - s
• Одногрупповое диффузионное приближение
n
divI ( r , t ) a Ф( r , t ) f f Ф( r , t ),
t
Ф( r , t ) V n ( r , t ).
4. Одногрупповое диффузионное приближение
Для стационарного случая( r, t ) ( r ),
D Ф( r ) a Ф( r ) f Ф( r ) 0.
Рассмотрим простейший случай так называемого «голого»
реактора, когда размножающая среда граничит с вакуумом.
В одногрупповом диффузионном приближении точное
граничное условие заменяется приближенным
( rs ) 1
i ( rs ) 0, i ( rs )
D
( rs ) 0.
4
2 n
5. Одногрупповое диффузионное приближение
• Разлагая Ф(r) вблизи границы с вакуумом в ряд долинейного члена, получим:
Ф
x
Ф( rs x n ) Ф( rs )
( rs ) x Ф( rs )(1
).
n
2D
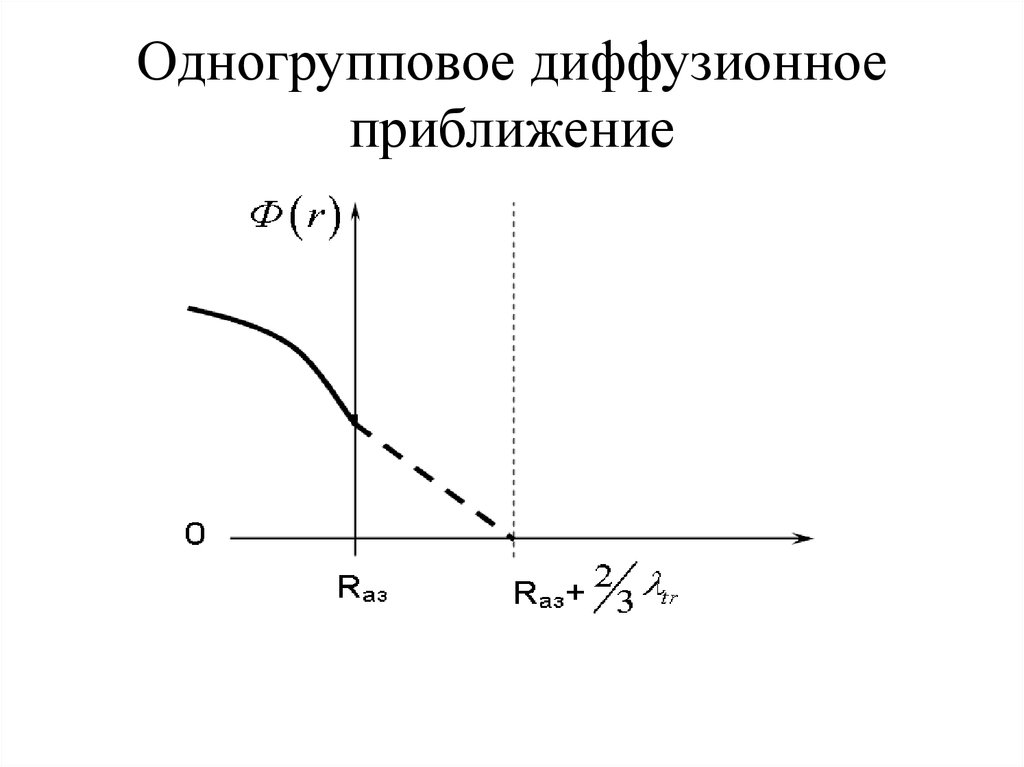
• Если теперь экстраполировать распределение
нейтронов за пределы среды в пустоту, то
экстраполированный поток нейтронов обратится в
2
нуль на расстоянии
x
3
tr
• от геометрической границы реактора. Эта величина
называется экстраполированной добавкой среды
6. Одногрупповое диффузионное приближение
7. Одногрупповое диффузионное приближение
• общая постановка задачи в одногрупповомдиффузионном приближении такова: требуется
найти ограниченное положительное решение
задачи:
D Ф( r ) a Ф( r ) f Ф( r ) 0,
Ф( rextr ) 0.
• Введем следующие обозначения:
f
K 1
D
2
; K
, L
2
a
a
L
2
8. Одногрупповое диффузионное приближение
K 1 материальный параметр среды
2
L
2
D
L
a
- длина диффузии нейтронов в
размножающей среде
Ф Ф 0,
2
Ф ( rextr ) 0.
• Это задача на определение собственных чисел и
собственных функций оператора Лапласа
9. Одногрупповое диффузионное приближение
• Наименьшему собственному значениюсоответствует знакопостоянная собственная
функция
(r )
0
0 ( r )
2
- 0 0 ( r ),
0 ( rextr ) 0.
• Стационарное решение будет только в том случае
2 02
• Величина (α0)2 - геометрический параметр
определяется геометрией объема среды.
10. Одногрупповое диффузионное приближение
• Функция пространственного распределения потоканейтронов
Ф( r ) C 0 ( r )
• условие критичности реактора и означает, что для
размножающей среды заданной геометрической формы
существуют такие размеры, при которых в этой среде
возможен стационарный процесс размножения нейтронов
(деления ядер). Соответствующие размеры такой среды
называются критическими размерами, а отвечающий этим
размерам объем мультиплицирующей среды –
критическим объемом. Масса делящегося вещества в
такой среде называется критической массой.
11. Сферический реактор
• В сферически симметричном случае1 d 2 d
лапласиан имеет вид:
r
r 2 dr
dr
• геометрический параметр определяется из
решения волнового уравнения:
1 d 2 d
2
r
0,
2
dr
r dr
( rextr ) 0.
12. Сферический реактор
• Общее решение этого уравнения( r ) C1
sin( r )
cos( r )
C2
.
r
r
• Условие ограниченности решения задачи
( r ) C
• Граничное условие
sin( r )
r
sin( R ) 0; n R ( n 1), n 0,1,...
n
( n 1), 0 .
R
R
• Условие критичности
K 1
2
L
R
2
13. Сферический реактор
• Критический радиус активной зоныR
, R
L.
( K 1)
• Константа C определяется из условия нормировки
R0
R0
на мощность
2
2
W E f f ( r ) 4 r dr 4 C E f f sin( 0 r ) r dr
0
0
• Пространственное распределение потока
нейтронов характеризуется спадом потока
нейтронов к границе реактора, поскольку через
границу реактора происходит утечка нейтронов в
вакуум
14. Сферический реактор
15. Цилиндрический реактор
Рассмотрим цилиндрическую активную зонурадиуса R и высоты H
Задача на определение геометрического параметра
1 2
r
2 2 0, ( r, z )
r r r z
H
( R , z ) 0 z , ( r , ) 0 r ,
0, z 0 z
2
r
16. Цилиндрический реактор
• Метод разделения переменных ( r, z ) Y ( r ) Z ( z )1 1 d dY
r
Y r dr dr
2
1d Z
2
Z dz 2
2 2r 2z
1 d dY
r
2r Y 0,
r dr dr
d 2Z
2
z Z 0,
2
dz
dY
(0) 0, Y ( R ) 0,
dr
dZ
H
(0) 0, Z 0
dz
2
17. Цилиндрический реактор
• Общее решение уравнений с учетомограниченности потока нейтронов
Y ( r ) C1 J 0 ( r r )
Z ( z ) D1 sin( z z ) D2 cos( z z )
• Из краевых условий
J 0 ( r R ) 0, r R n , (rn )
H
cos z
2
n
,
R
H
(n)
0,
(
n
1),
( n 1)
z
z
2 2
H
18. Цилиндрический реактор
• геометрический параметр для цилиндрическойактивной зоны и распределение плотности потока
нейтронов в реакторе:
0 , (0)
,
z
R
H
2
2
0
2
(0)
r
0
R H
( r, z ) C J 0 0 r cos z , 0 2.405
R
H
2
• Условие критичности
2
K 1
2.405
L2
R H
19. Цилиндрический реактор
Рассмотрим частный случай2r 2 , R 0
то критичность реактора достигается при
бесконечной высоте . Для тех цилиндров, радиус
которых меньше R, критичность не достигается ни
при каком значении высоты цилиндра.
2
2
,
Н
Eсли высоту цилиндра взять из условия z
то критичность такого реактора достигается только
при бесконечно большом радиусе цилиндра. Если
высота активной зоны меньше H, то реактор при
любом радиусе будет подкритичным. Это примеры
некритических объемов.
20. Цилиндрический реактор
• Из условия критичности для цилиндра следует,что при заданном материальном параметре
размножающей среды получается бесконечное
множество критических активных зон. Среди них
есть такой цилиндр, у которого минимальный
объем.
• Постановка задачи: найти минимум функции двух
переменных V R 2 H с учетом условия связи
между переменными 2 2
0
2
H R
21. Цилиндрический реактор
• используя ограничение, выразим одну изпеременных через другую
2
2
2
3
H
H
0
R2 2 0 2
,
V=
H 2
2 H 2 2
• Условие экстремальности критического объема
2
2 2
3
2 4
dV
2 3H ( H ) 2 H
0
0
2 2
2 2
dH
( H )
• находим радиус и высоту оптимального цилиндра:
3
2
H
, R 0 ,
3
(цил)
Vкр
3 3 2 02
,
3
(цил)
Vкр
(сфер)
Vкр
9 3 02
1.14
2
4
22. Сферический реактор
• Рассмотрим влияние плотности размножающейсреды на критичность реактора. Критический
радиус и критический объем сферы
Rкр
( K 1)
L, Vкр
4 3
Rкр , M кр топл Vкр .
3
• Предположим, что плотность размножающей
среды изменилась, а соотношение топлива и
замедлителя осталось неизменным C зам топл
• коэффициент размножения при этом не должен
измениться
23. Сферический реактор
Kf
a
f топл
(топл)
топл (зам)
C топл
a
a
f
(топл)
(зам)
C
a
a
• Изменится величина длины диффузии
L
D
1
1
1
a
3 tr a 3 tr a
1
3
• Таким образом L 1 а
• Учитывая, что ρ γ , получим Мкр 1/ γ2 .
• Так, например, если плотность ядерного
материала увеличить в два раза, то критическая
масса уменьшится в четыре раза
Vкр
24. Эффективный коэффициент размножения
• Для ограниченных размножающих сред такжеможно ввести понятие коэффициента
размножения, так называемый эффективный
коэффициент размножения .
• Рассмотрим некритическую среду. Некритичность
связана с тем, что нарушен баланс между числом
генерируемых реакцией деления нейтронов
• f f Ф и поглощением и утечкой нейтронов из
активной зоны D Ф Ф .
a
25. Эффективный коэффициент размножения
• Для сохранения баланса разделим источникнейтронов на некоторое число Кэф. Для
критического реактора Кэф=1. Для
подкритического Кэф<1, а для надкритического
Кэф>1.
D Ф a Ф
f f Ф
K ef
0
• Такой реактор называется условно критическим
K
D 1 a 0
K ef
26. Эффективный коэффициент размножения
Запишем условие критичности для этого реактора2
K эф
K K эф 1
L2
K
1 02 L2
02
эффективный коэффициент размножения учитывает
не только размножающие свойства среды, но и
форму, и размеры активной зоны реактора.
Для бесконечного реактора 2 0, K K
0
эф
27. Эффективный коэффициент размножения
проинтегрируем уравнение условно-критическогореактора по объему активной зоны
I Na
K
Na 0
K эф
где I - утечка нейтронов из реактора, равная числу
нейтронов, покидающих активную зону реактора в
единицу времени:
D ФdV D ФdV JdS I
Vаз
N a a ( r )dV
Vаз
Sаз
-скорость поглощения, равная числу
нейтронов, поглощенных в активной зоне в единицу
времени
Vаз
28. Эффективный коэффициент размножения
• K N a N f - скорость генерации нейтронов• Из этого баланса выразим эффективный
коэффициент размножения:
K эф
Nf
Nf
Na
K Pa
Na I Na Na I
N
a
Pa вероятность нейтрону,
• где N f K а
Na I
Na
• рожденному в активной зоне, поглотится в ней.
Pa
1
1 02 L2
29. Эффективный коэффициент размножения
• в активной зоне условно-критического реактора, вкотором , скорость рождения нейтронов равно
скорости поглощения и утечки нейтронов Кэф=1
• В общем случае
K эф
K
1 02 L2




























 physics
physics








