Методы решения геометрических задач

1. Методы решения геометрических задач

Учитель математики
МАОУ «СОШ № 146»
Манцирина Е.Е.

2.

Для решения сложных геометрических
задач, следует научить учеников
распознавать в них совокупность
простейших задач и опорных свойств
геометрических конструкций.

3. Точка на окружности

Опорные свойства:
Теорема о вписанном угле и следствия
Теорема об угле между касательной и
хордой
Теорема синусов
Вписанные и описанные многоугольники
(свойства и признаки)

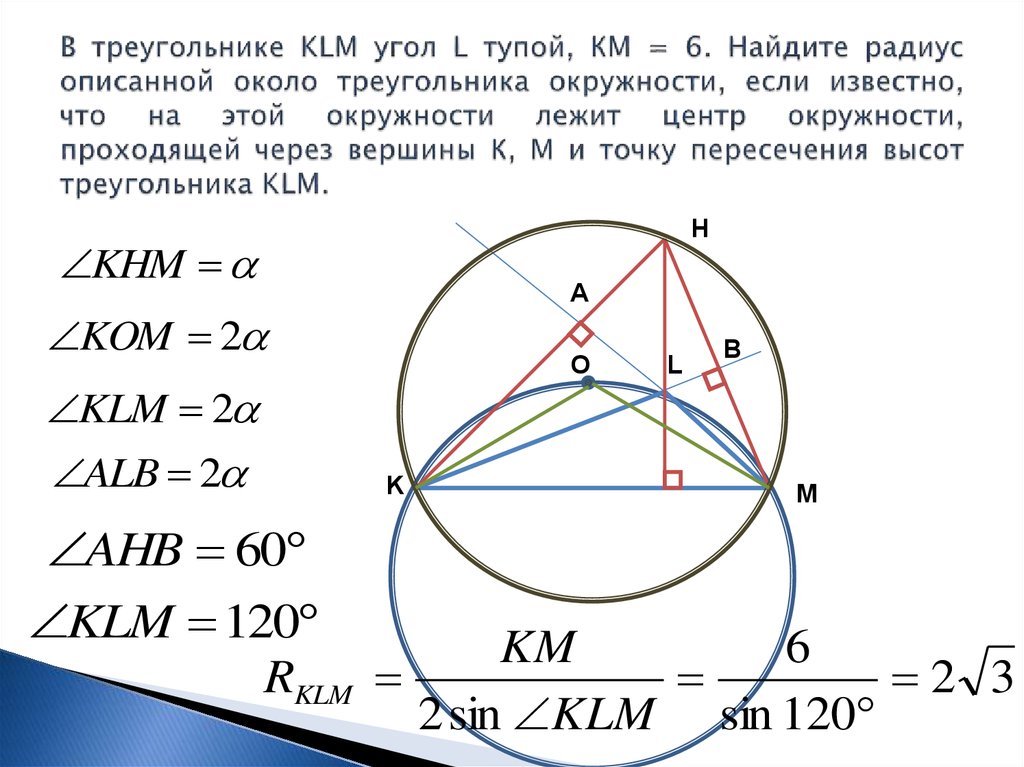
4. Задача 1. В треугольнике KLM угол L тупой, КМ = 6. Найдите радиус описанной около треугольника окружности, если известно, что

5. В треугольнике KLM угол L тупой, КМ = 6. Найдите радиус описанной около треугольника окружности, если известно, что на этой

H
KHM
A
KOM 2
O
KLM 2
ALB 2
K
AHB 60
KLM 120
RKLM
L
B
M
KM
6
2 3
2 sin KLM sin 120

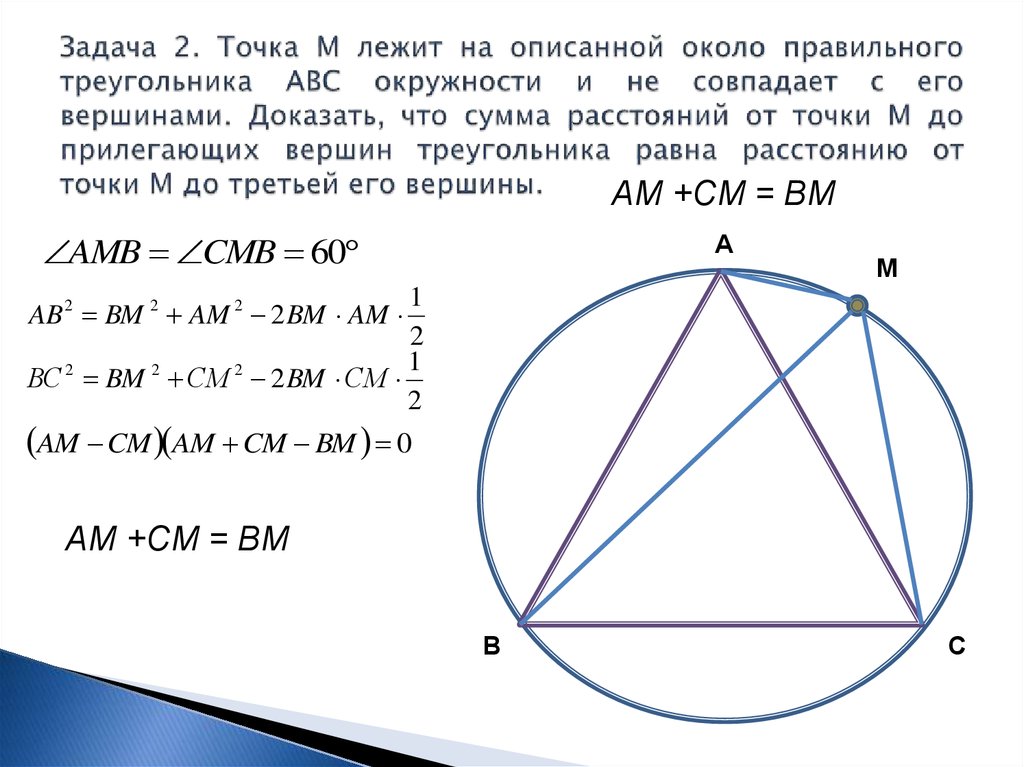
6. Задача 2. Точка М лежит на описанной около правильного треугольника АВС окружности и не совпадает с его вершинами. Доказать,

7. Задача 2. Точка М лежит на описанной около правильного треугольника АВС окружности и не совпадает с его вершинами. Доказать,

АМ +СМ = ВМ
AMB CMB 60
А
М
1
2
1
ВС 2 BM 2 СM 2 2 BM СM
2
AB 2 BM 2 AM 2 2 BM AM
AM CM AM CM BM 0
АМ +СМ = ВМ
В
С

8. Задача 3. В четырехугольнике ABCD, вписанном в окружность, стороны АВ и ВС равны соответственно 2 и 5, а стороны AD, CD и

BD = AB + ВС = 7
В
С
А
D

9. Задача 4. Диагонали выпуклого четырехугольника АВСD пересекаются в точке Е, AB = AD, СА – биссектриса угла С. Найти угол CDB,

BAD 140 , BEA 110 .
BCD 180 BAD 180 140 40
С
ABD ACD
1
1
BCD 40 20
2
2
CDB CAB EAB
180 ( ABD BEA)
180 (20 110 ) 50
E
В
D
А

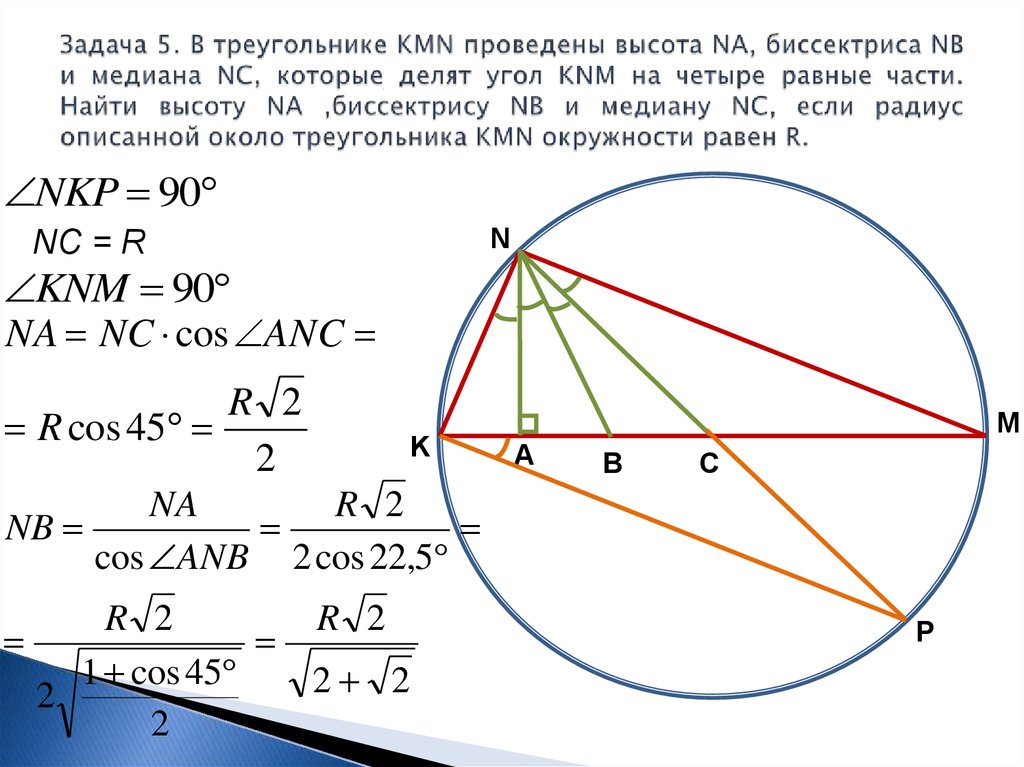
10. Задача 5. В треугольнике KMN проведены высота NA, биссектриса NB и медиана NC, которые делят угол KNM на четыре равные части.

NKP 90
N
NC = R
KNM 90
NA NC cos ANC
R 2
R cos 45
2
K
M
A
B
C
NA
R 2
NB
cos ANB 2 cos 22,5
R 2
R 2
1 cos 45
2 2
2
2
P

11. Литература

Шарыгин И.Ф. Геометрия. Планиметрия. М.:
Дрофа, 2001
Гордин Р.К. Геометрия. Планиметрия 7 – 9
классы. М.:МЦНМО, 2008
Бутузов В.Ф., Кадомцев С.Б., Э.Г. Позняк, С.А.
Шестаков, И.И. Юдина. Планиметрия. Пособие
для углубленного изучения математики. М.:
ФИЗМАТЛИТ, 2005
Алексеев В.Б., Панферов В.С., Тарасов В.А.
Избранные задачи по геометрии. Окружность. М.:
Илекса, 2012
Куланин Е.Д. Задачи по геометрии. М.: Илекса,
2012