Similar presentations:
Основные гипотезы линейной теории упругости
1. Основные гипотезы линейной теории упругости
1.2.
3.
4.
5.
Среда заполняет тело сплошным образом и не меняет свою
непрерывность в процессе приложения нагрузок.
До приложения нагрузок начальные напряжения в теле равны
нулю.
Напряжения в теле, возникающие после приложения
нагрузок, связаны линейной зависимостью с деформациями..
Перемещения тела малы по сравнению с линейными
размерами тела.
Относительные деформации и углы сдвига в материале малы
по сравнению с единицей
2. Принцип Сен-Венана
Если к малой части тела приложенасистема взаимно уравновешенных
нагрузок, то она вызывает лишь
местные напряжения, быстро
убывающие от места приложения
нагрузок
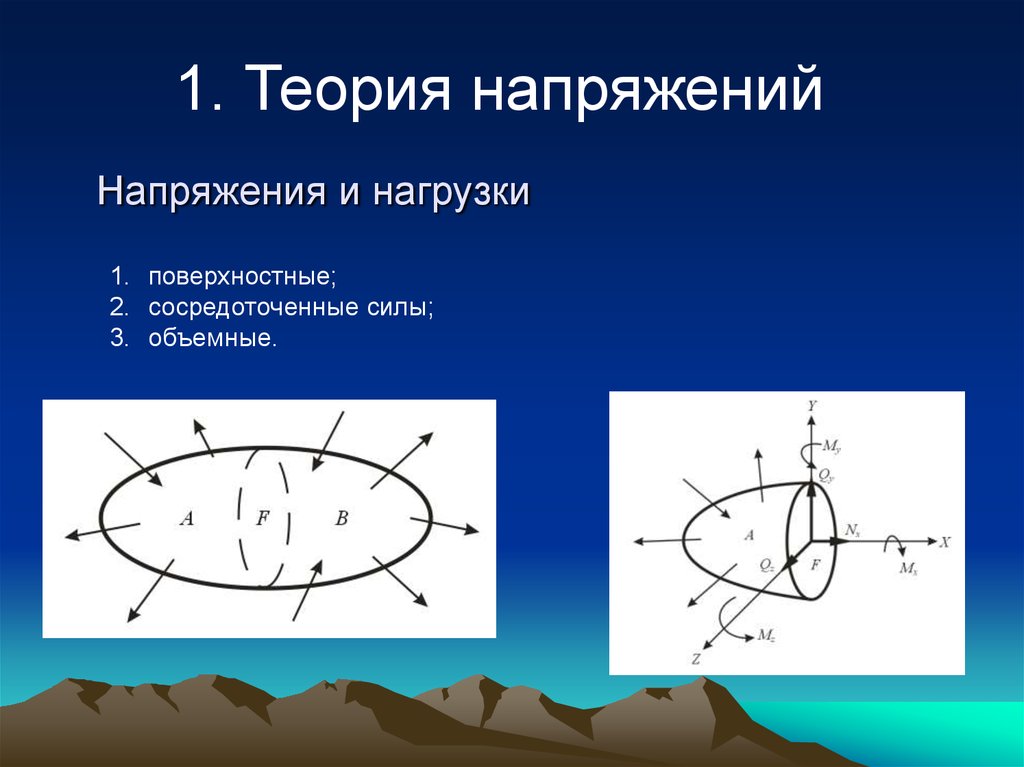
3. Напряжения и нагрузки
1. Теория напряженийНапряжения и нагрузки
1. поверхностные;
2. сосредоточенные силы;
3. объемные.
4. Составляющие полного вектора напряжений
tf 0 f
Pn lim
Составляющие полного вектора напряжений
t
Pn lim
f 0 f
5. Напряжения на наклонной площадке
Нормальное напряжение считается положительным, если оно вызывает растяжениеи в этом случае его направление совпадает с направлением внешней нормали к
площадке.
Касательные напряжения положительны, если внешняя нормаль к площадке
совпадает с направлением координатной оси (положительным или отрицательным
соответственно), а направлены они в сторону соответствующей этому направлению
координатной оси (положительной или отрицательной соответственно).
6. Напряжения на наклонной площадке
11
1
dydz x dxdz yx dxdy zx dfPnx 0
2
2
2
1
dydz df cos( n, x)
2
1
dxdz df cos( n, y )
2
1
dxdy df cos( n, z )
2
Pnx x cos( n, x) yx cos( n, y ) zx cos( n, z )
7. Граничные условия
nx cos( n, x), n y cos( n, y ),nz cos( n, z )
Pnx x nx yx n y zx nz
Pny xy nx y n y zy nz
Pnx xz nx yz n y z nz
8. Напряжения на наклонной площадке
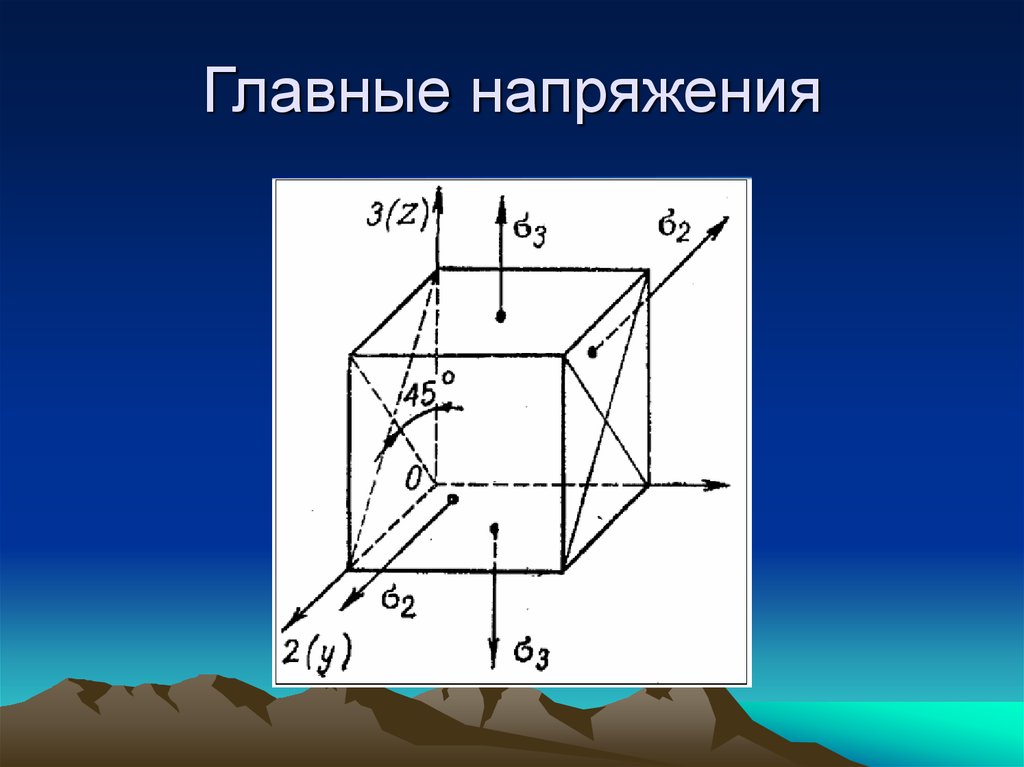
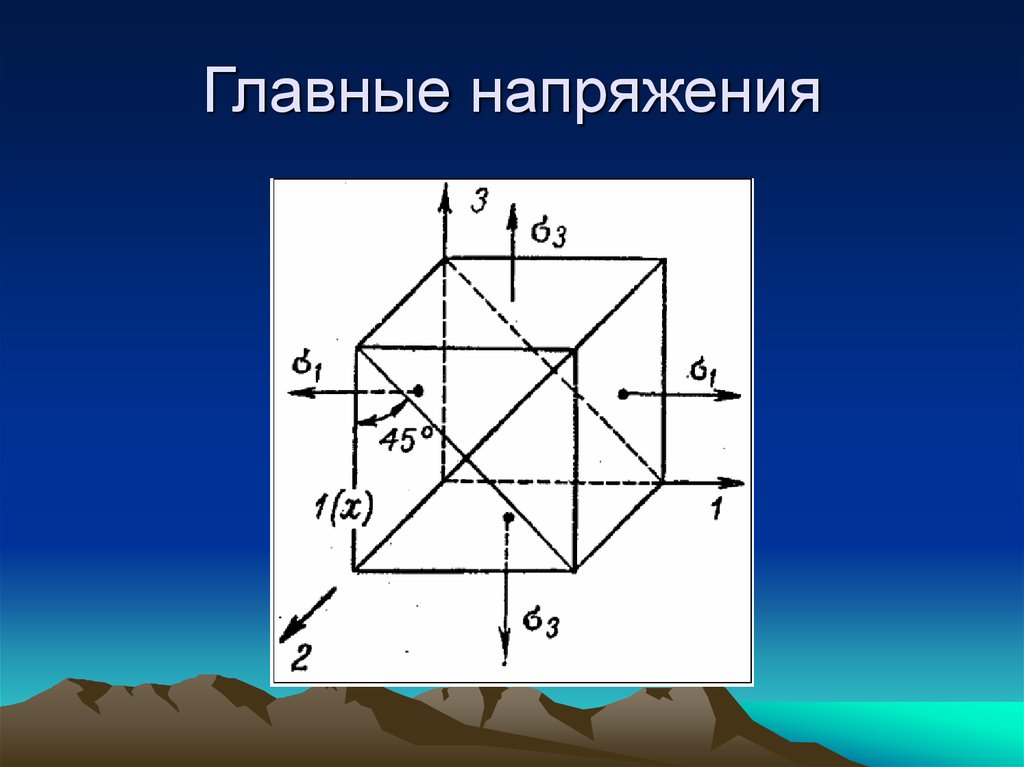
9. Главные напряжения
Главными называются такие площадки, на которыхдействуют только нормальные напряжения , а касательные
равны нулю.
Pnx n nx
n3 I1 n2 I 2 n I 3 0
I1 x y z
Pny n n y
Pnz n nz
x n nx yx n y zx nz 0
xy nx y n n y zy nz 0
I 2 x y y z z x xy2 yz2 zx2
xz nx yz n y z n nz 0
I 3 x y z 2 xy yz zx x yz2 y zx2 z xy2
x n
nx2 n y2 nz2 1
xy
xz
yx
zx
y
zy
n
yz
z n
0
1 2 3
10. Главные напряжения
11. Напряжения
12. Главные напряжения
13. Тензор напряжений
14. Главные напряжения
15. Главные напряжения
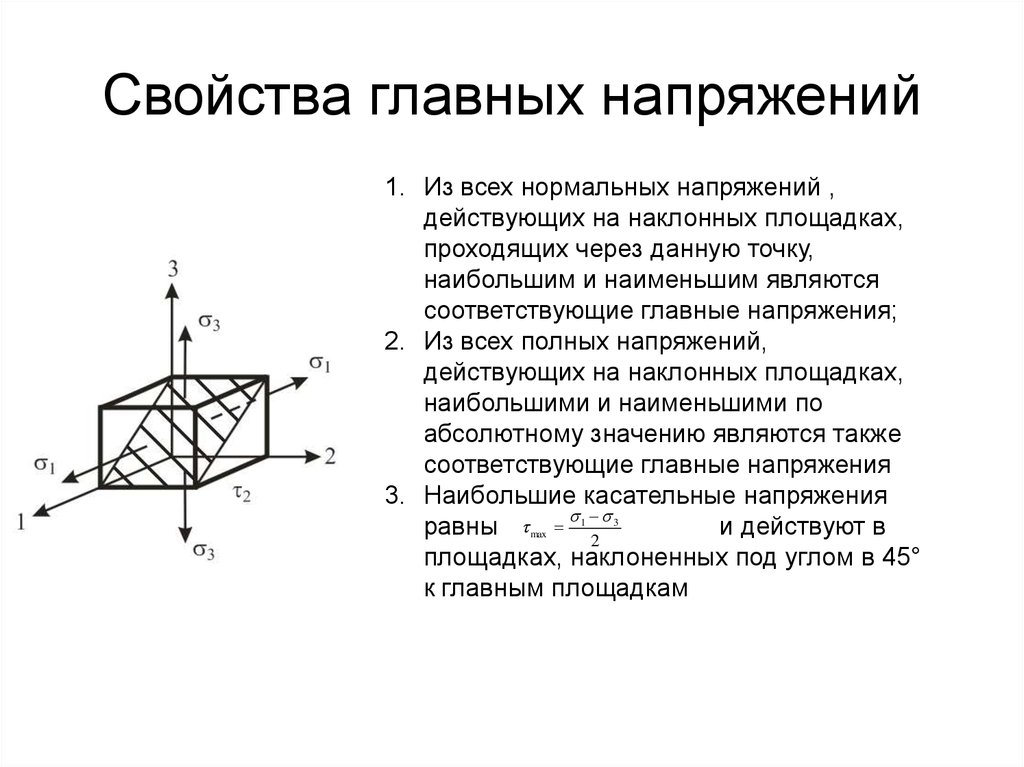
16. Свойства главных напряжений
1 Pn 31. Из всех нормальных напряжений ,
действующих на наклонных площадках,
проходящих через данную точку,
наибольшим и наименьшим являются
соответствующие главные напряжения;
2. Из всех полных напряжений,
действующих на наклонных площадках,
наибольшими и наименьшими по
абсолютному значению являются также
соответствующие главные напряжения
3. Наибольшие касательные напряжения
равны 2
и действуют в
площадках, наклоненных под углом в 45°
к главным площадкам
1
max
3
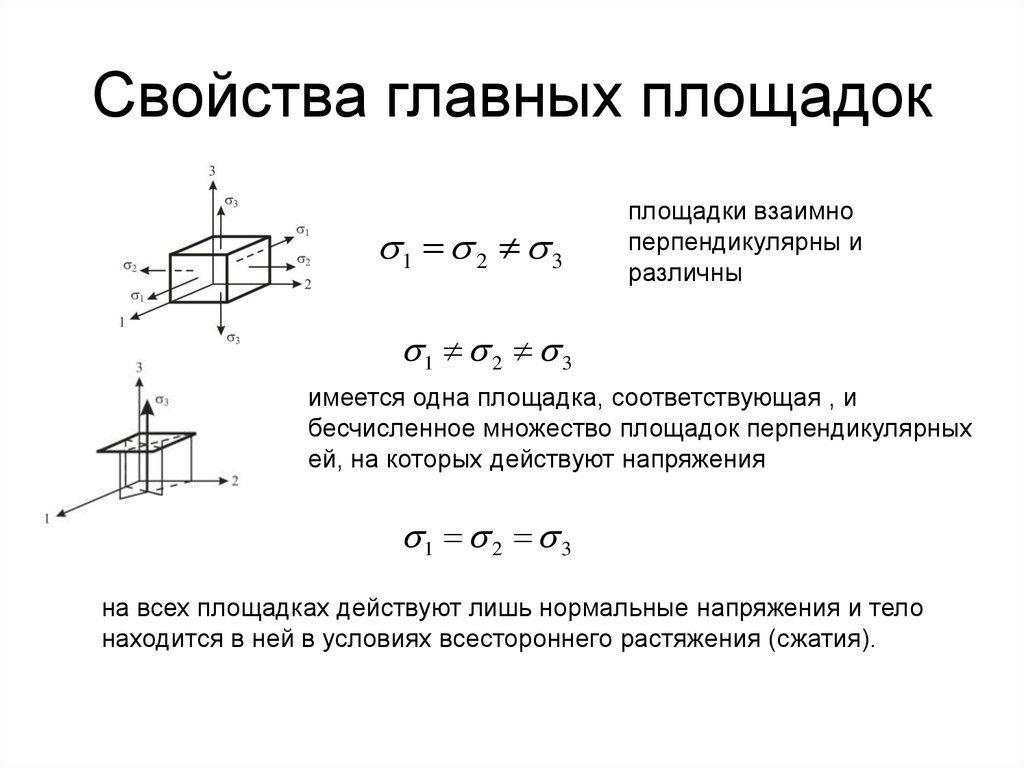
17. Свойства главных площадок
1 2 3площадки взаимно
перпендикулярны и
различны
1 2 3
имеется одна площадка, соответствующая , и
бесчисленное множество площадок перпендикулярных
ей, на которых действуют напряжения
1 2 3
на всех площадках действуют лишь нормальные напряжения и тело
находится в ней в условиях всестороннего растяжения (сжатия).
18. Октаэдрические площадки
Площадки, равнонаклоненные к главным площадкам, называютсяоктаэдрическими, На них действуют средние напряжения.
1
ср 1 2 3
3
1
1 2 2 2 3 2 3 1 2
о
3
3
i
о
2
Интенсивность напряжения — приведенное расчетное напряжение
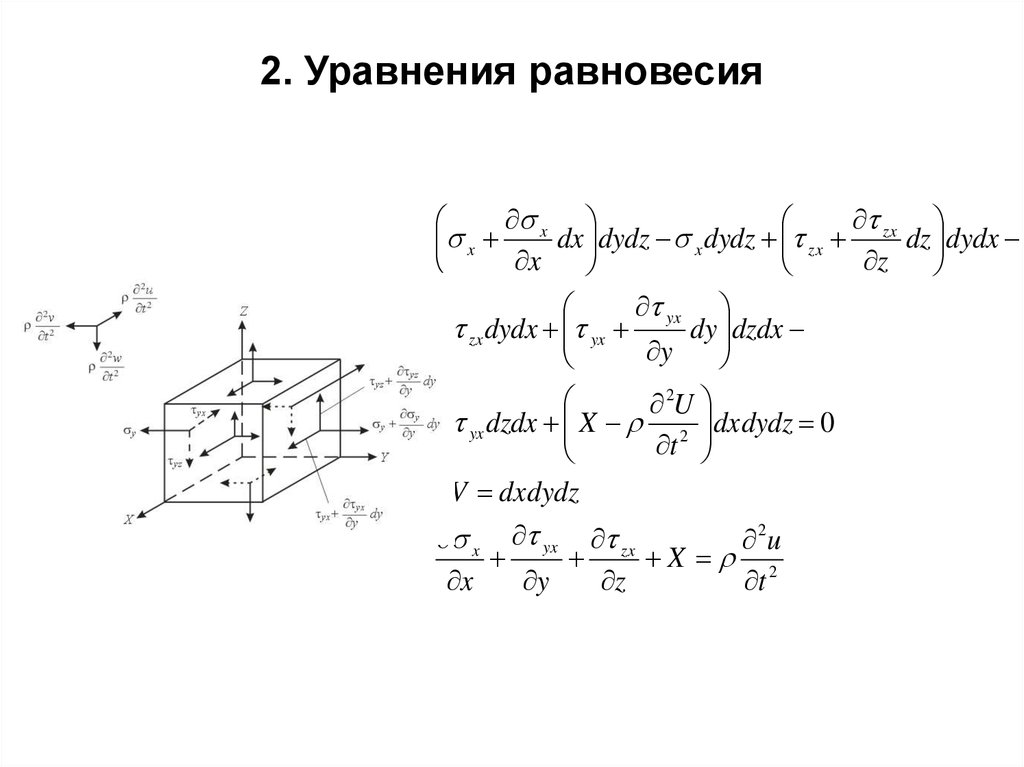
19. 2. Уравнения равновесия
xzx
dx
dydz
dydz
dz dydx
x
zx
x
x
z
yx
zx dydx yx
dy dzdx
y
2U
yx dzdx X 2 dxdydz 0
t
dV dxdydz
x yx zx
2u
X 2
x
y
z
t
20. Уравнения равновесия в проекции на оси координат
x yx zx0
x
y
z
xy y zy
0
x
y
z
xz yz z
0
x
y
z
21. Уравнения моментов относительно осей
Вычислим сумму моментов относительно оси X. Полагаем, чторавнодействующая внутреннего усилия, соответствующего
рассматриваемому напряжению, находится в центре грани
параллелепипеда
xy
dy
dz
dy
dz
xy dydz xz xz dx dydz xy
dx dydz
2
2
x
2
x
2
zy
dy
dy
z dydx z z dz dydx zy
dz dydxdz
2
z
2
z
y
yz
dz
y
dy dzdx yz
dy dzdxdy
y
2
y
dz
dy
dz
y dzdx Zdxdydz Ydxdydz
2
2
2
2v
dz
2w
dy
2 dxdydz 2 dxdydz 0
t
2
t
2
xz dydz
22. Закон парности касательных напряжений
zy yzxz zx
xy yx
Компоненты касательных напряжений, расположенные в двух взаимно
перпендикулярных площадках равны по величине и направлены по
перпендикуляру к линии пересечения этих площадок. При этом оба
компонента направлены либо к линии пересечения, либо от нее.
23. Количество неизвестных
Количество неизвестных=9, но с учетом закона парностикасательных напряжений=6
Количество уравнений равновесия =3
Количество неизвестных превышает
число уравнений равновесия
Задачи теории упругости являются
статически неопределимыми
Дополнительные уравнения необходимо получить из
рассмотрения деформации тела.

















 mechanics
mechanics








