Виды трубопроводов

1. Лекции по гидродинамике Часть 2

Автор: Раинкина Лариса Николаевна
к. т. н., доцент
В производственных
процессах
Гидродинамика изучает
нефтегазопромыслового дела
законы движения жидкостей
используются
и перемещаются
и рассматривает
приложения
разнообразные
этих законов кжидкости:
решению нефти,
нефтепродукты,
химические
практических инженерных
реагенты,
задач вода, глинистые
растворы по различным системам
ЗАКОНЫ ГИДРОДИНАМИКИ - ОСНОВА
РАСЧЕТОВ В НЕФТЕГАЗОВОМ ДЕЛЕ!

2. Виды трубопроводов

Трубопроводы
Простые
Последовательное
соединение
Сложные
a
р1, z1
Q
0
р2, z2
0
b
c
Параллельное
соединение
Q
Q2
a
Простой трубопровод
не имеет ответвлений
Q2
Q1
Q1
Q= Q1+Q2; (pa-pb)1
=(pa-pb)2
b
Q=xQ1=Q2;
pa-pc=(pa-pb)+
+(pb-pc)

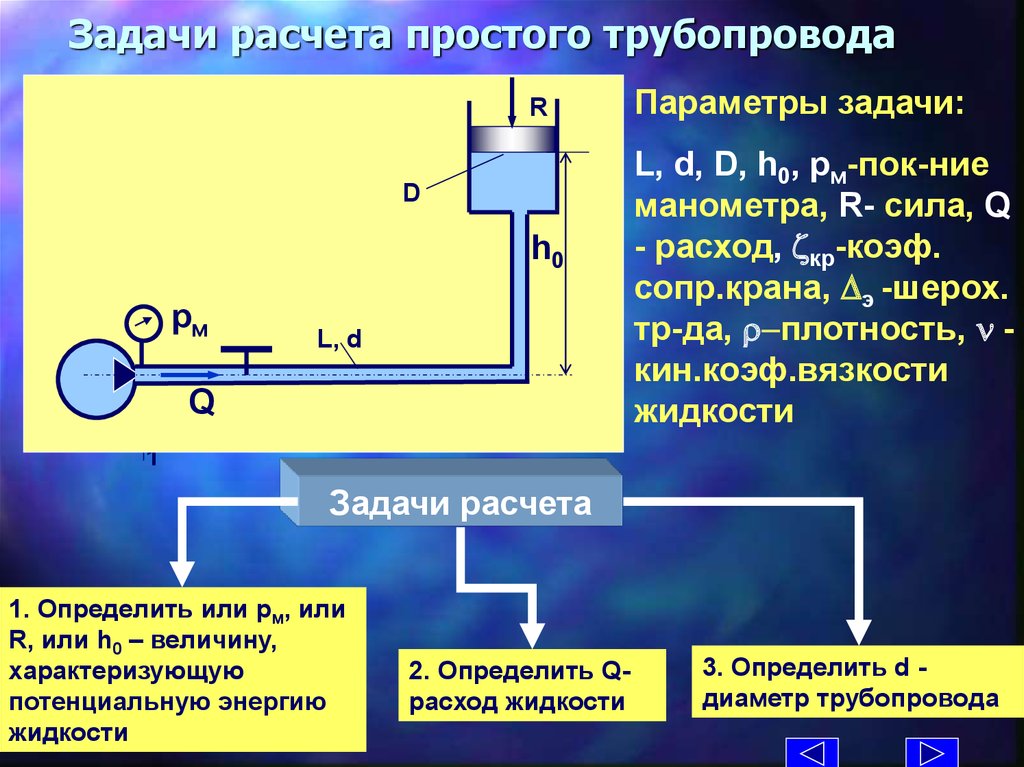
3. Задачи расчета простого трубопровода

Параметры задачи:
R
D
2
2
h0
1
рм
L, d
Q
0
0
L, d, D, h0, рм-пок-ние
манометра, R- сила, Q
- расход, zкр-коэф.
сопр.крана, э -шерох.
тр-да, r-плотность, n кин.коэф.вязкости
жидкости
1
Задачи расчета
1. Определить или рм, или
R, или h0 – величину,
характеризующую
потенциальную энергию
жидкости
2. Определить Qрасход жидкости
3. Определить d диаметр трубопровода

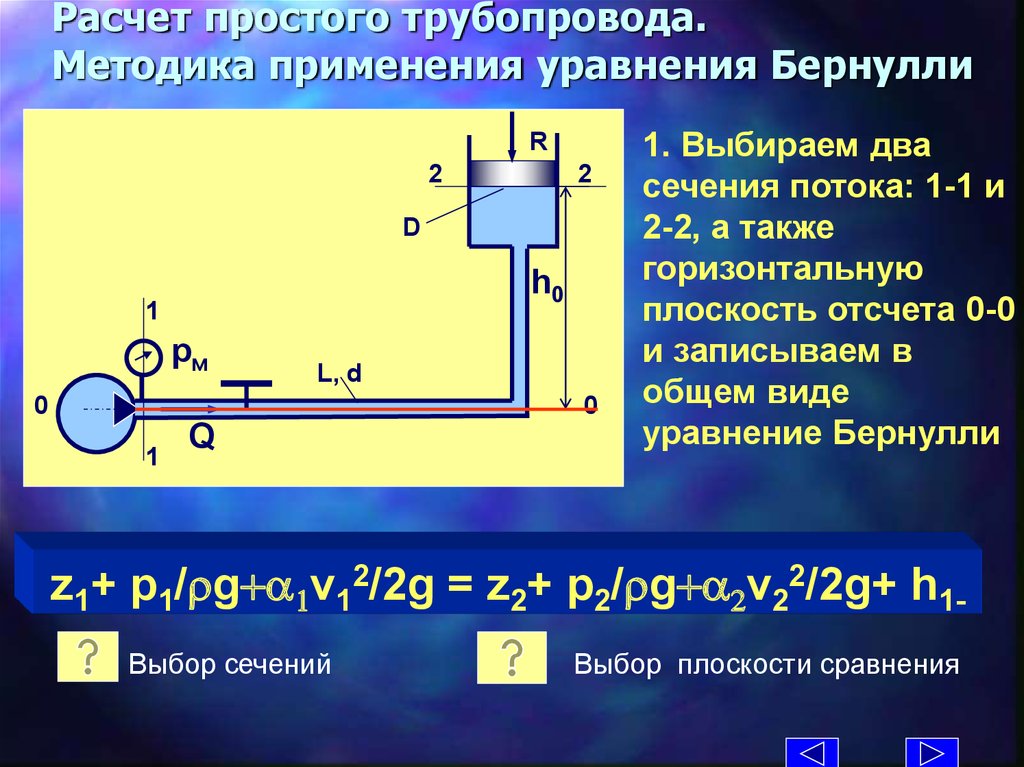
4. Расчет простого трубопровода. Методика применения уравнения Бернулли

R
2
2
D
h0
1
рм
L, d
0
0
1
Q
1. Выбираем два
сечения потока: 1-1 и
2-2, а также
горизонтальную
плоскость отсчета 0-0
и записываем в
общем виде
уравнение Бернулли
z1+ p1/rg+a1v12/2g = z2+ p2/rg+a2v22/2g+ h1Выбор сечений
2
Выбор плоскости сравнения

5. Правила выбора сечений и плоскости сравнения

Сечения выбираются всегда перпендикулярно
направлению движения жидкости и должны
располагаться на прямолинейных участках
потока
Одно из расчетных сечений необходимо брать
там, где нужно определить давление р, высоту z
или скорость J , второе, где величины р, z, и J
известны
Нумеровать расчетные сечения следует так,
чтобы жидкость двигалась от сечения 1-1 к
сечению 2-2
Плоскость сравнения 0-0 –любая горизонтальная
плоскость. Для удобства её проводят через центр
тяжести одного из сечений

6. Определение слагаемых уравнения Бернулли Z1 и Z2

z1+ p1/rg+a1v12/2g = z2+ p2/rg+a2v22/2g+ h12 R
2
2
Z1 =0
D
h0
1
рм
0
Z2 =h0
L, d
0
1
Q
Z–вертикальное расстояние от пл. 0-0 до центра тяжести сечения
Если сечение расположено выше 0-0 - +Z, если ниже 0-0 - Z

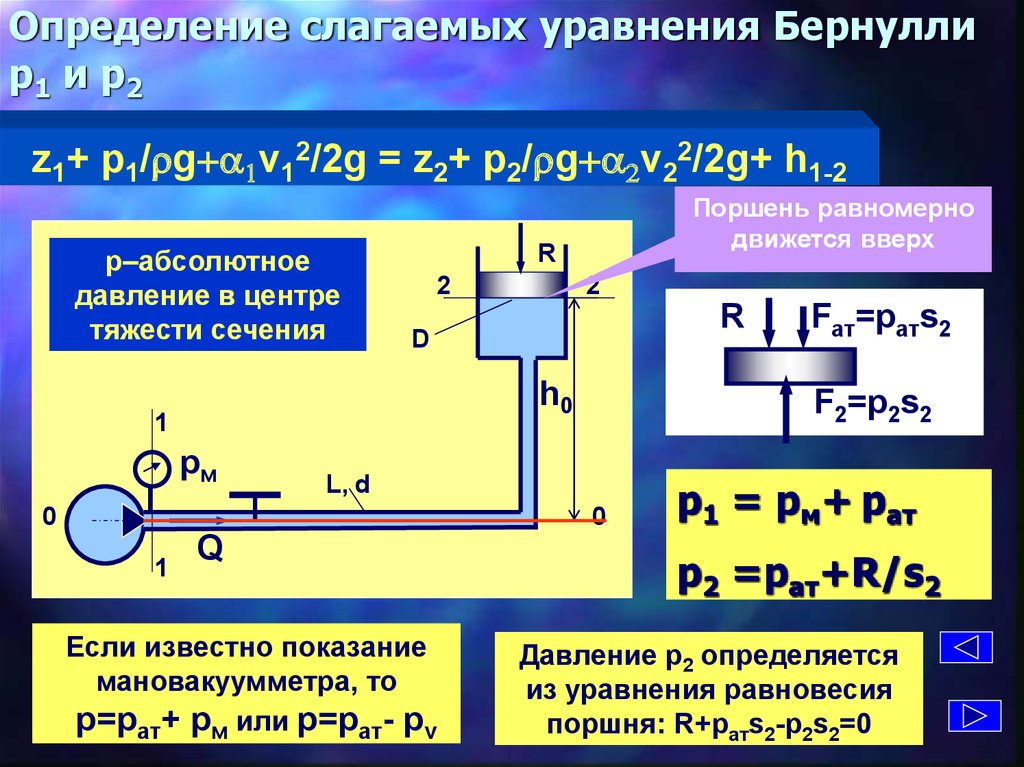
7. Определение слагаемых уравнения Бернулли p1 и p2

z1+ p1/rg+a1v12/2g = z2+ p2/rg+a2v22/2g+ h1-2
p–абсолютное
давление в центре
тяжести сечения
Поршень равномерно
движется вверх
R
2
2
R
D
h0
1
рм
F2=р2s2
L, d
0
0
1
Q
Если известно показание
мановакуумметра, то
р=рат+ рм или р=рат- рv
Fат=ратs2
р1 = рм+ рат
р2 =рат+R/s2
Давление р2 определяется
из уравнения равновесия
поршня: R+ратs2-p2s2=0

8. Определение слагаемых уравнения Бернулли v1 и v2

z1+ p1/rg+a1v12/2g = z2+ p2/rg+a2v22/2g+ h1-2
R
v–средняя скорость
в сечени потока
2
2
D
Q=v.s
1
рм
Расход жидкости один
и тот же во всех
сечениях потока
h0
L, d
0
0
1
Q
Средняя скорость
определяется через
расход жидкости
Если s2>> s1, то
v2<< v1
v1=Q/s1;
v2=Q/s2

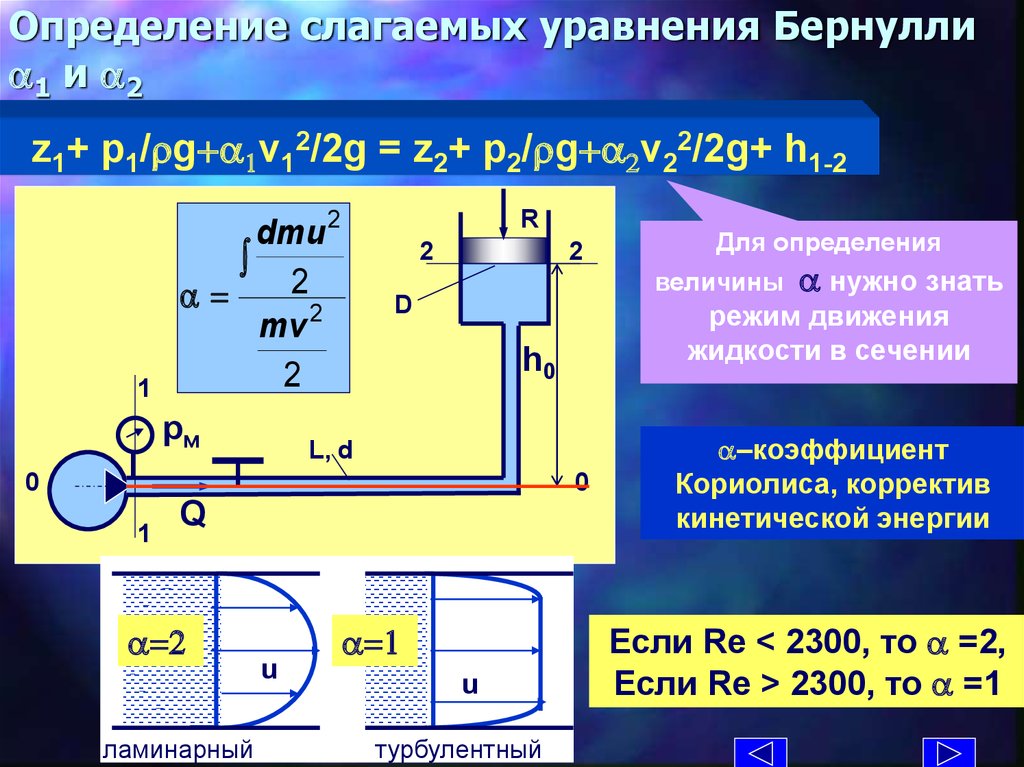
9. Определение слагаемых уравнения Бернулли a1 и a2

z1+ p1/rg+a1v12/2g = z2+ p2/rg+a2v22/2g+ h1-2
1
dmu 2
2
a=
mv 2
2
рм
R
2
2
величины
D
h0
0
0
Q
a=2
ламинарный
u
a=1
u
турбулентный
a нужно знать
режим движения
жидкости в сечении
L, d
1
Для определения
a–коэффициент
Кориолиса, корректив
кинетической энергии
Если Re < 2300, то a =2,
Если Re > 2300, то a =1

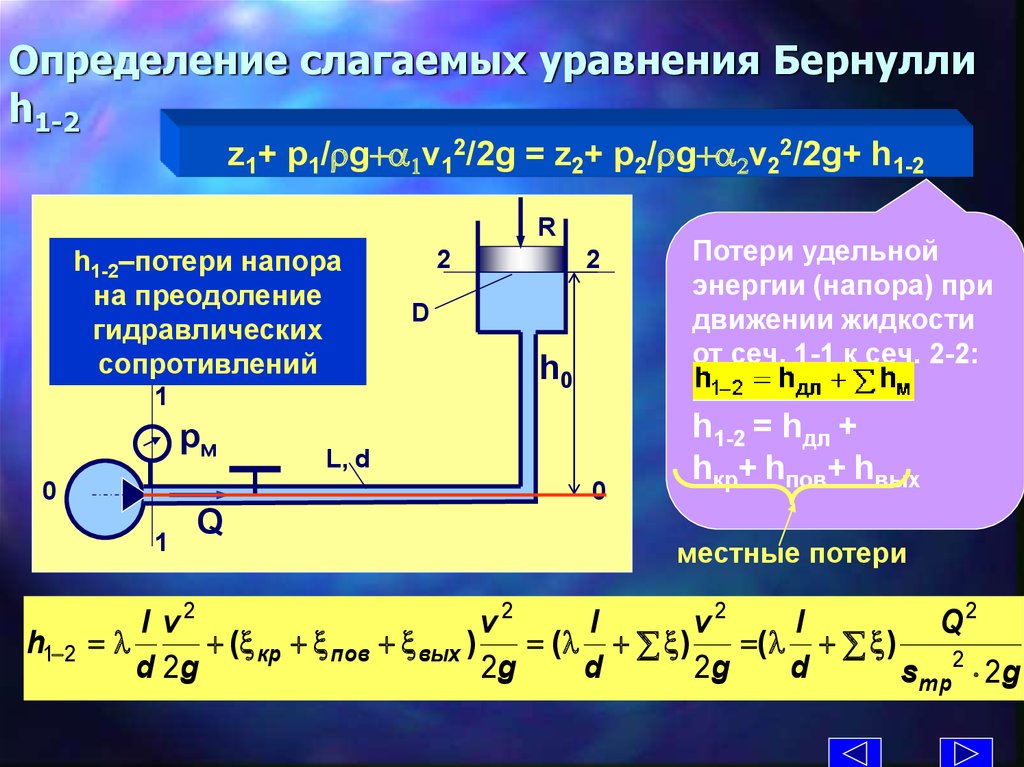
10. Определение слагаемых уравнения Бернулли h1-2

z1+ p1/rg+a1v12/2g = z2+ p2/rg+a2v22/2g+ h1-2
R
h1-2–потери напора
на преодоление
гидравлических
сопротивлений
1
рм
0
2
D
h0
L, d
0
1
h1- 2
2
Q
Потери удельной
энергии (напора) при
движении жидкости
от сеч. 1-1 к сеч. 2-2:
h1-2 = hдл +
hкр+ hпов+ hвых
местные потери
l v2
v2
l
v2
l
Q2
=
+ ( кр + пов + вых )
= ( + )
=( + )
d 2g
2g
d
2g
d
s тр2 2g

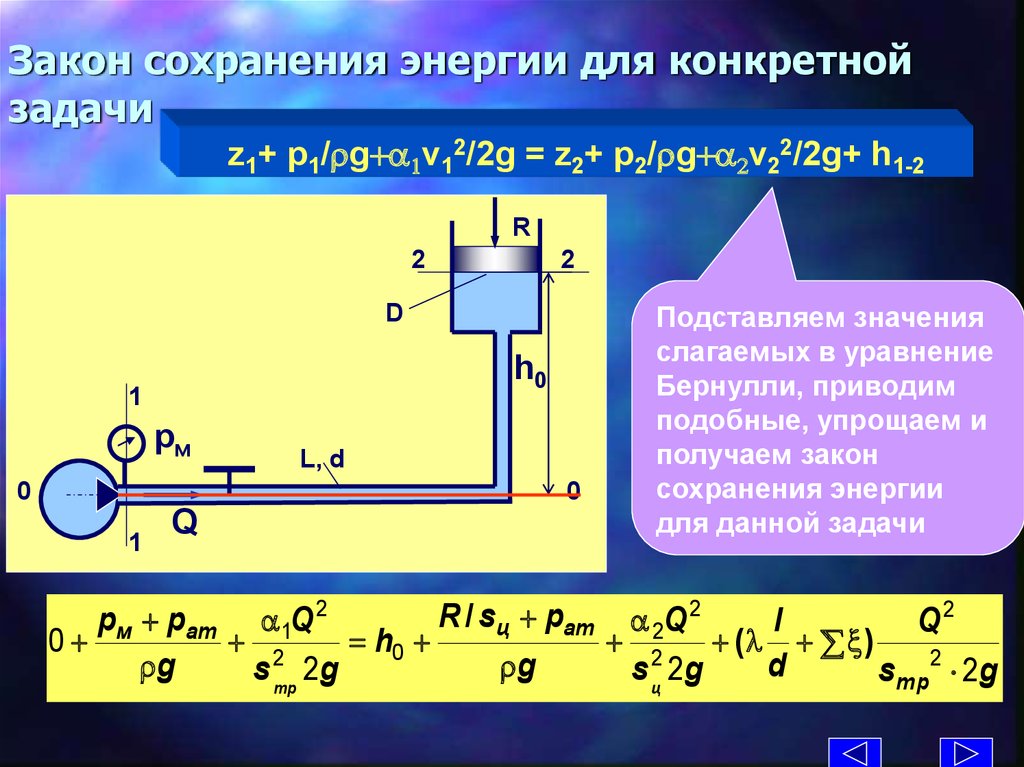
11. Закон сохранения энергии для конкретной задачи

z1+ p1/rg+a1v12/2g = z2+ p2/rg+a2v22/2g+ h1-2
R
2
2
D
h0
1
рм
0
L, d
0
1
Q
Подставляем значения
слагаемых в уравнение
Бернулли, приводим
подобные, упрощаем и
получаем закон
сохранения энергии
для данной задачи
R / sц + рат a 2Q 2
рм + рат a1Q 2
l
Q2
0+
+ 2
= h0 +
+ 2
+ ( + )
rg
rg
d
s тр 2g
s ц 2g
sтр2 2g

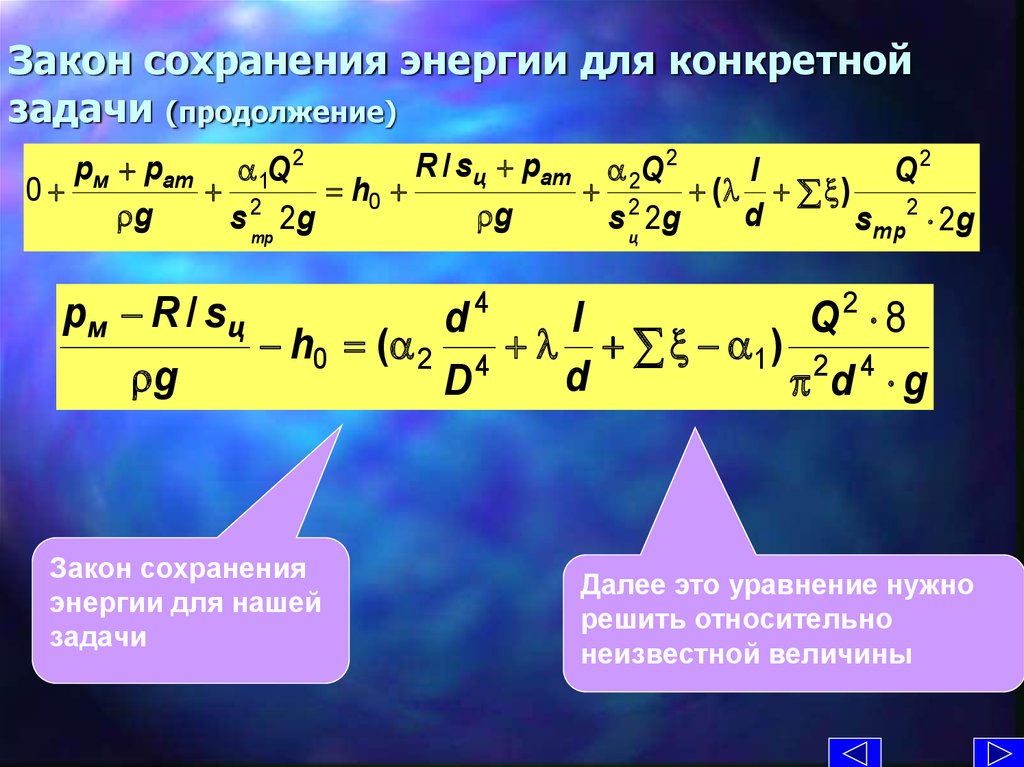
12. Закон сохранения энергии для конкретной задачи (продолжение)

R / sц + рат a 2Q 2
рм + рат a1Q 2
l
Q2
0+
+ 2
= h0 +
+ 2
+ ( + )
rg
rg
d
s тр 2g
s ц 2g
sтр2 2g
рм - R / s ц
rg
d4
l
Q2 8
- h0 = (a 2 4 + + - a 1 ) 2 4
d
D
d g
Закон сохранения
энергии для нашей
задачи
Далее это уравнение нужно
решить относительно
неизвестной величины

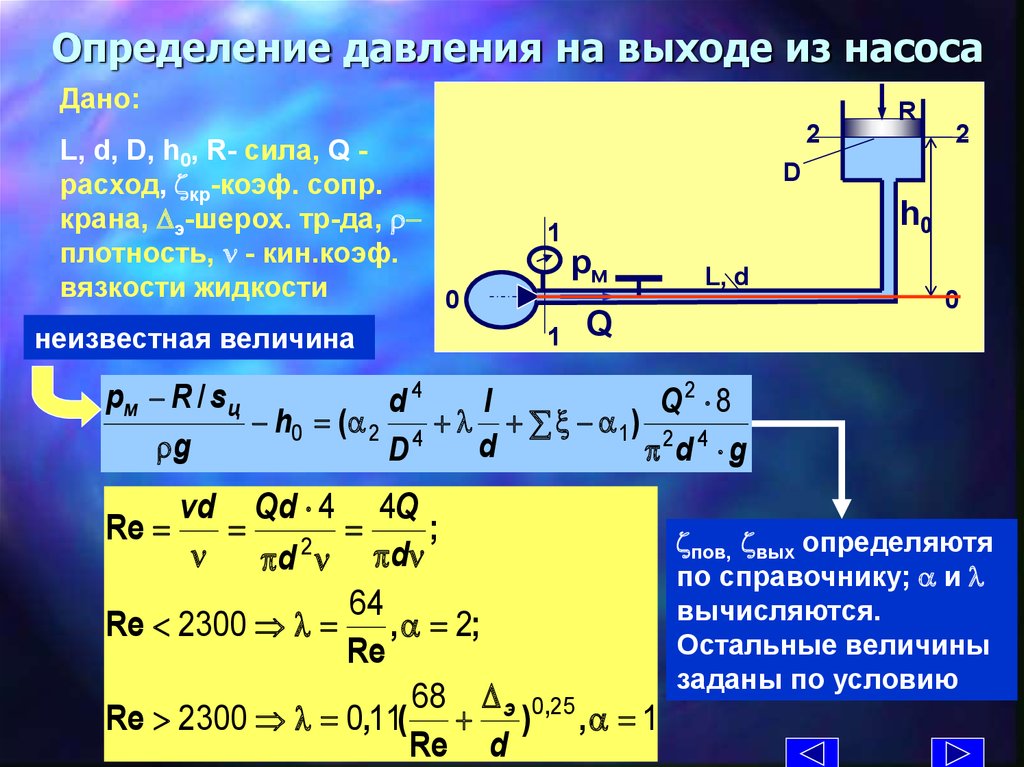
13. Определение давления на выходе из насоса

Дано:
L, d, D, h0, R- сила, Q расход, zкр-коэф. сопр.
крана, э-шерох. тр-да, rплотность, n - кин.коэф.
вязкости жидкости
0
неизвестная величина
рм - R / s ц
rg
2
2
D
1
1
h0
рм
L, d
Q
0
d4
l
Q2 8
- h0 = (a 2 4 + + - a1 ) 2 4
d
D
d g
vd Qd 4 4Q
=
=
;
2
n
d n dn
64
Re 2300 =
, a = 2;
Re
68 э 0,25
Re 2300 = 0,11( + ) , a = 1
Re d
Re =
R
zпов, zвых определяютя
по справочнику; a и
вычисляются.
Остальные величины
заданы по условию

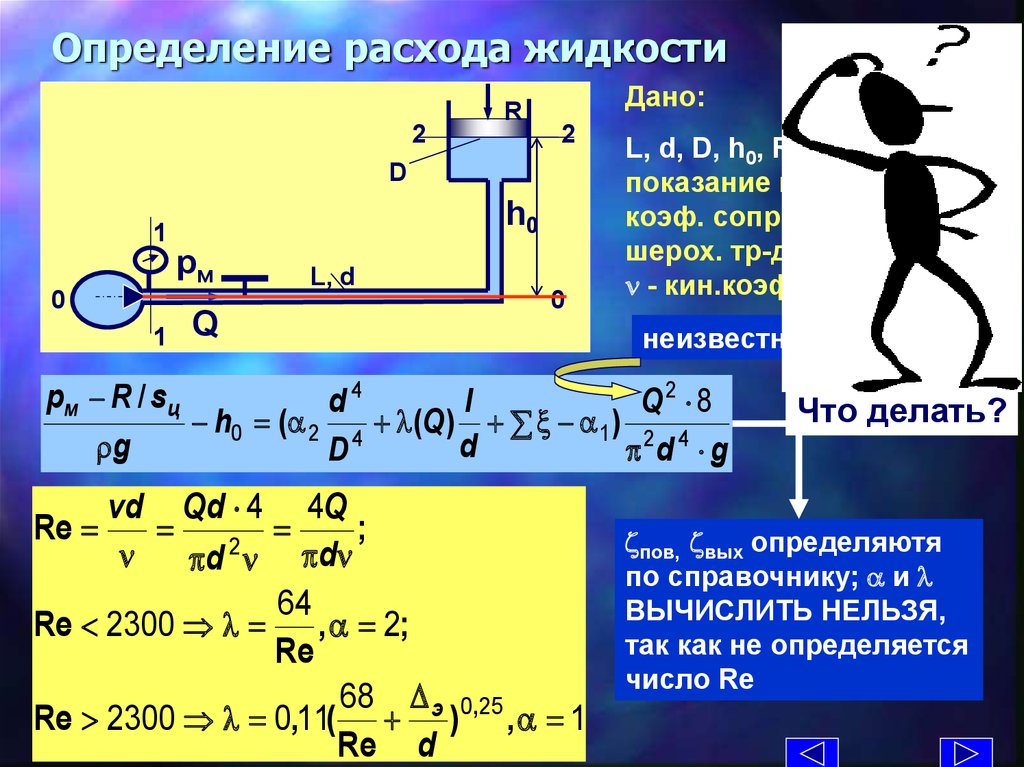
14. Определение расхода жидкости

2
R
Дано:
2
D
1
h0
рм
0
1
рм - R / s ц
rg
Q
L, d
0
неизвестная величина
d4
l
Q2 8
- h0 = (a 2 4 + (Q ) + - a1 ) 2 4
d
D
d g
vd Qd 4 4Q
=
=
;
2
n
d n dn
64
Re 2300 =
, a = 2;
Re
68 э 0,25
Re 2300 = 0,11( + ) , a = 1
Re d
Re =
L, d, D, h0, R- сила, рм –
показание манометра, zкркоэф. сопр. крана, эшерох. тр-да, r-плотность,
n - кин.коэф. вязкости жи
Что делать?
zпов, zвых определяютя
по справочнику; a и
ВЫЧИСЛИТЬ НЕЛЬЗЯ,
так как не определяется
число Re

15. Графический способ определения Q

рм - R / s ц
rg
d4
l
Q2 8
- h0 = (a 2 4 + (Q ) + - a1 ) 2 4
d
D
d g
F1(Q)
F2(Q)
F2(Q)
Трансцендентное уравнение (от
лат. transcendo-выхожу за
пределы). Это уравнение не
решается алгебраическими
способами
F1(Q)
Re =
F(Q)
Qр
Q
Q Re , a F2 (Q )
vd Qd 4 4Q
=
=
;
2
n
d n dn
64 dn
Re 2300 =
, a = 2;
4Q
68 dn э 0,25
Re 2300 = 0,11(
+ ) , a =1
4Q
d

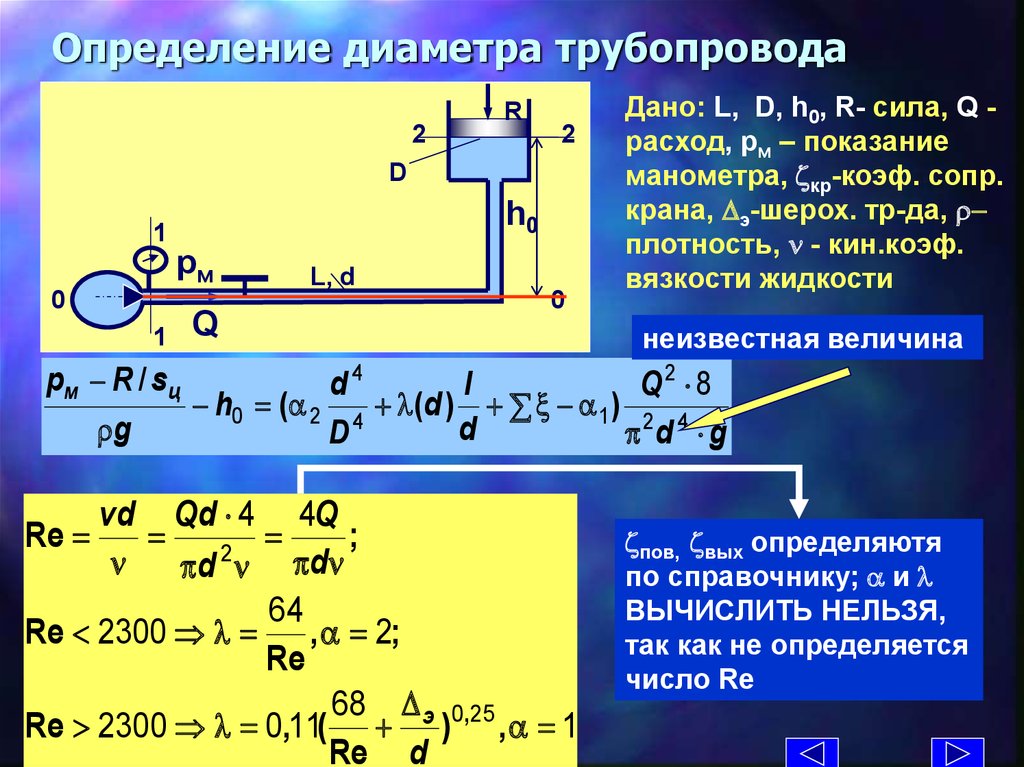
16. Определение диаметра трубопровода

2
R
2
D
1
h0
рм
0
1
рм - R / s ц
rg
Q
L, d
0
Дано: L, D, h0, R- сила, Q расход, рм – показание
манометра, zкр-коэф. сопр.
крана, э-шерох. тр-да, rплотность, n - кин.коэф.
вязкости жидкости
неизвестная величина
d4
l
Q2 8
- h0 = (a 2 4 + (d ) + - a1 ) 2 4
d
D
d g
vd Qd 4 4Q
Re =
=
=
;
2
n
d n dn
64
Re 2300 =
, a = 2;
Re
68 э 0,25
Re 2300 = 0,11( + ) , a = 1
Re d
zпов, zвых определяютя
по справочнику; a и
ВЫЧИСЛИТЬ НЕЛЬЗЯ,
так как не определяется
число Re

17. Графический способ определения d

рм - R / s ц
rg
d4
l
Q2 8
- h0 = (a 2 4 + (d ) + - a1 ) 2 4
d
D
d g
F1(d)
F2(d)
vd Qd 4 4Q
=
=
;
2
n
d n dn
64 dn
Re 2300 =
, a = 2;
4Q
68 dn э 0,25
Re 2300 = 0,11(
+ ) , a =1
4Q
d
Re =
F(d)
F2(d)
dр
F1(d)
d
d Re , a F2 (d )
Трансцендентное уравнение
относительно диаметра d

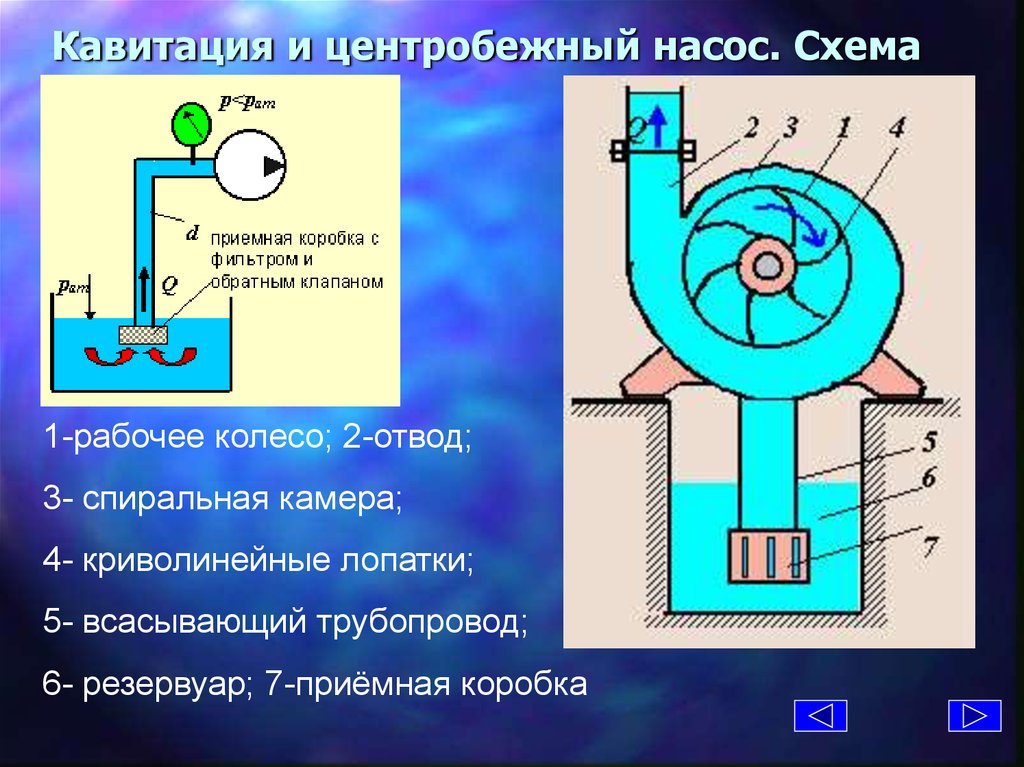
18. Кавитация и центробежный насос. Схема

1-рабочее колесо; 2-отвод;
3- спиральная камера;
4- криволинейные лопатки;
5- всасывающий трубопровод;
6- резервуар; 7-приёмная коробка

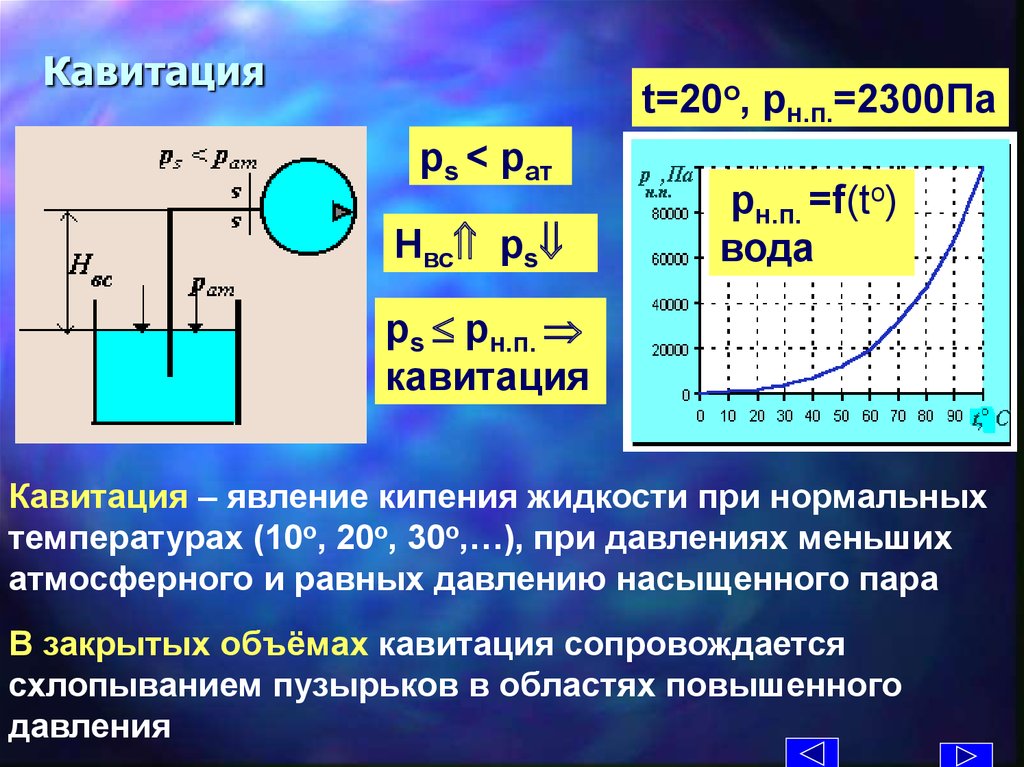
19. Кавитация

t=20o, pн.п.=2300Па
рs < pат
Hвс ps
pн.п. =f(to)
вода
рs pн.п.
кавитация
Кавитация – явление кипения жидкости при нормальных
температурах (10о, 20о, 30о,…), при давлениях меньших
атмосферного и равных давлению насыщенного пара
В закрытых объёмах кавитация сопровождается
схлопыванием пузырьков в областях повышенного
давления

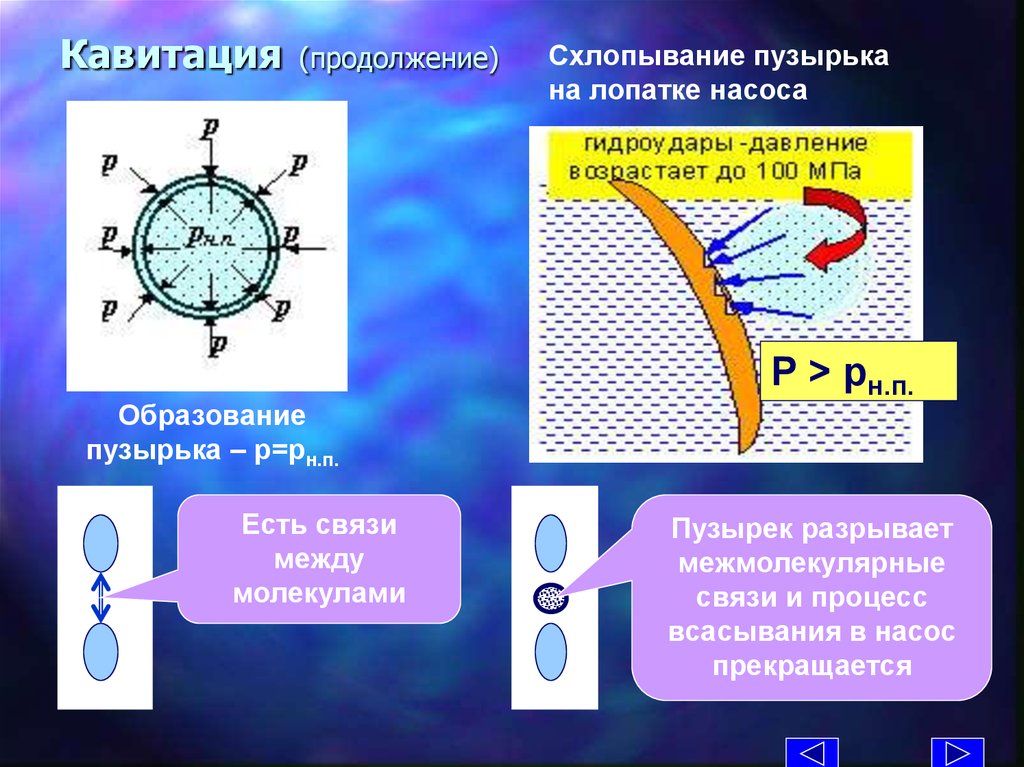
20. Кавитация (продолжение)

Образование
пузырька – р=рн.п.
Есть связи
между
молекулами
Схлопывание пузырька
на лопатке насоса
Р > pн.п.
Пузырек разрывает
межмолекулярные
связи и процесс
всасывания в насос
прекращается

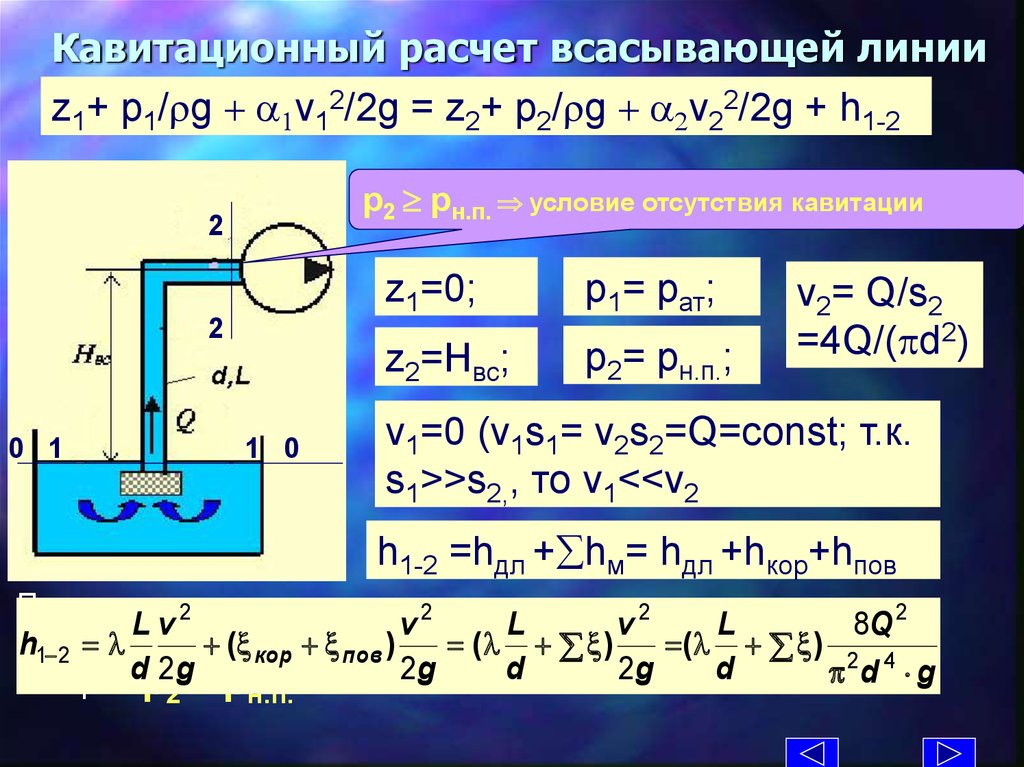
21. Кавитационный расчет всасывающей линии

z1+ p1/rg + a1v12/2g = z2+ p2/rg + a2v22/2g + h1-2
р2 pн.п. условие отсутствия кавитации
2
2
0 1
1 0
z1=0;
p1= pат;
z2=Hвс;
p2= pн.п.;
v2= Q/s2
=4Q/( d2)
v1=0 (v1s1= v2s2=Q=const; т.к.
s1>>s2,, то v1<<v2
h1-2 =hдл + hм= hдл +hкор+hпов
Применяем уравнение
2
L
v
Бернулли
h = для +сеч.
( 1-1+и
1- 2
2-2 при dр22g=
кор
pн.п.
v2
L
v2
L
8Q 2
= ( + )
= ( + ) 2 4
пов )
2g
d
2g
d
d g

22. Кавитационный расчет всасывающей линии

2
рат - рн .п .
L
8Q
- H вс = ( + + a 2 ) 2 4
rg
d
d g
Применяем уравнение Бернулли для
сеч. 1-1 и 2-2 при р2 = pн.п.
2
Задачи расчета
2
0 1
1 0
1. Определение максимальной
высоты подъёма (Hвс)max
2. Определение максимального
расхода Qmax
3. Определение минимального
диаметра трубопровода dmin

23. Графический способ определения Qmax

рат - рн .п .
L
8Q 2
- H вс = ( + + a 2 ) 2 4
rg
d
d g
F1(Q)
F2(Q)
F2(Q)
Трансцендентное уравнение (от
лат. transcendo-выхожу за
пределы). Это уравнение не
решается алгебраическими
способами
F1(Q)
Re =
F(Q)
Qр
Q
Q Re , a F2 (Q )
vd Qd 4 4Q
=
=
;
2
n
d n dn
64 dn
Re 2300 =
, a = 2;
4Q
68 dn э 0,25
Re 2300 = 0,11(
+ ) , a =1
4Q
d