Similar presentations:
Применение функций комплексного переменного
1. ГИДРОМЕХАНИКА
2.
Лекция 7Плоское потенциальное
движение
3.
Применение функций комплексного переменногоКак уже отмечали, для для плоских потенциальных течений существуют функции, связанные соотношениями
ux
;
х у
uу
у
х
Эти уравнения дают возможность применить
для описания потенциальных течений несжимаемой жидкости, аппарат теории функции
комплексного переменного
4.
Применение функций комплексного переменногоВ теории функций комплексного переменного
доказывается, что если две функции φ(х,у) и
ψ(х,у) связаны приведенными условиями
(условиями Коши-Римана), то они являются
соответственно действительной и мнимой
частью некоторой функции комплексного
переменного
w (z)= φ +iψ,
называемой комплексным потенциалом.
Эта функция обладает определенной конечной производной во всех точках области, где
определены φ и ψ .
5.
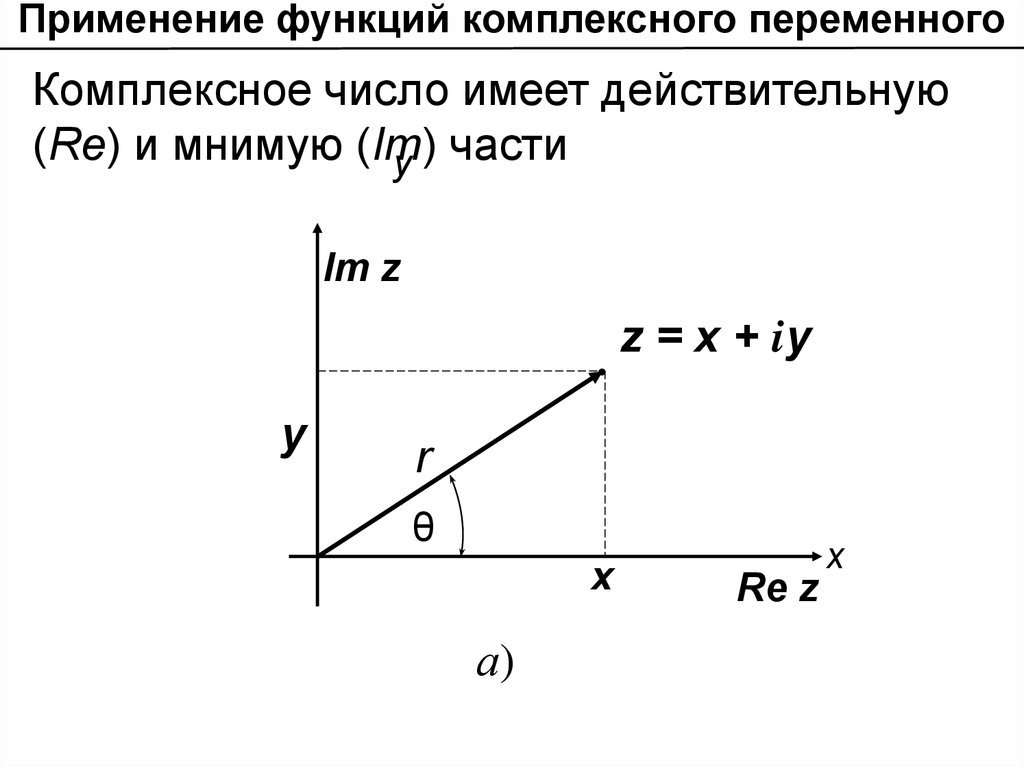
Применение функций комплексного переменногоКомплексное число имеет действительную
(Re) и мнимую (Im)
у части
Im z
z = x + iy
y
r
θ
x
а)
Re z
х
6.
Применение функций комплексного переменногоПлоскость течения рассматривается, как плоскость комплексной переменной z = x + iy
7.
Применение функций комплексного переменногоКомплексное число также можно изображать
радиус-вектором. Длина радиус-вектора, изображающего комплексное число , называется
модулем комплексного числа.
Модуль вычисляется по формуле:
r х у
2
2
8.
Применение функций комплексного переменногоО комплексных числах
Модуль любого ненулевого комплексного числа есть положительное число.
Число z = x - iy называется комплексно-сопряженным числом к числу z = x + iy , т. е.
комплексно сопряженные числа отличаются
лишь знаком мнимой части.
Модули комплексно-сопряженных чисел
равны.
9.
Применение функций комплексного переменногоМодуль произведения (частного) двух комплексных чисел равен произведению (частному) модулей каждого из чисел.
Аргумент θ комплексного числа связан с его
действительной и мнимой частями соотношениями:
y
arg z tg ;
x
10.
Применение функций комплексного переменногоcos
x
x y
2
2
; sin
y
x y
2
2
Тригонометрической формой комплексного
числа называется выражение
z r (cos isin )
Показательной формой комплексного числа
называется выражение
z rе
i
11.
Применение функций комплексного переменногоДля того, чтобы функция
w (z)= φ +iψ=φ(x,y)+iψ(x,y),
определенная в некоторой области, была
дифференцируемой в точке z этой области,
необходимо и достаточно, чтобы функции
φ(х, у) и ψ(x,y)
были дифференцируемы в той же точке и для
них удовлетворялись уравнения Коши-Римана.
ux
;
х у
uу
у
х
12.
Применение функций комплексного переменногоТакая функция называется аналитической.
Следовательно, любую аналитическую функцию w(z) можно рассматривать как комплексный потенциал некоторого плоского
течения.
Производная функции комплексного
переменного считается существующей
лишь тогда, когда
W dW
lim
dz
z 0 z
не зависит от способа приближения Δz
к нулю.
13.
Применение функций комплексного переменногоdW
W
W ( z z ) W ( z )
lim
lim
dz z 0 z z 0
z
( x x , y ) i ( x x , y ) ( x , y ) i ( x , y )
lim
z
x 0
d d
i u x iu y
dx dx
14.
Применение функций комплексного переменногоПроизводная комплексного потенциала по независимой переменной представляет собой
комплексную переменную
и u x iu y
действительная часть которой равна проекции
скорости иx, а мнимая – взятой с обратным
знаком проекции иу
15.
Применение функций комплексного переменногоПроизводная функции течения в какой либо
точке равна комплексной сопряженной
скорости в этой точке.
Модуль этой пpoизводной дает абсолютную
величину скорости, а аргумент, взятый с
обратным знаком, определяет направление
скорости в рассматриваемой точке.
При сложении течений комплексные потенциалы суммируются:
W(z) = W1(z) + W2(z) + …+Wn (z)
16.
Применение функций комплексного переменногоВ плоскости течения могут находиться точки, в
которых производная комплексного потенциала обращается в ноль или в бесконечность.
Это особые точки, в которых функция W(z) не
является аналитической.
В точках, где
dW
,
dz
может пересекаться бесконечно большое
число линий тока. В этих точках распoлагaютcя источники, диполи, вихри.
17.
Применение функций комплексного переменногоВ точках, где
dW
0,
dz
(и =0) пересекаются две или несколько (конечное число) линий тока. Эти точки называются
точками разветвления, а пpoходящиe через
них линии тока - разделительными.
18.
Применение функций комплексного переменногоВеличину и называют сопряженной скopостью. В комплексной плоскости иx, иу называемой плоскостью годографа скорости, число
является сопряженным с числом
u u x iu y ,
которое называется комплексной скоростью.
Величины и и
форме
и
можно также представить в
u u x iu y u (cos isin ) u e
i
u u x iu y u (cos isin ) u e
i
19.
Применение функций комплексного переменногоПлоские течения с помощью комплексного
потенциала можно изучать различно.
Во-первых, можно, задавшись конфигурацией
линий тока или полем скоростей, отыскивать
вид функций φ и ψ, W и и .
Во-вторых, можно, задавшись аналитической
функцией W, выделить в ней действительную
и мнимую части (т. е. φ и ψ).
А также найти
dW
dz
u
чем определится поле скоростей.
20.
Рассмотрим, как выразится комплексныйпотенциал для элементарных потоков.
21.
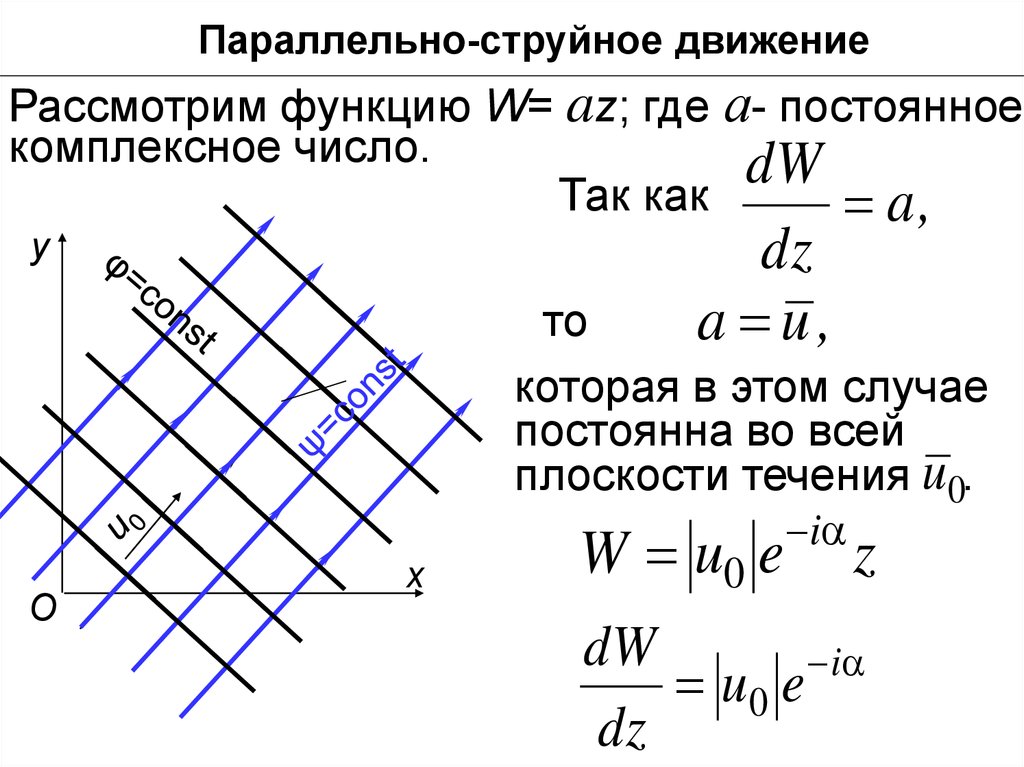
Параллельно-струйное движениеРассмотрим функцию W= az; где а- постоянное
комплексное число.
dW
Так как
a,
у
О
dz
a u,
х
то
которая в этом случае
постоянна во всей
плоскости течения u 0.
i
W u0 e z
dW
i
u0 e
dz
22.
Параллельно-струйное движениеW i
u0 x x u0 y y u0 ( xcos ysin )
u0 x y u0 y x u0 (- xsin ycos )
Вдоль линий тока ψ= const и, следовательно,
их уравнение запишется, в виде
u0 x y u0 y x const
Это уравнение семейства параллельных
прямых, наклоненных к оси х, под углом α
tg
u0 y
u0 x
23.
Параллельно-струйное движениеЭквипотенциали представляют собой дpyгoе
семейство параллельных прямых, ортогональное к первому.
В частном случае, когда и0у = 0 (α0 = 0),
будет
W = u0xz; и= и0х; φ = и0хх; ψ= и0ху
и получается прямолинейный поток вдоль
оси х.
Если же α = π/2, то этот поток направлен
вдоль оси у:
W = -iu0yz; и = iи0y; φ = и0yy; ψ= - и0yx
24.
Течение от источника (стока) в начале координатφ=const
ψ=const
dsθ
dr
dW
Q
dz
2 z
Q
W ln z
2
Представим z в показательной форме
i
z rе
тогда
Q
W (ln z i ) i
2
Q
Q
2
2
ln r ln x y
2
2
Q
Q
y
arctg
2
2
x
25.
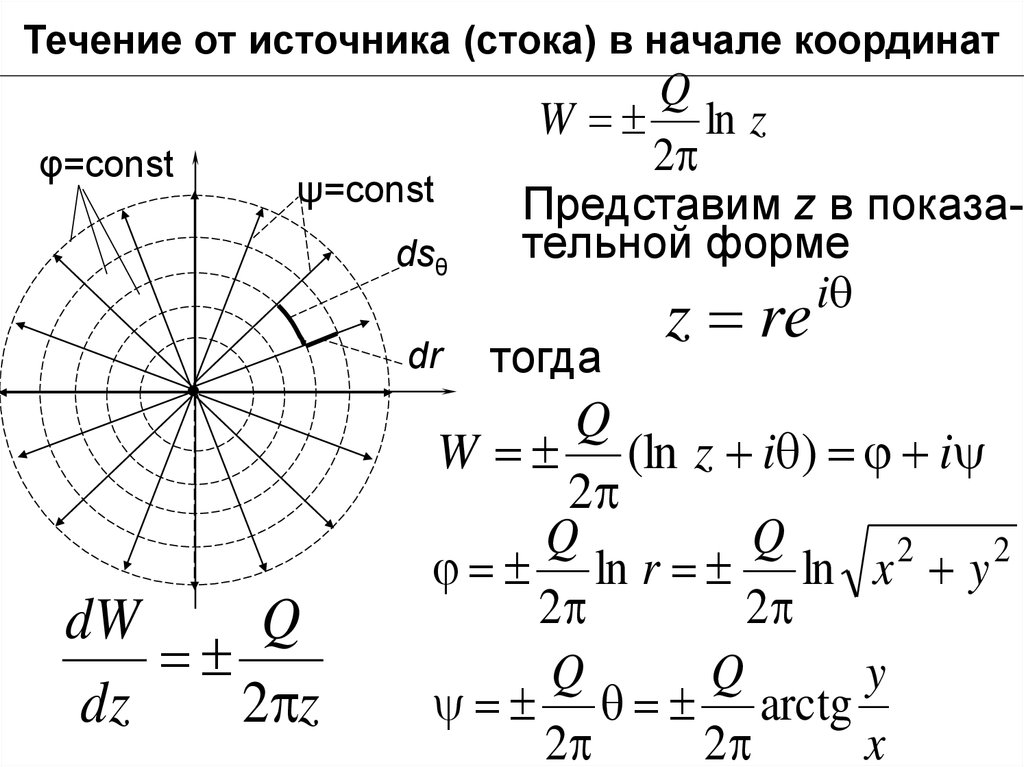
Течение от источника (стока) в начале координатЛинии тока (ψ= cоnst или у/х =const) представляют собой прямые, проходящие через начало
координат,
а
эквипотенциали
(φ=
const
или
х2+y2= const) -окружности с общим центром в
начале координат.
Проекции скорости в полярных координатах:
Q
1
ur
; u
0
r
2 r
s r
В поле источника (стока) скорость убывает обратно пропорционально расстоянию от центра.
Скорость, направленная от центра к
периферии (источник), положительна, в этом
случае Q >0. Стоку соответствует Q <0.
26.
Течение от источника в точке z0=x0+iy0y
φ=const
ψ=const
dr
y0
x0
Q
W ln( z z0 )
2
dW
Q
dz
2 ( z z0 )
x
Q
Q
2
2
ln r ln ( x x0 ) ( y y0 )
2
2
y y0
Q
Q
arctg
2
2
x x0
27.
Течение от вихря в точке z0=x0+iy0y
iГ
W ln( z z0 )
2
dW
iГ
dz
2 ( z z0 )
φ=const
ψ=const
y0
x0
x
y y0 Г
Г
arctg
2
x x0 2
Г
Г
2
2
ln ( x x0 ) ( y y0 ) ln r
2
2
28.
Течение от диполя в точке z0=x0+iy0y
Комплексный потенциал
М
1
W
2 ( z z 0 )
y0
dW
М
1
dz
2 ( z z 0 ) 2
x
x0
x x0
М
М cos
2 ( x x0 ) 2 ( y y 0 ) 2 2 r
y y0
М
М sin
2
2
2 ( x x0 ) ( y y 0 )
2 r

























 physics
physics








