Similar presentations:
Гипотезы в инженерном эксперименте – основа правильной интерпретации результатов эксперимента. Принцип Сен-Венана
1. Гипотезы в инженерном эксперименте – основа правильной интерпретации результатов эксперимента Принцип Сен-Венана
ExH
G xz
(1,5 2,0)H
Затухание возмущений в изотропном (а) и анизотропном (б) материале
(Н – характерный размер источника возмущения - для стержней – больший из размеров
поперечного сечения)
Растяжение
Изгиб
2. Определение характеристик упругости и прочности в направлении, перпендикулярном плоскости армирования и под углом 45О к ней
(углерод-углеродный КМ)на коротких образцах (длина 55 – 65 мм)
max ~ 2,5 МПа
Перпендикулярно ткани
max ~ 40 МПа
Под углом 45О к ткани
Определяемые хар-ки
поперек плоск. армир.:
модуль упругости,
модуль сдвига,
прочность при сжатии
и растяжении,
по прочности
на сжат. под углом 45О
к ткани – прочность
при сдвиге
max ~ 170 МПа
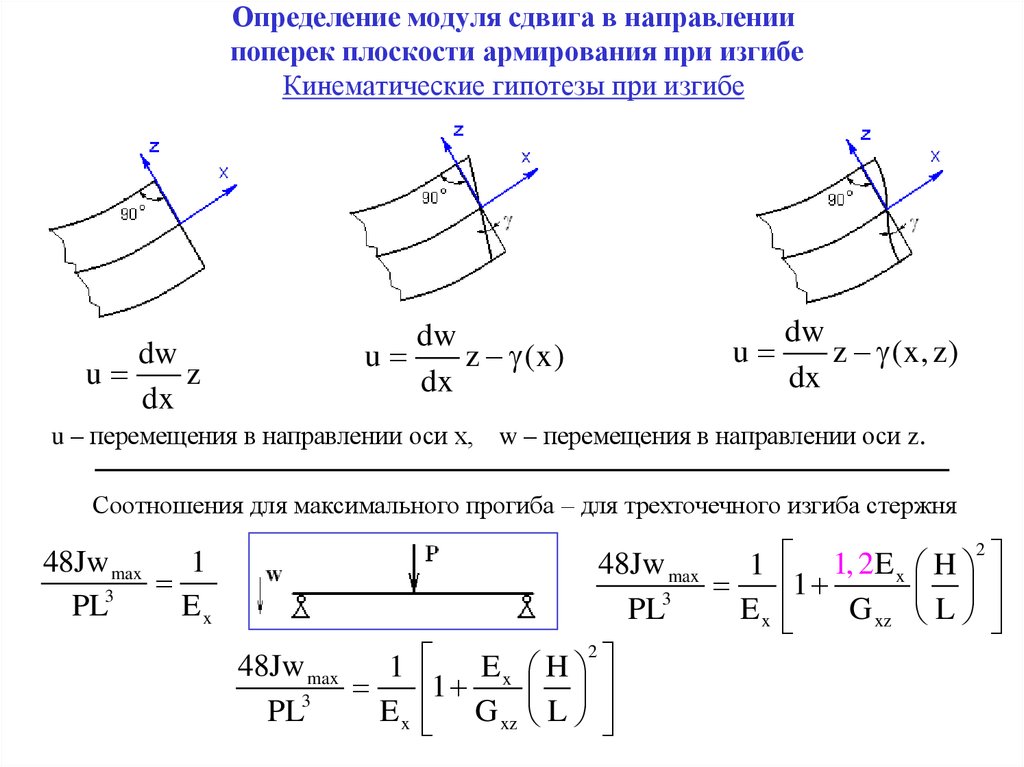
3. Определение модуля сдвига в направлении поперек плоскости армирования при изгибе Кинематические гипотезы при изгибе
dwu
z (x)
dx
dw
u
z
dx
u
dw
z (x, z)
dx
u – перемещения в направлении оси х, w – перемещения в направлении оси z.
Соотношения для максимального прогиба – для трехточечного изгиба стержня
48Jw max
1
PL3
Ex
48Jw max
PL3
48Jw max
1 1, 2E x
1
3
PL
E x
G xz
2
Ex H
1
1
E x G xz L
H
L
2
4.
Пример 1. Трехточечный изгиб стержняВлияние размеров стержня на точность определения модуля сдвига по прогибу
P
L/2
L/2
Н
X
Z
48Jw max
PL3
№ вар.
1
2
48Jw max
PL3
1
(1 k )
Ex
3
2
1, 2E x H
1
1
E x
G xz L
L
1 Ex
1,095
H
k G xz
4
5
6
Матер. Углепл. однонапр. Углепл. квазиизотр. Стеклопл. одн.
Ex (ГПа)
170
170
55
55
57
57
Gxz(ГПа)
5
5
3,5
3,5
5,2
5,2
k
0,3
0,5
0,3
0,5
0,3
0,5
L/H
11,7
9,0
7,9
6,1
6,6
5,1
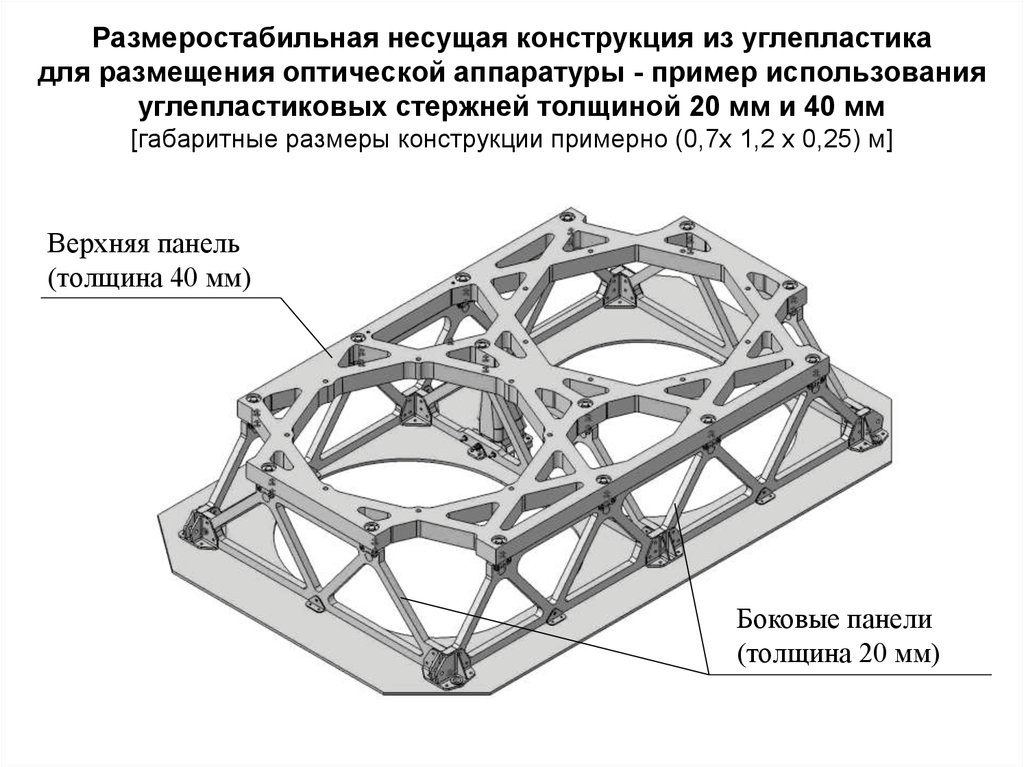
5. Размеростабильная несущая конструкция из углепластика для размещения оптической аппаратуры - пример использования
углепластиковых стержней толщиной 20 мм и 40 мм[габаритные размеры конструкции примерно (0,7х 1,2 х 0,25) м]
Верхняя панель
(толщина 40 мм)
Боковые панели
(толщина 20 мм)
6. Эксперимент – трехточечный изгиб (испытательная машина EU-40)
Типичныеэкспериментальные зависимости
прогиба от приложенной нагрузки,
измеренные двумя измерителями
перемещений
7. Экспериментальные данные по определению прогибов при поперечном изгибе
T1 M/K
K Ex
G xz
Каждая точка – результат
линейной аппроксимации
P(w) T
T
K
J x w L / 2 d
P / 2 L / 2
3
1
1
1 t и2 1 t 3и
2
6
H
M
1 t и
12 L / 2
2
L/2 d
tи
L/2
8. Вид образцов высотой 40 мм из углепластика для испытаний на трехточечный изгиб
9. Вид образцов высотой 25 мм из углерод-углеродного КМ при испытаниях на трехточечный изгиб
Перед началом нагружения,испытательная машина Instron-8801
Измерение деформаций с помощью
тензорозетки (2 датчика под углами
±45 к оси ортотропии).
Характер разрушения – в зоне
максимальных касательных
напряжений.
10. Расчеты методом конечных элементов (трехмерная модель)
При расчете использовано 25280 элементов, размер элемента 0.5х0.5х0.5 мм.Еz = 9,6 ГПа, Еy = Еx = 60 ГПа, Gxy = 20 ГПа, Gxz = Gyz = 4,6 ГПа.
Величина приложенной нагрузки – 10 кН (разрушающая нагрузка 24 кН),
размеры стержня L = 300 мм, H = 40 мм.
Сжимающие напряжения в направлении оси z
~0
( z)max = 170 МПа (F-z 550 МПа)
11.
Расчет 1/2 образца в плоскости X0ZДеформации сдвига (L = 300 мм, H = 40 мм),
макс. деф. в сечении А-А: 0,127%
Деформации сдвига (L = 150 мм, H = 40 мм),
макс. деф. в сечении А-А: 0,148%
А
А
А
А
Изгибные деформации
(L = 300 мм, H = 40 мм),
макс. деф. под опорой -0,44%
Изгибные деформации
(L = 150 мм, H = 40 мм),
макс. деф. опорой -0,24%
~0
~0
Распределение изгибных деформаций
немного несимметрично относительно
нейтральной плоскости
12.
Пример диаграмм деформирования (углепластик),построенных по показаниям датчиков,
расположенных под углами 45О к осям ортотропии образца
Результаты определения модуля поперечного сдвига по прогибу желательно
использовать только для сравнительных оценок этой характеристики при
использовании одинаково изготовленных образцов и одинаковых методик
испытаний; чем меньше диаметр опор, тем больше концентрация деформаций
и напряжений вблизи опор;
для увеличения надежности полученных результатов необходимо испытать
стержни с двумя – тремя значениями отношения высоты к длине стержня.
13. Вопросы для самоконтроля
Роль гипотез в инженерном эксперименте1. Каковы основные причины несовпадения данных расчета и эксперимента
для какого-либо объекта?
2. Сформулируйте принцип Сен-Венана.
3. От каких характеристик материала зависит область возмущения напряжений
в соответствии с принципом Сен-Венана?
Определение характеристик поперек плоскости армирования
1. Каковы основные трудности при определении характеристик упругости и прочности
поперек плоскости армирования?
2. Какие образцы можно испытывать, чтобы дать оценку характеристик сдвига поперек
плоскости армирования?
3. Какие кинематические гипотезы могут использоваться при оценке испытаний образцов
на трехточечный изгиб?
4. Каким должно быть отношение длины к высоте стержня при определении модуля
поперечного сдвига по прогибу при испытаниях на трехточечный изгиб?
5. Почему при определении модуля поперечного сдвига по прогибу при трехточечном изгибе
желательно испытывать стержни с различным отношением длины к высоте?
6. Как можно определить модуль поперечного сдвига при трехточечном изгибе с помощью
тензодатчиков? В чем преимущества этого метода?
7. Сколько тензодатчиков надо приклеить на образце при определении модуля
поперечного сдвига при трехточечном изгибе?
14. Идентификация характеристик упругости однонаправленного слоя (монослоя) по характеристикам пакетов
Прямая задачаХарактеристики
пакетов
Характеристики
слоев
Обратная задача (идентификация)
Идентификация характеристик слоя – определение таких характеристик
слоя, которые обеспечивают наилучшее соответствие экспериментальных и
расчетных значений характеристик всех рассматриваемых
сложных структур
Особенности рассматриваемых обратных задач:
- математическая формулировка – задача оптимизации;
- неединственность решения (зависит от вида функции цели);
- при идентификации характеристик монослоя – количество
заданных характеристик больше, чем количество искомых
(переопределенная задача);
- результаты решения задачи идентификации зависят от типа
характеристик пакетов, используемых в качестве исходных данных.
15. Идентификация элементов матрицы жесткости монослоя (плоское напряженное состояние)
EyE x yx
Ex
g xx
, g yy
, g xy
, g tt G xy
1 xy yx
1 xy yx
1 xy yx
N
g xx h i ci4g11 si4g 22 2si2ci2 (g12 2g 66 ) , si sin i , ci cos i
i 1
N
g yy h i si4 g11 ci4g 22 2si2ci2 (g12 2g 66 ) ,
i 1
N
g xy h i (g11 g 22 4g 66 )si2ci2 g12 (si4 ci4 ) ,
i 1
N
g tt h i (g11 g 22 2g12 )si2ci2 g 66 (si2 ci2 ) 2 ,
i 1
Прямая задача
G A G
p
0
0
[A0] – прямоугольная матрица N x 4, элементы которой зависят
только от схем армирования испытанных образцов
16.
G 0 g11 , g 22 , g12 , g 66T
- характеристики монослоя
Базовые характеристики
G g
G g ,g
э
р
(1)э
xx
(1)р
xx
,g
(1)р
yy
(1)э
yy
,g
,g
(1)р
xy
(1)э
xy
,g
,g
(2)р
xx
(2)э
xx
,g
,g
(2)р
yy
(2)э
yy
,..., g
,...,g
(N)р
xx
(N)э
xx
,g
,g
(N)э T
yy
(N)р T
yy
- числа
- алгебр. выраж-я
Задача идентификации
Функция цели:
I g g
э
j
N
р 2
j
lim 0 при g эj g рj 0
э
р
0
при
g
g
j
j
VI
2
g
II 1
g
N
р
j
э
j
2
VII
2
17. Решение задачи идентификации:
Идентификация абсолютных невязокG A G , размерность A - Nx4
э
0
R = A A A
э
G
R
G
0
T
-1
T
Идентификация относительных невязок
G A G
э
1 Aˆ G 0
{Е}
0
T
ˆ A
ˆ
Rˆ = A
-1
ˆ
A
T
T
ˆ
G 0 R E , E 1,1,...1
Предпочтительный численный метод
вычисления матриц [R] – через сингулярное разложение
18. Идентификация технических характеристик упругости монослоя
E1E2
E1 21
g11
, g 22
, g12
, g 66 G12
1 12 21
1 12 21
1 12 21
Для ортотропного пакета:
E x g xx
g 2xy
g yy
, E y g yy
g 2xy
g xx
, xy
Прямая задача
G 0 g11 , g 22 , g12 , g 66
T
g xy
g yy
, g tt G xy
19. Задача идентификации
eII 1
e
N
Фmin
р
j
э
j
2
WII
2
w
( j)
II
1
j E 0
eэj
алгоритм нелинейной численной оптимизации,
где элементы {E0} – варьируемые параметры
Устойчивость решения задачи идентификации
к случайным отклонениям в исходных данных
G G G G
э
G
G 0
э
э
0
0
G G - хорошая устойчивость
э
э
G
G 0 -
плохая устойчивость
0
1) Большие погрешности (систематические)
экспериментального определения
характеристик пакетов (ФII )
2) Недостаточное количество исходных данных
(характеристик пакетов)
3) Неудачно выбраны схемы армирования
пакетов для эксперим. определения характ-к
20. Численный эксперимент при оценке устойчивости решения задачи идентификации характеристик слоя
21. Главные преимущества определения характеристик однонаправленного слоя с использованием идентификации
Схемы армирования, обеспечивающие наибольшую устойчивостьк случайным отклонениям в базовых характеристиках
при идентификации характеристик упругости слоя
(для каждой структуры должны быть экспериментально определены
модуль упругости и коэффициент Пуассона):
0, 20 , 40 , 50 , 70 , 90
Главные преимущества определения характеристик
однонаправленного слоя с использованием идентификации
1) Определение таких характеристик слоя, которые наилучшим
образом отражают особенности поведения слоя внутри
многослойного пакета (отражают технологию формирования пакета
с несколькими направлениями укладки волокон).
2) Определение всего комплекса характеристик слоя без использования
технически сложных испытаний (например, без испытаний плоских
образцов на сдвиг).
3) Использование всей известной (избыточной) экспериментальной
информации о композите для уточнения характеристик слоя.
22. Примеры решения задач идентификации ЭМЖ
Вар. 1 – минимизация абсолютных невязок (МАН).Базовые характеристики (углепластик) в гигапаскалях, схемы армирования ± :
gxx(0)=177, gxy(0)=2,88, gxx(± 20)=138, gxy(± 20)=20, gxx(± 50)=39,1, gxy(± 50)=41,4,
gxx(90)=9,3
G р A G 0
Обозначим: сi = cos( i ), si = sin( i ), i-номер сх. армир.:
1→ =0; 2 → =20; 4 → =50; 6 → =90,
э
4 s12 c12
2 2
4 s1 c1
4 s22 c22
2
2
4 s2 c2
2
2
4 s4 c4
2
2
4 s4 c4
2
2
4 s6 c6
4
2 2
c14
s1
2 s1 c1
s12 c12 s12 c12 s14 c14
4
2 2
c24
s2
2 s2 c2
A s22 c22 s22 c22 s24 c24
4
4
2 2
c4
s4
2 s4 c4
2 2 2 2
4
4
s4 c4 s4 c4 s4 c4
4
4
2 2
c6
s6
2
s6
c6
G R G
0
T
R A A
1
Gxy G р
177
2.88
138
Gxy 20.0
39.1
41.4
9.3
g11
g22
G
0 g12
g66
T
A
23.
Вар. 2 – минимизация относительных невязок (МОН).Базовые характеристики (углепластик) в гигапаскалях:
gxx(0)=177, gxy(0)=2,88, gxx(20)=138, gxy(20)=20, gxx(50)=39,1, gxy(50)=41,4, gxx(90)=9,3
Обозначим: сi = cos( i ), si = sin( i )
Вариант 1 (МАН) 0.712
-1
a i, j
T
T
ˆ
ˆ
ˆ
ˆ
175.739
3.453
R = A A A
aˆ i, j э
1.127
gi
9.277
2.54
T
G
v
ˆ
0
2.781
G 0 R E , E 1,1,...1
4.417
0.694
1.467
g эj g рj
vj
100% kv – коэфф. вариации kv=[0,3 8,6 16,6 9,5] 0.243
э
в числ. эксп-те (%)
gj
по 10 расчетам
Вариант 2 (МОН) 0.642
0.194
175.864
Вывод: при удачно выбранных базовых
1.224
9.304
характеристиках различия между
G
0 2.886 v 2.118
минимизацией относительн. и абсолютн.
4.453
невязок невелики, хотя для существенно
0.398
анизотропных материалов предпочтительна
1.603
минимизация относительных невязок
kv=[1,7 2,6 2,9 10,5]
0.046
24.
Вар. 3 – минимизация абсолютных невязок.Базовые характеристики (углепластик) в гигапаскалях:
gxx(0)=177, gxy(0)=2,88, gxx(20)=138, gxx(40)=65,6, gxy(40)=40,7, gxx(70)=12,2, gxy(70)=17,5;
G A G
р
4 s12 c12
2 2
4 s1 c1
4 s22 c22
2
2
4 s3 c3
2
2
4 s3 c3
2
2
4 s5 c5
4 s52 c52
4
2 2
c14
s1
2 s1 c1
s12 c12 s12 c12 s14 c14
4
2 2
c24
s2
2 s2 c2
4
2 2
A c34
s3
2 s3 c3
2 2 2 2
4
4
s3 c3 s3 c3 s3 c3
2 2 2 2
4
4
s5
c5
s5
c5
s5
c5
4
4
2 2
s5
2 s5 c5
c5
177
2.88
138
Gxy 65.6
40.7
12.2
17.5
vj
0
G 0 R G э
T
R A A
1
g11
g22
G
0 g12
g66
g эj g рj
g
э
j
100%
T
A
25.
Вар. 4 – минимизация относительных невязок.Базовые характеристики (углепластик) в гигапаскалях:
gxx(0)=177, gxy(0)=2,88, gxx(20)=138, gxx(40)=65,6, gxy(40)=40,7, gxx(70)=12,2, gxy(70)=17,5;
aˆ i, j
a i, j
g iэ
T
ˆ A
ˆ
Rˆ = A
-1
ˆ
A
T
T
ˆ
G
R
E
,
E
1,1,...1
0
vj
g эj g рj
g эj
100%
kv – коэфф. вариации
в числ. эксп-те (%)
по 10 расчетам
Вывод: при неудачно выбранных
базовых характеристиках различия
между минимизацией относительных и
абсолютных невязок велики и результат
может быть грубо ошибочным
(отрицательные значения
характеристик жесткости)
0.937
Вариант 3 (МАН)
147.165
175.341
0.573
15.753
2.789
v
G
0 1.358
0.209
5.174
35.437
1.458
kv=[3,3 27,1 102 35,5]
4.584
Вариант 4 (МОН)
2.736
168.885
1.117
7.944
G
v 4.059
0 2.801
25.399
10.417
19.204
kv=[4,9 137 82 25,8] 1.458
26. Вопросы для самоконтроля
Идентификация характеристик упругости1. Какая задача является прямой, а какая обратной при определении характеристик
упругости многослойного пакета?
2. Какие величины являются исходными данными при идентификации характеристик
упругости слоя многослойного пакета?
3. Как формируется функция цели при решенении задачи идентификации характеристик
упругости слоя?
4. Что такое – абсолютные невязки характеристик пакетов и что такое
относительные невязки характеристик пакетов?
5. Для каких материалов минимизация относительных невязок при определении
элементов матриц жесткости предпочтительна и почему?
6. Чем отличается идентификация элементов матрицы жесткости слоя от идентификации
технических постоянных слоя?
7. Какая матрица называется сингулярной?
8. Почему важно знать устойчивость решения задачи идентификации
к случайным отклонениям в исходных данных?
9. Сравнение каких величин в численном эксперименте позволяет судить о хорошей или
плохой устойчивости решения задачи идентификации к случайным отклонениям
в исходных данных?
10. Что надо сделать, если устойчивость определения какой-то характеристики слоя
к случайным отклонениям в исходных данных плохая?
11. Каковы главные преимущества определения характеристик слоя с использованием
метода идентификации?
27. Задания для самостоятельного решения задачи идентификации ЭМЖ (ГПа), вар. 1, 3, 5, 7, 9, 11, 13, 15, 17 –мин. абс. невязок,
остальн – мин. отн. невязокВар. 1, 2:
gxx(0)=177, gxy(0)=2,88, gxx(20)=138, gxy(20)=20, gxx(50)=39,1, gxy(50)=41,4, gxx(90)=9,3;
Вар. 3, 4:
gxx(0)=175, gxy(0)=2,78, gxx(20)=135, gxx(40)=65,6, gxy(40)=40,7, gxx(70)=12,2, gxy(70)=17,5;
Вар. 5, 6:
gxx(0)=177, gxy(0)=2,88, gxx(20)=138, gxy(20)=20, gxx(40)=65,6, gxy(40)=40,7, gxx(90)=9,3;
Вар. 7, 8:
gxx(0)=175, gxy(0)=2,78, gxx(20)=135, gxx(50)=38,1, gxy(50)=41,4, gxx(90)=9,3;
Вар. 9, 10:
gxx(0)=177, gxx(20)=138, gxy(20)=20, gxx(50)=39,1, gxy(50)=41,4, gxx(70)=12,2;
Вар. 11, 12:
gxx(20)=138, gxy(20)=20, gxx(50)=39,1, gxy(50)=41,4, gxx(40)=65,6, gxx(70)=12,2, gxy(70)=17,5;
Вар. 13, 14:
gxx(20)=138, gxy(20)=20, gxx(40)=65,6, gxy(40)=40,7, gxx(70)=12,2, gxy(70)=17,5, gxx(90)=9,3;
Вар. 15, 16:
gxx(0)=175, gxx(20)=135, gxy(20)=20, gxx(40)=65,6, gxx(50)=38,1, gxx(70)=12,2, gxy(70)=17,5,;
28. Задания для самостоятельного решения задачи идентификации ЭМЖ (ГПа), вар. 1, 3, 5, 7, 9, 11, 13, 15, 17 –мин. абс. невязок,
остальн – мин. отн. невязокВар. 17, 18:
gxx(0)=175, gxy(0)=2,88, gxx(20)=135, gxx(40)=65,6, gxx(70)=12,2, gxч(90)=9,3,;
Вар. 19, 20:
gxx(0)=175, gxx(20)=135, gxy(20)=20, gxx(40)=65,6, gxx(50)=38,1, gxч(90)=9,3,;


























 Construction
Construction








