Признак перпендикулярности прямой и плоскости

1.

Признак перпендикулярности прямой и плоскости.
Если прямая перпендикулярна двум пересекающимся
прямым лежащим в плоскости, то она перпендикулярна к
этой плоскости.

2.

Теорема.
Если одна из двух параллельных прямых перпендикулярна
к плоскости, то и другая прямая перпендикулярна к этой
плоскости.

3.

Обратная теорема.
Если две прямые перпендикулярны к плоскости, то они
параллельны.

4.

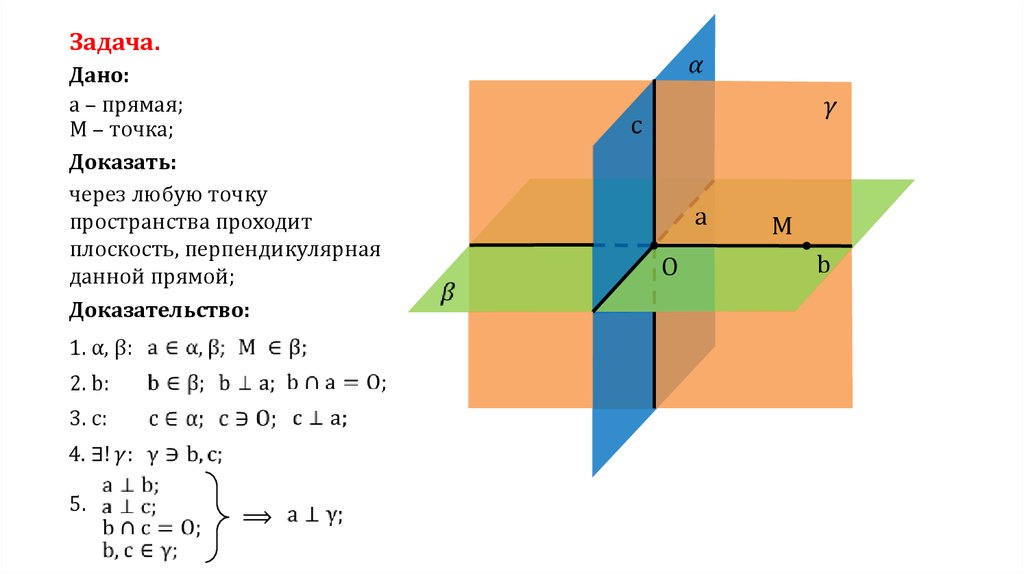
Задача.
Дано:
a – прямая;
M – точка;
Доказать:
через любую точку
пространства проходит
плоскость, перпендикулярная
данной прямой;
Доказательство:
1. α, β:
a
M

5.

Задача.
Дано:
a – прямая;
M – точка;
Доказать:
через любую точку
пространства проходит
плоскость, перпендикулярная
данной прямой;
Доказательство:
1. α, β:
2. b:
3. c:
c
a
O
M
b

6.

Задача.
Дано:
a – прямая;
M – точка;
Доказать:
через любую точку
пространства проходит
плоскость, перпендикулярная
данной прямой;
Доказательство:
1. α, β:
2. b:
3. c:
5.
⟹
c
a
O
M
b

7.

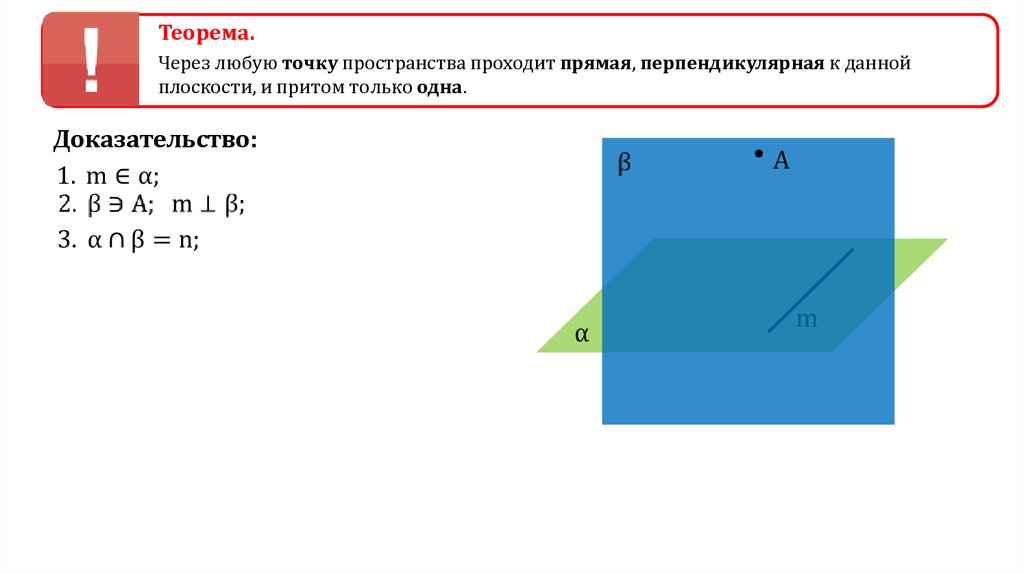
Теорема.
Через любую точку пространства проходит прямая,
перпендикулярная к данной плоскости, и притом только
одна.

8.

Теорема.
Через любую точку пространства проходит прямая, перпендикулярная к данной
плоскости, и притом только одна.
Доказательство:
A
m

9.

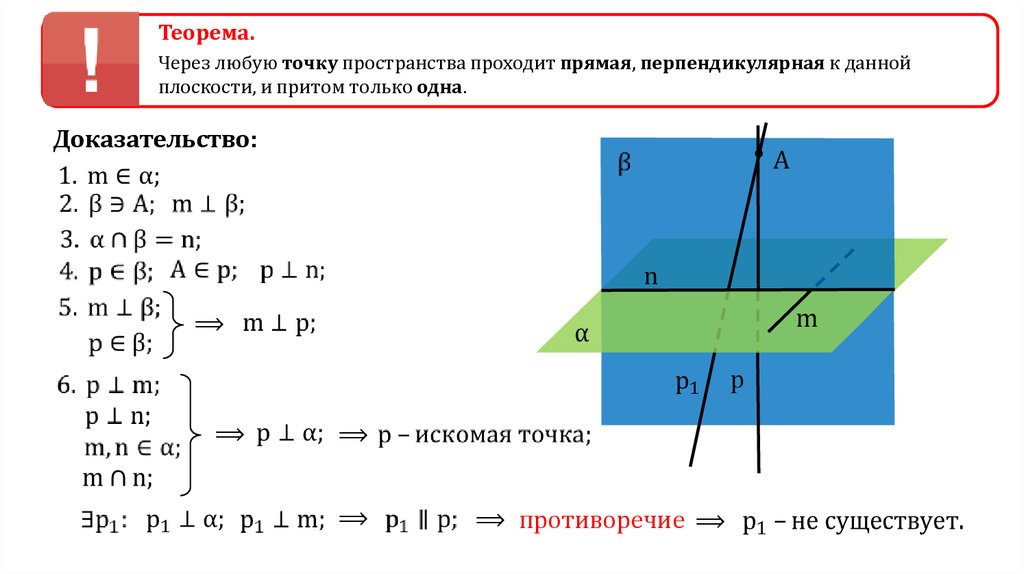
Теорема.
Через любую точку пространства проходит прямая, перпендикулярная к данной
плоскости, и притом только одна.
Доказательство:
A
n
m
⟹
p
⟹
⟹
⟹
⟹ противоречие ⟹

10.

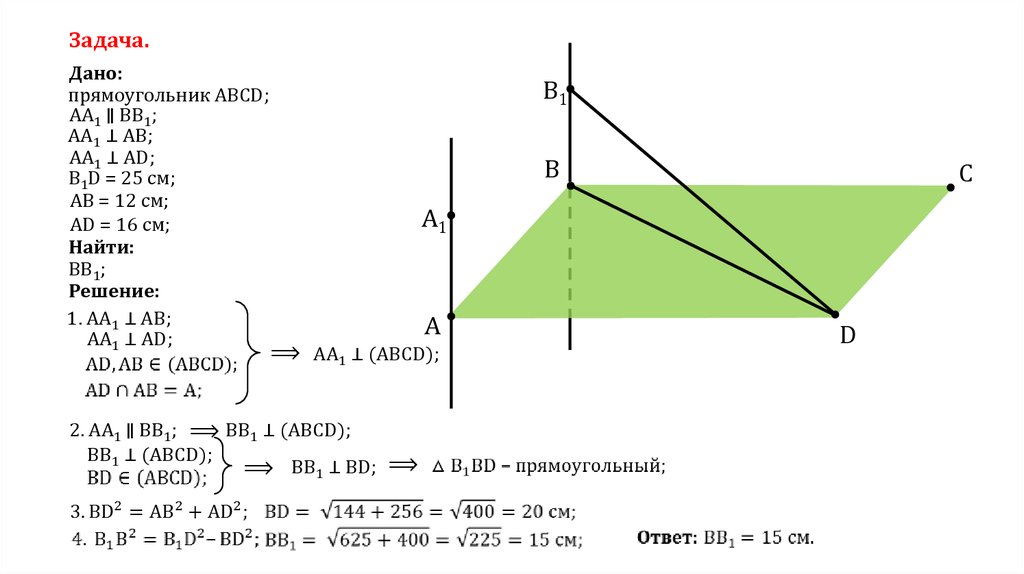
Задача.
Дано:
прямоугольник АВСD;
АА1 ∥ ВВ1;
АА1 ⊥ AB;
АА1 ⊥ AD;
В1D = 25 см;
АВ = 12 см;
AD = 16 см;
Найти:
ВВ1;
Решение:
1. АА1 ⊥ AB;
АА1 ⊥ AD;
В1
B
C
A1
A
⟹
АА1 ⊥ (ABCD);
2. АА1 ∥ ВВ1; ⟹ BB1 ⊥ (ABCD);
BB1 ⊥ (ABCD);
⟹ BB1 ⊥ BD;
⟹
D

11.

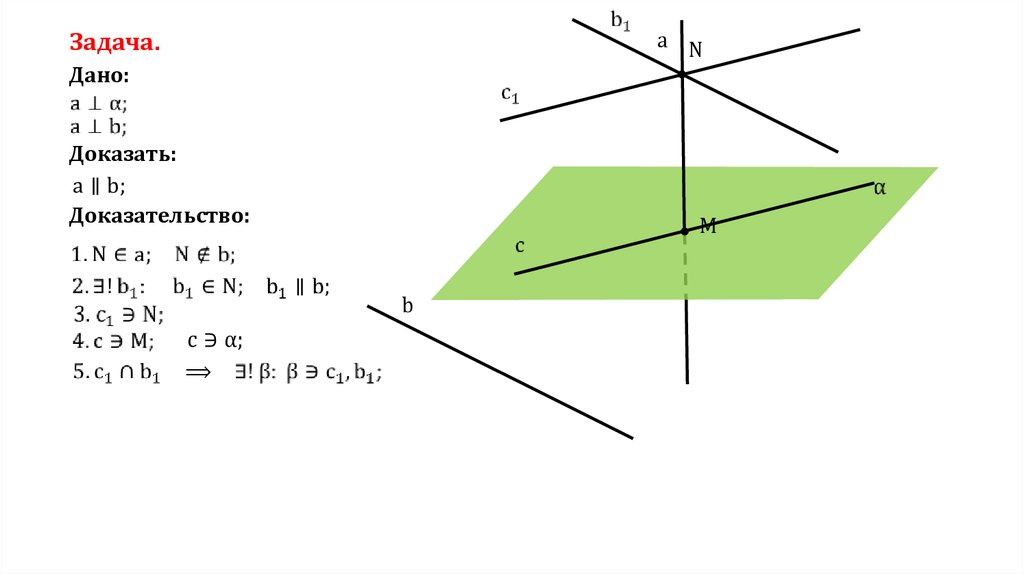
Задача.
a N
Дано:
Доказать:
Доказательство:
M
b
⟹

12.

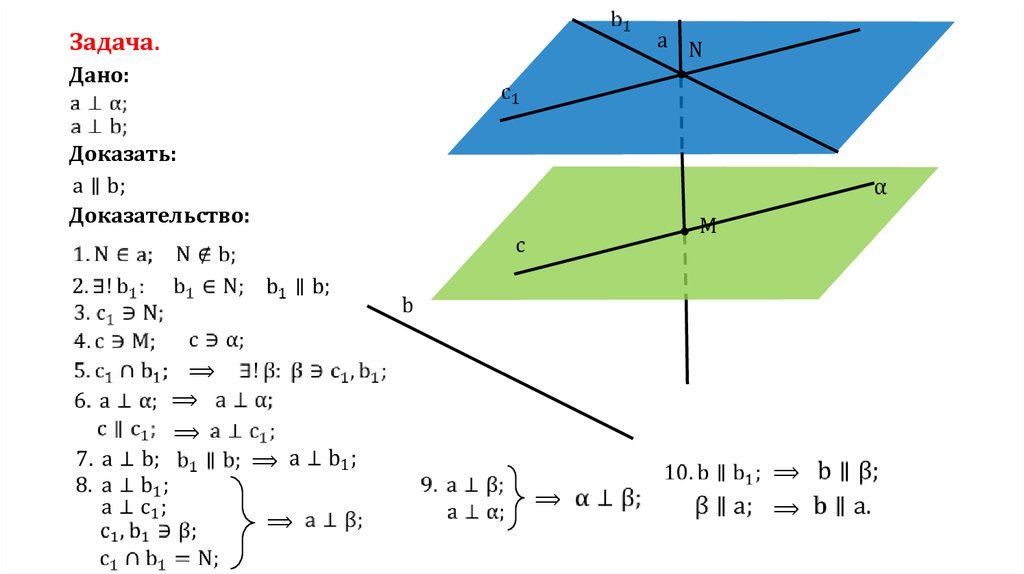
Задача.
a N
Дано:
Доказать:
Доказательство:
M
b
⟹
⟹
⟹
⟹
⟹
⟹
⟹
⟹