Pārejas procesi maiņstrāvas piedziņā

1.

PĀREJAS PROCESI
MAIŅSTRĀVAS PIEDZIŅĀ

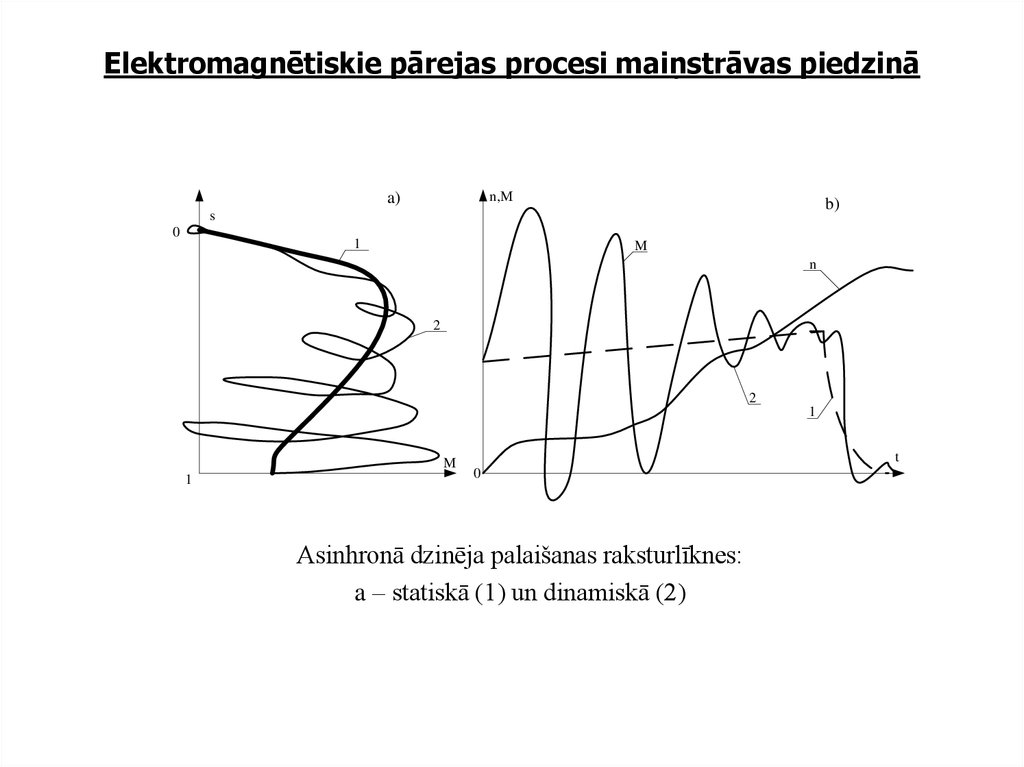
2. Elektromagnētiskie pārejas procesi maiņstrāvas piedziņā

n,M
a)
b)
s
0
1
M
n
2
2
1
M
1
t
0
Asinhronā dzinēja palaišanas raksturlīknes:
a – statiskā (1) un dinamiskā (2)

3. Trīsfāzu asinhronās piedziņas palaišana

2M k
GD 2 dn
s sk
375 dt
sk
s
dn
ds
n0
dt
dt
GD 2 ds
n0
sK
s
375 dt
s
sK
2M K
Tm s K
s
dt ( )ds,
2 s
sk
GD 2 n0
Tm
375M K

4.

Integrējot, iegūst dzinēja palaišanas laiku tukšgaitā
T
t p0 m
2
Ssāk
Sbeigu
(
SK S
)ds.
S SK
Ja palaiž dzinēju no miera, stāvokļa (ssāk = 1), tad
t p0
Tm 1 s 2
1
(
s K ln )
2 2s K
s
Par beigu slīdi praktiski pieņem s = 0,05.
Pie noteiktas sk vērtības ir minimāla attiecība tpo/Tm.
(
t p0
Tm
) min 1,22 , ja Sk = 0,407

5.

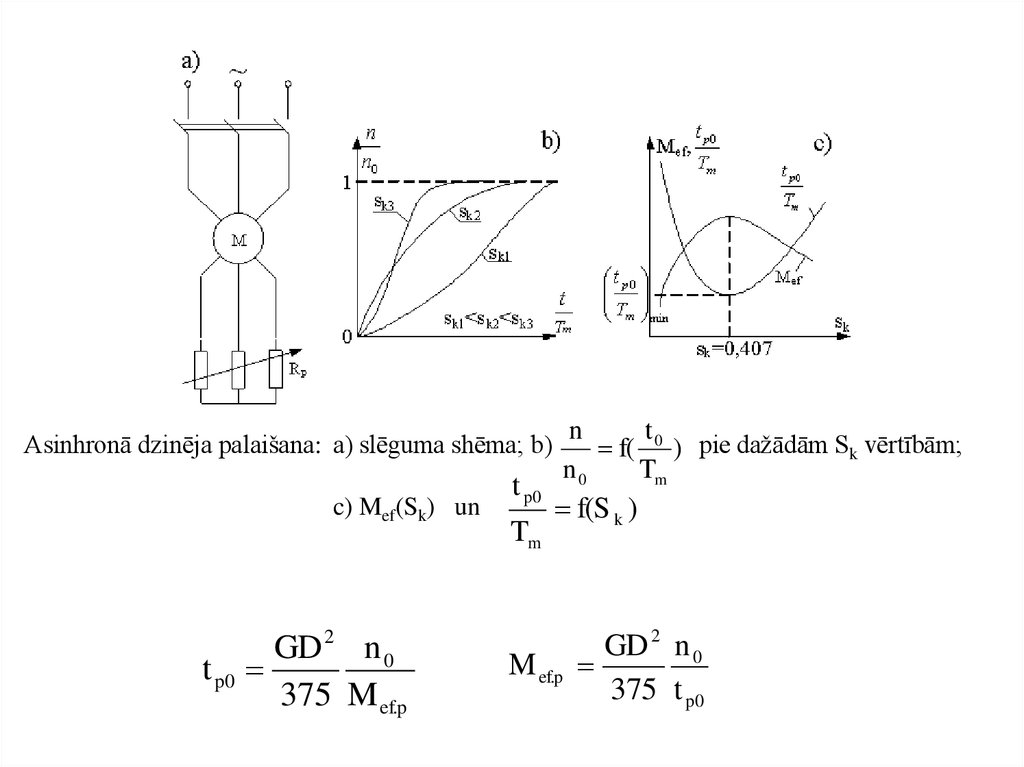
Asinhronā dzinēja palaišana: a) slēguma shēma; b)
c) Mef(Sk) un
t p0
GD 2 n 0
375 M ef.p
t p0
Tm
t
n
f( 0 ) pie dažādām Sk vērtībām;
n0
Tm
f(S k )
M ef.p
GD 2 n 0
375 t p0

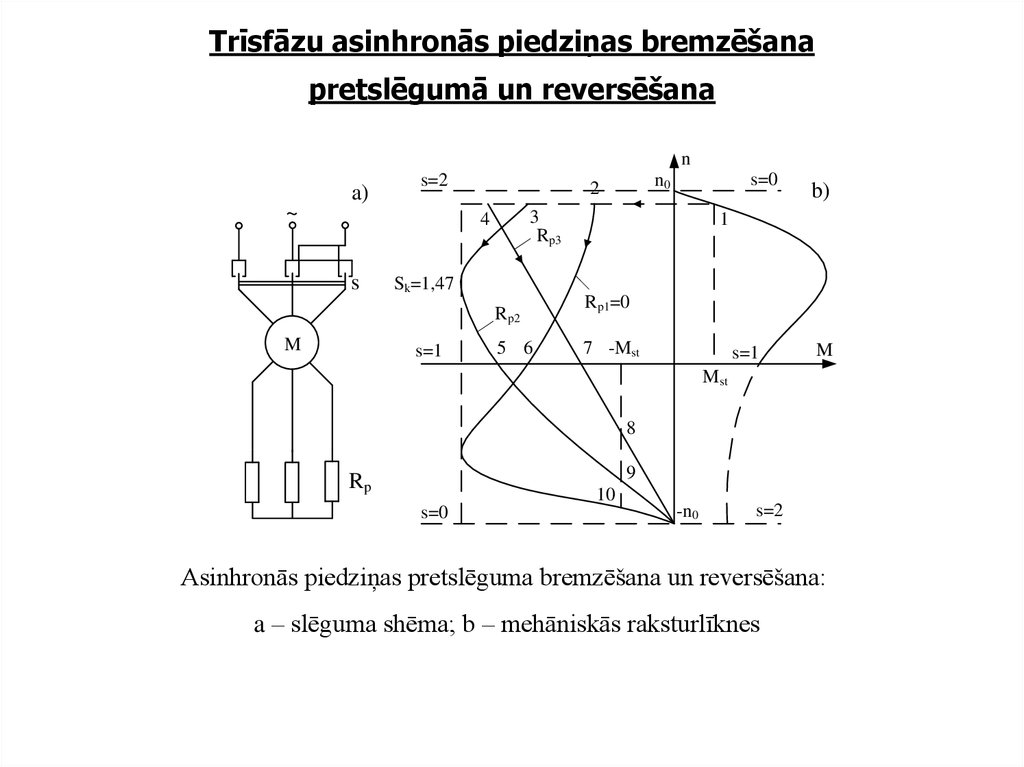
6. Trīsfāzu asinhronās piedziņas bremzēšana pretslēgumā un reversēšana

n
~
a)
s=2
2
3
Rp3
4
s
b)
1
Sk=1,47
Rp2
M
s=0
n0
s=1
5 6
Rp1=0
7 -Mst
s=1
M
Mst
8
9
Rp
10
s=0
-n0
s=2
Asinhronās piedziņas pretslēguma bremzēšana un reversēšana:
a – slēguma shēma; b – mehāniskās raksturlīknes

7.

Piedziņas pretslēguma pārejas procesu tukšgaitā (Mst=0) apraksta izteiksme:
GD 2 n 0 ds
2M K
SK S
375 dt
S SK
no Ssāk = 2 līdz Sb=1, tb0 = Tm(0,345SK+0,75/SK).
Bremzēšanas laiks ir minimāls, ja
(
t b0
) min 1,027
Tm
Efektīvo bremzēšanas momentu nosaka kā
Mef.b = MKSK/(0,75+0,345SK2)
t p.b
GD 2
n/(M ef.p.b M st )
375
pie SK = 1,47.

8. Trīsfāzu asinhronās piedziņas dinamiskā bremzēšana

a)
~
Rd.b
s
+
-
n0 n
s=1
s=0
M
RT3
RT2
RT
RT1
s=1 M
s=0
RT1<RT2<RT3
0
Mst
Asinhronā dzinēja dinamiskā bremzēšanai:
a - slēguma shēma; b - mehāniskās raksturlīknes

9.

2M max
GD 2 dn
Smax
S
375 dt
S
Smax
kur s = n/n0 - dinamiskās bremzēšanas režīma slīde;
Mmax
- maksimālais dinamiskās bremzēšanas moments;
Smax
- maksimālā dinamiskās bremzēšanas režīma slīdes vērtība
Tm
s2
t d.b.
(Smax lns
)
2
2Smax
Ja Ssāk = 1, Sbeigu = 0,05, iegūst
kur
GD 2 n0
Tm
375M max
Ssāk
Sbeigu
t d.b Tm (1,5S max
1
),
4Smax
- piedziņas elektromehāniskā konstante dinamiskās bremzēšanas režīmā.
Mef.d.b = MmaxSmax(0,25+1,5S2max).

10. Pārejas procesi trīsfāzu maiņstrāvas piedziņā ar pusvadītāju pārveidotāju

Asinhronās piedziņas palaišana ar pusvadītāju pārveidotāju:
a – slēguma shēma; b – dinamiskā raksturlīkne;
c – palaišanas diagramma pie trapecveidīga piedziņas paātrinājuma

11.

fp = kf.t ,
No 0 lIdz t1 :
pie kam
εp
dn 0 2π
kf
dt
p
ε = ρt un n = ρt2/2.
dn
t2
n nost (t) Tm
n Tmρt ρ
dt
2
No t1 līdz t2
ε = εmax, n = nsāk1 + εmaxt,
nnost(t) = nsāk1 + εmaxt + Tmεmax,
No t2 līdz t3
ε = εmax – ρt
n = nsāk2 + εmaxt – ρt2/2,
nnost(t) = nsāk2 + Tm εmax + εmaxt - Tmρt – ρt2/2,
nsāk2 = nsāk1 + εmax(t2-t1).
kur

12. Pārejas procesi trīsfāzu maiņstrāvas piedziņā ar sinhrono dzinēju

Parasti sinhronos dzinējus izmanto neregulējamās piedziņās ar ilgstošu darba režīmu
pie nemainīgas vai pulsējošas slodzes.
Sarežģīts pārejas process notiek dzinējam ievelkoties "sinhronismā”, tas ir, kad
"saķēdējas" statora un rotora magnētiskie lauki.
Sie 0,0564 M m /Jω0
kur Mm ir sinhronā dzinēja maksimālais moments.
Ir attīstījusies regulējama piedziņa ar sinhrono dzinēju un frekvenču
pārveidotāju. Ja pārveidotāja izejas sprieguma frekvences maiņa notiek ar laika
konstanti, kas lielāka par sinhronā dzinēja elektromehānisko laika konstanti, tad
pārejas procesi šādā piedziņā noris tāpat kā līdzstrāvas piedziņā ar pusvadītāju
pārveidotāju.

13.

ELEKTRISKĀS PIEDZIŅAS
ENERĢĒTIKA

14. Enerģētiskie rādītāji

Jēdziens "elektriskās piedziņas enerģētika" ietver sevī jautājumus, kas apskata elektroenerģijas
patēriņu un izmantošanu, enerģijas zudumus elektromehāniskajos un pusvadītāju pārveidotājos,
aktīvās un reaktīvās enerģijas izmantošanas efektivitāti.
Galvenie elektriskās piedziņas enerģētiskie radītāji ir:
no tīkla uzņemtā jauda P1;
no tikla uzņemtā enerģija A1;
lietderīgi izmantotā jauda P2;
lietderīgi izmantotā enerģija A2;
jaudas zudumi ΔP;
enerģijas zudumi ΔA;
lietderības koeficients η;
jaudas koeficients cosφ.

15.

Enerģijas zudumi līdzstrāvas piedziņā
P Pk Pv
Pk Pf PFe Pmeh
Pv I a2 R
kur
Pk
- pastāvīgie zudumi;
Pv
- mainīgie zudumi;
Pf
- ierosmes zudumi;
PFe
- zudumi dzelzī;
Pmeh
- mehāniskie zudumi.
Pv M ( 0 ) M 0
0
P12
0

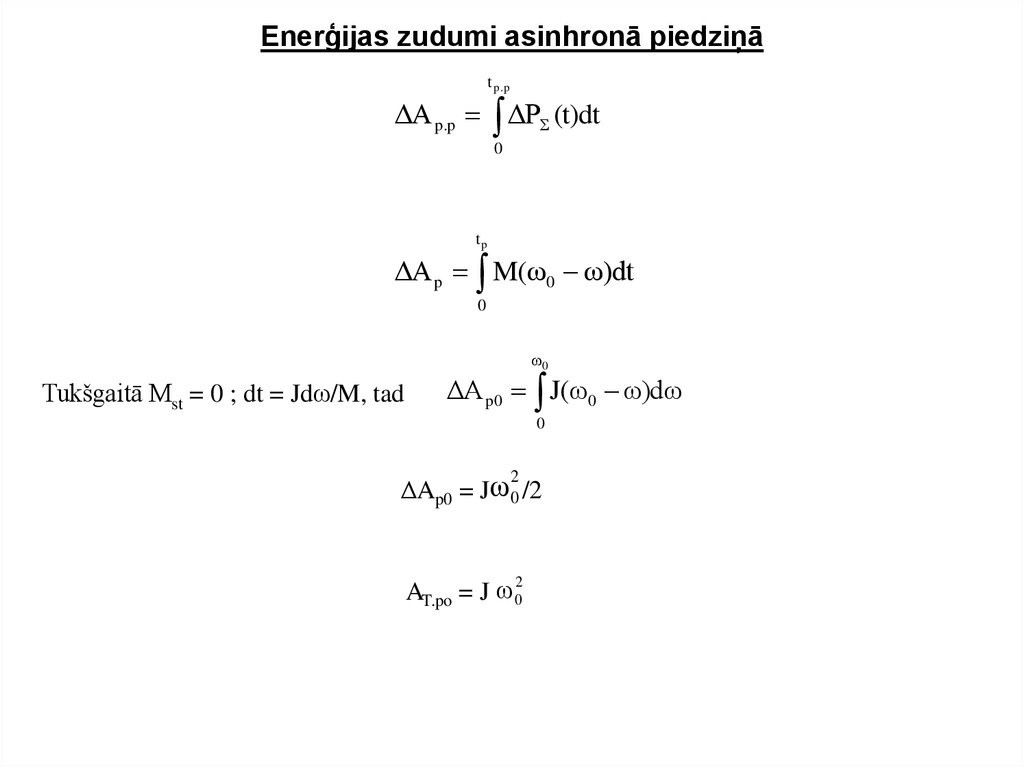
16. Enerģijas zudumi asinhronā piedziņā

t p.p
ΔA p.p ΔPΣ (t)dt
0
tp
ΔA p M(ω0 ω)dt
0
ω0
Tukšgaitā Mst = 0 ; dt = Jdω/M, tad
ΔA p0 J(ω0 ω)dω
0
ΔAp0 = Jω 0 /2
2
AT.po = J ω 0
2

17.

a)
g
P
c
ΔPk
d
ω0
b
a
P,ω
ω0
ωst
0
ω
e
ΔPk t
tp0
Ap .st
M st
ΔAp0
Ap0
b)
ω
f
0
t
tp
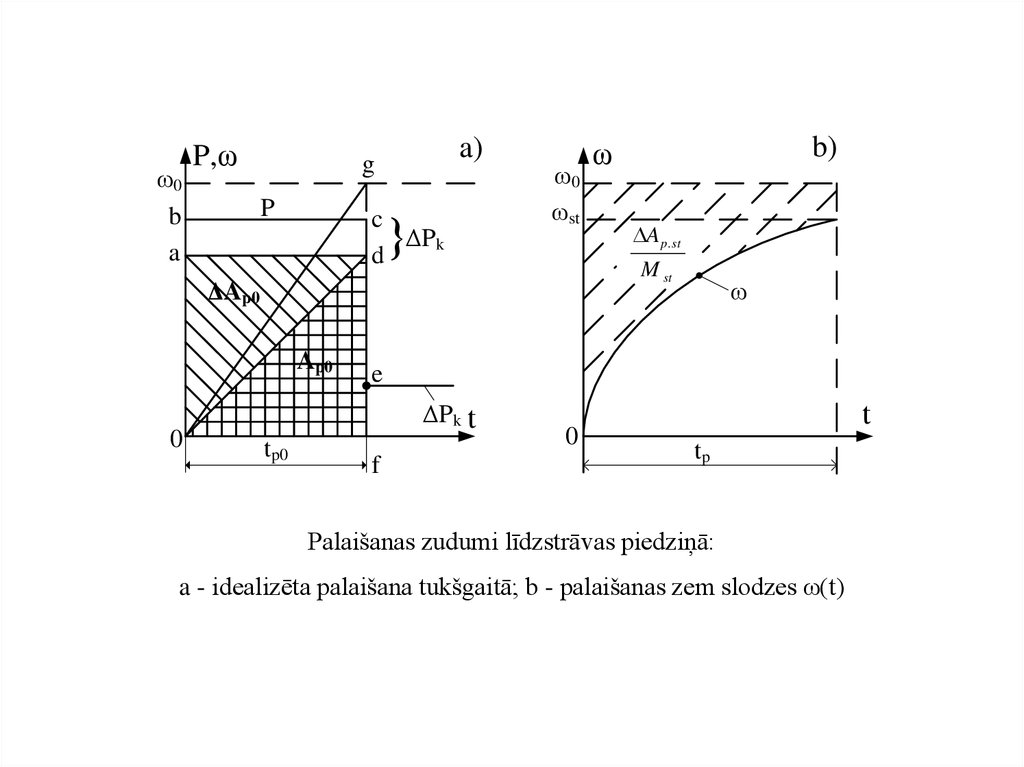
Palaišanas zudumi līdzstrāvas piedziņā:
a - idealizēta palaišana tukšgaitā; b - palaišanas zem slodzes ω(t)

18.

Palaižot dzinēju pie konstantas slodzes, enerģijas zudumi ir:
tp
tp
0
0
ΔA p M(ω0 ω)dt (M st M din )(ω0 ω)dt
Tā kā dt=Jdω/Mdin, tad
tp
ΔA p J(ω0 ωst ωst2 /2) M st (ω0 t p ωdt)
0

19.

Enerģijas zudumus līdzstrāvas piedziņā pretslēguma bremzēšanas režīmā tukšgaitā (Mst = 0):
0
ω0
ω0
0
ΔA p.br.0 J( ω0 ω)dω J(ω0 ω)dω
ΔAp.br.0 = 3·Jω02/2
Bremzējot pretslēgumā slogotu dzinēju slodzes Mst = const, enerģijas zudumi ir
t br
ΔA p.br J(ω0 ωst ωst2 /2) M st (ω0 ω)dt
0

20.

Līdzstrāvas piedziņas reversēšana tukšgaitā izsauc enerģijas zudumus
ΔA r0
ω0
J( ω0 ω)dω
ω0
ω0
ω0
Jω02
j(ω0 ω)dω 4
2
Dinamiskās bremzēšanas režīmā dzinējam tukšgaitas enerģijas zudumi ir
Ad .br 0
J 02
J d J d
2
0
0
0
0
Ja dinamiski bremzē līdzstrāvas piedziņu pie Mst = const, tad
ΔA d.br
t br
ω
J
M st ωdt
2
0
2
st

21. Enerģijas zudumi asinhronā piedziņā

ΔPV 3(I R 1 I' R' 2 )
2
1
2
2
ΔPV = Mω0s(1+R1/R’2) = P12s(1+R1/R’2)
t p.p
ΔA p.p ΔPΣ (t)dt
0

22.

Asinhronā dzinējā enerģijas zudumi palaišanas procesā tukšgaitā ir
tp
ΔA p 3I '22 (R 1 R |2 R |2p )dt
0
Pieņemot, ka Mst = 0, dt = -(Jω0/M)ds, un izsakot rotora zudumus kā
3I’2(R’2+R’2p) = Mωs, pēc pārveidošanas iegūst:
R1
2
Jω
s
1
ds
0
R' 2 R' 2p
Sbeigu
SSsāk
ΔA p
sāā
Ievērojot, ka Ssāk = 1 un Sbeigu, iegūst
ΔA p0
kur
Jω 02
R1
(1
)
2
R' 2 R' 2p
ω0
- asinhronā dzinēja sinhronais leņķiskais ātrums;
R2p
- uz statoru reducētā rotora papildpretestība.

23.

Asinhronā dzinēja palaišanas enerģijas zudumus iedala divās daļās:
1. zudumi rotorā kinētiskās enerģijas iegūšanai: ΔAp02=Jω02 /2;
2. zudumi statorā: ΔAp01=J ω02R1/2(R’2+R’2p).
Pie konstantas slodzes asinhronā dzinēja palaišanas zudumus
var aprēķināt no izteiksmes:
ΔA p A p0
kur
Mp.vid = (λ+kp)MN/2
λ = MK/MN
kp = Mp/MN
M p.vid
M p.vid M st
- asinhronā dzinēja vidējais palaišanas moments.

24.

Pretslēguma bremzēšanas režīmu aprēķinos ievieto integrēšanas robežas
Ssāk = 2 un Sbeigu = 1. Tad enerģijas zudumi ir
ΔA p.b0
3Jω 02
R1
(1
)
2
R' 2 R' 2p
Zudumi asinhronā piedziņā pretslēguma bremzēšanas režīmā pie slodzes
Mst = const ir:
ΔA p.b. ΔA p.b0
M b.vid
M b.vid M st
kur
Mb.vid
- asinhronā dzinēja vidējais moments pretstrāvas
bremzēšanas režīmā

25.

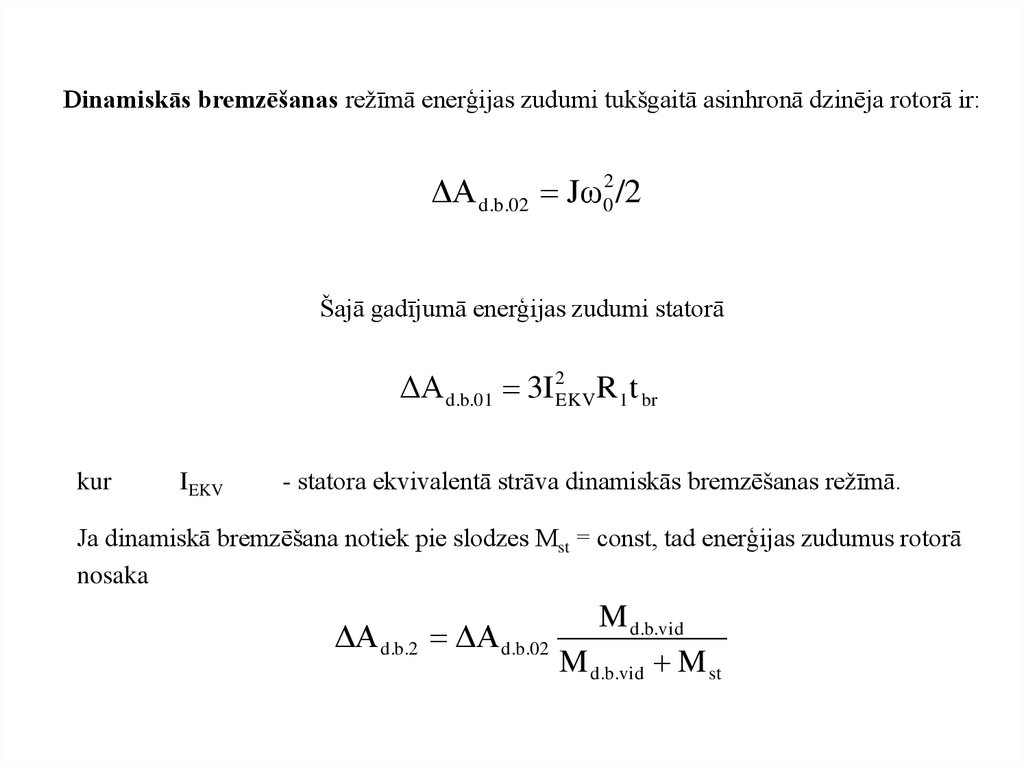
Dinamiskās bremzēšanas režīmā enerģijas zudumi tukšgaitā asinhronā dzinēja rotorā ir:
ΔA d.b.02 Jω02 /2
Šajā gadījumā enerģijas zudumi statorā
ΔA d.b.01 3I 2EKVR 1t br
kur
IEKV
- statora ekvivalentā strāva dinamiskās bremzēšanas režīmā.
Ja dinamiskā bremzēšana notiek pie slodzes Mst = const, tad enerģijas zudumus rotorā
nosaka
ΔA d.b.2 ΔA d.b.02
M d.b.vid
M d.b.vid M st