Similar presentations:
Elektriskās piedziņas pārejas procesi. (№4)
1.
ELEKTRISKĀS PIEDZIŅASPĀREJAS PROCESI
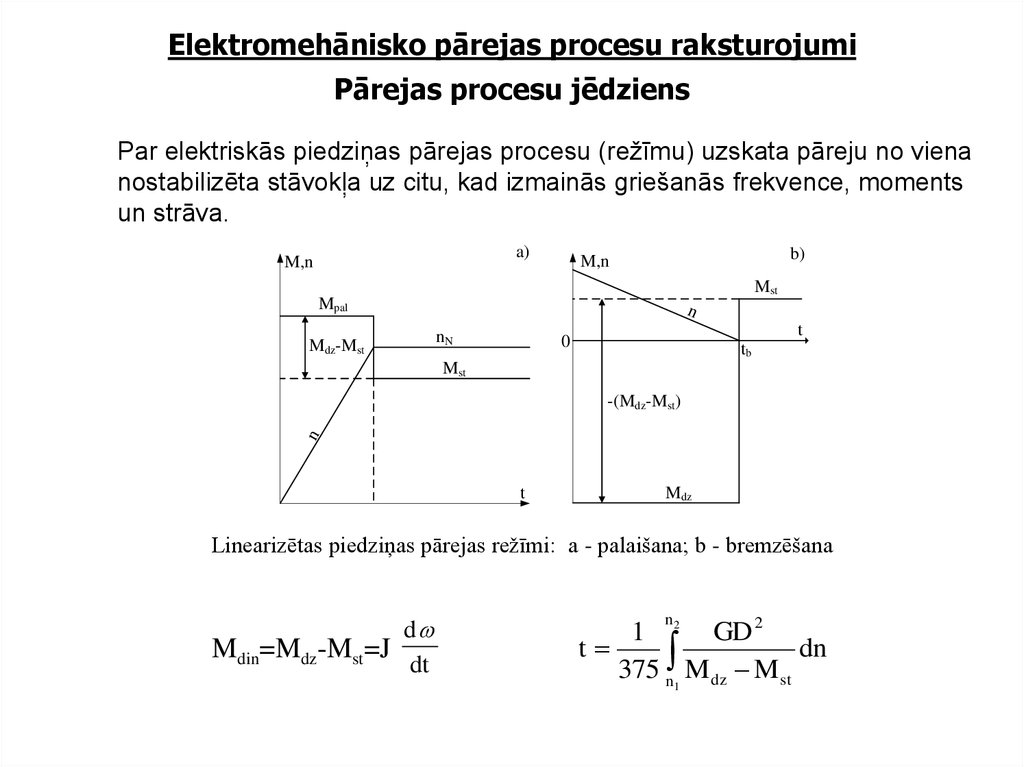
2. Elektromehānisko pārejas procesu raksturojumi Pārejas procesu jēdziens
Par elektriskās piedziņas pārejas procesu (režīmu) uzskata pāreju no vienanostabilizēta stāvokļa uz citu, kad izmainās griešanās frekvence, moments
un strāva.
a)
M,n
b)
M,n
Mst
Mpal
Mdz-Mst
n
nN
t
0
tb
Mst
n
-(Mdz-Mst)
t
Mdz
Linearizētas piedziņas pārejas režīmi: a - palaišana; b - bremzēšana
d
Mdin=Mdz-Mst=J
dt
n
1 2 GD 2
t
dn
375 n1 M dz M st
3. Linearizētas elektriskās piedziņas mehānisko pārejas procesu analītiskais aprēķins
GD 2Σ dn,
M din M dz M st
375 dt
M dz M K βn,
M M β n,
st0
st
st
kur Mk un Mst0 - dzinēja un mehānisma momenti pie nulles ātruma;
β un βst
- attiecīgo mehānisko raksturlīkņu cietības moduļi.
4.
GD 2Σ dn(β β st )n M K M st0
375 dt
dn
Tm
n n nost ,
dt
kur
GD 2Σ
Tm
375(β β st )
- elektriskās piedziņas mehāniskā laika
konstante;
M K M st0
β β st
- nostabilizējusies griešanās frekvence.
n nost
5.
n nnost Cet
Tm
,
kur C - integrēšanas konstante.
Pie sākuma nosacījumiem, ja n=nsāk t=0, integrēšanas konstante C = nsāk - nnost.
Ievietojot C vērtību
n nnost (nsāk nnost )e
M Mnost (Msāk Mnost )e
t
Tm
t
Tm
6.
Linearizētas piedziņas griešanās frekvencesizmaiņas grafiks, ja Mst = const
7. Piedziņas pārejas procesu aprēķins ar grafisko integrēšanu
M dz M st Δω,
J
Δt
vai
M dz M st Δn
2
GD /375 Δt
8.
nMdz
Mst
6
C3
9
8
7
C2
Mdz-Mst
C1
4
5
n=f(t)
3
B2
B1
B
2
C
B3
t
1 A
0
D
D1
D2
D3
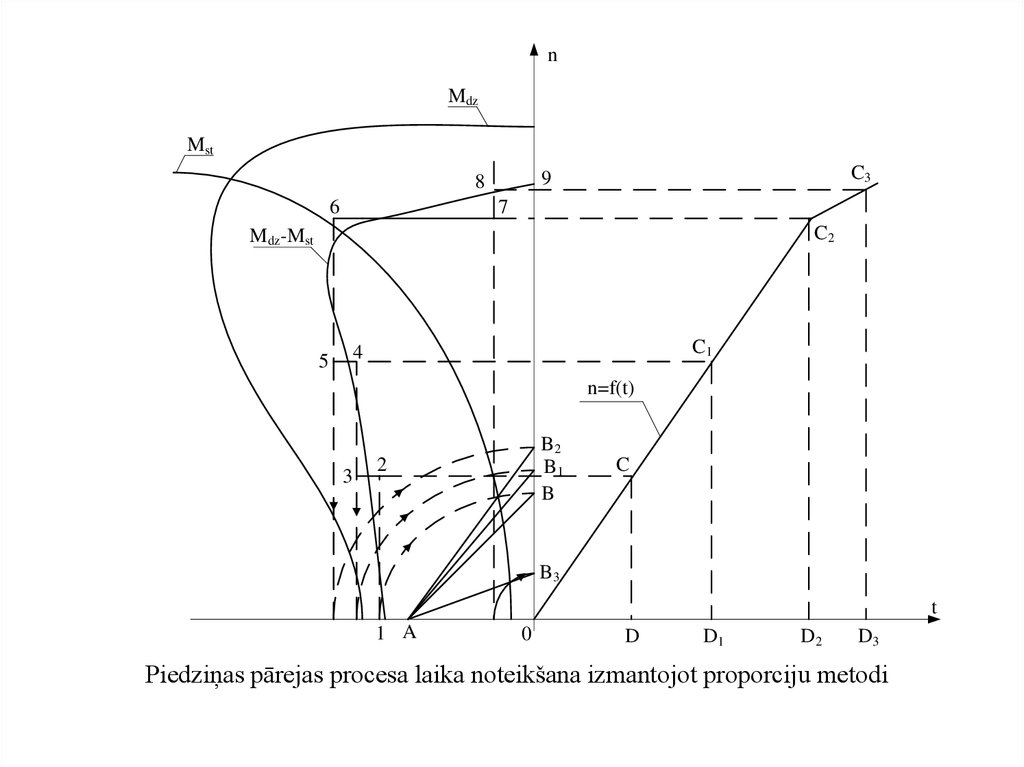
Piedziņas pārejas procesa laika noteikšana izmantojot proporciju metodi
9.
PĀREJAS PROCESILĪDZSTRĀVAS PIEDZIŅĀ
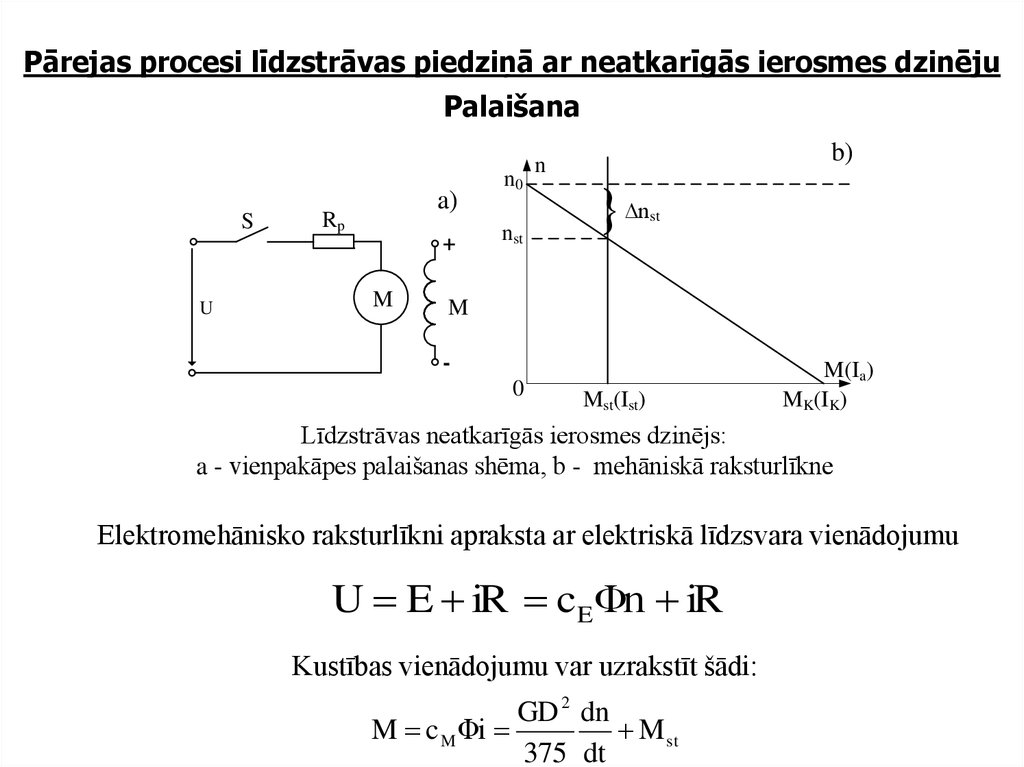
10. Pārejas procesi līdzstrāvas piedziņā ar neatkarīgās ierosmes dzinēju Palaišana
Rp+
U
M
nst
S
a)
n0
b)
n
∆nst
M
0
Mst(Ist)
M(Ia)
MK(IK)
Līdzstrāvas neatkarīgās ierosmes dzinējs:
a - vienpakāpes palaišanas shēma, b - mehāniskā raksturlīkne
Elektromehānisko raksturlīkni apraksta ar elektriskā līdzsvara vienādojumu
U E iR cE Φn iR
Kustības vienādojumu var uzrakstīt šādi:
GD 2 dn
M c M Φi
M st
375 dt
11.
M st RU
GD 2
R
dn
n
;
2
2
cEΦ
375 c E c M Φ dt c E c M Φ
n 0 n Tm
kur
n0 = U/cEΦ
GD 2
R
Tm
375 c E c M Φ 2
Δnst = MstR/cEcMΦ2
dn
Δn st ,
dt
- ideālās tukšgaitas griešanās frekvence;
- mehāniskā laika konstante;
- griešanās frekvences lieluma izmaiņas
pretestības momenta Mst iedarbības rezultātā.
n n st (1 e
t
Tm
)
12.
Līdzstrāvas neatkarīgās ierosmes dzinēja vienpakāpes palaišanas raksturlīknes:a - n(t); b - i(t); 1 - ar slodzi , 2 - tukšgaitā
n n 0 (1 e
t
Tm
)
t
Tm
i Ist (I K Ist )e ,
13. Palaišana ar daudzpakāpju reostatu
++
M
-
a)
K1
Rp1
Rp2
K2
K3
-
M
Ra
Ip1
n
Ip2
Ist
b)
n0
c)
i,n
i
Tm2
Tm1
Tm3
nst3
nst2
nst1
n
Ia
Ist Ip2
Ip1
t1
t2
tp
3Tms
t3
t
Līdzstrāvas neatkarīgās ierosmes dzinēja daudzpakāpju palaišana ar reostatiem:
a -slēguma shēma; b - elektromehāniskās raksturlīknes; c - n(t) un i(t)
14.
Laiku, kurā dzinēja enkura strāva izmainās no Ip1 līdz Ip2, nosaka pēc izteiksmes:I p2 I st (I p1 I st )e
kur
tx
Tmx
tx
Tmx
,
- dzinēja palaišanas laiks attiecīgajā pakāpē;
- attiecīgās reostata palaišanas pakāpes mehāniskā laika konstante,
kas atkarīga no enkura ķēdes kopējās aktīvās pretestības.
tx = Tmxln
I p1 I st
I p2 I st
Katrai nākošai palaišanas pakāpei laiks samazinās t1 > t2 > t3. Pēdējās
pakāpes laiku (Rp = 0 un Isāk = Ipr) nosaka pēc empīriskas formulas
t3=~3Tm.dz.
Dzinēja palaišanā ar daudzpakāpju reostatu kopējais laiks ir
vienāds ar visu atsevišķo pakāpju laiku summu.
15. Pretslēguma bremzēšana un reversēšana
n-
+
a)
b)
n0
2
1
nst
Rp
3 -Mst
S
-Msāk -Mk1
(-Isāk) (-Ik1) 4
-nst1
-n0
-
5
-nst2
n0 n
nst 2
c)
-nst1
-n0
-nst2
-Δnst
6
d)
i
1
t
0
1
Ist
M
M(Ia)
-Δnst
M
+
Mst(Ist)
t
0
3
2
-Ist
-Ik1
3
-Isāk
Līdzstrāvas neatkarīgās ierosmes dzinēja pretslēguma bremzēšanas un reversēšanas režīmi:
a - slēguma shēma; b - mehāniskās raksturlīknes; c - reversēšanas diagrammas n(t) aktīva pretestības
momenta gadījumā (1), reaktīva (3) un tukšgaitā (2); d - i(t) diagrammas reversēšanas gadījumā
16.
Aktīva pretestības momenta gadījumā nnost=-(n0 + Δnst), nsāk = nst un iegūst:n (n 0 Δn st ) (n st n 0 Δn st )e
nnost= - n0 ; nsāk = n0:
t
Tm
Isāk=(U+cEΦnsāk)/(Ra+Rp)
Reversējot tukšgaitā, iegūst
t
Tm
n n 0 2n 0 e
i Ist (Isāk Ist )e
kur
i 2I k e
t
Tm
t
Tm
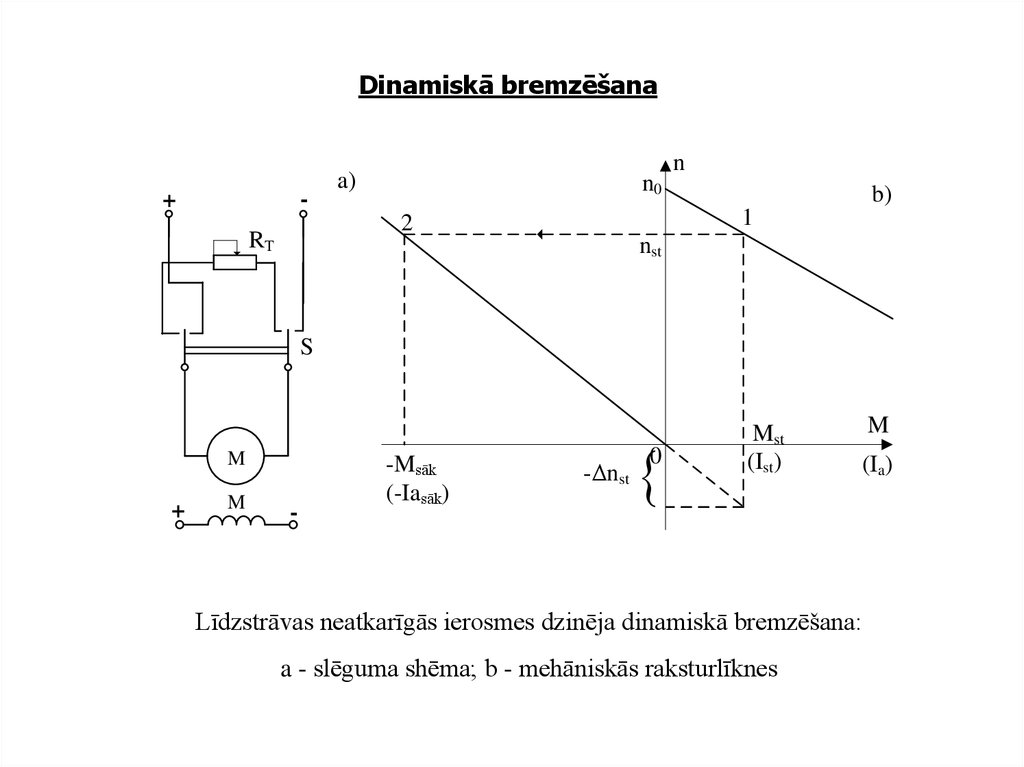
17. Dinamiskā bremzēšana
-+
a)
n0
b)
1
2
RT
n
nst
S
M
+
M
-
-Msāk
(-Iasāk)
-Δnst
0
Mst
(Ist)
M
(Ia)
Līdzstrāvas neatkarīgās ierosmes dzinēja dinamiskā bremzēšana:
a - slēguma shēma; b - mehāniskās raksturlīknes
18.
Dinamiskās bremzēšanas procesu raksturo vienādojumu sistēma:c E Φn iR 0
,
GD 2 dn
M st
c M Φi
375 dt
kur
R = Ra + RT
- enkura ķēdes aktīvā pretestība.
Ievērojot sākuma nosacījumus ja t = 0 un n = nsāk = nst aprēķina C = nsāk + Δnst,
kur Δnst=MstR/cEcMΦ2. Atrisinot un ievietojot C, iegūst izteiksmi
n Δnst (nsāk Δnst )e
t
Tm
Tukšgaitā, ja Mst=0, Δnst=0 un nsāk=n0, izteiksme vienkāršojas:
n n 0e
t
Tm
19.
ni
a)
n0
b)
nst
Ist
2
1
0
-Δnst
a
t
a
0
1
t
2
-Ia.sāk.
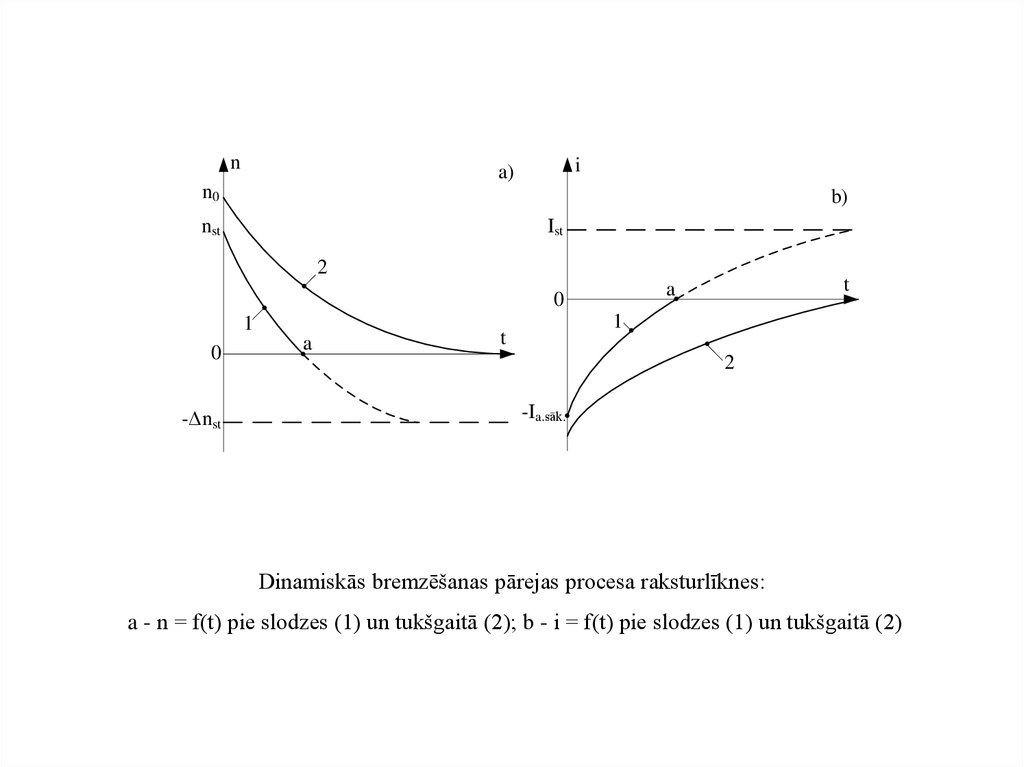
Dinamiskās bremzēšanas pārejas procesa raksturlīknes:
a - n = f(t) pie slodzes (1) un tukšgaitā (2); b - i = f(t) pie slodzes (1) un tukšgaitā (2)
20.
Dzinēja enkura strāvas izmaiņu laikā dinamiskās bremzēšanas režīmā pienorādītajiem sākuma nosacījumiem apraksta izteiksme:
i (Ia.sā. Ist )e
Bremzēšanas procesa laiks ir:
t
Tm
Ist
t1 Tm ln
n sāk Δn st
n1 Δn st
Dinamiski bremzējot konstanti slogotu dzinēju līdz tas apstājas n1 = 0, pārejas
procesa laiku nosaka pēc vienkāršotas izteiksmes:
t T Tm ln
n sāk Δn st
Δn st
Ja bremzējam dzinēju tukšgaitā pie nosacījuma, ka Ist = 0, Δnst = 0, tad pieņemts
bremzēšanas laiku noteikt kā
tT 3Tm
21. Pārejas procesi līdzstrāvas piedziņā ar pusvadītāju pārveidotāju
Līdzstrāvas piedziņas palaišana ar pusvadītāju pārveidotāju:a- slēguma shēma; b - dinamiskā raksturlīkne; c - n = f(t), M = f(t)
n ε p t Tm ε p (1 e
t
Tm
),
εp
t
U p.N
c E Φt p
GD 2
M Mst
ε p (1 e Tm ).
375
















 physics
physics




